2019-2020学年黑龙江省哈尔滨163中八年级下学期期中数学试卷(五四学制) (word,解析版)
文档属性
| 名称 | 2019-2020学年黑龙江省哈尔滨163中八年级下学期期中数学试卷(五四学制) (word,解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 06:27:25 | ||
图片预览


文档简介
2019-2020学年黑龙江省哈尔滨163中八年级第二学期期中数学试卷(五四学制)
一、选择题
1.(3分)下列各组线段中,能构成直角三角形的是( )
A.2,3,4 B.3,4,6 C.5,12,13 D.4,6,7
2.(3分)顺次连接矩形四边中点得到的四边形一定是( )
A.正方形 B.矩形 C.菱形 D.平行四边形
3.(3分)如图,已知在?ABCD中,∠A+∠C=140°,则∠B的度数是( )
A.110° B.120° C.140° D.160°
4.(3分)矩形ABCD的对角线AC、BD相交于点O,AB=4cm,∠AOB=60°,则这个矩形的对角线长是( )
A.2cm B.4cm C.6cm D.8cm
5.(3分)如图,一只蚂蚁从正方体的下底面A点沿着侧面爬到上底面B点,正方体棱长为3cm,则蚂蚁所走过的最短路径是( )
A.3cm B.6cm C.3cm D.3cm
6.(3分)如图,四边形ABCD是正方形,△CDE是等边三角形,连接AE,则∠AED的度数为( )
A.10° B.15° C.20° D.30°
7.(3分)在平面直角坐标系中,?ABCD的顶点A、B、D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )
A.(3,7) B.(5,3) C.(7,3) D.(8,2)
8.(3分)已知关于x的一次函数y=(2﹣m)x+2+m的图象上两点A(x1,y1),B(x2,y2),若x1<x2时,y1>y2,则m的取值范围是( )
A.m>2 B.m>﹣2 C.m<2 D.m<﹣2
9.(3分)如图,菱形ABCD和菱形ECGF的边长分别为4和2,∠B=120°,则图中阴影部分的面积是( )
A.3 B.2 C.4 D.3
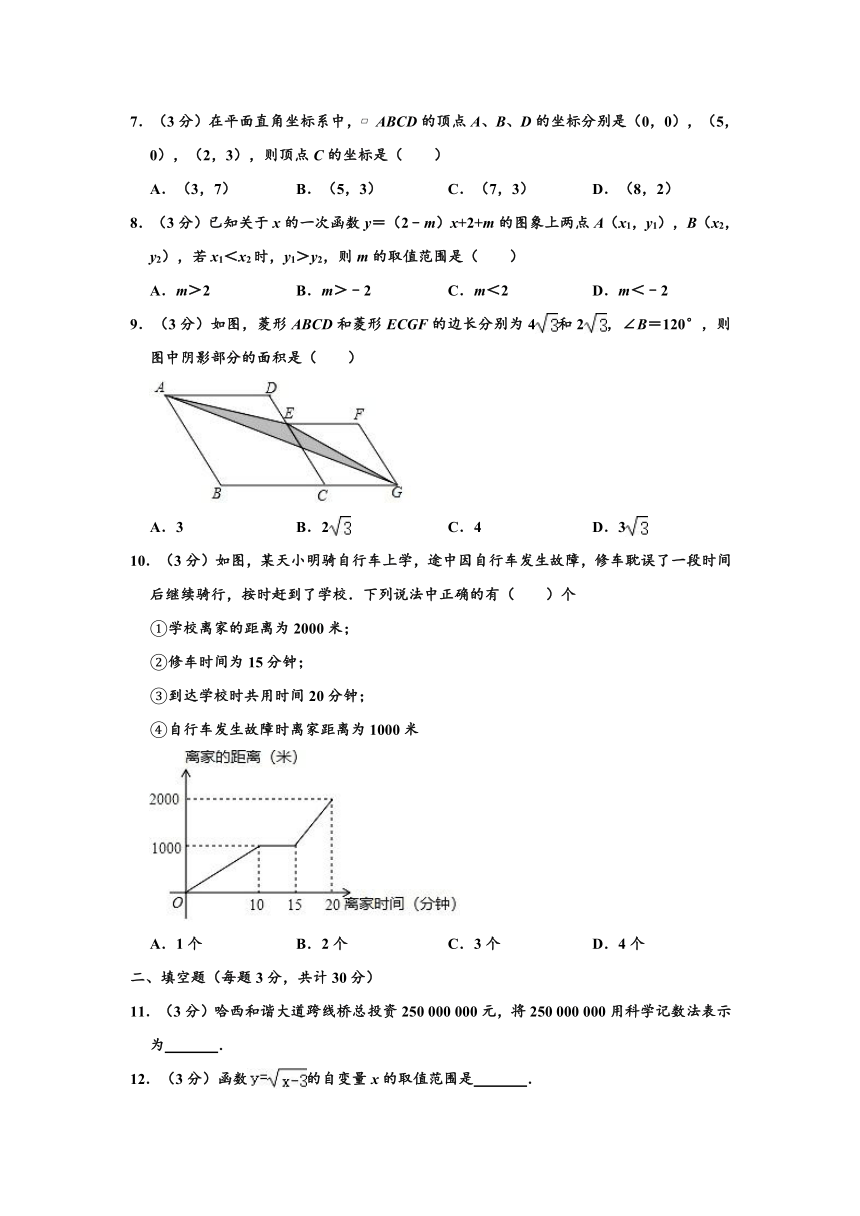
10.(3分)如图,某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.下列说法中正确的有( )个
①学校离家的距离为2000米;
②修车时间为15分钟;
③到达学校时共用时间20分钟;
④自行车发生故障时离家距离为1000米
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共计30分)
11.(3分)哈西和谐大道跨线桥总投资250 000 000元,将250 000 000用科学记数法表示为 .
12.(3分)函数的自变量x的取值范围是 .
13.(3分)经过(﹣1,2)的正比例函数的表达式是 .
14.(3分)已知菱形的周长为40cm,两条对角线之比为3:4,则菱形的面积为 cm2.
15.(3分)函数的图象如图所示,当y=0时,x= .
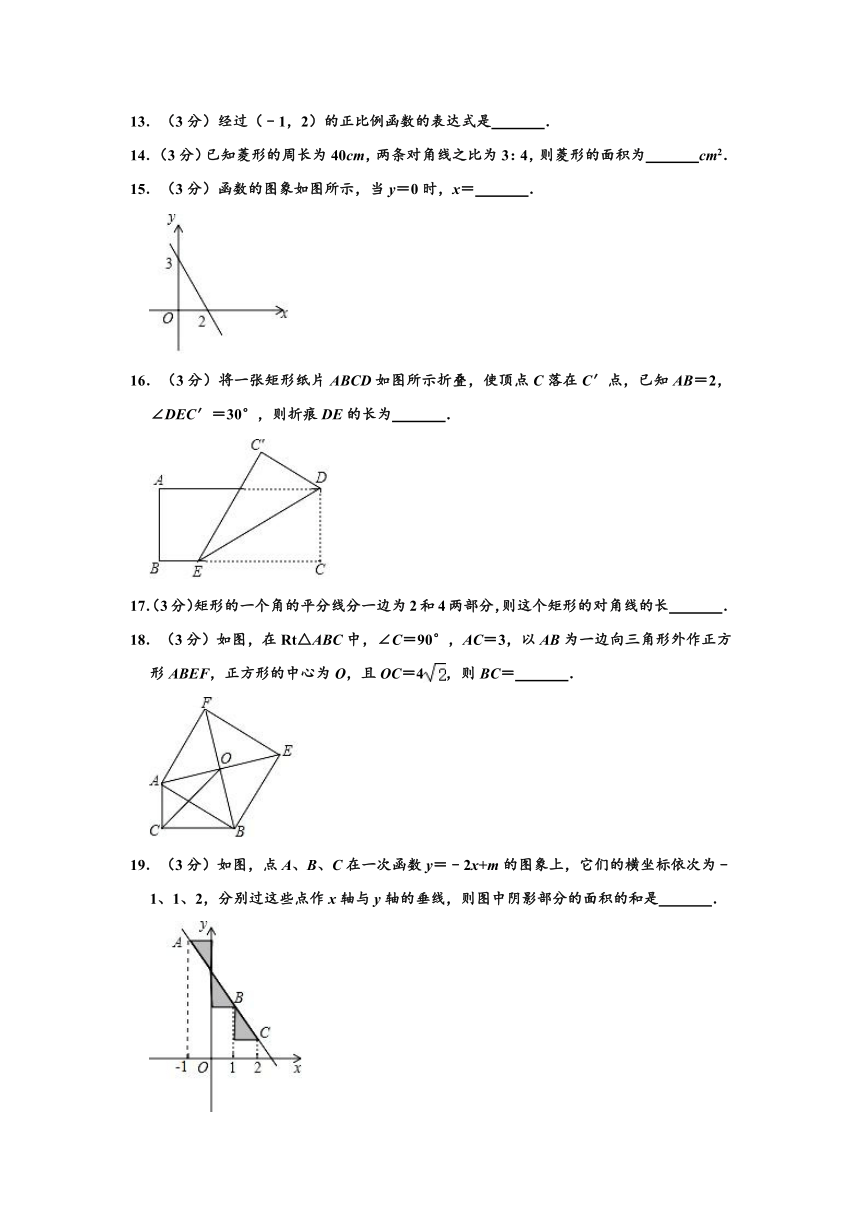
16.(3分)将一张矩形纸片ABCD如图所示折叠,使顶点C落在C′点,已知AB=2,∠DEC′=30°,则折痕DE的长为 .
17.(3分)矩形的一个角的平分线分一边为2和4两部分,则这个矩形的对角线的长 .
18.(3分)如图,在Rt△ABC中,∠C=90°,AC=3,以AB为一边向三角形外作正方形ABEF,正方形的中心为O,且OC=4,则BC= .
19.(3分)如图,点A、B、C在一次函数y=﹣2x+m的图象上,它们的横坐标依次为﹣1、1、2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积的和是 .
20.(3分)如图,在矩形ABCD中,AD=2AB=12,连接AC,E在BC上,连接AE、ED,若∠EAC=45°,则ED= .
三、解答题(21-25题各8分,26题、27题各10分)
21.(8分)先化简,再求值÷(2m﹣),其中m=﹣1.
22.(8分)如图,在8×5的正方形网格中(小正方形的边长均为1)有线段AB,其端点均在小正方形的顶点上,请按要求在方格纸中画出图形:
(1)画一个以线段AB为一边的菱形ABCD,且点C、D均在小正方形的顶点上;
(2)画一个以线段BC为一腰的面积为12.5的等腰三角形BCE,且点E在小正方形的顶点上;
(3)连接DE,请直接写出线段DE的长.
23.(8分)如图,点A、B与建筑物底部D在一直线上,建筑物与地面垂直,从点A测得建筑物顶部点C的仰角∠DAC=30°,从点B测得建筑物顶部点C的仰角∠DBC是60°,筑物的高CD=20cm,求AB的长.
24.(8分)一次函数y=kx+b的图象经过点(3,﹣2)和点(﹣1,6).
(1)求出该一次函数的解析式;
(2)求该图象与x轴的交点A的坐标,与y轴的交点B的坐标,并画出函数的图象;
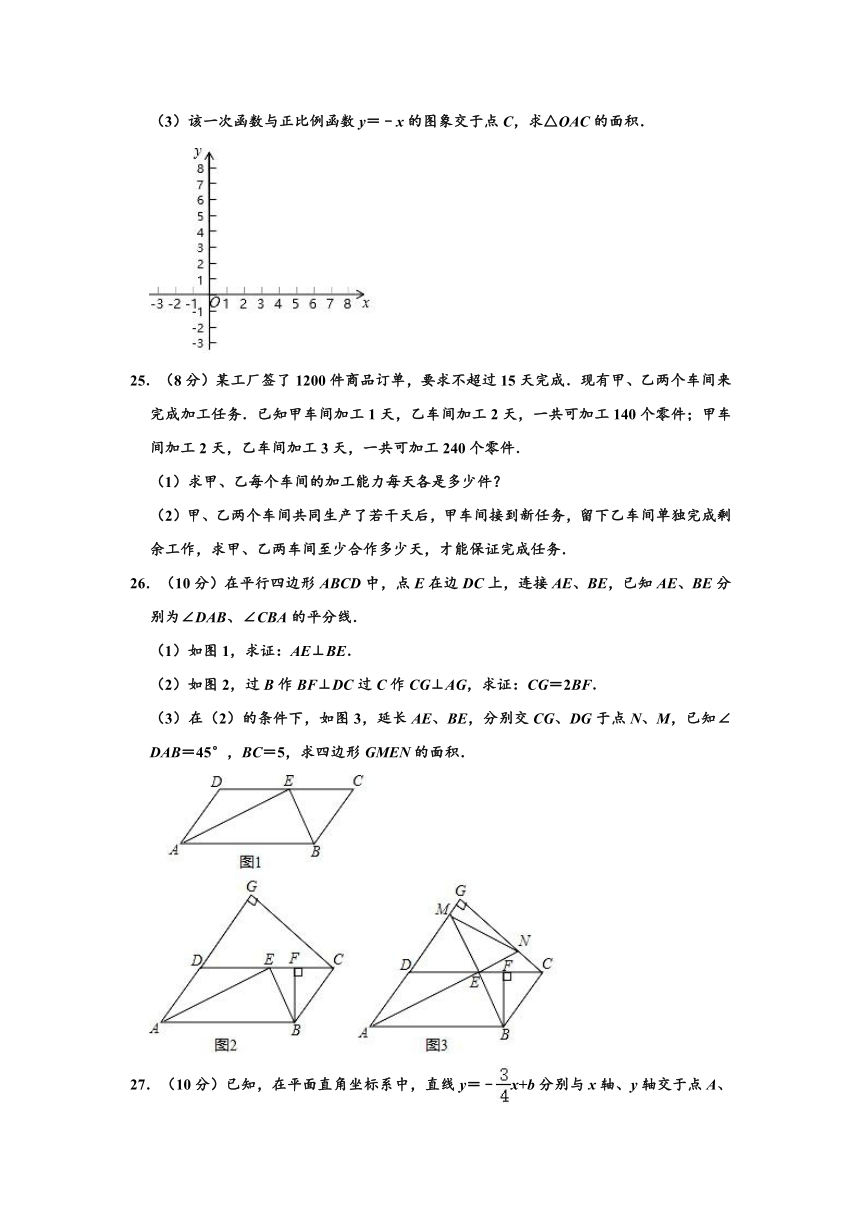
(3)该一次函数与正比例函数y=﹣x的图象交于点C,求△OAC的面积.
25.(8分)某工厂签了1200件商品订单,要求不超过15天完成.现有甲、乙两个车间来完成加工任务.已知甲车间加工1天,乙车间加工2天,一共可加工140个零件;甲车间加工2天,乙车间加工3天,一共可加工240个零件.
(1)求甲、乙每个车间的加工能力每天各是多少件?
(2)甲、乙两个车间共同生产了若干天后,甲车间接到新任务,留下乙车间单独完成剩余工作,求甲、乙两车间至少合作多少天,才能保证完成任务.
26.(10分)在平行四边形ABCD中,点E在边DC上,连接AE、BE,已知AE、BE分别为∠DAB、∠CBA的平分线.
(1)如图1,求证:AE⊥BE.
(2)如图2,过B作BF⊥DC过C作CG⊥AG,求证:CG=2BF.
(3)在(2)的条件下,如图3,延长AE、BE,分别交CG、DG于点N、M,已知∠DAB=45°,BC=5,求四边形GMEN的面积.
27.(10分)已知,在平面直角坐标系中,直线y=﹣x+b分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),点C为AB中点.
(1)求点B的坐标;
(2)点M为直线AB上的一个动点,过点M作x轴的垂线,交直线OC于点Q,设点M的横坐标为m,线段MQ的长度为d,求d与m的函数关系式(请直接写出自变量m的取值范围)
(3)当点M在线段AB(点M不与A、B重合)上运动时,在坐标系内是否存在一点N,使得以O、B、M、N为顶点的四边形为菱形?若存在,直接写出N点的坐标;若不存在,请说明理由.
参考答案
一、选择题(每小题3分,共30分)
1.(3分)下列各组线段中,能构成直角三角形的是( )
A.2,3,4 B.3,4,6 C.5,12,13 D.4,6,7
解:A、22+32=13≠42,故A选项构成不是直角三角形;
B、32+42=25≠62,故B选项构成不是直角三角形;
C、52+122=169=132,故C选项构成是直角三角形;
D、42+62=52≠72,故D选项构成不是直角三角形.
故选:C.
2.(3分)顺次连接矩形四边中点得到的四边形一定是( )
A.正方形 B.矩形 C.菱形 D.平行四边形
解:如图,连接AC、BD.
在△ABD中,
∵AH=HD,AE=EB,
∴EH=BD,
同理FG=BD,HG=AC,EF=AC,
又∵在矩形ABCD中,AC=BD,
∴EH=HG=GF=FE,
∴四边形EFGH为菱形.
故选:C.
3.(3分)如图,已知在?ABCD中,∠A+∠C=140°,则∠B的度数是( )
A.110° B.120° C.140° D.160°
解:∵平行四边形ABCD,
∴∠A+∠B=180°,∠A=∠C,
∵∠A+∠C=140°,
∴∠A=∠C=70°,
∴∠B=110°,
故选:A.
4.(3分)矩形ABCD的对角线AC、BD相交于点O,AB=4cm,∠AOB=60°,则这个矩形的对角线长是( )
A.2cm B.4cm C.6cm D.8cm
解:如图所示:
∵四边形ABCD是矩形,
∴AO=CO,BO=DO,AC=BD,
∴AO=BO,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AO=AB=4cm,
∴AC=2AO=8cm.
故选:D.
5.(3分)如图,一只蚂蚁从正方体的下底面A点沿着侧面爬到上底面B点,正方体棱长为3cm,则蚂蚁所走过的最短路径是( )
A.3cm B.6cm C.3cm D.3cm
解:如图所示,将正面和右面展开在同一平面内,
连接AB,则AB长即为蚂蚁所走过的最短路径,
∵∠ACB=90°,AC=6cm,BC=3cm,
∴Rt△ABC中,AB===(cm),
∴蚂蚁所走过的最短路径是cm,
故选:D.
6.(3分)如图,四边形ABCD是正方形,△CDE是等边三角形,连接AE,则∠AED的度数为( )
A.10° B.15° C.20° D.30°
解:∵四边形ABCD是正方形,
∴DA=DC,∠ADC=90°,
∵△CDE是等边三角形,
∴DC=DE,∠CDE=60°,
∴DA=DE,∠ADE=150°,
∴∠DAE=∠DEA=(180°﹣150°)=15°.
故选:B.
7.(3分)在平面直角坐标系中,?ABCD的顶点A、B、D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )
A.(3,7) B.(5,3) C.(7,3) D.(8,2)
解:如图,∵?ABCD的顶点A(0,0),B(5,0),D(2,3),
∴AB=CD=5,C点纵坐标与D点纵坐标相同,
∴顶点C的坐标是;(7,3).
故选:C.
8.(3分)已知关于x的一次函数y=(2﹣m)x+2+m的图象上两点A(x1,y1),B(x2,y2),若x1<x2时,y1>y2,则m的取值范围是( )
A.m>2 B.m>﹣2 C.m<2 D.m<﹣2
解:∵当x1<x2时,y1>y2,
∴y随x的增大而减小,
∴2﹣m<0,
∴m>2.
故选:A.
9.(3分)如图,菱形ABCD和菱形ECGF的边长分别为4和2,∠B=120°,则图中阴影部分的面积是( )
A.3 B.2 C.4 D.3
解:如图,设AG交CE于点H,
∵菱形ABCD的边AB∥CD,
∴△GCE∽△GAB,
∴CH:AB=GC:GB,
即CH:4=2:6,
解得CH=,
所以,EH=CE﹣CH=2﹣=,
∵∠B=120°,
∴∠BCD=∠FEC=180°﹣120°=60°,
∴点B到CD的距离为4×=6,
点F到CE的距离为2×=3,
∴阴影部分的面积=S△AEH+S△GEH
=××(6+3)=3.
故选:D.
10.(3分)如图,某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.下列说法中正确的有( )个
①学校离家的距离为2000米;
②修车时间为15分钟;
③到达学校时共用时间20分钟;
④自行车发生故障时离家距离为1000米
A.1个 B.2个 C.3个 D.4个
解:由图象可知:
①学校离家的距离为2000米,故①说法正确;
②15﹣10=5(分钟),即修车时间为15分钟,故②说法错误,
③到达学校时共用时间20分钟,故③说法正确;
④自行车发生故障时离家距离为:2000﹣1000=1000(米),故④说法正确.
所以正确的说法有3个.
故选:C.
二、填空题(每题3分,共计30分)
11.(3分)哈西和谐大道跨线桥总投资250 000 000元,将250 000 000用科学记数法表示为 2.5×108 .
解:250 000 000=2.5×108,
故答案为:2.5×108.
12.(3分)函数的自变量x的取值范围是 x≥3 .
解:根据题意得,x﹣3≥0,
解得x≥3.
故答案为:x≥3.
13.(3分)经过(﹣1,2)的正比例函数的表达式是 y=﹣2x .
解:设正比例函数解析式为y=kx,
∵图象经过(﹣1,2),
∴2=﹣k,
解得:k=﹣2,
则正比例函数解析式为:y=﹣2x,
故答案为:y=﹣2x.
14.(3分)已知菱形的周长为40cm,两条对角线之比为3:4,则菱形的面积为 96 cm2.
解:设两条对角线长分别为3x,4x,
根据勾股定理可得()2+()2=102,
解之得,x=4,
则两条对角线长分别为12cm、16cm,
∴菱形的面积=12×16÷2=96cm2.
故答案为96.
15.(3分)函数的图象如图所示,当y=0时,x= 2 .
解:y=0时,即与x轴的交点,
自变量x的值是2.
故答案为:2.
16.(3分)将一张矩形纸片ABCD如图所示折叠,使顶点C落在C′点,已知AB=2,∠DEC′=30°,则折痕DE的长为 4 .
解:∵四边形ABCD是矩形,
∴∠C=90°,
∵∠DEC'=30°,
∴∠DEC=30°,
∴DE=2DC=2AB=4.
故答案为:4.
17.(3分)矩形的一个角的平分线分一边为2和4两部分,则这个矩形的对角线的长 2或2 .
解:如图所示:
∵△ABCD是平行四边形,
∴AD∥BC,AC=BD,∠C=90°,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠AEB=∠ABE,
∴AB=AE;
当AE=4时,AB=4;AD=6,
∴BD===2;
当AE=4时,AB=4,AD=6,
∴BD===2;
即这个矩形的对角线的长为 2或 2;
故答案为:2或 2.
18.(3分)如图,在Rt△ABC中,∠C=90°,AC=3,以AB为一边向三角形外作正方形ABEF,正方形的中心为O,且OC=4,则BC= 5. .
解:如图,以C为坐标原点建立直角坐标系,CB为x轴,CA为y轴,则A(0,3),
作EQ⊥x轴于点Q,OM⊥x轴于点M,
设B(x,0),由于O点为以AB一边向三角形外作正方形ABEF的中心,
∴AB=BE,∠ABE=90°,
∵∠ACB=90°,
∴∠BAC+∠ABC=90°,∠ABC+∠EBQ=90°,
∴∠BAC=∠EBQ,
在△ABC和△BEQ中,
,
∴△ACB≌△BQE(AAS),
∴AC=BQ=3,BC=EQ,
设BC=EQ=x,
∴O为AE中点,
∴OM为梯形ACQE的中位线,
∴OM=,
又∵CM=CQ=,
∴O点坐标为(,),
根据题意得:OC=4,
根据勾股定理,得
(4)2=2()2
解得x=5,
则BC=5.
故答案为:5.
19.(3分)如图,点A、B、C在一次函数y=﹣2x+m的图象上,它们的横坐标依次为﹣1、1、2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积的和是 3 .
解:如图所示,将A、B、C的横坐标代入到一次函数中;
解得A(﹣1,m+2),B(1,m﹣2),C(2,m﹣4).
由一次函数的性质可知,三个阴影部分三角形全等,底边长为2﹣1=1,高为(m﹣2)﹣(m﹣4)=2,
可求的阴影部分面积为:S=×1×2×3=3.
所以应填:3.
20.(3分)如图,在矩形ABCD中,AD=2AB=12,连接AC,E在BC上,连接AE、ED,若∠EAC=45°,则ED= 2 .
解:∵在矩形ABCD中,BC=AD=2AB=12,
∴AB=DC=6,
∴AC==6,
如图,过点C作CF垂直AE的延长线于点F,
∵∠EAC=45°,
∴AF=CF=AC=3,
设BE=x,则EC=BC﹣BE=12﹣x,
设EF=y,则AE=AF﹣EF=3﹣y,
∵∠B=∠EFC=90°,∠AEB=∠CEF,
∴△ABE∽△CFE,
∴==,
即==,
解得,y=,
所以x=2.
则CE=12﹣2=10,DC=6,
在Rt△CDE中,根据勾股定理,得
ED==2.
故答案为:2.
三、解答题(21-25题各8分,26题、27题各10分)
21.(8分)先化简,再求值÷(2m﹣),其中m=﹣1.
解:当m=﹣1时,
原式=÷
=?
=
=
=,
22.(8分)如图,在8×5的正方形网格中(小正方形的边长均为1)有线段AB,其端点均在小正方形的顶点上,请按要求在方格纸中画出图形:
(1)画一个以线段AB为一边的菱形ABCD,且点C、D均在小正方形的顶点上;
(2)画一个以线段BC为一腰的面积为12.5的等腰三角形BCE,且点E在小正方形的顶点上;
(3)连接DE,请直接写出线段DE的长.
解:(1)如图1,理由是:
∵AB=DC=5,
AD=BC==5,
∴AB=CD=AD=BC,
∴四边形ABCD为菱形;
(2)如图2,理由是:
由勾股定理得:BE==5,BC==5,EC==,
∴EC2=BE2+BC2,
∴△BEC是等腰直角三角形,
∴S△BEC=×5×5=12.5;
(3)如图3,DE==,
23.(8分)如图,点A、B与建筑物底部D在一直线上,建筑物与地面垂直,从点A测得建筑物顶部点C的仰角∠DAC=30°,从点B测得建筑物顶部点C的仰角∠DBC是60°,筑物的高CD=20cm,求AB的长.
解:在Rt△CDB中,sin∠DBC=,
∴BC===40,
∵∠DAC=30°,∠DBC=60°,
∴∠ACB=∠DBC﹣∠DAC=30°,
∴∠ACB=∠DAC,
∴AB=BC=40(cm),
答:AB的长为40cm.
24.(8分)一次函数y=kx+b的图象经过点(3,﹣2)和点(﹣1,6).
(1)求出该一次函数的解析式;
(2)求该图象与x轴的交点A的坐标,与y轴的交点B的坐标,并画出函数的图象;
(3)该一次函数与正比例函数y=﹣x的图象交于点C,求△OAC的面积.
解:(1)设一次函数的解析式为y=kx+b,则有,
解得,
∴一次函数的解析式为y=﹣2x+4.
(2)对于直线y=﹣2x+4,令x=0,得到y=4,令y=0得到x=2,
∴A(2,0),B(0,4),
画出函数的图象如图所示;
(3)由,解得,
∴C(4,﹣4),
∴S△AOC=×2×4=4.
25.(8分)某工厂签了1200件商品订单,要求不超过15天完成.现有甲、乙两个车间来完成加工任务.已知甲车间加工1天,乙车间加工2天,一共可加工140个零件;甲车间加工2天,乙车间加工3天,一共可加工240个零件.
(1)求甲、乙每个车间的加工能力每天各是多少件?
(2)甲、乙两个车间共同生产了若干天后,甲车间接到新任务,留下乙车间单独完成剩余工作,求甲、乙两车间至少合作多少天,才能保证完成任务.
解:(1)设甲车间的加工能力每天是x件,乙车间的加工能力每天是y件,
依题意得:.
解得.
答:甲车间的加工能力每天是60件,乙车间的加工能力每天是40件;
(2)设甲、乙两车间合作m天,才能保证完成任务.
根据题意得:m+[1200﹣(40+60)m]÷40≤15,
解得m≥10.
答:甲、乙两车间至少合作10天,才能保证完成任务.
26.(10分)在平行四边形ABCD中,点E在边DC上,连接AE、BE,已知AE、BE分别为∠DAB、∠CBA的平分线.
(1)如图1,求证:AE⊥BE.
(2)如图2,过B作BF⊥DC过C作CG⊥AG,求证:CG=2BF.
(3)在(2)的条件下,如图3,延长AE、BE,分别交CG、DG于点N、M,已知∠DAB=45°,BC=5,求四边形GMEN的面积.
【解答】(1)证明:如图1中,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAB+∠ABC=180°,
∵∠EAB=∠DAB,∠EBA=∠ABC,
∴∠EAB+∠EBC=(∠DAB+∠ABC)=90°,
∴∠AEB=180°﹣(∠EAB+∠EBA)=90°.
(2)证明:如图2中,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,AD=BC,
∴∠AED=∠EAB,∠CEB=∠EBC,
∵∠EAD=∠EAB,∠EBA=∠EBC,
∴∠EAD=∠DEA,∠CEB=∠CBE,
∴AD=DE,BC=EC,
∴CD=2BC,
∵AG∥BC,
∴∠CDG=∠FCB,
∵CG⊥AG,BF⊥CD,
∴∠G=∠BFC=90°,
∴△DGC∽△CFB,
∴==2,
∴CG=2BF.
(3)解:如图3中,连接EG.
∵CD=2BC,BC=5,
∴CD=5,
∵∠DAB=45°,CD∥AB,
∴∠GDC=∠DAB=45°,
∵∠DGC=90°,
∴∠GDC=∠GCD=45°,
∴△CDG是等腰直角三角形,
∵DE=EC,
∴GE⊥CD,GE=DE=CE,
∵∠MEN=∠GEC=90°,
∴∠MEG=∠NEC,
∵∠EGM=∠ECN=45°,EG=EC,
∴△EGM≌△ECN(ASA),
∴S△EGM=S△ECN,
∴S四边形EMGN=S△GEC=×5×5=.
27.(10分)已知,在平面直角坐标系中,直线y=﹣x+b分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),点C为AB中点.
(1)求点B的坐标;
(2)点M为直线AB上的一个动点,过点M作x轴的垂线,交直线OC于点Q,设点M的横坐标为m,线段MQ的长度为d,求d与m的函数关系式(请直接写出自变量m的取值范围)
(3)当点M在线段AB(点M不与A、B重合)上运动时,在坐标系内是否存在一点N,使得以O、B、M、N为顶点的四边形为菱形?若存在,直接写出N点的坐标;若不存在,请说明理由.
解:(1)∵直线y=﹣x+b过点A(8,0),
∴0=﹣6+b,解得:b=6,
∴直线AB的解析式为y=﹣x+6.
令y=﹣x+6中x=0,则y=6,
∴点B的坐标为(0,6).
(2)依照题意画出图形,如图1所示.
∵A(8,0),B(0,6),且点C为AB的中点,
∴C(4,3).
设直线OC的解析式为y=kx(k≠0),
则有3=4k,解得:k=,
∴直线OC的解析式为y=x.
∵点M在直线AB上,点Q在直线OC上,点M的横坐标为m,MQ⊥x轴,
∴M(m,﹣m+6),Q(m,m).
当m<4时,d=﹣m+6﹣m=﹣m+6;
当m>4时,d=m﹣(﹣m+6)=m﹣6.
故d=;
(3)假设存在,设点M的坐标为(n,﹣n+6)(0<n<8).
∵点P在第一象限,
∴以O,B,M,N为顶点的四边形为菱形有两种情况:
①以BM为对角线时,如图2所示.
∵四边形OMNB为菱形,B(0,6),
∴OM=OB=6=,
解得:n=或n=0(舍去),
∴点M(,),
则点N(,);
②以OM为对角线时,如图3所示.
此时点M在第一象限,但点N在第四象限,故此种情况不合适.
故N点坐标为(,).
一、选择题
1.(3分)下列各组线段中,能构成直角三角形的是( )
A.2,3,4 B.3,4,6 C.5,12,13 D.4,6,7
2.(3分)顺次连接矩形四边中点得到的四边形一定是( )
A.正方形 B.矩形 C.菱形 D.平行四边形
3.(3分)如图,已知在?ABCD中,∠A+∠C=140°,则∠B的度数是( )
A.110° B.120° C.140° D.160°
4.(3分)矩形ABCD的对角线AC、BD相交于点O,AB=4cm,∠AOB=60°,则这个矩形的对角线长是( )
A.2cm B.4cm C.6cm D.8cm
5.(3分)如图,一只蚂蚁从正方体的下底面A点沿着侧面爬到上底面B点,正方体棱长为3cm,则蚂蚁所走过的最短路径是( )
A.3cm B.6cm C.3cm D.3cm
6.(3分)如图,四边形ABCD是正方形,△CDE是等边三角形,连接AE,则∠AED的度数为( )
A.10° B.15° C.20° D.30°
7.(3分)在平面直角坐标系中,?ABCD的顶点A、B、D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )
A.(3,7) B.(5,3) C.(7,3) D.(8,2)
8.(3分)已知关于x的一次函数y=(2﹣m)x+2+m的图象上两点A(x1,y1),B(x2,y2),若x1<x2时,y1>y2,则m的取值范围是( )
A.m>2 B.m>﹣2 C.m<2 D.m<﹣2
9.(3分)如图,菱形ABCD和菱形ECGF的边长分别为4和2,∠B=120°,则图中阴影部分的面积是( )
A.3 B.2 C.4 D.3
10.(3分)如图,某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.下列说法中正确的有( )个
①学校离家的距离为2000米;
②修车时间为15分钟;
③到达学校时共用时间20分钟;
④自行车发生故障时离家距离为1000米
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共计30分)
11.(3分)哈西和谐大道跨线桥总投资250 000 000元,将250 000 000用科学记数法表示为 .
12.(3分)函数的自变量x的取值范围是 .
13.(3分)经过(﹣1,2)的正比例函数的表达式是 .
14.(3分)已知菱形的周长为40cm,两条对角线之比为3:4,则菱形的面积为 cm2.
15.(3分)函数的图象如图所示,当y=0时,x= .
16.(3分)将一张矩形纸片ABCD如图所示折叠,使顶点C落在C′点,已知AB=2,∠DEC′=30°,则折痕DE的长为 .
17.(3分)矩形的一个角的平分线分一边为2和4两部分,则这个矩形的对角线的长 .
18.(3分)如图,在Rt△ABC中,∠C=90°,AC=3,以AB为一边向三角形外作正方形ABEF,正方形的中心为O,且OC=4,则BC= .
19.(3分)如图,点A、B、C在一次函数y=﹣2x+m的图象上,它们的横坐标依次为﹣1、1、2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积的和是 .
20.(3分)如图,在矩形ABCD中,AD=2AB=12,连接AC,E在BC上,连接AE、ED,若∠EAC=45°,则ED= .
三、解答题(21-25题各8分,26题、27题各10分)
21.(8分)先化简,再求值÷(2m﹣),其中m=﹣1.
22.(8分)如图,在8×5的正方形网格中(小正方形的边长均为1)有线段AB,其端点均在小正方形的顶点上,请按要求在方格纸中画出图形:
(1)画一个以线段AB为一边的菱形ABCD,且点C、D均在小正方形的顶点上;
(2)画一个以线段BC为一腰的面积为12.5的等腰三角形BCE,且点E在小正方形的顶点上;
(3)连接DE,请直接写出线段DE的长.
23.(8分)如图,点A、B与建筑物底部D在一直线上,建筑物与地面垂直,从点A测得建筑物顶部点C的仰角∠DAC=30°,从点B测得建筑物顶部点C的仰角∠DBC是60°,筑物的高CD=20cm,求AB的长.
24.(8分)一次函数y=kx+b的图象经过点(3,﹣2)和点(﹣1,6).
(1)求出该一次函数的解析式;
(2)求该图象与x轴的交点A的坐标,与y轴的交点B的坐标,并画出函数的图象;
(3)该一次函数与正比例函数y=﹣x的图象交于点C,求△OAC的面积.
25.(8分)某工厂签了1200件商品订单,要求不超过15天完成.现有甲、乙两个车间来完成加工任务.已知甲车间加工1天,乙车间加工2天,一共可加工140个零件;甲车间加工2天,乙车间加工3天,一共可加工240个零件.
(1)求甲、乙每个车间的加工能力每天各是多少件?
(2)甲、乙两个车间共同生产了若干天后,甲车间接到新任务,留下乙车间单独完成剩余工作,求甲、乙两车间至少合作多少天,才能保证完成任务.
26.(10分)在平行四边形ABCD中,点E在边DC上,连接AE、BE,已知AE、BE分别为∠DAB、∠CBA的平分线.
(1)如图1,求证:AE⊥BE.
(2)如图2,过B作BF⊥DC过C作CG⊥AG,求证:CG=2BF.
(3)在(2)的条件下,如图3,延长AE、BE,分别交CG、DG于点N、M,已知∠DAB=45°,BC=5,求四边形GMEN的面积.
27.(10分)已知,在平面直角坐标系中,直线y=﹣x+b分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),点C为AB中点.
(1)求点B的坐标;
(2)点M为直线AB上的一个动点,过点M作x轴的垂线,交直线OC于点Q,设点M的横坐标为m,线段MQ的长度为d,求d与m的函数关系式(请直接写出自变量m的取值范围)
(3)当点M在线段AB(点M不与A、B重合)上运动时,在坐标系内是否存在一点N,使得以O、B、M、N为顶点的四边形为菱形?若存在,直接写出N点的坐标;若不存在,请说明理由.
参考答案
一、选择题(每小题3分,共30分)
1.(3分)下列各组线段中,能构成直角三角形的是( )
A.2,3,4 B.3,4,6 C.5,12,13 D.4,6,7
解:A、22+32=13≠42,故A选项构成不是直角三角形;
B、32+42=25≠62,故B选项构成不是直角三角形;
C、52+122=169=132,故C选项构成是直角三角形;
D、42+62=52≠72,故D选项构成不是直角三角形.
故选:C.
2.(3分)顺次连接矩形四边中点得到的四边形一定是( )
A.正方形 B.矩形 C.菱形 D.平行四边形
解:如图,连接AC、BD.
在△ABD中,
∵AH=HD,AE=EB,
∴EH=BD,
同理FG=BD,HG=AC,EF=AC,
又∵在矩形ABCD中,AC=BD,
∴EH=HG=GF=FE,
∴四边形EFGH为菱形.
故选:C.
3.(3分)如图,已知在?ABCD中,∠A+∠C=140°,则∠B的度数是( )
A.110° B.120° C.140° D.160°
解:∵平行四边形ABCD,
∴∠A+∠B=180°,∠A=∠C,
∵∠A+∠C=140°,
∴∠A=∠C=70°,
∴∠B=110°,
故选:A.
4.(3分)矩形ABCD的对角线AC、BD相交于点O,AB=4cm,∠AOB=60°,则这个矩形的对角线长是( )
A.2cm B.4cm C.6cm D.8cm
解:如图所示:
∵四边形ABCD是矩形,
∴AO=CO,BO=DO,AC=BD,
∴AO=BO,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AO=AB=4cm,
∴AC=2AO=8cm.
故选:D.
5.(3分)如图,一只蚂蚁从正方体的下底面A点沿着侧面爬到上底面B点,正方体棱长为3cm,则蚂蚁所走过的最短路径是( )
A.3cm B.6cm C.3cm D.3cm
解:如图所示,将正面和右面展开在同一平面内,
连接AB,则AB长即为蚂蚁所走过的最短路径,
∵∠ACB=90°,AC=6cm,BC=3cm,
∴Rt△ABC中,AB===(cm),
∴蚂蚁所走过的最短路径是cm,
故选:D.
6.(3分)如图,四边形ABCD是正方形,△CDE是等边三角形,连接AE,则∠AED的度数为( )
A.10° B.15° C.20° D.30°
解:∵四边形ABCD是正方形,
∴DA=DC,∠ADC=90°,
∵△CDE是等边三角形,
∴DC=DE,∠CDE=60°,
∴DA=DE,∠ADE=150°,
∴∠DAE=∠DEA=(180°﹣150°)=15°.
故选:B.
7.(3分)在平面直角坐标系中,?ABCD的顶点A、B、D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )
A.(3,7) B.(5,3) C.(7,3) D.(8,2)
解:如图,∵?ABCD的顶点A(0,0),B(5,0),D(2,3),
∴AB=CD=5,C点纵坐标与D点纵坐标相同,
∴顶点C的坐标是;(7,3).
故选:C.
8.(3分)已知关于x的一次函数y=(2﹣m)x+2+m的图象上两点A(x1,y1),B(x2,y2),若x1<x2时,y1>y2,则m的取值范围是( )
A.m>2 B.m>﹣2 C.m<2 D.m<﹣2
解:∵当x1<x2时,y1>y2,
∴y随x的增大而减小,
∴2﹣m<0,
∴m>2.
故选:A.
9.(3分)如图,菱形ABCD和菱形ECGF的边长分别为4和2,∠B=120°,则图中阴影部分的面积是( )
A.3 B.2 C.4 D.3
解:如图,设AG交CE于点H,
∵菱形ABCD的边AB∥CD,
∴△GCE∽△GAB,
∴CH:AB=GC:GB,
即CH:4=2:6,
解得CH=,
所以,EH=CE﹣CH=2﹣=,
∵∠B=120°,
∴∠BCD=∠FEC=180°﹣120°=60°,
∴点B到CD的距离为4×=6,
点F到CE的距离为2×=3,
∴阴影部分的面积=S△AEH+S△GEH
=××(6+3)=3.
故选:D.
10.(3分)如图,某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.下列说法中正确的有( )个
①学校离家的距离为2000米;
②修车时间为15分钟;
③到达学校时共用时间20分钟;
④自行车发生故障时离家距离为1000米
A.1个 B.2个 C.3个 D.4个
解:由图象可知:
①学校离家的距离为2000米,故①说法正确;
②15﹣10=5(分钟),即修车时间为15分钟,故②说法错误,
③到达学校时共用时间20分钟,故③说法正确;
④自行车发生故障时离家距离为:2000﹣1000=1000(米),故④说法正确.
所以正确的说法有3个.
故选:C.
二、填空题(每题3分,共计30分)
11.(3分)哈西和谐大道跨线桥总投资250 000 000元,将250 000 000用科学记数法表示为 2.5×108 .
解:250 000 000=2.5×108,
故答案为:2.5×108.
12.(3分)函数的自变量x的取值范围是 x≥3 .
解:根据题意得,x﹣3≥0,
解得x≥3.
故答案为:x≥3.
13.(3分)经过(﹣1,2)的正比例函数的表达式是 y=﹣2x .
解:设正比例函数解析式为y=kx,
∵图象经过(﹣1,2),
∴2=﹣k,
解得:k=﹣2,
则正比例函数解析式为:y=﹣2x,
故答案为:y=﹣2x.
14.(3分)已知菱形的周长为40cm,两条对角线之比为3:4,则菱形的面积为 96 cm2.
解:设两条对角线长分别为3x,4x,
根据勾股定理可得()2+()2=102,
解之得,x=4,
则两条对角线长分别为12cm、16cm,
∴菱形的面积=12×16÷2=96cm2.
故答案为96.
15.(3分)函数的图象如图所示,当y=0时,x= 2 .
解:y=0时,即与x轴的交点,
自变量x的值是2.
故答案为:2.
16.(3分)将一张矩形纸片ABCD如图所示折叠,使顶点C落在C′点,已知AB=2,∠DEC′=30°,则折痕DE的长为 4 .
解:∵四边形ABCD是矩形,
∴∠C=90°,
∵∠DEC'=30°,
∴∠DEC=30°,
∴DE=2DC=2AB=4.
故答案为:4.
17.(3分)矩形的一个角的平分线分一边为2和4两部分,则这个矩形的对角线的长 2或2 .
解:如图所示:
∵△ABCD是平行四边形,
∴AD∥BC,AC=BD,∠C=90°,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠AEB=∠ABE,
∴AB=AE;
当AE=4时,AB=4;AD=6,
∴BD===2;
当AE=4时,AB=4,AD=6,
∴BD===2;
即这个矩形的对角线的长为 2或 2;
故答案为:2或 2.
18.(3分)如图,在Rt△ABC中,∠C=90°,AC=3,以AB为一边向三角形外作正方形ABEF,正方形的中心为O,且OC=4,则BC= 5. .
解:如图,以C为坐标原点建立直角坐标系,CB为x轴,CA为y轴,则A(0,3),
作EQ⊥x轴于点Q,OM⊥x轴于点M,
设B(x,0),由于O点为以AB一边向三角形外作正方形ABEF的中心,
∴AB=BE,∠ABE=90°,
∵∠ACB=90°,
∴∠BAC+∠ABC=90°,∠ABC+∠EBQ=90°,
∴∠BAC=∠EBQ,
在△ABC和△BEQ中,
,
∴△ACB≌△BQE(AAS),
∴AC=BQ=3,BC=EQ,
设BC=EQ=x,
∴O为AE中点,
∴OM为梯形ACQE的中位线,
∴OM=,
又∵CM=CQ=,
∴O点坐标为(,),
根据题意得:OC=4,
根据勾股定理,得
(4)2=2()2
解得x=5,
则BC=5.
故答案为:5.
19.(3分)如图,点A、B、C在一次函数y=﹣2x+m的图象上,它们的横坐标依次为﹣1、1、2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积的和是 3 .
解:如图所示,将A、B、C的横坐标代入到一次函数中;
解得A(﹣1,m+2),B(1,m﹣2),C(2,m﹣4).
由一次函数的性质可知,三个阴影部分三角形全等,底边长为2﹣1=1,高为(m﹣2)﹣(m﹣4)=2,
可求的阴影部分面积为:S=×1×2×3=3.
所以应填:3.
20.(3分)如图,在矩形ABCD中,AD=2AB=12,连接AC,E在BC上,连接AE、ED,若∠EAC=45°,则ED= 2 .
解:∵在矩形ABCD中,BC=AD=2AB=12,
∴AB=DC=6,
∴AC==6,
如图,过点C作CF垂直AE的延长线于点F,
∵∠EAC=45°,
∴AF=CF=AC=3,
设BE=x,则EC=BC﹣BE=12﹣x,
设EF=y,则AE=AF﹣EF=3﹣y,
∵∠B=∠EFC=90°,∠AEB=∠CEF,
∴△ABE∽△CFE,
∴==,
即==,
解得,y=,
所以x=2.
则CE=12﹣2=10,DC=6,
在Rt△CDE中,根据勾股定理,得
ED==2.
故答案为:2.
三、解答题(21-25题各8分,26题、27题各10分)
21.(8分)先化简,再求值÷(2m﹣),其中m=﹣1.
解:当m=﹣1时,
原式=÷
=?
=
=
=,
22.(8分)如图,在8×5的正方形网格中(小正方形的边长均为1)有线段AB,其端点均在小正方形的顶点上,请按要求在方格纸中画出图形:
(1)画一个以线段AB为一边的菱形ABCD,且点C、D均在小正方形的顶点上;
(2)画一个以线段BC为一腰的面积为12.5的等腰三角形BCE,且点E在小正方形的顶点上;
(3)连接DE,请直接写出线段DE的长.
解:(1)如图1,理由是:
∵AB=DC=5,
AD=BC==5,
∴AB=CD=AD=BC,
∴四边形ABCD为菱形;
(2)如图2,理由是:
由勾股定理得:BE==5,BC==5,EC==,
∴EC2=BE2+BC2,
∴△BEC是等腰直角三角形,
∴S△BEC=×5×5=12.5;
(3)如图3,DE==,
23.(8分)如图,点A、B与建筑物底部D在一直线上,建筑物与地面垂直,从点A测得建筑物顶部点C的仰角∠DAC=30°,从点B测得建筑物顶部点C的仰角∠DBC是60°,筑物的高CD=20cm,求AB的长.
解:在Rt△CDB中,sin∠DBC=,
∴BC===40,
∵∠DAC=30°,∠DBC=60°,
∴∠ACB=∠DBC﹣∠DAC=30°,
∴∠ACB=∠DAC,
∴AB=BC=40(cm),
答:AB的长为40cm.
24.(8分)一次函数y=kx+b的图象经过点(3,﹣2)和点(﹣1,6).
(1)求出该一次函数的解析式;
(2)求该图象与x轴的交点A的坐标,与y轴的交点B的坐标,并画出函数的图象;
(3)该一次函数与正比例函数y=﹣x的图象交于点C,求△OAC的面积.
解:(1)设一次函数的解析式为y=kx+b,则有,
解得,
∴一次函数的解析式为y=﹣2x+4.
(2)对于直线y=﹣2x+4,令x=0,得到y=4,令y=0得到x=2,
∴A(2,0),B(0,4),
画出函数的图象如图所示;
(3)由,解得,
∴C(4,﹣4),
∴S△AOC=×2×4=4.
25.(8分)某工厂签了1200件商品订单,要求不超过15天完成.现有甲、乙两个车间来完成加工任务.已知甲车间加工1天,乙车间加工2天,一共可加工140个零件;甲车间加工2天,乙车间加工3天,一共可加工240个零件.
(1)求甲、乙每个车间的加工能力每天各是多少件?
(2)甲、乙两个车间共同生产了若干天后,甲车间接到新任务,留下乙车间单独完成剩余工作,求甲、乙两车间至少合作多少天,才能保证完成任务.
解:(1)设甲车间的加工能力每天是x件,乙车间的加工能力每天是y件,
依题意得:.
解得.
答:甲车间的加工能力每天是60件,乙车间的加工能力每天是40件;
(2)设甲、乙两车间合作m天,才能保证完成任务.
根据题意得:m+[1200﹣(40+60)m]÷40≤15,
解得m≥10.
答:甲、乙两车间至少合作10天,才能保证完成任务.
26.(10分)在平行四边形ABCD中,点E在边DC上,连接AE、BE,已知AE、BE分别为∠DAB、∠CBA的平分线.
(1)如图1,求证:AE⊥BE.
(2)如图2,过B作BF⊥DC过C作CG⊥AG,求证:CG=2BF.
(3)在(2)的条件下,如图3,延长AE、BE,分别交CG、DG于点N、M,已知∠DAB=45°,BC=5,求四边形GMEN的面积.
【解答】(1)证明:如图1中,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAB+∠ABC=180°,
∵∠EAB=∠DAB,∠EBA=∠ABC,
∴∠EAB+∠EBC=(∠DAB+∠ABC)=90°,
∴∠AEB=180°﹣(∠EAB+∠EBA)=90°.
(2)证明:如图2中,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,AD=BC,
∴∠AED=∠EAB,∠CEB=∠EBC,
∵∠EAD=∠EAB,∠EBA=∠EBC,
∴∠EAD=∠DEA,∠CEB=∠CBE,
∴AD=DE,BC=EC,
∴CD=2BC,
∵AG∥BC,
∴∠CDG=∠FCB,
∵CG⊥AG,BF⊥CD,
∴∠G=∠BFC=90°,
∴△DGC∽△CFB,
∴==2,
∴CG=2BF.
(3)解:如图3中,连接EG.
∵CD=2BC,BC=5,
∴CD=5,
∵∠DAB=45°,CD∥AB,
∴∠GDC=∠DAB=45°,
∵∠DGC=90°,
∴∠GDC=∠GCD=45°,
∴△CDG是等腰直角三角形,
∵DE=EC,
∴GE⊥CD,GE=DE=CE,
∵∠MEN=∠GEC=90°,
∴∠MEG=∠NEC,
∵∠EGM=∠ECN=45°,EG=EC,
∴△EGM≌△ECN(ASA),
∴S△EGM=S△ECN,
∴S四边形EMGN=S△GEC=×5×5=.
27.(10分)已知,在平面直角坐标系中,直线y=﹣x+b分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),点C为AB中点.
(1)求点B的坐标;
(2)点M为直线AB上的一个动点,过点M作x轴的垂线,交直线OC于点Q,设点M的横坐标为m,线段MQ的长度为d,求d与m的函数关系式(请直接写出自变量m的取值范围)
(3)当点M在线段AB(点M不与A、B重合)上运动时,在坐标系内是否存在一点N,使得以O、B、M、N为顶点的四边形为菱形?若存在,直接写出N点的坐标;若不存在,请说明理由.
解:(1)∵直线y=﹣x+b过点A(8,0),
∴0=﹣6+b,解得:b=6,
∴直线AB的解析式为y=﹣x+6.
令y=﹣x+6中x=0,则y=6,
∴点B的坐标为(0,6).
(2)依照题意画出图形,如图1所示.
∵A(8,0),B(0,6),且点C为AB的中点,
∴C(4,3).
设直线OC的解析式为y=kx(k≠0),
则有3=4k,解得:k=,
∴直线OC的解析式为y=x.
∵点M在直线AB上,点Q在直线OC上,点M的横坐标为m,MQ⊥x轴,
∴M(m,﹣m+6),Q(m,m).
当m<4时,d=﹣m+6﹣m=﹣m+6;
当m>4时,d=m﹣(﹣m+6)=m﹣6.
故d=;
(3)假设存在,设点M的坐标为(n,﹣n+6)(0<n<8).
∵点P在第一象限,
∴以O,B,M,N为顶点的四边形为菱形有两种情况:
①以BM为对角线时,如图2所示.
∵四边形OMNB为菱形,B(0,6),
∴OM=OB=6=,
解得:n=或n=0(舍去),
∴点M(,),
则点N(,);
②以OM为对角线时,如图3所示.
此时点M在第一象限,但点N在第四象限,故此种情况不合适.
故N点坐标为(,).
同课章节目录
