高中物理人教版必修1课后练习 2.5自由落体运动 Word版含解析
文档属性
| 名称 | 高中物理人教版必修1课后练习 2.5自由落体运动 Word版含解析 |

|
|
| 格式 | DOC | ||
| 文件大小 | 119.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-10 00:00:00 | ||
图片预览



文档简介
一、单项选择题
1.从同一高度做自由落体运动的甲、乙两个小铁球,甲的质量是乙的两倍,则( D )
A.甲比乙先落地,落地时甲的速度是乙的两倍
B.甲比乙先落地,落地时甲、乙的速度相同
C.甲、乙同时落地,落地时甲的速度是乙的两倍
D.甲、乙同时落地,落地时甲、乙的速度相同
解析:根据自由落体运动的公式h=gt2,t=,知落地时间与质量无关,所以两个物体同时落地.故D正确,A、B、C均错误.
2.已知广州地区的重力加速度为9.8 m/s2,在此地区物体做自由落体运动的说法中,正确的是( A )
A.下落过程,物体的速度每秒增加9.8 m/s
B.自由落体运动是一种匀速运动
C.释放物体瞬间,物体速度和加速度都为零
D.物体越重,下落的越快
解析:重力加速度为9.8 m/s2,故自由下落过程中物体的速度每秒增加9.8 m/s,故A正确;自由落体运动是初速度为零,加速度为g的匀加速直线运动,故B错误;释放物体瞬间,物体速度为零,加速度为g,故C错误;重力加速度与物体的质量无关,重物与轻物下落一样快,故D错误.
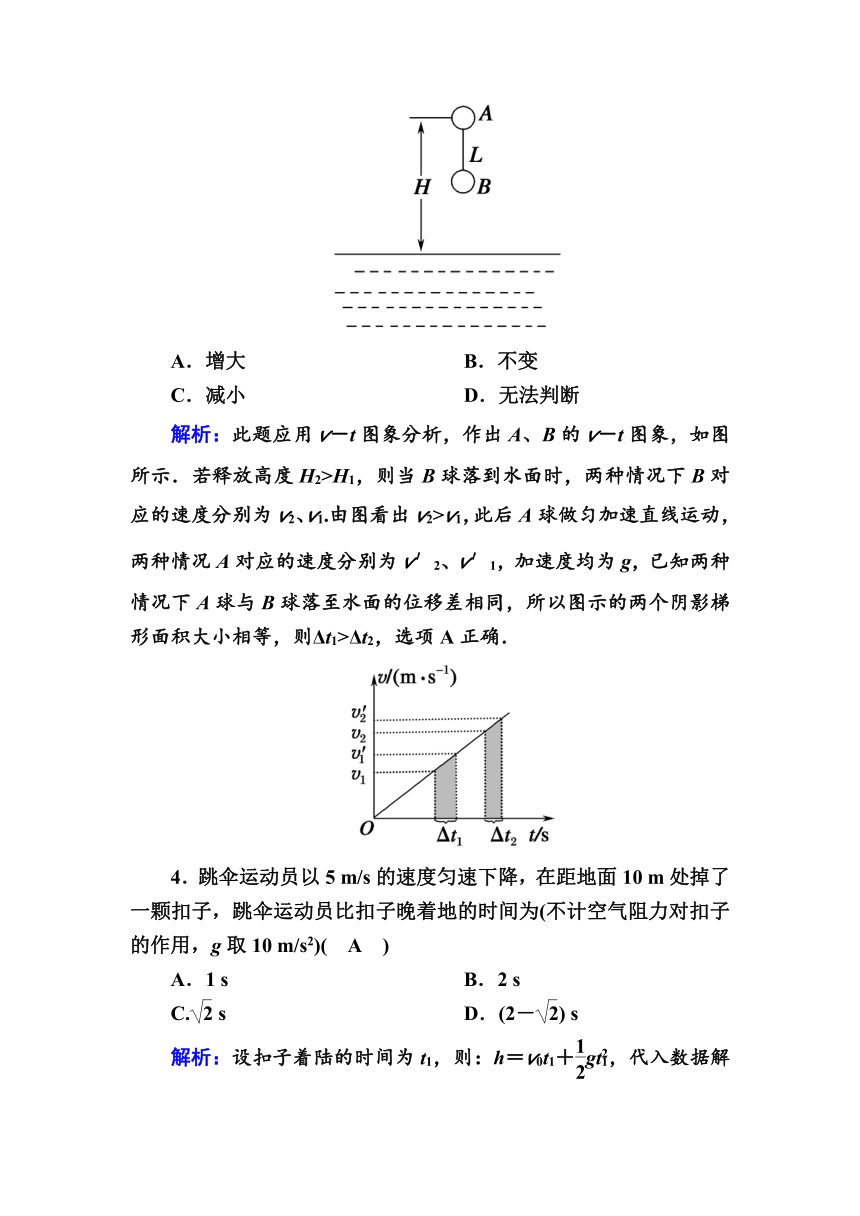
3.如图所示,A、B两小球用长为L的细线连接悬挂在空中.A距湖水水面高度为H,释放小球,让它们自由落下,测得它们落水声相差Δt.如果球A距湖面的高度H减小,则Δt将( A )
A.增大 B.不变
C.减小 D.无法判断
解析:此题应用v-t图象分析,作出A、B的v-t图象,如图所示.若释放高度H2>H1,则当B球落到水面时,两种情况下B对应的速度分别为v2、v1.由图看出v2>v1,此后A球做匀加速直线运动,两种情况A对应的速度分别为v′2、v′1,加速度均为g,已知两种情况下A球与B球落至水面的位移差相同,所以图示的两个阴影梯形面积大小相等,则Δt1>Δt2,选项A正确.
4.跳伞运动员以5 m/s的速度匀速下降,在距地面10 m处掉了一颗扣子,跳伞运动员比扣子晚着地的时间为(不计空气阻力对扣子的作用,g取10 m/s2)( A )
A.1 s B.2 s
C. s D.(2-) s
解析:设扣子着陆的时间为t1,则:h=v0t1+gt,代入数据解得t1=1 s.设跳伞运动员着陆时间为t2,则:h=v0t2,解得:t2=2 s,而Δt=t2-t1=1 s.故A正确,B、C、D错误.
5.取一根长2 m左右的细线,5个铁垫圈和一个金属盘.在线端系上第一个垫圈,隔12 cm再系一个,以后垫圈之间的距离分别为36 cm、60 cm、84 cm,如图所示.站在椅子上,向上提起线的上端,让线自由垂下,且第一个垫圈紧靠放在地上的金属盘.松手后开始计时,若不计空气阻力,则第2、3、4、5各垫圈( B )
A.落到盘上的声音时间间隔越来越大
B.落到盘上的声音时间间隔相等
C.依次落到盘上的速率关系为1∶∶∶2
D.依次落到盘上的时间关系为1∶(-1)∶(-)∶(2-)
解析:4个铁垫圈同时做自由落体运动,下降的位移之比为1∶3∶5∶7.可以看成一个铁垫圈自由下落,经过位移之比为1∶3∶5∶7.因为初速度为零的匀加速直线运动在相等时间内的位移之比为1∶3∶5∶7,知各垫圈落到盘中的时间间隔相等,故A错误,B正确.因为各垫圈落到盘中的时间间隔相等,则各垫圈依次落到盘中的时间比为1∶2∶3∶4,根据v=gt可知,速率之比为1∶2∶3∶4,故C、D错误.
二、多项选择题
6.一物体从一行星表面某高度处自由下落(不计表层大气阻力).自开始下落计时,得到物体离该行星表面的高度h随时间t变化的图象如图所示,则( AC )
A.行星表面重力加速度大小为8 m/s2
B.行星表面重力加速度大小为10 m/s2
C.物体落到行星表面时的速度大小为20 m/s
D.物体落到行星表面时的速度大小为25 m/s
解析:由图中可以看出物体从h=25 m处开始下落,在空中运动了t=2.5 s到达行星表面,根据h=at2,可以求出a=8 m/s2,故A正确;根据运动学公式可以算出v=at=20 m/s,可知C正确.
7.某物体做自由落体运动(g=10 m/s2),则( ACD )
A.第2 s内的平均速度为15 m/s
B.后一秒的位移总比前一秒的位移多5 m
C.前一秒的平均速度总比后一秒的平均速度小10 m/s
D.第7 s内的位移为65 m
解析:第2 s内的位移为h=g×22-g×12=15 m,所以第2 s内的平均速度为v== m/s=15 m/s,A正确;根据逐差法可得Δh=gt2,后一秒的位移总比前一秒的位移多10 m,所以前一秒内的平均速度总比后一秒的平均速度小10 m/s,故C正确,B错误;第7 s内的位移h=g×72-g×62=65 m,故D正确.
8.关于自由落体运动,下列说法中正确的是( ACD )
A.它是v0=0,加速度竖直向下且a=g的匀加速直线运动
B.在第1 s内、第2 s内、第3 s内的位移大小之比是1∶2∶3
C.在前1 s内、前2 s内、前3 s内的位移大小之比是1∶4∶9
D.在第1 s末、第2 s末、第3 s末的速度大小之比是1∶2∶3
解析:自由落体运动是初速度为零,加速度为g的竖直向下的匀加速直线运动,A正确;根据h=gt2,物体前1 s、前2 s、前3 s的位移之比为1∶4∶9,故第1 s内、第2 s内、第3 s内的位移大小之比是1∶3∶5,故B错误;根据h=gt2,物体前1 s、前2 s、前3 s的位移之比为1∶4∶9,故C正确;根据v=gt,在第1 s末、第2 s末、第3 s末的速度大小之比是1∶2∶3,故D正确.
三、非选择题
9.一位同学进行“用打点计时器测量自由落体加速度”的实验.
(1)现有下列器材可供选择:铁架台、电火花计时器及碳粉纸、电磁打点计时器及复写纸、纸带若干、220 V交流电源、低压直流电源、天平、停表、导线、开关.其中不必要的器材是:电磁打点计时器及复写纸、低压直流电源、天平、停表;缺少的器材是:毫米刻度尺、重锤.
(2)这位同学从打出的几条纸带中,挑出较为理想的一条纸带.把开始打的第一个点标为A,随后连续的几个点依次标记为点B、C、D、E和F,测量出各点间的距离,如图所示.请你在这位同学工作的基础上,思考求纸带加速度的方法,写出你所依据的公式:a=.
(3)由该纸带求出的自由落体加速度为9.56 m/s2;比标准值偏小(选填“偏大”或“偏小”).
(4)该实验误差的主要来源是空气的阻力和纸带的摩擦;可用增大重锤重力的方法减小该误差.
解析:(1)该实验中,要有做自由落体运动的物体——重锤,需要毫米刻度尺测量长度;通过打点计时器来记录物体运动时间,不需要停表和低压直流电源,不需要称量质量,因此不需要天平,不需要电磁打点计时器及复写纸,需要电火花计时器及碳粉纸、220 V交流电源.
(2)根据匀变速直线运动的推论公式Δx=aT2可以求出加速度的大小,所以所依据的公式为a=.
(3)设A、B之间的距离为x1,以后各段分别为x2、x3、x4、x5,
根据匀变速直线运动的推论公式Δx=aT2可以求出加速度的大小,则有
x3-x1=2a1T2
x4-x2=2a2T2
为了更加准确的求解加速度,我们对两个加速度取平均值
得:a=(a1+a2)
即自由落体加速度计算表达式为:
a= m/s2
≈9.56 m/s2
测量值比标准值偏小.
(4)该实验误差的主要来源是空气的阻力和纸带的摩擦;可用增大重锤重力的方法减小该误差.
10.一个物体从45 m高的地方自由下落,到达地面时的速度是多大?下落最后1 s内的位移是多大?(g取10 m/s2).
答案:30 m/s 25 m
解析:由v2=2gh得物体到达地面时的速度v== m/s=30 m/s.物体落地1 s前的速度v0=v-gt=30 m/s-10 m/s=20 m/s.故下落最后1 s内的位移h′=v0t+gt2=20×1 m+×10×12 m=25 m.
11.一矿井深为125 m,在井口每隔一定时间自由下落一个小球,当第11个小球从井口开始下落时,第1个小球恰好到达井底,求:
(1)相邻两个小球开始下落的时间间隔;
(2)这时第3个小球和第5个小球之间的距离.
答案:(1)0.5 s (2)35 m
解析:(1)设第一个小球下落到井底用时为t,根据自由落体运动位移时间关系h=gt2,则得t== s=5 s
设相邻小球下落时间间隔为T,
由题意知t=10T
联立解得T=0.5 s.
(2)由以上计算可知,当第一个小球到达井底时第三个小球刚好下落t1=4 s,第5个小球下落的时间为t2=3 s,故ΔH=H3-H5=g(t-t)=×10×(42-32) m=35 m.
12.一枚小火箭携带试验炸弹竖直发射升空,小火箭的加速度a=10 m/s2,t1=20 s后小火箭与试验炸弹分离,预定试验炸弹在最高点爆炸,取g=10 m/s2,不计空气阻力.
(1)试验炸弹预定爆炸点的高度是多少?
(2)若试验失败,炸弹未爆炸,如果不采取措施,炸弹会在分离后多长时间落地?为了防止危险,在炸弹到达最高点10 s后,以v0=400 m/s竖直发射一枚炮弹拦截,拦截点的高度是多少?
答案:(1)4 000 m (2)20(+1) s 2 555 m
解析:(1)试验炸弹与小火箭分离时,速度v1=at1=10×20 m/s=200 m/s,高度h1=at=×10×202 m=2 000 m,分离后炸弹以初速度v1做竖直上抛运动,上升高度h2===2 000 m,故预定爆炸点的高度h=h1+h2=4 000 m.
(2)如果不采取措施,从分离到炸弹落地,上升阶段的时间t上== s=20 s,下降阶段有h=gt,得t下==20 s,故从分离到落地所用时间t3=t上+t下=20(+1) s,发射炮弹时,炸弹下落高度h3=gt=×10×102 m=500 m,此时离地高度h4=h-h3=3 500 m,下落速度v3=gt2=10×10 m/s=100 m/s,到两者相遇时,其位移的大小之和等于h4,故v3t+gt2+v0t-gt2=h4,代入数据t=7 s,故拦截点高度h5=v0t-gt2=400×7 m-×10×72 m=2 555 m.
1.从同一高度做自由落体运动的甲、乙两个小铁球,甲的质量是乙的两倍,则( D )
A.甲比乙先落地,落地时甲的速度是乙的两倍
B.甲比乙先落地,落地时甲、乙的速度相同
C.甲、乙同时落地,落地时甲的速度是乙的两倍
D.甲、乙同时落地,落地时甲、乙的速度相同
解析:根据自由落体运动的公式h=gt2,t=,知落地时间与质量无关,所以两个物体同时落地.故D正确,A、B、C均错误.
2.已知广州地区的重力加速度为9.8 m/s2,在此地区物体做自由落体运动的说法中,正确的是( A )
A.下落过程,物体的速度每秒增加9.8 m/s
B.自由落体运动是一种匀速运动
C.释放物体瞬间,物体速度和加速度都为零
D.物体越重,下落的越快
解析:重力加速度为9.8 m/s2,故自由下落过程中物体的速度每秒增加9.8 m/s,故A正确;自由落体运动是初速度为零,加速度为g的匀加速直线运动,故B错误;释放物体瞬间,物体速度为零,加速度为g,故C错误;重力加速度与物体的质量无关,重物与轻物下落一样快,故D错误.
3.如图所示,A、B两小球用长为L的细线连接悬挂在空中.A距湖水水面高度为H,释放小球,让它们自由落下,测得它们落水声相差Δt.如果球A距湖面的高度H减小,则Δt将( A )
A.增大 B.不变
C.减小 D.无法判断
解析:此题应用v-t图象分析,作出A、B的v-t图象,如图所示.若释放高度H2>H1,则当B球落到水面时,两种情况下B对应的速度分别为v2、v1.由图看出v2>v1,此后A球做匀加速直线运动,两种情况A对应的速度分别为v′2、v′1,加速度均为g,已知两种情况下A球与B球落至水面的位移差相同,所以图示的两个阴影梯形面积大小相等,则Δt1>Δt2,选项A正确.
4.跳伞运动员以5 m/s的速度匀速下降,在距地面10 m处掉了一颗扣子,跳伞运动员比扣子晚着地的时间为(不计空气阻力对扣子的作用,g取10 m/s2)( A )
A.1 s B.2 s
C. s D.(2-) s
解析:设扣子着陆的时间为t1,则:h=v0t1+gt,代入数据解得t1=1 s.设跳伞运动员着陆时间为t2,则:h=v0t2,解得:t2=2 s,而Δt=t2-t1=1 s.故A正确,B、C、D错误.
5.取一根长2 m左右的细线,5个铁垫圈和一个金属盘.在线端系上第一个垫圈,隔12 cm再系一个,以后垫圈之间的距离分别为36 cm、60 cm、84 cm,如图所示.站在椅子上,向上提起线的上端,让线自由垂下,且第一个垫圈紧靠放在地上的金属盘.松手后开始计时,若不计空气阻力,则第2、3、4、5各垫圈( B )
A.落到盘上的声音时间间隔越来越大
B.落到盘上的声音时间间隔相等
C.依次落到盘上的速率关系为1∶∶∶2
D.依次落到盘上的时间关系为1∶(-1)∶(-)∶(2-)
解析:4个铁垫圈同时做自由落体运动,下降的位移之比为1∶3∶5∶7.可以看成一个铁垫圈自由下落,经过位移之比为1∶3∶5∶7.因为初速度为零的匀加速直线运动在相等时间内的位移之比为1∶3∶5∶7,知各垫圈落到盘中的时间间隔相等,故A错误,B正确.因为各垫圈落到盘中的时间间隔相等,则各垫圈依次落到盘中的时间比为1∶2∶3∶4,根据v=gt可知,速率之比为1∶2∶3∶4,故C、D错误.
二、多项选择题
6.一物体从一行星表面某高度处自由下落(不计表层大气阻力).自开始下落计时,得到物体离该行星表面的高度h随时间t变化的图象如图所示,则( AC )
A.行星表面重力加速度大小为8 m/s2
B.行星表面重力加速度大小为10 m/s2
C.物体落到行星表面时的速度大小为20 m/s
D.物体落到行星表面时的速度大小为25 m/s
解析:由图中可以看出物体从h=25 m处开始下落,在空中运动了t=2.5 s到达行星表面,根据h=at2,可以求出a=8 m/s2,故A正确;根据运动学公式可以算出v=at=20 m/s,可知C正确.
7.某物体做自由落体运动(g=10 m/s2),则( ACD )
A.第2 s内的平均速度为15 m/s
B.后一秒的位移总比前一秒的位移多5 m
C.前一秒的平均速度总比后一秒的平均速度小10 m/s
D.第7 s内的位移为65 m
解析:第2 s内的位移为h=g×22-g×12=15 m,所以第2 s内的平均速度为v== m/s=15 m/s,A正确;根据逐差法可得Δh=gt2,后一秒的位移总比前一秒的位移多10 m,所以前一秒内的平均速度总比后一秒的平均速度小10 m/s,故C正确,B错误;第7 s内的位移h=g×72-g×62=65 m,故D正确.
8.关于自由落体运动,下列说法中正确的是( ACD )
A.它是v0=0,加速度竖直向下且a=g的匀加速直线运动
B.在第1 s内、第2 s内、第3 s内的位移大小之比是1∶2∶3
C.在前1 s内、前2 s内、前3 s内的位移大小之比是1∶4∶9
D.在第1 s末、第2 s末、第3 s末的速度大小之比是1∶2∶3
解析:自由落体运动是初速度为零,加速度为g的竖直向下的匀加速直线运动,A正确;根据h=gt2,物体前1 s、前2 s、前3 s的位移之比为1∶4∶9,故第1 s内、第2 s内、第3 s内的位移大小之比是1∶3∶5,故B错误;根据h=gt2,物体前1 s、前2 s、前3 s的位移之比为1∶4∶9,故C正确;根据v=gt,在第1 s末、第2 s末、第3 s末的速度大小之比是1∶2∶3,故D正确.
三、非选择题
9.一位同学进行“用打点计时器测量自由落体加速度”的实验.
(1)现有下列器材可供选择:铁架台、电火花计时器及碳粉纸、电磁打点计时器及复写纸、纸带若干、220 V交流电源、低压直流电源、天平、停表、导线、开关.其中不必要的器材是:电磁打点计时器及复写纸、低压直流电源、天平、停表;缺少的器材是:毫米刻度尺、重锤.
(2)这位同学从打出的几条纸带中,挑出较为理想的一条纸带.把开始打的第一个点标为A,随后连续的几个点依次标记为点B、C、D、E和F,测量出各点间的距离,如图所示.请你在这位同学工作的基础上,思考求纸带加速度的方法,写出你所依据的公式:a=.
(3)由该纸带求出的自由落体加速度为9.56 m/s2;比标准值偏小(选填“偏大”或“偏小”).
(4)该实验误差的主要来源是空气的阻力和纸带的摩擦;可用增大重锤重力的方法减小该误差.
解析:(1)该实验中,要有做自由落体运动的物体——重锤,需要毫米刻度尺测量长度;通过打点计时器来记录物体运动时间,不需要停表和低压直流电源,不需要称量质量,因此不需要天平,不需要电磁打点计时器及复写纸,需要电火花计时器及碳粉纸、220 V交流电源.
(2)根据匀变速直线运动的推论公式Δx=aT2可以求出加速度的大小,所以所依据的公式为a=.
(3)设A、B之间的距离为x1,以后各段分别为x2、x3、x4、x5,
根据匀变速直线运动的推论公式Δx=aT2可以求出加速度的大小,则有
x3-x1=2a1T2
x4-x2=2a2T2
为了更加准确的求解加速度,我们对两个加速度取平均值
得:a=(a1+a2)
即自由落体加速度计算表达式为:
a= m/s2
≈9.56 m/s2
测量值比标准值偏小.
(4)该实验误差的主要来源是空气的阻力和纸带的摩擦;可用增大重锤重力的方法减小该误差.
10.一个物体从45 m高的地方自由下落,到达地面时的速度是多大?下落最后1 s内的位移是多大?(g取10 m/s2).
答案:30 m/s 25 m
解析:由v2=2gh得物体到达地面时的速度v== m/s=30 m/s.物体落地1 s前的速度v0=v-gt=30 m/s-10 m/s=20 m/s.故下落最后1 s内的位移h′=v0t+gt2=20×1 m+×10×12 m=25 m.
11.一矿井深为125 m,在井口每隔一定时间自由下落一个小球,当第11个小球从井口开始下落时,第1个小球恰好到达井底,求:
(1)相邻两个小球开始下落的时间间隔;
(2)这时第3个小球和第5个小球之间的距离.
答案:(1)0.5 s (2)35 m
解析:(1)设第一个小球下落到井底用时为t,根据自由落体运动位移时间关系h=gt2,则得t== s=5 s
设相邻小球下落时间间隔为T,
由题意知t=10T
联立解得T=0.5 s.
(2)由以上计算可知,当第一个小球到达井底时第三个小球刚好下落t1=4 s,第5个小球下落的时间为t2=3 s,故ΔH=H3-H5=g(t-t)=×10×(42-32) m=35 m.
12.一枚小火箭携带试验炸弹竖直发射升空,小火箭的加速度a=10 m/s2,t1=20 s后小火箭与试验炸弹分离,预定试验炸弹在最高点爆炸,取g=10 m/s2,不计空气阻力.
(1)试验炸弹预定爆炸点的高度是多少?
(2)若试验失败,炸弹未爆炸,如果不采取措施,炸弹会在分离后多长时间落地?为了防止危险,在炸弹到达最高点10 s后,以v0=400 m/s竖直发射一枚炮弹拦截,拦截点的高度是多少?
答案:(1)4 000 m (2)20(+1) s 2 555 m
解析:(1)试验炸弹与小火箭分离时,速度v1=at1=10×20 m/s=200 m/s,高度h1=at=×10×202 m=2 000 m,分离后炸弹以初速度v1做竖直上抛运动,上升高度h2===2 000 m,故预定爆炸点的高度h=h1+h2=4 000 m.
(2)如果不采取措施,从分离到炸弹落地,上升阶段的时间t上== s=20 s,下降阶段有h=gt,得t下==20 s,故从分离到落地所用时间t3=t上+t下=20(+1) s,发射炮弹时,炸弹下落高度h3=gt=×10×102 m=500 m,此时离地高度h4=h-h3=3 500 m,下落速度v3=gt2=10×10 m/s=100 m/s,到两者相遇时,其位移的大小之和等于h4,故v3t+gt2+v0t-gt2=h4,代入数据t=7 s,故拦截点高度h5=v0t-gt2=400×7 m-×10×72 m=2 555 m.
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
