人教版八年级上册数学 12.3 角平分线的性质 同步测试(Word版 含解析)
文档属性
| 名称 | 人教版八年级上册数学 12.3 角平分线的性质 同步测试(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 155.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 00:00:00 | ||
图片预览




文档简介
12.3
角平分线的性质
同步测试
一.选择题
1.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D.若AD=2,则点D到BC的距离为( )
A.1
B.
C.
D.2
2.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为( )
A.6
B.5
C.4
D.3
3.如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是( )
A.线段CD的中点
B.CD与过点O作CD的垂线的交点
C.CD与∠AOB的平分线的交点
D.以上均不对
4.已知EF是△EBC的角平分线,FD⊥EB于D,且FD=3cm,则点F到EC的距离是( )
A.2cm
B.3cm
C.4cm
D.6cm
5.如图,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为( )
A.3
B.10
C.12
D.15
6.如图,已知点P到△ABC三边的距离相等,DE∥AC,AB=8.1cm,BC=6cm,△BDE的周长为( )cm.
A.12
B.14.1
C.16.2
D.7.05
7.如图,BD是△ABC的角平分线,DE⊥AB,垂足为E,AB=6,BC=4,DE=2,则△ABC的面积为( )
A.4
B.6
C.8
D.10
8.如图,AD是△ABC的角平分线,DE⊥AB,AB=6cm,DE=4cm,S△ABC=30cm2,则AC的长为( )
A.10cm
B.9cm
C.4.5cm
D.3cm
9.如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,若点P到直线AC的距离为4,则点P到直线AB的距离为( )
A.4
B.3
C.2
D.1
10.如图,∠AOB=150°,OC平分∠AOB,P为OC上一点,PD∥OA交OB于点D,PE⊥OA于点E.若OD=4,则PE的长为( )
A.2
B.2.5
C.3
D.4
二.填空题
11.如图,在Rt△ABC中,∠C=90°,AB=16,AD平分∠BAC交BC于点D,若CD=4,则△ABD的面积为
.
12.如图,BD平分∠ABC交AC于点D,DE⊥BC于点E,若AB=5,BC=7,S△ABC=12,则DE的长为
.
13.如图,在△ABC中,CD平分∠ACB交AB于D,DE∥BC交AC于E,若∠ACB=60°,则∠EDC=
.
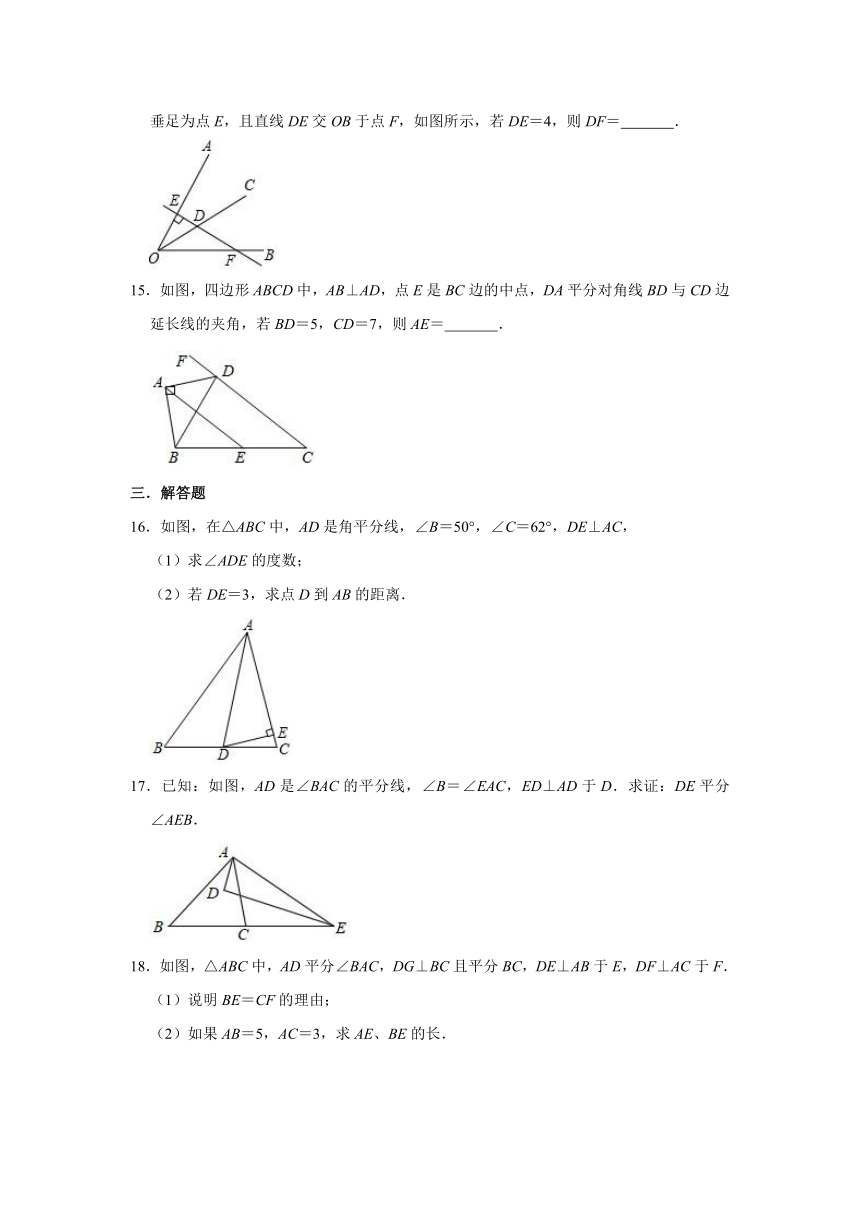
14.已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F,如图所示,若DE=4,则DF=
.
15.如图,四边形ABCD中,AB⊥AD,点E是BC边的中点,DA平分对角线BD与CD边延长线的夹角,若BD=5,CD=7,则AE=
.
三.解答题
16.如图,在△ABC中,AD是角平分线,∠B=50°,∠C=62°,DE⊥AC,
(1)求∠ADE的度数;
(2)若DE=3,求点D到AB的距离.
17.已知:如图,AD是∠BAC的平分线,∠B=∠EAC,ED⊥AD于D.求证:DE平分∠AEB.
18.如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)说明BE=CF的理由;
(2)如果AB=5,AC=3,求AE、BE的长.
参考答案
1.解:过点D作DE⊥BC于E,
∵BD平分∠ABC,∠A=90°,DE⊥BC,
∴DE=AD=2,
故选:D.
2.解:∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DC=DE=4,
∴BD=BC﹣CD=9﹣4=5.
故选:B.
3.解:∵点P到边OA,OB的距离相等,
∴点P在∠AOB的平分线上,
∴点P为CD与∠AOB的平分线的交点.
故选:C.
4.解:∵FD⊥EB于D,且FD=3cm,
∴点F到EB的距离为3cm,
∵EF是△EBC的角平分线,
∴点F到EB和EC的距离相等,
∴点F到EC的距离是3cm.
故选:B.
5.解:作DE⊥AB于E.
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DE=CD=3.
∴△ABD的面积为×3×10=15.
故选:D.
6.解:∵点P到△ABC三边的距离相等,
∴AP平分∠BAC,
∴∠DAP=∠CAP,
∵DE∥AC,
∴∠DPA=∠PAC,
∴∠DAP=∠APD,
∴AD=PD,
同理PE=CE,
∴△BDE的周BD+DE+BE=BD+PD+PE+BE=BD+AD+BE+CE=AB+BC=14.1cm,
故选:B.
7.解:作DF⊥BC于F,如图,
∵BD是△ABC的角平分线,DE⊥AB,DF⊥BC,
∴DF=DE=2,
∴S△ABC=S△ABD+S△BCD
=×6×2+×4×2
=10.
故选:D.
8.解:过点D作DF⊥AC于F,
∵AD是△ABC的角平分线,DE⊥AB,
∴DE=DF=4,
∵AB=6,
∴S△ABC=×6×4+AC×4=30,
解得AC=9;
故选:B.
9.解:如图,过点P作PF⊥AC于F,作PG⊥BC于G,PH⊥AB于H,
∵BD、CE是△ABC的外角平分线,
∴PF=PG,PG=PH,
∴PF=PG=PH,
∵点P到AC的距离为4,
∴PH=4,
即点P到AB的距离为4.
故选:A.
10.解:过P点作PF⊥OD,
∵∠AOB=150°,OC平分∠AOB,
∴∠DOP=∠POE=75°,
∵DP∥OA,
∴∠DPO=∠POE=75°,
∴∠DOP=∠DPO﹣75°,
∴DP=OD=4,
∴∠PDO=180°﹣75°﹣75°=30°,
∵PF⊥OD,
∴∠PFD=90°,
∴PF=DP=2,
∵PE⊥OA,OC平分∠AOB,
∴PE=PF=2,
故选:A.
11.解:作DE⊥AB于E,
∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴DE=DC=4,
∴△ABD的面积=×AB×DE=32,
故答案为:32.
12.解:作DF⊥AB于F,
∵BD平分∠ABC,DE⊥BC,DF⊥AB,
∴DE=DF,
∴×AB×DF+×BC×DE=S△ABC,即×5×DE+×7×DE=12,
解得,DE=2,
故答案为:2.
13.解:如图,在△ABC中,CD平分∠ACB交AB于D,∠ACB=60°,
∴∠BCD=∠DCE=∠ACB=30°.
又∵DE∥BC,
∴∠EDC=∠BCD=30°.
故答案是:30°.
14.解:作DG⊥OB于G,
∵OC是∠AOB的平分线,DG⊥OB,DE⊥OA,
∴DG=DE=4,
在Rt△EOF中,∠AOB=60°,
∴∠OFE=30°,
∴DF=2DG=8,
故答案为:8.
15.解:如图,
取BD中点H,连AH、EH,
∵AB⊥AD,
∴AH=DH=BH=BD=2.5,
∴∠HDA=∠HAD,
∵DA平分∠FDB,
∴∠FDA=∠HDA,
∴∠FDA=∠HAD,
∴AH∥DF,
∵点E是BC边的中点,点H是BD的中点,
∴EH∥CD,EH=CD=3.5,
∴A、H、E三点共线,
∴AE=AH+EH=2.5+3.5=6.
故答案为:6.
16.解:(1)∵∠B=50°,∠C=62°,
∴∠BAC=180°﹣50°﹣62°=68°,
∵AD是角平分线,
∴∠DAC=∠BAC=34°,
∵DE⊥AC,
∴∠AED=90°,
∴∠ADE=90°﹣34°=56°;
(2)作DF⊥AB于F,如图,
∵AD是角平分线,DF⊥AB,DE⊥AC,
∴DF=DE=3,
即点D到AB的距离为3.
17.证明:延长AD交BC于F,
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD,
∵∠DFE=∠B+∠BAD,∠DAE=∠EAC+∠CAD,
∵∠B=∠EAC,
∴∠DFE=∠DAE,
∴AE=FE,
∵ED⊥AD,
∴ED平分∠AEB.
18.(1)证明:连接BD,CD,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
∵DG⊥BC且平分BC,
∴BD=CD,
在Rt△BED与Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)解:在△AED和△AFD中,
,
∴△AED≌△AFD(AAS),
∴AE=AF,
设BE=x,则CF=x,
∵AB=5,AC=3,AE=AB﹣BE,AF=AC+CF,
∴5﹣x=3+x,
解得:x=1,
∴BE=1,AE=AB﹣BE=5﹣1=4.
角平分线的性质
同步测试
一.选择题
1.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D.若AD=2,则点D到BC的距离为( )
A.1
B.
C.
D.2
2.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为( )
A.6
B.5
C.4
D.3
3.如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是( )
A.线段CD的中点
B.CD与过点O作CD的垂线的交点
C.CD与∠AOB的平分线的交点
D.以上均不对
4.已知EF是△EBC的角平分线,FD⊥EB于D,且FD=3cm,则点F到EC的距离是( )
A.2cm
B.3cm
C.4cm
D.6cm
5.如图,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为( )
A.3
B.10
C.12
D.15
6.如图,已知点P到△ABC三边的距离相等,DE∥AC,AB=8.1cm,BC=6cm,△BDE的周长为( )cm.
A.12
B.14.1
C.16.2
D.7.05
7.如图,BD是△ABC的角平分线,DE⊥AB,垂足为E,AB=6,BC=4,DE=2,则△ABC的面积为( )
A.4
B.6
C.8
D.10
8.如图,AD是△ABC的角平分线,DE⊥AB,AB=6cm,DE=4cm,S△ABC=30cm2,则AC的长为( )
A.10cm
B.9cm
C.4.5cm
D.3cm
9.如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,若点P到直线AC的距离为4,则点P到直线AB的距离为( )
A.4
B.3
C.2
D.1
10.如图,∠AOB=150°,OC平分∠AOB,P为OC上一点,PD∥OA交OB于点D,PE⊥OA于点E.若OD=4,则PE的长为( )
A.2
B.2.5
C.3
D.4
二.填空题
11.如图,在Rt△ABC中,∠C=90°,AB=16,AD平分∠BAC交BC于点D,若CD=4,则△ABD的面积为
.
12.如图,BD平分∠ABC交AC于点D,DE⊥BC于点E,若AB=5,BC=7,S△ABC=12,则DE的长为
.
13.如图,在△ABC中,CD平分∠ACB交AB于D,DE∥BC交AC于E,若∠ACB=60°,则∠EDC=
.
14.已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F,如图所示,若DE=4,则DF=
.
15.如图,四边形ABCD中,AB⊥AD,点E是BC边的中点,DA平分对角线BD与CD边延长线的夹角,若BD=5,CD=7,则AE=
.
三.解答题
16.如图,在△ABC中,AD是角平分线,∠B=50°,∠C=62°,DE⊥AC,
(1)求∠ADE的度数;
(2)若DE=3,求点D到AB的距离.
17.已知:如图,AD是∠BAC的平分线,∠B=∠EAC,ED⊥AD于D.求证:DE平分∠AEB.
18.如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)说明BE=CF的理由;
(2)如果AB=5,AC=3,求AE、BE的长.
参考答案
1.解:过点D作DE⊥BC于E,
∵BD平分∠ABC,∠A=90°,DE⊥BC,
∴DE=AD=2,
故选:D.
2.解:∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DC=DE=4,
∴BD=BC﹣CD=9﹣4=5.
故选:B.
3.解:∵点P到边OA,OB的距离相等,
∴点P在∠AOB的平分线上,
∴点P为CD与∠AOB的平分线的交点.
故选:C.
4.解:∵FD⊥EB于D,且FD=3cm,
∴点F到EB的距离为3cm,
∵EF是△EBC的角平分线,
∴点F到EB和EC的距离相等,
∴点F到EC的距离是3cm.
故选:B.
5.解:作DE⊥AB于E.
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DE=CD=3.
∴△ABD的面积为×3×10=15.
故选:D.
6.解:∵点P到△ABC三边的距离相等,
∴AP平分∠BAC,
∴∠DAP=∠CAP,
∵DE∥AC,
∴∠DPA=∠PAC,
∴∠DAP=∠APD,
∴AD=PD,
同理PE=CE,
∴△BDE的周BD+DE+BE=BD+PD+PE+BE=BD+AD+BE+CE=AB+BC=14.1cm,
故选:B.
7.解:作DF⊥BC于F,如图,
∵BD是△ABC的角平分线,DE⊥AB,DF⊥BC,
∴DF=DE=2,
∴S△ABC=S△ABD+S△BCD
=×6×2+×4×2
=10.
故选:D.
8.解:过点D作DF⊥AC于F,
∵AD是△ABC的角平分线,DE⊥AB,
∴DE=DF=4,
∵AB=6,
∴S△ABC=×6×4+AC×4=30,
解得AC=9;
故选:B.
9.解:如图,过点P作PF⊥AC于F,作PG⊥BC于G,PH⊥AB于H,
∵BD、CE是△ABC的外角平分线,
∴PF=PG,PG=PH,
∴PF=PG=PH,
∵点P到AC的距离为4,
∴PH=4,
即点P到AB的距离为4.
故选:A.
10.解:过P点作PF⊥OD,
∵∠AOB=150°,OC平分∠AOB,
∴∠DOP=∠POE=75°,
∵DP∥OA,
∴∠DPO=∠POE=75°,
∴∠DOP=∠DPO﹣75°,
∴DP=OD=4,
∴∠PDO=180°﹣75°﹣75°=30°,
∵PF⊥OD,
∴∠PFD=90°,
∴PF=DP=2,
∵PE⊥OA,OC平分∠AOB,
∴PE=PF=2,
故选:A.
11.解:作DE⊥AB于E,
∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴DE=DC=4,
∴△ABD的面积=×AB×DE=32,
故答案为:32.
12.解:作DF⊥AB于F,
∵BD平分∠ABC,DE⊥BC,DF⊥AB,
∴DE=DF,
∴×AB×DF+×BC×DE=S△ABC,即×5×DE+×7×DE=12,
解得,DE=2,
故答案为:2.
13.解:如图,在△ABC中,CD平分∠ACB交AB于D,∠ACB=60°,
∴∠BCD=∠DCE=∠ACB=30°.
又∵DE∥BC,
∴∠EDC=∠BCD=30°.
故答案是:30°.
14.解:作DG⊥OB于G,
∵OC是∠AOB的平分线,DG⊥OB,DE⊥OA,
∴DG=DE=4,
在Rt△EOF中,∠AOB=60°,
∴∠OFE=30°,
∴DF=2DG=8,
故答案为:8.
15.解:如图,
取BD中点H,连AH、EH,
∵AB⊥AD,
∴AH=DH=BH=BD=2.5,
∴∠HDA=∠HAD,
∵DA平分∠FDB,
∴∠FDA=∠HDA,
∴∠FDA=∠HAD,
∴AH∥DF,
∵点E是BC边的中点,点H是BD的中点,
∴EH∥CD,EH=CD=3.5,
∴A、H、E三点共线,
∴AE=AH+EH=2.5+3.5=6.
故答案为:6.
16.解:(1)∵∠B=50°,∠C=62°,
∴∠BAC=180°﹣50°﹣62°=68°,
∵AD是角平分线,
∴∠DAC=∠BAC=34°,
∵DE⊥AC,
∴∠AED=90°,
∴∠ADE=90°﹣34°=56°;
(2)作DF⊥AB于F,如图,
∵AD是角平分线,DF⊥AB,DE⊥AC,
∴DF=DE=3,
即点D到AB的距离为3.
17.证明:延长AD交BC于F,
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD,
∵∠DFE=∠B+∠BAD,∠DAE=∠EAC+∠CAD,
∵∠B=∠EAC,
∴∠DFE=∠DAE,
∴AE=FE,
∵ED⊥AD,
∴ED平分∠AEB.
18.(1)证明:连接BD,CD,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
∵DG⊥BC且平分BC,
∴BD=CD,
在Rt△BED与Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)解:在△AED和△AFD中,
,
∴△AED≌△AFD(AAS),
∴AE=AF,
设BE=x,则CF=x,
∵AB=5,AC=3,AE=AB﹣BE,AF=AC+CF,
∴5﹣x=3+x,
解得:x=1,
∴BE=1,AE=AB﹣BE=5﹣1=4.
