第三章 位置与坐标 单元测试题(含答案)
文档属性
| 名称 | 第三章 位置与坐标 单元测试题(含答案) |  | |
| 格式 | rar | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 14:03:42 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师版八年级上学期第三章单元检测试题
本试卷总分120分,考试时间100分钟
一、单选题(共12题;共36分)
1.若点M(m+3,m﹣2)在x轴上,则点M的坐标为(??? )
A.?(0,﹣5)????????????????????????B.?(0,5)????????????????????????C.?(﹣5,0)????????????????????????D.?(5,0)
2.已知直线 轴,A点的坐标为 ,并且线段 ,则点B的坐标为(??? )
A.???????????????????????B.???????????????????????C.? 或 ??????????????????????D.? 或
3.在平面直角坐标系中,将点 向右平移3个单位得到点 ,则点 关于x轴的对称点的坐标为(??? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
4.如图是小刚画的一张脸,如果用(0,2)表示A点所在的眼睛,用(2,2)表示B点所在的眼睛,那么C点表示的嘴的位置可以表示成(??? )
A.?(1,0)???????????????????????????????B.?(-1,0)???????????????????????????????
C.?(-1,1)?????????????????????????????D.?(1,-1)
5.点P的横坐标是-3,且到x轴的距离为5,则P点的坐标是(??? )
A.? 或 ??????????????B.? 或 ??????????????C.???????????????D.?
6.在平面直角坐标系中,点A的坐标是(3a﹣5,a+1).若点A到x轴的距离与到y轴的距离相等,且点A在y轴的右侧,则a的值为(? )
A.?1?????????????????????????????????????????B.?2?????????????????????????????????????????C.?3?????????????????????????????????????????D.?1 或 3
7.如图,弹性小球从点P(0,1)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到正方形的边时的点为P1(﹣2,0),第2次碰到正方形的边时的点为P2 , …,第n次碰到正方形的边时的点为Pn , 则点P2020的坐标是(?? )
A.?(0,1)????????????????????????B.?(﹣2,4)????????????????????????
C.?(﹣2,0)???????????????????D.?(0,3)
8.如图,平面直角坐标系内有一条折线从原点出发后,在第一象限内曲折前行,已知A1A2⊥OA1 , A1A2=OA1; A2A3⊥A1A2 , A2A3=A1A2;A3A4⊥A2A3 , A3A4=A2A3;……;依照这个规律进行下去,其中A1(1,2),A2(3,1),A3(4,3),……. ,则A2019的坐标是(? )
A.?(2019,2020)??????????B.?( 2019,2018)??????????C.?(3027,1009)??????????D.?(3028,1011)
9.在平面直角坐标系中,点 关于 轴对称的点的坐标为(??? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
10.如图,在平面直角坐标系中,菱形ABCD的顶点A在y轴上,已知B(﹣3,0)、C(2,0),则点D的坐标为(?? )
A.?(4,5)???????????????????????????B.?(5,4)?????????????????????????
?
?C.?(5,3)???????????????????????????D.?(4,3)
11.已知点A(2x﹣4,x+2)在坐标轴上,则x的值等于(?? )
A.?2或﹣2???????????????????B.?﹣2??????????????????????????????????C.?2??????????????????????????????????D.?非上述答案
12.如图,已知三角形ABC如图所示放置在平面直角坐标系中,其中C(-4,4).则三角形ABC 的面积是(?? )
? A.?4??????????????????????????????????????????B.?6????????????????????????????????????????
?C.?12????????????????????????????????????????D.?24
二、填空题(共6题;共24分)
13.以水平数轴的原点 为圆心过正半轴 上的每一刻度点画同心圆,将 逆时针依次旋转 、 、 、 、 得到 条射线,构成如图所示的“圆”坐标系,点 、 的坐标分别表示为 、 ,则点 的坐标表示为________.
14.已知点P(﹣2,1),则点P关于x轴对称的点的坐标是________.
15.平面直角坐标系中,将点A(﹣1,2)先向左平移2个单位,再向上平移1个单位后得到的点A1的坐标为________.
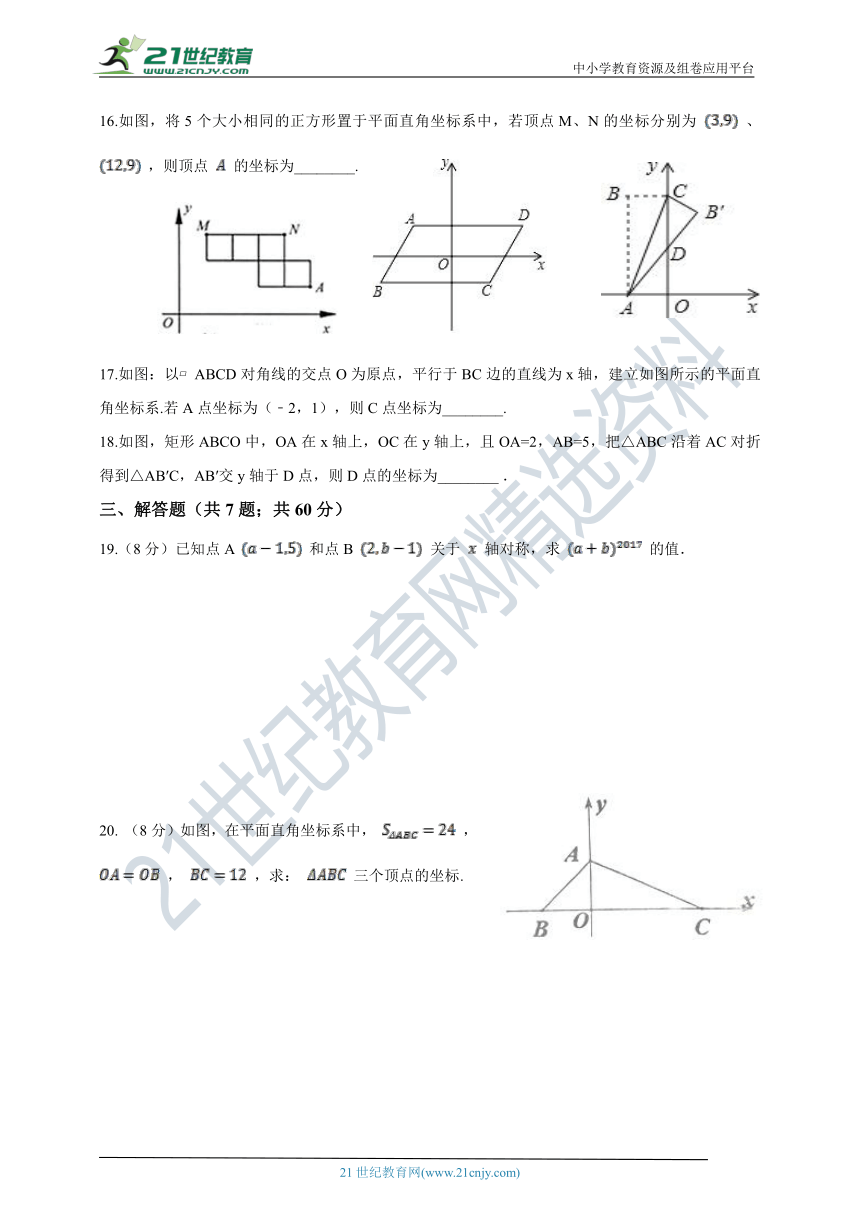
16.如图,将5个大小相同的正方形置于平面直角坐标系中,若顶点M、N的坐标分别为 、 ,则顶点 的坐标为________.
17.如图:以?ABCD对角线的交点O为原点,平行于BC边的直线为x轴,建立如图所示的平面直角坐标系.若A点坐标为(﹣2,1),则C点坐标为________.
18.如图,矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则D点的坐标为________?.
三、解答题(共7题;共60分)
19.(8分)已知点A 和点B 关于 轴对称,求 的值.
20. (8分)如图,在平面直角坐标系中, , , ,求: 三个顶点的坐标.
21. (8分)已知:点A、B在平面直角坐标系中的位置如图所示,求△AOB的面积.
22. (8分)如果B(m+1,3m﹣5)到x轴的距离与它到y轴的距离相等,求:
(1)m的值;
(2)求它关于原点的对称点坐标.
23.如图,已知四边形ABCD,则四边形ABCD的面积是多少?
24. (8分)如图,已知 ,点 分别在 轴正半轴和 轴正半轴上, ,试求 的值.
25. (12分)如图,用(-1,0)表示A点的位置,用(2,1)表示B点的位置,那么:
(1)画出直角坐标系。
(2)写出△DEF的三个顶点的坐标。
(3)在图中表示出点M(6,2),N(4,4)的位置。
答案解析部分
一、单选题
1.【答案】 D
2.【答案】 D
3.【答案】 A
4.【答案】 A
5.【答案】 B
6.【答案】 C
7.【答案】 B
8.【答案】 D
9.【答案】 D
10.【答案】 B
11.【答案】 A
12.【答案】 C
二、填空题
13.【答案】 (3,240°)
14.【答案】(﹣2,﹣1)
15.【答案】 (﹣3,3)
16.【答案】 (15,3)
17.【答案】 (2,﹣1)
18.【答案】 (0,2.1)
三、解答题
19.【答案】解:∵点A ,点B 关于 轴对称,
∴ ,解得
∴
20.【答案】 根据题意有:
解答:
???
、 、
21.【答案】 设AB交x轴于C,那么根据图中的信息可知: OC=1, S△OAC= ×1×2=1, S△OBC= ×1×2=1, 因此S△OAB=S△OAC+S△OBC=2.
22.【答案】 (1)解:由题意得:m+1=3m﹣5,或m+1+3m﹣5=0,
解得:m=3或m=1
(2)解:当m=3时,B(4,4)关于原点的对称点坐标(﹣4,﹣4);
当m=1时,B(2,﹣2)关于原点的对称点坐标(﹣2,2)
23.【答案】 解:过点B作BE⊥x轴于点E,如下图所示:
四边形ABCD分成△AOD,梯形BEOA,△BCE,
S△AOD= ×OD×OA= ×1×4=2,
S梯形BEOA= ×(BE+OA)×OE= ×(3+4)×3= ,
S△BCE= ×CE×BE= ×2×3=3,
S四边形ABCD=2+ +3=15.5,
即四边形ABCD的面积为15.5.
24.【答案】 解:过 作 轴于 轴于,
,
,
轴 轴,
,
,
则四边形 是正方形,
,
,
,
,
在 和 中
,
,
,
故答案为: .
25.【答案】 (1)解:以O点为原点,水平向右为正方向画x轴,垂直往上为正方向画y轴,依此建立直角坐标系即可
(2)解:根据(1)建立的直角坐标系,D(1,2),E(4,3),F(0,4)
(3)解:在(1)建立的直角坐标系标记出点M(6,2)、N(4,4)的位置.
_21?????????è?????(www.21cnjy.com)_
北师版八年级上学期第三章单元检测试题
本试卷总分120分,考试时间100分钟
一、单选题(共12题;共36分)
1.若点M(m+3,m﹣2)在x轴上,则点M的坐标为(??? )
A.?(0,﹣5)????????????????????????B.?(0,5)????????????????????????C.?(﹣5,0)????????????????????????D.?(5,0)
2.已知直线 轴,A点的坐标为 ,并且线段 ,则点B的坐标为(??? )
A.???????????????????????B.???????????????????????C.? 或 ??????????????????????D.? 或
3.在平面直角坐标系中,将点 向右平移3个单位得到点 ,则点 关于x轴的对称点的坐标为(??? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
4.如图是小刚画的一张脸,如果用(0,2)表示A点所在的眼睛,用(2,2)表示B点所在的眼睛,那么C点表示的嘴的位置可以表示成(??? )
A.?(1,0)???????????????????????????????B.?(-1,0)???????????????????????????????
C.?(-1,1)?????????????????????????????D.?(1,-1)
5.点P的横坐标是-3,且到x轴的距离为5,则P点的坐标是(??? )
A.? 或 ??????????????B.? 或 ??????????????C.???????????????D.?
6.在平面直角坐标系中,点A的坐标是(3a﹣5,a+1).若点A到x轴的距离与到y轴的距离相等,且点A在y轴的右侧,则a的值为(? )
A.?1?????????????????????????????????????????B.?2?????????????????????????????????????????C.?3?????????????????????????????????????????D.?1 或 3
7.如图,弹性小球从点P(0,1)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到正方形的边时的点为P1(﹣2,0),第2次碰到正方形的边时的点为P2 , …,第n次碰到正方形的边时的点为Pn , 则点P2020的坐标是(?? )
A.?(0,1)????????????????????????B.?(﹣2,4)????????????????????????
C.?(﹣2,0)???????????????????D.?(0,3)
8.如图,平面直角坐标系内有一条折线从原点出发后,在第一象限内曲折前行,已知A1A2⊥OA1 , A1A2=OA1; A2A3⊥A1A2 , A2A3=A1A2;A3A4⊥A2A3 , A3A4=A2A3;……;依照这个规律进行下去,其中A1(1,2),A2(3,1),A3(4,3),……. ,则A2019的坐标是(? )
A.?(2019,2020)??????????B.?( 2019,2018)??????????C.?(3027,1009)??????????D.?(3028,1011)
9.在平面直角坐标系中,点 关于 轴对称的点的坐标为(??? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
10.如图,在平面直角坐标系中,菱形ABCD的顶点A在y轴上,已知B(﹣3,0)、C(2,0),则点D的坐标为(?? )
A.?(4,5)???????????????????????????B.?(5,4)?????????????????????????
?
?C.?(5,3)???????????????????????????D.?(4,3)
11.已知点A(2x﹣4,x+2)在坐标轴上,则x的值等于(?? )
A.?2或﹣2???????????????????B.?﹣2??????????????????????????????????C.?2??????????????????????????????????D.?非上述答案
12.如图,已知三角形ABC如图所示放置在平面直角坐标系中,其中C(-4,4).则三角形ABC 的面积是(?? )
? A.?4??????????????????????????????????????????B.?6????????????????????????????????????????
?C.?12????????????????????????????????????????D.?24
二、填空题(共6题;共24分)
13.以水平数轴的原点 为圆心过正半轴 上的每一刻度点画同心圆,将 逆时针依次旋转 、 、 、 、 得到 条射线,构成如图所示的“圆”坐标系,点 、 的坐标分别表示为 、 ,则点 的坐标表示为________.
14.已知点P(﹣2,1),则点P关于x轴对称的点的坐标是________.
15.平面直角坐标系中,将点A(﹣1,2)先向左平移2个单位,再向上平移1个单位后得到的点A1的坐标为________.
16.如图,将5个大小相同的正方形置于平面直角坐标系中,若顶点M、N的坐标分别为 、 ,则顶点 的坐标为________.
17.如图:以?ABCD对角线的交点O为原点,平行于BC边的直线为x轴,建立如图所示的平面直角坐标系.若A点坐标为(﹣2,1),则C点坐标为________.
18.如图,矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则D点的坐标为________?.
三、解答题(共7题;共60分)
19.(8分)已知点A 和点B 关于 轴对称,求 的值.
20. (8分)如图,在平面直角坐标系中, , , ,求: 三个顶点的坐标.
21. (8分)已知:点A、B在平面直角坐标系中的位置如图所示,求△AOB的面积.
22. (8分)如果B(m+1,3m﹣5)到x轴的距离与它到y轴的距离相等,求:
(1)m的值;
(2)求它关于原点的对称点坐标.
23.如图,已知四边形ABCD,则四边形ABCD的面积是多少?
24. (8分)如图,已知 ,点 分别在 轴正半轴和 轴正半轴上, ,试求 的值.
25. (12分)如图,用(-1,0)表示A点的位置,用(2,1)表示B点的位置,那么:
(1)画出直角坐标系。
(2)写出△DEF的三个顶点的坐标。
(3)在图中表示出点M(6,2),N(4,4)的位置。
答案解析部分
一、单选题
1.【答案】 D
2.【答案】 D
3.【答案】 A
4.【答案】 A
5.【答案】 B
6.【答案】 C
7.【答案】 B
8.【答案】 D
9.【答案】 D
10.【答案】 B
11.【答案】 A
12.【答案】 C
二、填空题
13.【答案】 (3,240°)
14.【答案】(﹣2,﹣1)
15.【答案】 (﹣3,3)
16.【答案】 (15,3)
17.【答案】 (2,﹣1)
18.【答案】 (0,2.1)
三、解答题
19.【答案】解:∵点A ,点B 关于 轴对称,
∴ ,解得
∴
20.【答案】 根据题意有:
解答:
???
、 、
21.【答案】 设AB交x轴于C,那么根据图中的信息可知: OC=1, S△OAC= ×1×2=1, S△OBC= ×1×2=1, 因此S△OAB=S△OAC+S△OBC=2.
22.【答案】 (1)解:由题意得:m+1=3m﹣5,或m+1+3m﹣5=0,
解得:m=3或m=1
(2)解:当m=3时,B(4,4)关于原点的对称点坐标(﹣4,﹣4);
当m=1时,B(2,﹣2)关于原点的对称点坐标(﹣2,2)
23.【答案】 解:过点B作BE⊥x轴于点E,如下图所示:
四边形ABCD分成△AOD,梯形BEOA,△BCE,
S△AOD= ×OD×OA= ×1×4=2,
S梯形BEOA= ×(BE+OA)×OE= ×(3+4)×3= ,
S△BCE= ×CE×BE= ×2×3=3,
S四边形ABCD=2+ +3=15.5,
即四边形ABCD的面积为15.5.
24.【答案】 解:过 作 轴于 轴于,
,
,
轴 轴,
,
,
则四边形 是正方形,
,
,
,
,
在 和 中
,
,
,
故答案为: .
25.【答案】 (1)解:以O点为原点,水平向右为正方向画x轴,垂直往上为正方向画y轴,依此建立直角坐标系即可
(2)解:根据(1)建立的直角坐标系,D(1,2),E(4,3),F(0,4)
(3)解:在(1)建立的直角坐标系标记出点M(6,2)、N(4,4)的位置.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
