22.1.2 二次函数的图象和性质同步练习(含解析)
文档属性
| 名称 | 22.1.2 二次函数的图象和性质同步练习(含解析) |

|
|
| 格式 | rar | ||
| 文件大小 | 447.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
22.1
二次函数的图象和性质(2)
一.选择题(共9小题)
1.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax+b的图象大致是( )
A.
B.
C.
D.
2.抛物线y=ax2+bx+c与直线y=ax+c(a≠0)在同一直角坐标系中的图象可能是( )
A.
B.
C.
D.
3.在同一坐标系中一次函数y=ax+b和二次函数y=ax2+bx的图象可能为( )
A.
B.
C.
D.
4.抛物线y=5(x﹣2)2﹣3的顶点坐标是( )
A.(2,﹣3)
B.(2,3)
C.(﹣2,3)
D.(﹣2,﹣3)
5.二次函数y=ax2+bx+c的图象如图所示,则下列命题中:①b=﹣2a;②此抛物线向下移动c个单位后过点(2,0);③﹣1<a<﹣;④方程x2﹣2x+=0有实数根,结论正确的个数( )
A.1个
B.2个
C.3个
D.4个
6.抛物线y=(x﹣3)2﹣5的顶点坐标是( )
A.(3,5)
B.(﹣3,5)
C.(3,﹣5)
D.(﹣3,﹣5)
7.将二次函数y=x2+4x﹣1用配方法化成y=(x﹣h)2+k的形式,下列所配方的结果中正确的是( )
A.y=(x﹣2)2+5
B.y=(x+2)2﹣5
C.y=(x﹣4)2﹣1
D.y=(x+4)2﹣5
8.二次函数y=x2+3x+化为y=(x﹣h)2+k的形式,结果正确的是( )
A.
B.
C.
D.
9.把二次函数y=x2﹣2x化为y=a(x+b)2+c的形式,正确的是( )
A.y=(x+3)2﹣3
B.y=(x﹣3)2﹣3
C.y=(x+3)2﹣9
D.y=(x+3)2﹣9
二.填空题(共6小题)
10.二次函数y=﹣x2﹣2x图象x轴上方的部分沿x轴翻折到x轴下方,图象的其余部分保持不变,翻折后的图象与原图象x轴下方的部分组成一个“M”形状的新图象,若直线y=x+b与该新图象有两个公共点,则b的取值范围为
.
11.如图所示,在同一坐标系中,作出①y=a1x2,②y=a2x2,③y=a3x2的图象,比较a1、a2、a3大小是
.
12.二次函数y=x2+2x﹣4的图象的对称轴是
,顶点坐标是
.
13.当x=0时,函数y=2x2+1的值为
.
14.把y=﹣2x2+8x﹣8配方成y=a(x﹣h)2+k的形式为y=
.
15.二次函数y=x2+6x﹣3配方后为y=(x+3)2+
.
三.解答题(共3小题)
16.画出二次函数y=(x﹣1)2的图象.
17.抛物线y=x2+4x+3
(1)求出该抛物线对称轴和顶点坐标.
(2)在所给的平面直角坐标系中用描点法画出这条抛物线.
18.已知二次函数y=x2﹣4x+3.
(1)用配方法将其化为y=a(x﹣h)2+k的形式;
(2)在所给的平面直角坐标系xOy中,画出它的图象.
22.1
二次函数的图象和性质(2)
参考答案与试题解析
一.选择题(共9小题)
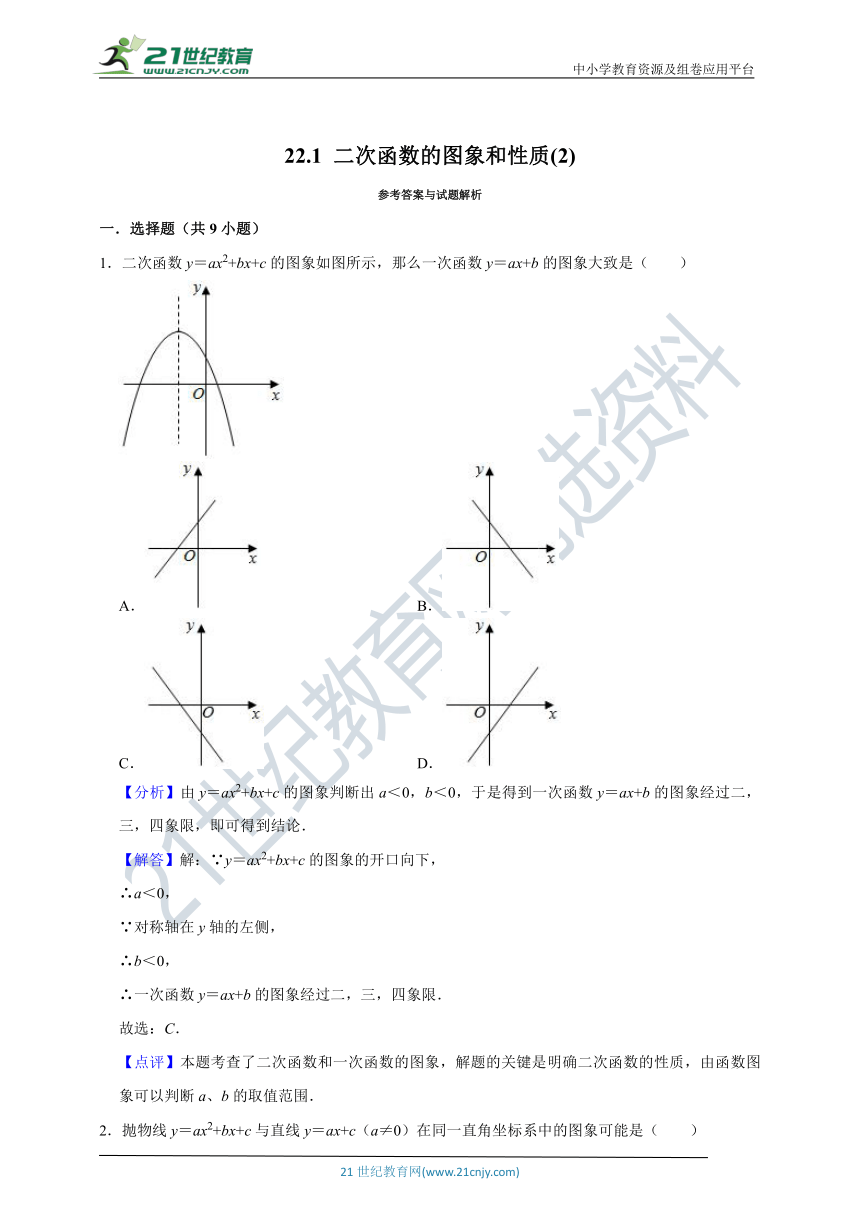
1.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax+b的图象大致是( )
A.
B.
C.
D.
【分析】由y=ax2+bx+c的图象判断出a<0,b<0,于是得到一次函数y=ax+b的图象经过二,三,四象限,即可得到结论.
【解答】解:∵y=ax2+bx+c的图象的开口向下,
∴a<0,
∵对称轴在y轴的左侧,
∴b<0,
∴一次函数y=ax+b的图象经过二,三,四象限.
故选:C.
【点评】本题考查了二次函数和一次函数的图象,解题的关键是明确二次函数的性质,由函数图象可以判断a、b的取值范围.
2.抛物线y=ax2+bx+c与直线y=ax+c(a≠0)在同一直角坐标系中的图象可能是( )
A.
B.
C.
D.
【分析】可先由一次函数y=ax+c图象得到字母系数的正负,再与二次函数y=ax2+bx+c的图象相比较看是否一致.
【解答】解:A、一次函数y=ax+c与y轴交点应为(0,c),二次函数y=ax2+bx+c与y轴交点也应为(0,c),图象不符合,故本选项错误;
B、由抛物线可知,a>0,由直线可知,a<0,a的取值矛盾,故本选项错误;
C、由抛物线可知,a<0,由直线可知,a>0,a的取值矛盾,故本选项错误;
D、由抛物线可知,a<0,由直线可知,a<0,且抛物线与直线与y轴的交点相同,故本选项正确.
故选:D.
【点评】本题考查抛物线和直线的性质,用假设法来搞定这种数形结合题是一种很好的方法.
3.在同一坐标系中一次函数y=ax+b和二次函数y=ax2+bx的图象可能为( )
A.
B.
C.
D.
【分析】可先由一次函数y=ax+b图象得到字母系数的正负,再与二次函数y=ax2+bx的图象相比较看是否一致.
【解答】解:A、由抛物线可知,a>0,x=﹣>0,得b<0,由直线可知,a>0,b<0,正确;
B、由抛物线可知,a>0,由直线可知,a<0,错误;
C、由抛物线可知,a<0,x=﹣>0,得b>0,由直线可知,a<0,b<0,错误;
D、由抛物线可知,a<0,由直线可知,a>0,错误.
故选:A.
【点评】本题主要考查了二次函数的性质和一次函数的性质,做题时要注意数形结合思想的运用,同学们加强训练即可掌握,属于基础题.
4.抛物线y=5(x﹣2)2﹣3的顶点坐标是( )
A.(2,﹣3)
B.(2,3)
C.(﹣2,3)
D.(﹣2,﹣3)
【分析】由于抛物线y=a(x﹣h)2+k的顶点坐标为(h,k),由此即可求解.
【解答】解:∵抛物线y=5(x﹣2)2﹣3,
∴顶点坐标为:(2,﹣3).
故选:A.
【点评】此题主要考查了二次函数的性质,解题的关键是熟练掌握抛物线的顶点坐标公式即可解决问题.
5.二次函数y=ax2+bx+c的图象如图所示,则下列命题中:①b=﹣2a;②此抛物线向下移动c个单位后过点(2,0);③﹣1<a<﹣;④方程x2﹣2x+=0有实数根,结论正确的个数( )
A.1个
B.2个
C.3个
D.4个
【分析】A.函数的对称轴为x=﹣=1,即可求解;
B.新抛物线表达式为:y=ax2+bx=ax2﹣2ax=ax(x﹣2),即可求解;
C.x=﹣1时,y=a﹣b+c<0,x=1时,y=a+b+c=2,即,即可求解;
D.△=4a2﹣4a=4a(a﹣1),而﹣1<a<﹣,故△>0,即可求解.
【解答】解:A.函数的对称轴为x=﹣=1,解得:b=﹣2a;
故A正确;
B.此抛物线向下移动c个单位后,新抛物线表达式为:y=ax2+bx=ax2﹣2ax=ax(x﹣2),
则x=2时,y=0,故抛物线过点(2,0),
故B正确;
C.x=﹣1时,y=a﹣b+c<0,x=1时,y=a+b+c=2,即,解得:﹣1<a<﹣,
故C正确;
D.∵c<0,
∴x2﹣2x+=0变形为cx2﹣2cx+1=0,
∵△=4c2﹣4c=4c(c﹣1),而1<c<2,
∴△>0,故方程x2﹣2x+=0有实数根,
故D正确;
故选:D.
【点评】考查二次函数y=ax2+bx+c系数符号的确定由抛物线开口方向、对称轴、与y轴的交点有关,熟练掌握二次函数的性质是解题的关键.
6.抛物线y=(x﹣3)2﹣5的顶点坐标是( )
A.(3,5)
B.(﹣3,5)
C.(3,﹣5)
D.(﹣3,﹣5)
【分析】根据抛物线y=a(x﹣h)2+k的顶点坐标是(h,k)直接写出即可.
【解答】解:抛物线y=(x﹣3)2﹣5的顶点坐标是(3,﹣5),
故选:C.
【点评】此题主要考查了二次函数的性质,关键是熟记:抛物线y=a(x﹣h)2+k的顶点坐标是(h,k),对称轴是x=h.
7.将二次函数y=x2+4x﹣1用配方法化成y=(x﹣h)2+k的形式,下列所配方的结果中正确的是( )
A.y=(x﹣2)2+5
B.y=(x+2)2﹣5
C.y=(x﹣4)2﹣1
D.y=(x+4)2﹣5
【分析】运用配方法把一般式化为顶点式即可.
【解答】解:y=x2+4x﹣1=y=x2+4x+4﹣4﹣1=(x+2)2﹣5,
故选:B.
【点评】本题考查的是二次函数的三种形式,正确运用配方法把一般式化为顶点式是解题的关键.
8.二次函数y=x2+3x+化为y=(x﹣h)2+k的形式,结果正确的是( )
A.
B.
C.
D.
【分析】利用配方法先提出二次项系数,在加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
【解答】解:y=x2+3x+=(x2+6x+9﹣9+5)=(x+3)2+2.
故选:A.
【点评】本题考查了二次函数的三种形式:一般式y=ax2+bx+c(a、b、c为常数,a≠0);顶点式y=a(x﹣k)2+h,顶点坐标为(k,h);交点式y=(x﹣x1)(x﹣x2),x1、x2为抛物线与x轴交点的横坐标.
9.把二次函数y=x2﹣2x化为y=a(x+b)2+c的形式,正确的是( )
A.y=(x+3)2﹣3
B.y=(x﹣3)2﹣3
C.y=(x+3)2﹣9
D.y=(x+3)2﹣9
【分析】直接利用配方法将原式变形得出答案.
【解答】解:y=x2﹣2x
=(x2﹣6x)
=[(x﹣3)2﹣9]
=(x﹣3)2﹣3.
故选:B.
【点评】此题主要考查了二次函数的三种形式,正确将原式变形是解题关键.
二.填空题(共6小题)
10.二次函数y=﹣x2﹣2x图象x轴上方的部分沿x轴翻折到x轴下方,图象的其余部分保持不变,翻折后的图象与原图象x轴下方的部分组成一个“M”形状的新图象,若直线y=x+b与该新图象有两个公共点,则b的取值范围为 0<b<1或b<﹣ .
【分析】画出图象求出直线经过点A和原点时的b的值,结合图象可以确定b的范围,再求出直线与翻折后的抛物线只有一个交点时的b的值,可以利用方程组只有一组解△=0解决问题,由此再确定b的取值范围.
【解答】解:如图,当直线y=x+b经过点A(﹣2,0)时,b=1,
当直线y=x+b经过点O(0,0)时,b=0,
∴0<b<1时,直线y=x+b与新图形有两个交点.
翻折后的抛物线为y=x2+2x,
由方程组有一组解,消去y得到:2x2+3x﹣2b=0,
∵△=0,
∴9+16b=0,
b=﹣,
由图象可知,b<﹣时,直线y=x+b与新图形有两个交点.
综上所述0<b<1或b<﹣时,直线y=x+b与新图形有两个交点.
【点评】本题考查一次函数、根的判别式等知识,解题的关键是正确画出图象,找关键点解决问题,把只有一个交点问题转化为方程组只有一组解解决,是数形结合的好题目,属于中考常考题型.
11.如图所示,在同一坐标系中,作出①y=a1x2,②y=a2x2,③y=a3x2的图象,比较a1、a2、a3大小是 a1>a2>a3 .
【分析】根据二次函数中二次项系数的绝对值越大抛物线开口越小进行比较即可.
【解答】解:
∵三个二次函数的图象开口都向上,
∴a1、a2、a3都为正数,
∵在y=ax2中,a的绝对值越大,抛物线开口越小,
∴a1>a2>a3,
故答案为:a1>a2>a3.
【点评】本题主要考查二次函数的图象,掌握二次函数的开口大小由二次项系数决定是解题的关键.
12.二次函数y=x2+2x﹣4的图象的对称轴是 直线x=﹣1 ,顶点坐标是 (﹣1,﹣5) .
【分析】先将题目中的函数解析式化为顶点式,即可得到该函数图象的对称轴和顶点坐标.
【解答】解:∵y=x2+2x﹣4=(x+1)2﹣5,
∴该函数图象的对称轴是直线x=﹣1,顶点坐标为(﹣1,﹣5),
故答案为:直线x=﹣1,(﹣1,﹣5).
【点评】本题考查二次函数的性质、二次函数图象,解答本题的关键是明确题意,利用二次函数的性质解答.
13.当x=0时,函数y=2x2+1的值为 1 .
【分析】直接把x的值代入进而求出答案.
【解答】解:当x=0时,函数y=2x2+1=0+1=1.
故答案为:1.
【点评】此题主要考查了二次函数的性质,正确代入x的值是解题关键.
14.把y=﹣2x2+8x﹣8配方成y=a(x﹣h)2+k的形式为y= ﹣2(x﹣2)2 .
【分析】直接利用配方法将原式变形进而得出答案.
【解答】解:y=﹣2x2+8x﹣8
=﹣2(x2﹣4x+4)
=﹣2(x﹣2)2.
故答案为:﹣2(x﹣2)2.
【点评】此题主要考查了二次函数的三种形式,正确进行配方是解题关键.
15.二次函数y=x2+6x﹣3配方后为y=(x+3)2+ (﹣12) .
【分析】由于二次项系数为1,所以右边加上一次项系数一半的平方,再减去一次项系数一半的平方,化简,即可得出结论.
【解答】解:∵y=x2+6x﹣3
=(x2+6x)﹣3
=(x2+6x+32﹣32)﹣3
=(x+3)2﹣9﹣3
=(x+3)2﹣12,
故答案为:(﹣12).
【点评】此题主要考查了二次函数的三种形式的互化,掌握配方法是解本题的关键.
三.解答题(共3小题)
16.画出二次函数y=(x﹣1)2的图象.
【分析】首先可得顶点坐标为(1,0),然后利用对称性列表,再描点,连线,即可作出该函数的图象.
【解答】解:列表得:
x
…
﹣1
0
1
2
3
…
y
…
4
1
0
1
4
…
如图:
.
【点评】此题考查了二次函数的图象.注意确定此二次函数的顶点坐标是关键.
17.抛物线y=x2+4x+3
(1)求出该抛物线对称轴和顶点坐标.
(2)在所给的平面直角坐标系中用描点法画出这条抛物线.
【分析】(1)首先利用配方法把解析式写成顶点式,再确定顶点坐标和对称轴即可;
(2)计算出y=0时,x2+4x+3=0的x值,进而可得抛物线与x轴交于点(﹣1,0)(﹣3,0),再描点画抛物线即可.
【解答】解:(1)y=x2+4x+3=x2+4x+4﹣4+3=(x+2)2﹣1,
顶点坐标为(﹣2,﹣1),
对称轴为x=﹣2;
(2)当y=0时,x2+4x+3=0,
则(x+1)(x+3)=0,
解得:x1=﹣1,x2=﹣3,
∴抛物线与x轴交于点(﹣1,0)(﹣3,0),
图象如图所示.
【点评】此题主要考查了二次函数的性质,关键是掌握二次函数顶点式.
18.已知二次函数y=x2﹣4x+3.
(1)用配方法将其化为y=a(x﹣h)2+k的形式;
(2)在所给的平面直角坐标系xOy中,画出它的图象.
【分析】(1)利用配方法把二次函数解析式化成顶点式即可;
(2)利用描点法画出二次函数图象即可.
【解答】解:(1)y=x2﹣4x+3
=x2﹣4x+22﹣22+3=(x﹣2)2﹣1;
(2))∵y=(x﹣2)2﹣1,
∴顶点坐标为(2,﹣1),对称轴方程为x=2.
∵函数二次函数y=x2﹣4x+3的开口向上,顶点坐标为(2,﹣1),与x轴的交点为(3,0),(1,0),
∴其图象为:
【点评】本题考查了二次函数的配方法,用描点法画二次函数的图象,掌握配方法是解答此题的关键.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/8
9:52:31;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
22.1
二次函数的图象和性质(2)
一.选择题(共9小题)
1.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax+b的图象大致是( )
A.
B.
C.
D.
2.抛物线y=ax2+bx+c与直线y=ax+c(a≠0)在同一直角坐标系中的图象可能是( )
A.
B.
C.
D.
3.在同一坐标系中一次函数y=ax+b和二次函数y=ax2+bx的图象可能为( )
A.
B.
C.
D.
4.抛物线y=5(x﹣2)2﹣3的顶点坐标是( )
A.(2,﹣3)
B.(2,3)
C.(﹣2,3)
D.(﹣2,﹣3)
5.二次函数y=ax2+bx+c的图象如图所示,则下列命题中:①b=﹣2a;②此抛物线向下移动c个单位后过点(2,0);③﹣1<a<﹣;④方程x2﹣2x+=0有实数根,结论正确的个数( )
A.1个
B.2个
C.3个
D.4个
6.抛物线y=(x﹣3)2﹣5的顶点坐标是( )
A.(3,5)
B.(﹣3,5)
C.(3,﹣5)
D.(﹣3,﹣5)
7.将二次函数y=x2+4x﹣1用配方法化成y=(x﹣h)2+k的形式,下列所配方的结果中正确的是( )
A.y=(x﹣2)2+5
B.y=(x+2)2﹣5
C.y=(x﹣4)2﹣1
D.y=(x+4)2﹣5
8.二次函数y=x2+3x+化为y=(x﹣h)2+k的形式,结果正确的是( )
A.
B.
C.
D.
9.把二次函数y=x2﹣2x化为y=a(x+b)2+c的形式,正确的是( )
A.y=(x+3)2﹣3
B.y=(x﹣3)2﹣3
C.y=(x+3)2﹣9
D.y=(x+3)2﹣9
二.填空题(共6小题)
10.二次函数y=﹣x2﹣2x图象x轴上方的部分沿x轴翻折到x轴下方,图象的其余部分保持不变,翻折后的图象与原图象x轴下方的部分组成一个“M”形状的新图象,若直线y=x+b与该新图象有两个公共点,则b的取值范围为
.
11.如图所示,在同一坐标系中,作出①y=a1x2,②y=a2x2,③y=a3x2的图象,比较a1、a2、a3大小是
.
12.二次函数y=x2+2x﹣4的图象的对称轴是
,顶点坐标是
.
13.当x=0时,函数y=2x2+1的值为
.
14.把y=﹣2x2+8x﹣8配方成y=a(x﹣h)2+k的形式为y=
.
15.二次函数y=x2+6x﹣3配方后为y=(x+3)2+
.
三.解答题(共3小题)
16.画出二次函数y=(x﹣1)2的图象.
17.抛物线y=x2+4x+3
(1)求出该抛物线对称轴和顶点坐标.
(2)在所给的平面直角坐标系中用描点法画出这条抛物线.
18.已知二次函数y=x2﹣4x+3.
(1)用配方法将其化为y=a(x﹣h)2+k的形式;
(2)在所给的平面直角坐标系xOy中,画出它的图象.
22.1
二次函数的图象和性质(2)
参考答案与试题解析
一.选择题(共9小题)
1.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax+b的图象大致是( )
A.
B.
C.
D.
【分析】由y=ax2+bx+c的图象判断出a<0,b<0,于是得到一次函数y=ax+b的图象经过二,三,四象限,即可得到结论.
【解答】解:∵y=ax2+bx+c的图象的开口向下,
∴a<0,
∵对称轴在y轴的左侧,
∴b<0,
∴一次函数y=ax+b的图象经过二,三,四象限.
故选:C.
【点评】本题考查了二次函数和一次函数的图象,解题的关键是明确二次函数的性质,由函数图象可以判断a、b的取值范围.
2.抛物线y=ax2+bx+c与直线y=ax+c(a≠0)在同一直角坐标系中的图象可能是( )
A.
B.
C.
D.
【分析】可先由一次函数y=ax+c图象得到字母系数的正负,再与二次函数y=ax2+bx+c的图象相比较看是否一致.
【解答】解:A、一次函数y=ax+c与y轴交点应为(0,c),二次函数y=ax2+bx+c与y轴交点也应为(0,c),图象不符合,故本选项错误;
B、由抛物线可知,a>0,由直线可知,a<0,a的取值矛盾,故本选项错误;
C、由抛物线可知,a<0,由直线可知,a>0,a的取值矛盾,故本选项错误;
D、由抛物线可知,a<0,由直线可知,a<0,且抛物线与直线与y轴的交点相同,故本选项正确.
故选:D.
【点评】本题考查抛物线和直线的性质,用假设法来搞定这种数形结合题是一种很好的方法.
3.在同一坐标系中一次函数y=ax+b和二次函数y=ax2+bx的图象可能为( )
A.
B.
C.
D.
【分析】可先由一次函数y=ax+b图象得到字母系数的正负,再与二次函数y=ax2+bx的图象相比较看是否一致.
【解答】解:A、由抛物线可知,a>0,x=﹣>0,得b<0,由直线可知,a>0,b<0,正确;
B、由抛物线可知,a>0,由直线可知,a<0,错误;
C、由抛物线可知,a<0,x=﹣>0,得b>0,由直线可知,a<0,b<0,错误;
D、由抛物线可知,a<0,由直线可知,a>0,错误.
故选:A.
【点评】本题主要考查了二次函数的性质和一次函数的性质,做题时要注意数形结合思想的运用,同学们加强训练即可掌握,属于基础题.
4.抛物线y=5(x﹣2)2﹣3的顶点坐标是( )
A.(2,﹣3)
B.(2,3)
C.(﹣2,3)
D.(﹣2,﹣3)
【分析】由于抛物线y=a(x﹣h)2+k的顶点坐标为(h,k),由此即可求解.
【解答】解:∵抛物线y=5(x﹣2)2﹣3,
∴顶点坐标为:(2,﹣3).
故选:A.
【点评】此题主要考查了二次函数的性质,解题的关键是熟练掌握抛物线的顶点坐标公式即可解决问题.
5.二次函数y=ax2+bx+c的图象如图所示,则下列命题中:①b=﹣2a;②此抛物线向下移动c个单位后过点(2,0);③﹣1<a<﹣;④方程x2﹣2x+=0有实数根,结论正确的个数( )
A.1个
B.2个
C.3个
D.4个
【分析】A.函数的对称轴为x=﹣=1,即可求解;
B.新抛物线表达式为:y=ax2+bx=ax2﹣2ax=ax(x﹣2),即可求解;
C.x=﹣1时,y=a﹣b+c<0,x=1时,y=a+b+c=2,即,即可求解;
D.△=4a2﹣4a=4a(a﹣1),而﹣1<a<﹣,故△>0,即可求解.
【解答】解:A.函数的对称轴为x=﹣=1,解得:b=﹣2a;
故A正确;
B.此抛物线向下移动c个单位后,新抛物线表达式为:y=ax2+bx=ax2﹣2ax=ax(x﹣2),
则x=2时,y=0,故抛物线过点(2,0),
故B正确;
C.x=﹣1时,y=a﹣b+c<0,x=1时,y=a+b+c=2,即,解得:﹣1<a<﹣,
故C正确;
D.∵c<0,
∴x2﹣2x+=0变形为cx2﹣2cx+1=0,
∵△=4c2﹣4c=4c(c﹣1),而1<c<2,
∴△>0,故方程x2﹣2x+=0有实数根,
故D正确;
故选:D.
【点评】考查二次函数y=ax2+bx+c系数符号的确定由抛物线开口方向、对称轴、与y轴的交点有关,熟练掌握二次函数的性质是解题的关键.
6.抛物线y=(x﹣3)2﹣5的顶点坐标是( )
A.(3,5)
B.(﹣3,5)
C.(3,﹣5)
D.(﹣3,﹣5)
【分析】根据抛物线y=a(x﹣h)2+k的顶点坐标是(h,k)直接写出即可.
【解答】解:抛物线y=(x﹣3)2﹣5的顶点坐标是(3,﹣5),
故选:C.
【点评】此题主要考查了二次函数的性质,关键是熟记:抛物线y=a(x﹣h)2+k的顶点坐标是(h,k),对称轴是x=h.
7.将二次函数y=x2+4x﹣1用配方法化成y=(x﹣h)2+k的形式,下列所配方的结果中正确的是( )
A.y=(x﹣2)2+5
B.y=(x+2)2﹣5
C.y=(x﹣4)2﹣1
D.y=(x+4)2﹣5
【分析】运用配方法把一般式化为顶点式即可.
【解答】解:y=x2+4x﹣1=y=x2+4x+4﹣4﹣1=(x+2)2﹣5,
故选:B.
【点评】本题考查的是二次函数的三种形式,正确运用配方法把一般式化为顶点式是解题的关键.
8.二次函数y=x2+3x+化为y=(x﹣h)2+k的形式,结果正确的是( )
A.
B.
C.
D.
【分析】利用配方法先提出二次项系数,在加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
【解答】解:y=x2+3x+=(x2+6x+9﹣9+5)=(x+3)2+2.
故选:A.
【点评】本题考查了二次函数的三种形式:一般式y=ax2+bx+c(a、b、c为常数,a≠0);顶点式y=a(x﹣k)2+h,顶点坐标为(k,h);交点式y=(x﹣x1)(x﹣x2),x1、x2为抛物线与x轴交点的横坐标.
9.把二次函数y=x2﹣2x化为y=a(x+b)2+c的形式,正确的是( )
A.y=(x+3)2﹣3
B.y=(x﹣3)2﹣3
C.y=(x+3)2﹣9
D.y=(x+3)2﹣9
【分析】直接利用配方法将原式变形得出答案.
【解答】解:y=x2﹣2x
=(x2﹣6x)
=[(x﹣3)2﹣9]
=(x﹣3)2﹣3.
故选:B.
【点评】此题主要考查了二次函数的三种形式,正确将原式变形是解题关键.
二.填空题(共6小题)
10.二次函数y=﹣x2﹣2x图象x轴上方的部分沿x轴翻折到x轴下方,图象的其余部分保持不变,翻折后的图象与原图象x轴下方的部分组成一个“M”形状的新图象,若直线y=x+b与该新图象有两个公共点,则b的取值范围为 0<b<1或b<﹣ .
【分析】画出图象求出直线经过点A和原点时的b的值,结合图象可以确定b的范围,再求出直线与翻折后的抛物线只有一个交点时的b的值,可以利用方程组只有一组解△=0解决问题,由此再确定b的取值范围.
【解答】解:如图,当直线y=x+b经过点A(﹣2,0)时,b=1,
当直线y=x+b经过点O(0,0)时,b=0,
∴0<b<1时,直线y=x+b与新图形有两个交点.
翻折后的抛物线为y=x2+2x,
由方程组有一组解,消去y得到:2x2+3x﹣2b=0,
∵△=0,
∴9+16b=0,
b=﹣,
由图象可知,b<﹣时,直线y=x+b与新图形有两个交点.
综上所述0<b<1或b<﹣时,直线y=x+b与新图形有两个交点.
【点评】本题考查一次函数、根的判别式等知识,解题的关键是正确画出图象,找关键点解决问题,把只有一个交点问题转化为方程组只有一组解解决,是数形结合的好题目,属于中考常考题型.
11.如图所示,在同一坐标系中,作出①y=a1x2,②y=a2x2,③y=a3x2的图象,比较a1、a2、a3大小是 a1>a2>a3 .
【分析】根据二次函数中二次项系数的绝对值越大抛物线开口越小进行比较即可.
【解答】解:
∵三个二次函数的图象开口都向上,
∴a1、a2、a3都为正数,
∵在y=ax2中,a的绝对值越大,抛物线开口越小,
∴a1>a2>a3,
故答案为:a1>a2>a3.
【点评】本题主要考查二次函数的图象,掌握二次函数的开口大小由二次项系数决定是解题的关键.
12.二次函数y=x2+2x﹣4的图象的对称轴是 直线x=﹣1 ,顶点坐标是 (﹣1,﹣5) .
【分析】先将题目中的函数解析式化为顶点式,即可得到该函数图象的对称轴和顶点坐标.
【解答】解:∵y=x2+2x﹣4=(x+1)2﹣5,
∴该函数图象的对称轴是直线x=﹣1,顶点坐标为(﹣1,﹣5),
故答案为:直线x=﹣1,(﹣1,﹣5).
【点评】本题考查二次函数的性质、二次函数图象,解答本题的关键是明确题意,利用二次函数的性质解答.
13.当x=0时,函数y=2x2+1的值为 1 .
【分析】直接把x的值代入进而求出答案.
【解答】解:当x=0时,函数y=2x2+1=0+1=1.
故答案为:1.
【点评】此题主要考查了二次函数的性质,正确代入x的值是解题关键.
14.把y=﹣2x2+8x﹣8配方成y=a(x﹣h)2+k的形式为y= ﹣2(x﹣2)2 .
【分析】直接利用配方法将原式变形进而得出答案.
【解答】解:y=﹣2x2+8x﹣8
=﹣2(x2﹣4x+4)
=﹣2(x﹣2)2.
故答案为:﹣2(x﹣2)2.
【点评】此题主要考查了二次函数的三种形式,正确进行配方是解题关键.
15.二次函数y=x2+6x﹣3配方后为y=(x+3)2+ (﹣12) .
【分析】由于二次项系数为1,所以右边加上一次项系数一半的平方,再减去一次项系数一半的平方,化简,即可得出结论.
【解答】解:∵y=x2+6x﹣3
=(x2+6x)﹣3
=(x2+6x+32﹣32)﹣3
=(x+3)2﹣9﹣3
=(x+3)2﹣12,
故答案为:(﹣12).
【点评】此题主要考查了二次函数的三种形式的互化,掌握配方法是解本题的关键.
三.解答题(共3小题)
16.画出二次函数y=(x﹣1)2的图象.
【分析】首先可得顶点坐标为(1,0),然后利用对称性列表,再描点,连线,即可作出该函数的图象.
【解答】解:列表得:
x
…
﹣1
0
1
2
3
…
y
…
4
1
0
1
4
…
如图:
.
【点评】此题考查了二次函数的图象.注意确定此二次函数的顶点坐标是关键.
17.抛物线y=x2+4x+3
(1)求出该抛物线对称轴和顶点坐标.
(2)在所给的平面直角坐标系中用描点法画出这条抛物线.
【分析】(1)首先利用配方法把解析式写成顶点式,再确定顶点坐标和对称轴即可;
(2)计算出y=0时,x2+4x+3=0的x值,进而可得抛物线与x轴交于点(﹣1,0)(﹣3,0),再描点画抛物线即可.
【解答】解:(1)y=x2+4x+3=x2+4x+4﹣4+3=(x+2)2﹣1,
顶点坐标为(﹣2,﹣1),
对称轴为x=﹣2;
(2)当y=0时,x2+4x+3=0,
则(x+1)(x+3)=0,
解得:x1=﹣1,x2=﹣3,
∴抛物线与x轴交于点(﹣1,0)(﹣3,0),
图象如图所示.
【点评】此题主要考查了二次函数的性质,关键是掌握二次函数顶点式.
18.已知二次函数y=x2﹣4x+3.
(1)用配方法将其化为y=a(x﹣h)2+k的形式;
(2)在所给的平面直角坐标系xOy中,画出它的图象.
【分析】(1)利用配方法把二次函数解析式化成顶点式即可;
(2)利用描点法画出二次函数图象即可.
【解答】解:(1)y=x2﹣4x+3
=x2﹣4x+22﹣22+3=(x﹣2)2﹣1;
(2))∵y=(x﹣2)2﹣1,
∴顶点坐标为(2,﹣1),对称轴方程为x=2.
∵函数二次函数y=x2﹣4x+3的开口向上,顶点坐标为(2,﹣1),与x轴的交点为(3,0),(1,0),
∴其图象为:
【点评】本题考查了二次函数的配方法,用描点法画二次函数的图象,掌握配方法是解答此题的关键.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/8
9:52:31;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
同课章节目录
