22.2 二次函数与一元二次方程同步练习(含解析)
文档属性
| 名称 | 22.2 二次函数与一元二次方程同步练习(含解析) |

|
|
| 格式 | rar | ||
| 文件大小 | 305.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
22.2
二次函数与一元二次方程
一.选择题(共6小题)
1.已知二次函数y=﹣x2+2x+4,则下列关于这个函数图象和性质的说法,正确的是( )
A.图象的开口向上
B.图象的顶点坐标是(1,3)
C.当x<1时,y随x的增大而增大
D.图象与x轴有唯一交点
2.在平面直角坐标系中,已知a≠b,设函数y=(x﹣a)(x﹣b)的图象与x轴有M个交点,函数y=(ax+1)(bx+1)的图形与x轴有N个交点,则( )
A.M=N﹣1或M=N+1
B.M=N﹣1或M=N+2
C.M=N或M=N+1
D.M=N或M=N﹣1
3.已知抛物线y=x2﹣x﹣1与x轴的一个交点为(m,0),则代数式﹣2m2+2m+2020的值为( )
A.2018
B.2019
C.2020
D.2021
4.已知y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=2.若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两个根,且x1<x2,﹣1<x1<0,则下列说法正确的是( )
A.x1+x2<0
B.4<x2<5
C.b2﹣4ac<0
D.ab>0
5.二次函数y=﹣x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )
A.t>﹣5
B.﹣5<t<3
C.3<t≤4
D.﹣5<t≤4
6.表给出了二次函数y=ax2+bx+c(a≠0)的自变量x与函数值y的部分对应值:那么方程ax2+bx+c=0的一个根的近似值可能是( )
x
…
1
1.1
1.2
1.3
1.4
…
y
…
﹣1
﹣0.49
0.04
0.59
1.16
…
A.1.08
B.1.18
C.1.28
D.1.38
二.填空题(共4小题)
7.已知抛物线y=x2+bx+c的部分图象如图所示,当y<0时,x的取值范围是
.
8.若关于x的函数y=kx2+2x﹣与x轴仅有一个交点,则实数k的值为
.
9.根据下列表格中y=ax2+bx+c的自变量x与函数值y的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是
.
x
6.17
6.18
6.19
6.20
y=ax2+bx+c
﹣0.03
﹣0.01
0.02
0.04
10.在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是
.
三.解答题(共2小题)
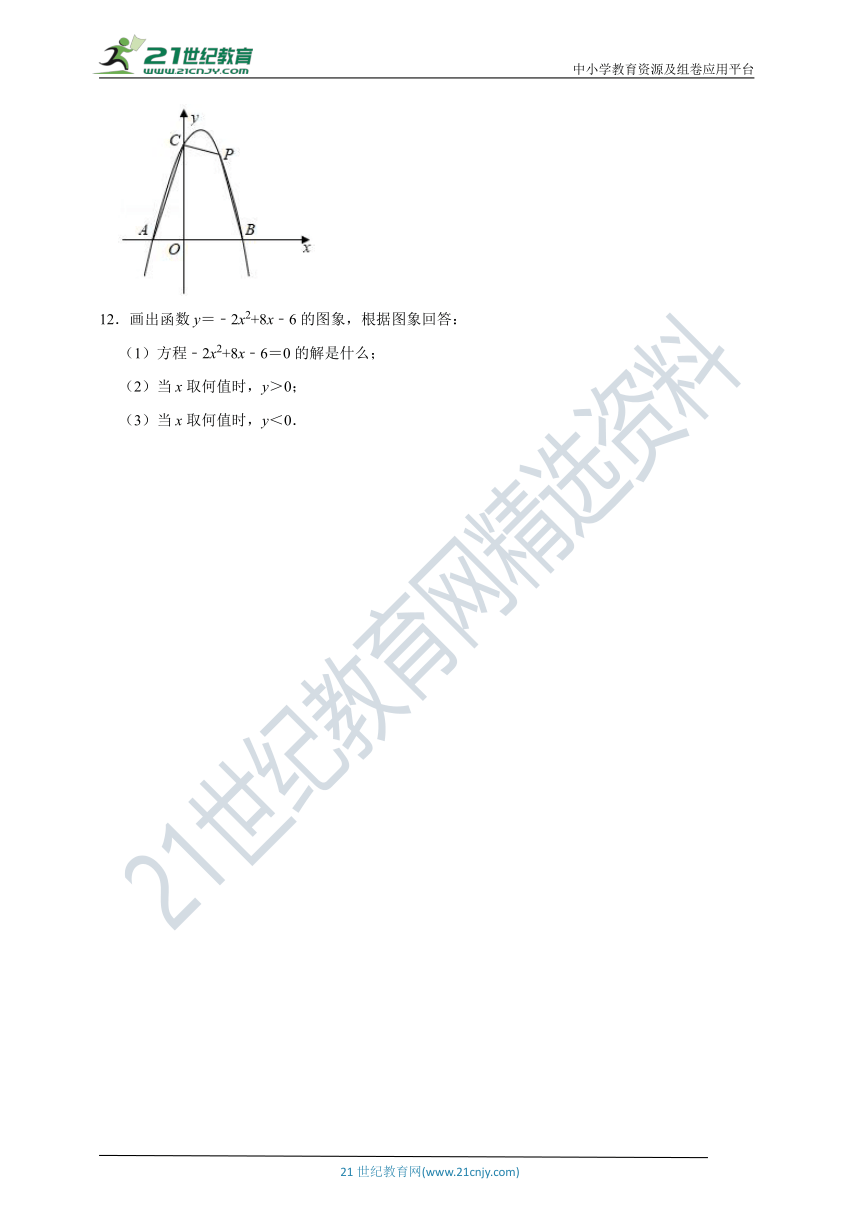
11.如图,开口向下的抛物线与x轴交于点A(﹣1,0)、B(2,0),与y轴交于点C(0,4),点P是第一象限内抛物线上的一点.
(1)求该抛物线所对应的函数解析式;
(2)设四边形CABP的面积为S,求S的最大值.
12.画出函数y=﹣2x2+8x﹣6的图象,根据图象回答:
(1)方程﹣2x2+8x﹣6=0的解是什么;
(2)当x取何值时,y>0;
(3)当x取何值时,y<0.
22.2
二次函数与一元二次方程
参考答案与试题解析
一.选择题(共6小题)
1.已知二次函数y=﹣x2+2x+4,则下列关于这个函数图象和性质的说法,正确的是( )
A.图象的开口向上
B.图象的顶点坐标是(1,3)
C.当x<1时,y随x的增大而增大
D.图象与x轴有唯一交点
【分析】先利用配方法得到y=﹣(x﹣1)2+5,可根据二次函数的性质可对A、B、C进行判断;通过解方程﹣x2+2x+4=0可对D进行判断.
【解答】解:∵y=﹣x2+2x+4=﹣(x﹣1)2+5,
∴抛物线的开口向下,顶点坐标为(1,5),抛物线的对称轴为直线x=1,当x<1时,y随x的增大而增大,
令y=0,则﹣x2+2x+4=0,解方程解得x1=1+,x2=1﹣,
∴△=4﹣4×(﹣1)×4=20>0,
∴抛物线与x轴有两个交点.
故选:C.
【点评】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程根的判断.也考查了二次函数的性质.
2.在平面直角坐标系中,已知a≠b,设函数y=(x﹣a)(x﹣b)的图象与x轴有M个交点,函数y=(ax+1)(bx+1)的图形与x轴有N个交点,则( )
A.M=N﹣1或M=N+1
B.M=N﹣1或M=N+2
C.M=N或M=N+1
D.M=N或M=N﹣1
【分析】解方程(x﹣a)(x﹣b)=0可判断抛物线y=(x﹣a)(x﹣b)与x轴有两个交点,则M=2,当y=0时,(ax+1)(bx+1)=0,讨论:当a≠0,b≠0或a=0,b≠0或b=0,a≠0可得到函数与x轴的交点个数,从而得到N的值,然后对各选项进行判断.
【解答】解:当y=0时,(x﹣a)(x﹣b)=0,解得x1=a,x2=b,抛物线y=(x﹣a)(x﹣b)与x轴的交点为(a,0),(b,0),
所以M=2,
当y=0时,(ax+1)(bx+1)=0,当a≠0,b≠0,解得x1=﹣,x2=﹣,抛物线y=(ax+1)(bx+1)与x轴的交点为(﹣,0),(﹣,0),此时N=2,
当a=0,b≠0,或b=0,a≠0时,函数y=(ax+1)(bx+1)为一次函数,则N=1,
所以M=N,M=N+1.
故选:C.
【点评】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了一次函数图象.
3.已知抛物线y=x2﹣x﹣1与x轴的一个交点为(m,0),则代数式﹣2m2+2m+2020的值为( )
A.2018
B.2019
C.2020
D.2021
【分析】将(m,0)代入抛物线表达式得:m2﹣m﹣1=0,即可求解.
【解答】解:将(m,0)代入抛物线表达式得:m2﹣m﹣1=0,
则﹣2m2+2m+2020=﹣2(m2﹣m)+2020=﹣2+2020=2018,
故选:A.
【点评】本题考查的是抛物线与x轴的交点,将点(m,0)代入函数表达式是解题的关键.
4.已知y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=2.若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两个根,且x1<x2,﹣1<x1<0,则下列说法正确的是( )
A.x1+x2<0
B.4<x2<5
C.b2﹣4ac<0
D.ab>0
【分析】利用函数图象分别得出抛物线与x轴交点的横坐标的关系,进而判断四个结论得出答案.
【解答】解:∵x1,x2是一元二次方程ax2+bx+c=0的两个根,
∴x1、x2是抛物线与x轴交点的横坐标,
∵抛物线的对称轴为x=2,
∴=2,即x1+x2=4>0,故选项A错误;
∵x1<x2,﹣1<x1<0,
∴﹣1<4﹣x2<0,
解得:4<x2<5,故选项B正确;
∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,故选项C错误;
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为x=2,
∴﹣=2,
∴b=﹣4a>0,
∴ab<0,故选项D错误;
故选:B.
【点评】主要考查二次函数与一元二次方程之间的关系,会利用对称轴的值求抛物线与x轴交点的横坐标间的数量关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.
5.二次函数y=﹣x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )
A.t>﹣5
B.﹣5<t<3
C.3<t≤4
D.﹣5<t≤4
【分析】如图,关于x的一元二次方程﹣x2+mx﹣t=0的解就是抛物线y=﹣x2+mx与直线y=t的交点的横坐标,利用图象法即可解决问题.
【解答】解:如图,关于x的一元二次方程﹣x2+mx﹣t=0的解就是抛物线y=﹣x2+mx与直线y=t的交点的横坐标,
当x=1时,y=3,
当x=5时,y=﹣5,
由图象可知关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,
直线y=t在直线y=﹣5和直线y=4之间包括直线y=4,
∴﹣5<t≤4.
故选:D.
【点评】本题考查抛物线与x轴的交点、一元二次方程等知识,解题的关键是学会利用图象法解决问题,画出图象是解决问题的关键,属于中考选择题中的压轴题.
6.表给出了二次函数y=ax2+bx+c(a≠0)的自变量x与函数值y的部分对应值:那么方程ax2+bx+c=0的一个根的近似值可能是( )
x
…
1
1.1
1.2
1.3
1.4
…
y
…
﹣1
﹣0.49
0.04
0.59
1.16
…
A.1.08
B.1.18
C.1.28
D.1.38
【分析】观察表中数据得到抛物线y=ax2+bx+c与x轴的一个交点在(1.1,0)和点(1.2,0)之间,更靠近点(1.2,0),然后根据抛物线与x轴的交点问题可得到方程ax2+bx+c=0一个根的近似值.
【解答】解:∵x=1.1时,y=ax2+bx+c=﹣0.49;x=1.2时,y=ax2+bx+c=0.04;
∴抛物线y=ax2+bx+c与x轴的一个交点在(1.1,0)和点(1.2,0)之间,更靠近点(1.2,0),
∴方程ax2+bx+c=0有一个根约为1.2.
故选:B.
【点评】本题考查了图象法求一元二次方程的近似根:通过表中数据确定抛物线与x轴的交点横坐标的范围,从而得到一元二次方程的根(由于作图或观察存在误差,由图象求得的根一般是近似的).
二.填空题(共4小题)
7.已知抛物线y=x2+bx+c的部分图象如图所示,当y<0时,x的取值范围是 ﹣1<x<3 .
【分析】根据函数图象和二次函数的性质,可以得到该抛物线与x轴的另一个交点,从而可以得到当y<0时,x的取值范围.
【解答】解:由图象可得,
该抛物线的对称轴为直线x=1,与x轴的一个交点为(﹣1,0),
故抛物线与x轴的另一个交点为(3,0),
故当y<0时,x的取值范围是﹣1<x<3.
【点评】本题考查抛物线与x轴的交点、二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质和数形结合的思想解答.
8.若关于x的函数y=kx2+2x﹣与x轴仅有一个交点,则实数k的值为 0或﹣ .
【分析】讨论:当k=0时,函数为一次函数y=2x﹣,满足条件;当k≠0时,根据判别式的意义得到△=22﹣4k×(﹣)=0,解方程得k的值.
【解答】解:当k=0时,函数为一次函数y=2x﹣,此函数与x轴只有一个交点;
当k≠0时,∵二次函数y=kx2+2x﹣与x轴仅有一个交点,
∴△=22﹣4k×(﹣)=0,解得k=﹣,
综上所述,实数k的值为0或﹣.
故答案为0或﹣.
【点评】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程;△=b2﹣4ac决定抛物线与x轴的交点个数.
9.根据下列表格中y=ax2+bx+c的自变量x与函数值y的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是 6.18<x<6.19 .
x
6.17
6.18
6.19
6.20
y=ax2+bx+c
﹣0.03
﹣0.01
0.02
0.04
【分析】利用二次函数和一元二次方程的性质.
【解答】解:由表格中的数据看出﹣0.01和0.02更接近于0,故x应取对应的范围.
故答案为:6.18<x<6.19.
【点评】本题考查了用图象法求一元二次方程的近似根,解题的关键是找到y由正变为负时,自变量的取值即可.
10.在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是 ﹣1<x2<0 .
【分析】利用对称轴及二次函数的图象性质,可以把图象与x轴另一个交点的取值范围确定.
【解答】解:由图象可知x=2时,y<0;x=3时,y>0;
由于直线x=1是它的对称轴,则由二次函数图象的对称性可知:x=0时,y<0;x=﹣1时,y>0;
所以另一个根x2的取值范围为﹣1<x2<0.
故答案为:﹣1<x2<0.
【点评】本题考查了图象法求一元二次方程的近似根,根据图象信息确定出图象与x轴交点的位置是解题的关键.
三.解答题(共2小题)
11.如图,开口向下的抛物线与x轴交于点A(﹣1,0)、B(2,0),与y轴交于点C(0,4),点P是第一象限内抛物线上的一点.
(1)求该抛物线所对应的函数解析式;
(2)设四边形CABP的面积为S,求S的最大值.
【分析】(1)设二次函数表达式为y=a(x+1)(x﹣2),再将点C代入,求出a值即可;
(2)连接OP,设点P坐标为(m,﹣2m2+2m+4),m>0,利用S四边形CABP=S△OAC+S△OCP+S△OPB得出S关于m的表达式,再求最值即可.
【解答】解:(1)∵A(﹣1,0),B(2,0),C(0,4),
设抛物线表达式为:y=a(x+1)(x﹣2),
将C代入得:4=﹣2a,
解得:a=﹣2,
∴该抛物线的解析式为:y=﹣2(x+1)(x﹣2)=﹣2x2+2x+4;
(2)连接OP,设点P坐标为(m,﹣2m2+2m+4),m>0,
∵A(﹣1,0),B(2,0),C(0,4),
可得:OA=1,OC=4,OB=2,
∴S=S四边形CABP=S△OAC+S△OCP+S△OPB
=×1×4+×4m+×2×(﹣2m2+2m+4)
=﹣2m2+4m+6
=﹣2(m﹣1)2+8,
当m=1时,S最大,最大值为8.
【点评】本题考查了二次函数的应用,待定系数法求二次函数表达式,解题的关键是能将四边形CABP的面积表示出来.
12.画出函数y=﹣2x2+8x﹣6的图象,根据图象回答:
(1)方程﹣2x2+8x﹣6=0的解是什么;
(2)当x取何值时,y>0;
(3)当x取何值时,y<0.
【分析】利用描点连线的方法画出函数y=﹣2x2+8x﹣6的图象.再根据图象判断函数的增减性.
【解答】解:函数y=﹣2x2+8x﹣6的图象如图.由图象可知:
(1)方程﹣2x2+8x﹣6=0的解x1=1,x2=3.
(2)当1<x<3时,y>0.
(3)当x<1或x>3时,y<0.
【点评】本题重点考查了函数图象的画法及解读.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/8
10:03:57;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
22.2
二次函数与一元二次方程
一.选择题(共6小题)
1.已知二次函数y=﹣x2+2x+4,则下列关于这个函数图象和性质的说法,正确的是( )
A.图象的开口向上
B.图象的顶点坐标是(1,3)
C.当x<1时,y随x的增大而增大
D.图象与x轴有唯一交点
2.在平面直角坐标系中,已知a≠b,设函数y=(x﹣a)(x﹣b)的图象与x轴有M个交点,函数y=(ax+1)(bx+1)的图形与x轴有N个交点,则( )
A.M=N﹣1或M=N+1
B.M=N﹣1或M=N+2
C.M=N或M=N+1
D.M=N或M=N﹣1
3.已知抛物线y=x2﹣x﹣1与x轴的一个交点为(m,0),则代数式﹣2m2+2m+2020的值为( )
A.2018
B.2019
C.2020
D.2021
4.已知y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=2.若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两个根,且x1<x2,﹣1<x1<0,则下列说法正确的是( )
A.x1+x2<0
B.4<x2<5
C.b2﹣4ac<0
D.ab>0
5.二次函数y=﹣x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )
A.t>﹣5
B.﹣5<t<3
C.3<t≤4
D.﹣5<t≤4
6.表给出了二次函数y=ax2+bx+c(a≠0)的自变量x与函数值y的部分对应值:那么方程ax2+bx+c=0的一个根的近似值可能是( )
x
…
1
1.1
1.2
1.3
1.4
…
y
…
﹣1
﹣0.49
0.04
0.59
1.16
…
A.1.08
B.1.18
C.1.28
D.1.38
二.填空题(共4小题)
7.已知抛物线y=x2+bx+c的部分图象如图所示,当y<0时,x的取值范围是
.
8.若关于x的函数y=kx2+2x﹣与x轴仅有一个交点,则实数k的值为
.
9.根据下列表格中y=ax2+bx+c的自变量x与函数值y的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是
.
x
6.17
6.18
6.19
6.20
y=ax2+bx+c
﹣0.03
﹣0.01
0.02
0.04
10.在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是
.
三.解答题(共2小题)
11.如图,开口向下的抛物线与x轴交于点A(﹣1,0)、B(2,0),与y轴交于点C(0,4),点P是第一象限内抛物线上的一点.
(1)求该抛物线所对应的函数解析式;
(2)设四边形CABP的面积为S,求S的最大值.
12.画出函数y=﹣2x2+8x﹣6的图象,根据图象回答:
(1)方程﹣2x2+8x﹣6=0的解是什么;
(2)当x取何值时,y>0;
(3)当x取何值时,y<0.
22.2
二次函数与一元二次方程
参考答案与试题解析
一.选择题(共6小题)
1.已知二次函数y=﹣x2+2x+4,则下列关于这个函数图象和性质的说法,正确的是( )
A.图象的开口向上
B.图象的顶点坐标是(1,3)
C.当x<1时,y随x的增大而增大
D.图象与x轴有唯一交点
【分析】先利用配方法得到y=﹣(x﹣1)2+5,可根据二次函数的性质可对A、B、C进行判断;通过解方程﹣x2+2x+4=0可对D进行判断.
【解答】解:∵y=﹣x2+2x+4=﹣(x﹣1)2+5,
∴抛物线的开口向下,顶点坐标为(1,5),抛物线的对称轴为直线x=1,当x<1时,y随x的增大而增大,
令y=0,则﹣x2+2x+4=0,解方程解得x1=1+,x2=1﹣,
∴△=4﹣4×(﹣1)×4=20>0,
∴抛物线与x轴有两个交点.
故选:C.
【点评】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程根的判断.也考查了二次函数的性质.
2.在平面直角坐标系中,已知a≠b,设函数y=(x﹣a)(x﹣b)的图象与x轴有M个交点,函数y=(ax+1)(bx+1)的图形与x轴有N个交点,则( )
A.M=N﹣1或M=N+1
B.M=N﹣1或M=N+2
C.M=N或M=N+1
D.M=N或M=N﹣1
【分析】解方程(x﹣a)(x﹣b)=0可判断抛物线y=(x﹣a)(x﹣b)与x轴有两个交点,则M=2,当y=0时,(ax+1)(bx+1)=0,讨论:当a≠0,b≠0或a=0,b≠0或b=0,a≠0可得到函数与x轴的交点个数,从而得到N的值,然后对各选项进行判断.
【解答】解:当y=0时,(x﹣a)(x﹣b)=0,解得x1=a,x2=b,抛物线y=(x﹣a)(x﹣b)与x轴的交点为(a,0),(b,0),
所以M=2,
当y=0时,(ax+1)(bx+1)=0,当a≠0,b≠0,解得x1=﹣,x2=﹣,抛物线y=(ax+1)(bx+1)与x轴的交点为(﹣,0),(﹣,0),此时N=2,
当a=0,b≠0,或b=0,a≠0时,函数y=(ax+1)(bx+1)为一次函数,则N=1,
所以M=N,M=N+1.
故选:C.
【点评】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了一次函数图象.
3.已知抛物线y=x2﹣x﹣1与x轴的一个交点为(m,0),则代数式﹣2m2+2m+2020的值为( )
A.2018
B.2019
C.2020
D.2021
【分析】将(m,0)代入抛物线表达式得:m2﹣m﹣1=0,即可求解.
【解答】解:将(m,0)代入抛物线表达式得:m2﹣m﹣1=0,
则﹣2m2+2m+2020=﹣2(m2﹣m)+2020=﹣2+2020=2018,
故选:A.
【点评】本题考查的是抛物线与x轴的交点,将点(m,0)代入函数表达式是解题的关键.
4.已知y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=2.若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两个根,且x1<x2,﹣1<x1<0,则下列说法正确的是( )
A.x1+x2<0
B.4<x2<5
C.b2﹣4ac<0
D.ab>0
【分析】利用函数图象分别得出抛物线与x轴交点的横坐标的关系,进而判断四个结论得出答案.
【解答】解:∵x1,x2是一元二次方程ax2+bx+c=0的两个根,
∴x1、x2是抛物线与x轴交点的横坐标,
∵抛物线的对称轴为x=2,
∴=2,即x1+x2=4>0,故选项A错误;
∵x1<x2,﹣1<x1<0,
∴﹣1<4﹣x2<0,
解得:4<x2<5,故选项B正确;
∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,故选项C错误;
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为x=2,
∴﹣=2,
∴b=﹣4a>0,
∴ab<0,故选项D错误;
故选:B.
【点评】主要考查二次函数与一元二次方程之间的关系,会利用对称轴的值求抛物线与x轴交点的横坐标间的数量关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.
5.二次函数y=﹣x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )
A.t>﹣5
B.﹣5<t<3
C.3<t≤4
D.﹣5<t≤4
【分析】如图,关于x的一元二次方程﹣x2+mx﹣t=0的解就是抛物线y=﹣x2+mx与直线y=t的交点的横坐标,利用图象法即可解决问题.
【解答】解:如图,关于x的一元二次方程﹣x2+mx﹣t=0的解就是抛物线y=﹣x2+mx与直线y=t的交点的横坐标,
当x=1时,y=3,
当x=5时,y=﹣5,
由图象可知关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,
直线y=t在直线y=﹣5和直线y=4之间包括直线y=4,
∴﹣5<t≤4.
故选:D.
【点评】本题考查抛物线与x轴的交点、一元二次方程等知识,解题的关键是学会利用图象法解决问题,画出图象是解决问题的关键,属于中考选择题中的压轴题.
6.表给出了二次函数y=ax2+bx+c(a≠0)的自变量x与函数值y的部分对应值:那么方程ax2+bx+c=0的一个根的近似值可能是( )
x
…
1
1.1
1.2
1.3
1.4
…
y
…
﹣1
﹣0.49
0.04
0.59
1.16
…
A.1.08
B.1.18
C.1.28
D.1.38
【分析】观察表中数据得到抛物线y=ax2+bx+c与x轴的一个交点在(1.1,0)和点(1.2,0)之间,更靠近点(1.2,0),然后根据抛物线与x轴的交点问题可得到方程ax2+bx+c=0一个根的近似值.
【解答】解:∵x=1.1时,y=ax2+bx+c=﹣0.49;x=1.2时,y=ax2+bx+c=0.04;
∴抛物线y=ax2+bx+c与x轴的一个交点在(1.1,0)和点(1.2,0)之间,更靠近点(1.2,0),
∴方程ax2+bx+c=0有一个根约为1.2.
故选:B.
【点评】本题考查了图象法求一元二次方程的近似根:通过表中数据确定抛物线与x轴的交点横坐标的范围,从而得到一元二次方程的根(由于作图或观察存在误差,由图象求得的根一般是近似的).
二.填空题(共4小题)
7.已知抛物线y=x2+bx+c的部分图象如图所示,当y<0时,x的取值范围是 ﹣1<x<3 .
【分析】根据函数图象和二次函数的性质,可以得到该抛物线与x轴的另一个交点,从而可以得到当y<0时,x的取值范围.
【解答】解:由图象可得,
该抛物线的对称轴为直线x=1,与x轴的一个交点为(﹣1,0),
故抛物线与x轴的另一个交点为(3,0),
故当y<0时,x的取值范围是﹣1<x<3.
【点评】本题考查抛物线与x轴的交点、二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质和数形结合的思想解答.
8.若关于x的函数y=kx2+2x﹣与x轴仅有一个交点,则实数k的值为 0或﹣ .
【分析】讨论:当k=0时,函数为一次函数y=2x﹣,满足条件;当k≠0时,根据判别式的意义得到△=22﹣4k×(﹣)=0,解方程得k的值.
【解答】解:当k=0时,函数为一次函数y=2x﹣,此函数与x轴只有一个交点;
当k≠0时,∵二次函数y=kx2+2x﹣与x轴仅有一个交点,
∴△=22﹣4k×(﹣)=0,解得k=﹣,
综上所述,实数k的值为0或﹣.
故答案为0或﹣.
【点评】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程;△=b2﹣4ac决定抛物线与x轴的交点个数.
9.根据下列表格中y=ax2+bx+c的自变量x与函数值y的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是 6.18<x<6.19 .
x
6.17
6.18
6.19
6.20
y=ax2+bx+c
﹣0.03
﹣0.01
0.02
0.04
【分析】利用二次函数和一元二次方程的性质.
【解答】解:由表格中的数据看出﹣0.01和0.02更接近于0,故x应取对应的范围.
故答案为:6.18<x<6.19.
【点评】本题考查了用图象法求一元二次方程的近似根,解题的关键是找到y由正变为负时,自变量的取值即可.
10.在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是 ﹣1<x2<0 .
【分析】利用对称轴及二次函数的图象性质,可以把图象与x轴另一个交点的取值范围确定.
【解答】解:由图象可知x=2时,y<0;x=3时,y>0;
由于直线x=1是它的对称轴,则由二次函数图象的对称性可知:x=0时,y<0;x=﹣1时,y>0;
所以另一个根x2的取值范围为﹣1<x2<0.
故答案为:﹣1<x2<0.
【点评】本题考查了图象法求一元二次方程的近似根,根据图象信息确定出图象与x轴交点的位置是解题的关键.
三.解答题(共2小题)
11.如图,开口向下的抛物线与x轴交于点A(﹣1,0)、B(2,0),与y轴交于点C(0,4),点P是第一象限内抛物线上的一点.
(1)求该抛物线所对应的函数解析式;
(2)设四边形CABP的面积为S,求S的最大值.
【分析】(1)设二次函数表达式为y=a(x+1)(x﹣2),再将点C代入,求出a值即可;
(2)连接OP,设点P坐标为(m,﹣2m2+2m+4),m>0,利用S四边形CABP=S△OAC+S△OCP+S△OPB得出S关于m的表达式,再求最值即可.
【解答】解:(1)∵A(﹣1,0),B(2,0),C(0,4),
设抛物线表达式为:y=a(x+1)(x﹣2),
将C代入得:4=﹣2a,
解得:a=﹣2,
∴该抛物线的解析式为:y=﹣2(x+1)(x﹣2)=﹣2x2+2x+4;
(2)连接OP,设点P坐标为(m,﹣2m2+2m+4),m>0,
∵A(﹣1,0),B(2,0),C(0,4),
可得:OA=1,OC=4,OB=2,
∴S=S四边形CABP=S△OAC+S△OCP+S△OPB
=×1×4+×4m+×2×(﹣2m2+2m+4)
=﹣2m2+4m+6
=﹣2(m﹣1)2+8,
当m=1时,S最大,最大值为8.
【点评】本题考查了二次函数的应用,待定系数法求二次函数表达式,解题的关键是能将四边形CABP的面积表示出来.
12.画出函数y=﹣2x2+8x﹣6的图象,根据图象回答:
(1)方程﹣2x2+8x﹣6=0的解是什么;
(2)当x取何值时,y>0;
(3)当x取何值时,y<0.
【分析】利用描点连线的方法画出函数y=﹣2x2+8x﹣6的图象.再根据图象判断函数的增减性.
【解答】解:函数y=﹣2x2+8x﹣6的图象如图.由图象可知:
(1)方程﹣2x2+8x﹣6=0的解x1=1,x2=3.
(2)当1<x<3时,y>0.
(3)当x<1或x>3时,y<0.
【点评】本题重点考查了函数图象的画法及解读.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/8
10:03:57;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
同课章节目录
