23.2 中心对称同步练习(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
23.2
中心对称
一.选择题(共9小题)
1.如图,菱形ABCD的对角线AC、BD交于点O,AC=4,BD=16,将△BOC绕着点C旋转180°得到△B′O′C′,则点A与点B′之间的距离为( )
A.6
B.8
C.10
D.12
2.如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A.平行四边形→正方形→平行四边形→矩形
B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→菱形→正方形→矩形
3.在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣3,1),B(﹣1,﹣1),C(3,﹣1),把△ABC绕着一点旋转180°得到△CDA,则点D的坐标为( )
A.(1,1)
B.(1,﹣1)
C.(3,1)
D.(﹣3,﹣1)
4.下列图形中不是中心对称图形的是( )
A.
B.
C.
D.
5.下列图形中,是中心对称图形的是( )
A.
B.
C.
D.
6.下列图形中,是轴对称图形,但不是中心对称图形的是( )
A.
B.
C.
D.
7.已知A点坐标为(﹣4,5),将点A向右平移5个单位,再向下平移8个单位,得到点A1,再作点A1关于原点的对称点A2,则A2坐标为( )
A.(﹣1,3)
B.(1,﹣3)
C.(9,8)
D.(﹣9,﹣8)
8.如图,在平面直角坐标系内,Rt△ABC的点A在第一象限,点B与点A关于原点对称,∠C=90°.AC与x轴交于点D,点E在x轴上,CD=2AD.若AD平分∠OAE,△ADE的面积为1,则△ABC的面积为( )
A.6
B.9
C.12
D.15
9.若点A(n,2)与点B(﹣3,m)关于原点对称,则n﹣m=( )
A.﹣1
B.﹣5
C.1
D.5
二.填空题(共6小题)
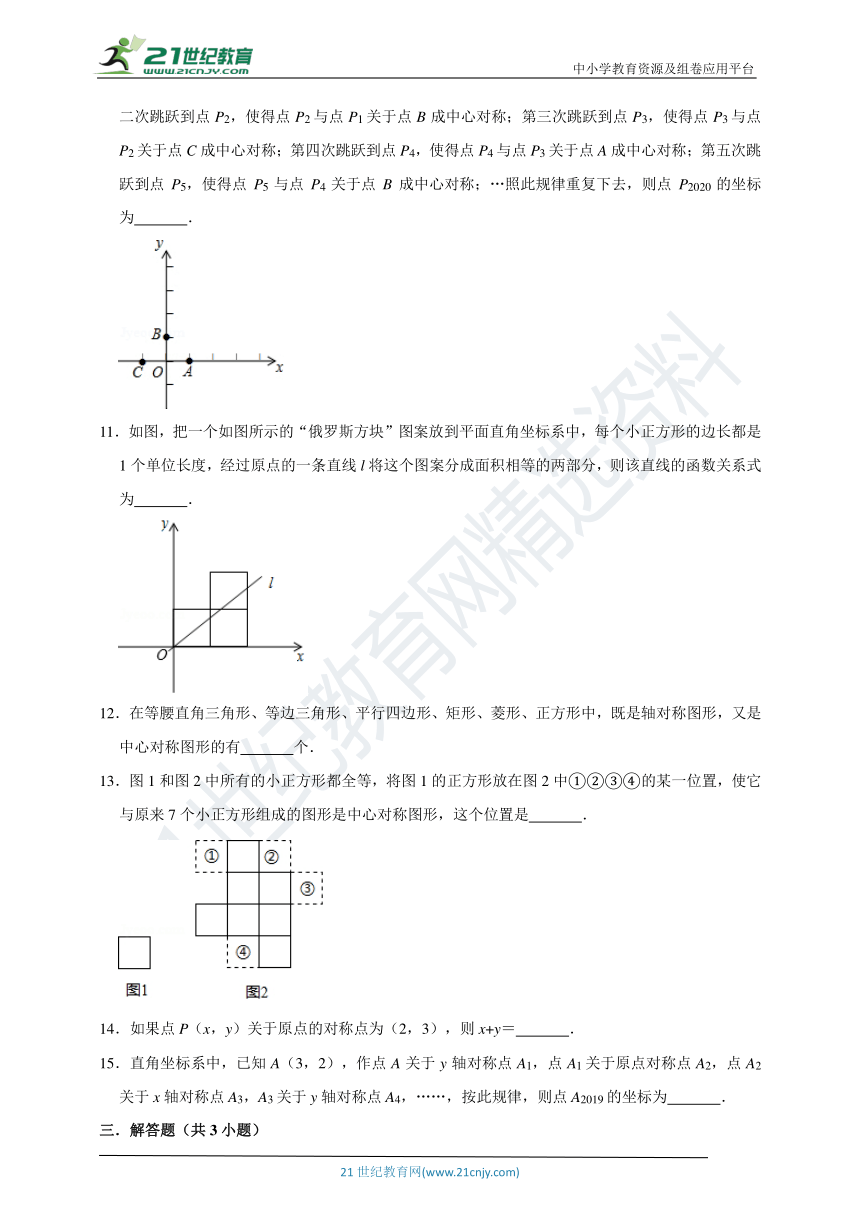
10.如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(﹣1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P2020的坐标为
.
11.如图,把一个如图所示的“俄罗斯方块”图案放到平面直角坐标系中,每个小正方形的边长都是1个单位长度,经过原点的一条直线l将这个图案分成面积相等的两部分,则该直线的函数关系式为
.
12.在等腰直角三角形、等边三角形、平行四边形、矩形、菱形、正方形中,既是轴对称图形,又是中心对称图形的有
个.
13.图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是
.
14.如果点P(x,y)关于原点的对称点为(2,3),则x+y=
.
15.直角坐标系中,已知A(3,2),作点A关于y轴对称点A1,点A1关于原点对称点A2,点A2关于x轴对称点A3,A3关于y轴对称点A4,……,按此规律,则点A2019的坐标为
.
三.解答题(共3小题)
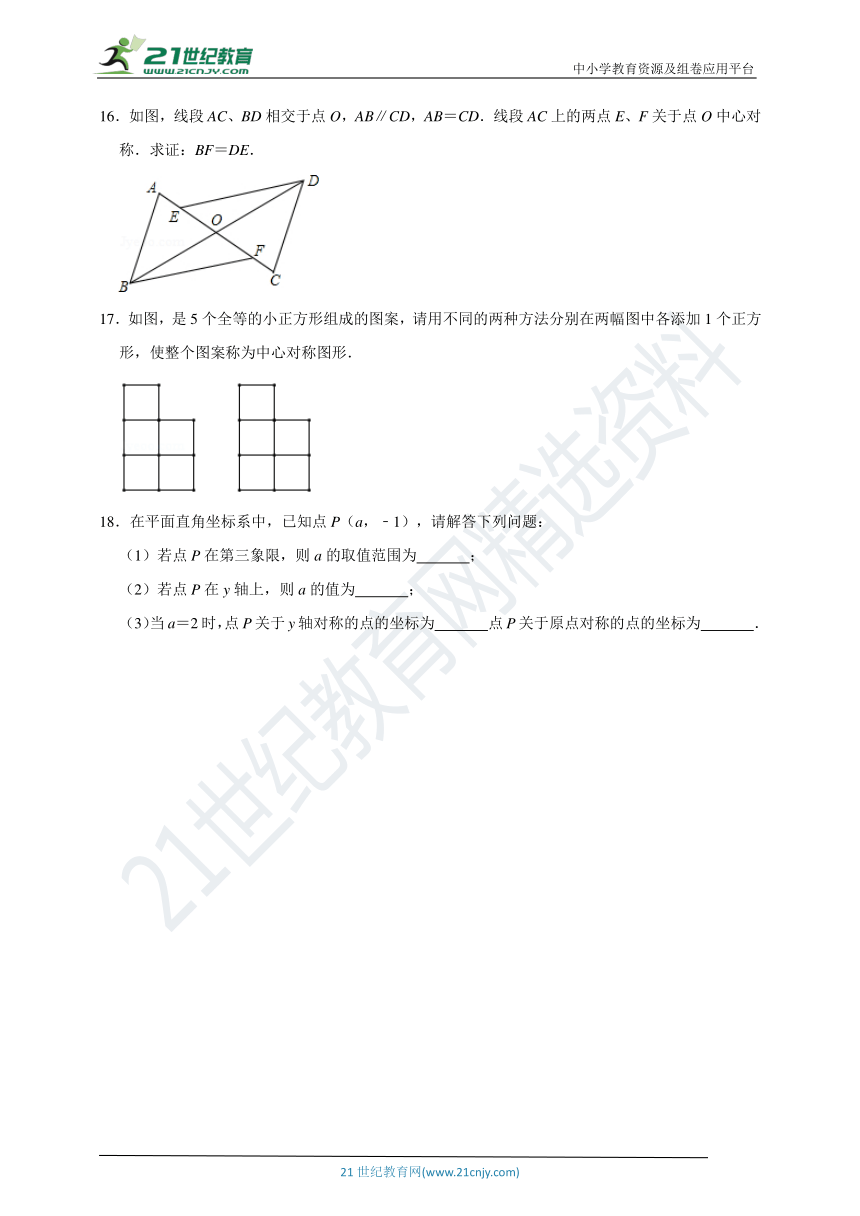
16.如图,线段AC、BD相交于点O,AB∥CD,AB=CD.线段AC上的两点E、F关于点O中心对称.求证:BF=DE.
17.如图,是5个全等的小正方形组成的图案,请用不同的两种方法分别在两幅图中各添加1个正方形,使整个图案称为中心对称图形.
18.在平面直角坐标系中,已知点P(a,﹣1),请解答下列问题:
(1)若点P在第三象限,则a的取值范围为
;
(2)若点P在y轴上,则a的值为
;
(3)当a=2时,点P关于y轴对称的点的坐标为
点P关于原点对称的点的坐标为
.
23.2
中心对称
参考答案与试题解析
一.选择题(共9小题)
1.如图,菱形ABCD的对角线AC、BD交于点O,AC=4,BD=16,将△BOC绕着点C旋转180°得到△B′O′C′,则点A与点B′之间的距离为( )
A.6
B.8
C.10
D.12
【分析】根据菱形ABCD的对角线AC、BD交于点O,AC=4,BD=16,可得AC⊥BD,所以∠BOC=90°,根据△BOC绕着点C旋转180°得到△B′O′C,所以∠CO′B′=∠BOC=90°,AO′=6,OB′=8,再根据勾股定理即可求出点A与点B′之间的距离.
【解答】解:∵菱形ABCD的对角线AC、BD交于点O,AC=4,BD=16,
∴AC⊥BD,
∴∠BOC=90°,
∵△BOC绕着点C旋转180°得到△B′O′C,
∴∠CO′B′=∠BOC=90°,
∴O′C=OC=OA=AC=2,
∴AO′=6,
∵OB=OD=OB′=BD=8,
在Rt△AO′B′中,根据勾股定理,得
AB′==10.
则点A与点B′之间的距离为10.
故选:C.
【点评】本题考查了中心对称、旋转的性质,解决本题的关键是掌握旋转的性质.
2.如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A.平行四边形→正方形→平行四边形→矩形
B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→菱形→正方形→矩形
【分析】根据对称中心的定义,根据矩形的性质,可得四边形AECF形状的变化情况.
【解答】解:观察图形可知,四边形AECF形状的变化依次为平行四边形→菱形→平行四边形→矩形.
故选:B.
【点评】考查了中心对称,矩形的性质,平行四边形的判定与性质,菱形的判定,根据EF与AC的位置关系即可求解.
3.在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣3,1),B(﹣1,﹣1),C(3,﹣1),把△ABC绕着一点旋转180°得到△CDA,则点D的坐标为( )
A.(1,1)
B.(1,﹣1)
C.(3,1)
D.(﹣3,﹣1)
【分析】根据题意可得A(﹣3,1)与C(3,﹣1),关于原点对称,旋转中心是原点,可得B(﹣1,﹣1)与D关于原点对称,即可求出点D的坐标.
【解答】解:A(﹣3,1)与C(3,﹣1),关于原点对称,
∴旋转中心是原点,
∴B(﹣1,﹣1)与D关于原点对称,
∴D(1,1).
故选:A.
【点评】本题考查了中心对称、坐标与图形变化﹣旋转,解决本题的关键是掌握中心对称的定义.
4.下列图形中不是中心对称图形的是( )
A.
B.
C.
D.
【分析】根据中心对称图形的概念判断.
【解答】解:A、不是中心对称图形;
B、是中心对称图形;
C、是中心对称图形;
D、是中心对称图形;
故选:A.
【点评】本题考查的是中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
5.下列图形中,是中心对称图形的是( )
A.
B.
C.
D.
【分析】根据中心对称图形的概念判断即可.
【解答】解:A、是中心对称图形;
B、不是中心对称图形;
C、不是中心对称图形;
D、不是中心对称图形;
故选:A.
【点评】本题考查的是中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
6.下列图形中,是轴对称图形,但不是中心对称图形的是( )
A.
B.
C.
D.
【分析】根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解.
【解答】解:A、不是轴对称图形,是中心对称图形,故本选项错误;
B、不是轴对称图形,是中心对称图形,故本选项错误;
C、是轴对称图形,是中心对称图形,故本选项错误;
D、轴对称图形,但不是中心对称图形,故本选项正确.
故选:D.
【点评】本题考查了中心对称图形与轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
7.已知A点坐标为(﹣4,5),将点A向右平移5个单位,再向下平移8个单位,得到点A1,再作点A1关于原点的对称点A2,则A2坐标为( )
A.(﹣1,3)
B.(1,﹣3)
C.(9,8)
D.(﹣9,﹣8)
【分析】直接利用平移的性质得出点A1的坐标,进而利用关于原点对称点的性质得出答案.
【解答】解:∵A点坐标为(﹣4,5),将点A向右平移5个单位,再向下平移8个单位,得到点A1,
∴点A1的坐标为:(1,﹣3),
∵点A1关于原点的对称点A2,
∴A2坐标为(﹣1,3).
故选:A.
【点评】此题主要考查了平移变换以及关于原点对称点的性质,正确掌握点的平移规律是解题关键.
8.如图,在平面直角坐标系内,Rt△ABC的点A在第一象限,点B与点A关于原点对称,∠C=90°.AC与x轴交于点D,点E在x轴上,CD=2AD.若AD平分∠OAE,△ADE的面积为1,则△ABC的面积为( )
A.6
B.9
C.12
D.15
【分析】连接OC,根据直角三角形的性质可得OC=OA,进而得出∠OCD=∠OAD,根据角平分线的定义可得∠OAD=∠EAD,从而得出△ADE∽△CDO,易得ON=2EM,BC=2ON=4EM,再根据CD=2AD可得AC=3AD,所以△ABC的面积为△ADE的面积的面积的12倍.
【解答】解:如图,连接OC,作EM⊥AD于M,作ON⊥AC于N,
由点B与点A关于原点对称.可得OA=OB,
又∵△ABC是直角三角形,
∴OC=OA,
所以∠OCD=∠OAD,
∵AD平分∠OAE,
∴得∠OAD=∠EAD,
∴∠OAD=∠EAD,
又∵∠ADE=∠CDO,
∴△ADE∽△CDO,
∵CD=2AD,
∴ON=2EM,AC=3AD,
∴BC=2ON=4EM,
∴=.
故选:C.
【点评】本题主要考查了关于原点对称的点的坐标特点,直角三角形的性质,三角形的中位线定理,相似三角形的判断与性质等知识,综合性较强,得出△ADE∽△CDO是解答本题的关键.
9.若点A(n,2)与点B(﹣3,m)关于原点对称,则n﹣m=( )
A.﹣1
B.﹣5
C.1
D.5
【分析】直接利用关于原点对称点的性质得出m,n的值,进而得出答案.
【解答】解:∵点A(n,2)与点B(﹣3,m)关于原点对称,
∴n=3,m=﹣2,
∴n﹣m=3﹣(﹣2)=5.
故选:D.
【点评】此题主要考查了关于原点对称点的性质,正确掌握横纵坐标的关系是解题关键.
二.填空题(共6小题)
10.如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(﹣1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P2020的坐标为 (2,2) .
【分析】根据中心对称的性质找出部分Pn的坐标,根据坐标的变化找出变化规律“P6n(0,0),P6n+1(2,0),P6n+2(﹣2,2),P6n+3(0,﹣2),P6n+4(2,2),P6n+5(﹣2,0)(n为自然数)”,依此规律即可得出结论.
【解答】解:观察,发现规律:
P0(0,0),P1(2,0),P2(﹣2,2),P3(0,﹣2),P4(2,2),P5(﹣2,0),P6(0,0),P7(2,0),…,
∴P6n(0,0),P6n+1(2,0),P6n+2(﹣2,2),P6n+3(0,﹣2),P6n+4(2,2),P6n+5(﹣2,0)(n为自然数).
∵2020=6×336+4,
∴P2020(2,2).
故答案为:(2,2).
【点评】本题考查了规律型中的点的坐标以及中心对称的性质,解题的关键是找出变化规律“P6n(0,0),P6n+1(2,0),P6n+2(﹣2,2),P6n+3(0,﹣2),P6n+4(2,2),P6n+5(﹣2,0)(n为自然数)”.本题属于基础题,难度不大,解决该题型题目时,根据题意列出部分Pn点的坐标,根据坐标的变化找出变化规律是关键.
11.如图,把一个如图所示的“俄罗斯方块”图案放到平面直角坐标系中,每个小正方形的边长都是1个单位长度,经过原点的一条直线l将这个图案分成面积相等的两部分,则该直线的函数关系式为 y=x .
【分析】设直线l和俄罗斯方块交点为A,易知OB=2,利用三角形的面积公式和已知条件求出A的坐标即可得到该直线l的解析式.
【解答】解:设直线l与俄罗斯方块交于点A.
∵直线l将这个图案分成面积相等的两部分,
∴S△OAB==,
即=,
×2×AB=,
AB=,
∴A(2,),
设直线l解析式y=kx,
将A(2,)代入,得=2k,
解得k=,
∴该直线的函数关系式为y=x,
故答案为y=x.
【点评】此题考查了面积相等问题、用待定系数法求一次函数的解析式以及正方形的性质,此题难度较大,解题的关利用三角形的面积公式求出AB的长.
12.在等腰直角三角形、等边三角形、平行四边形、矩形、菱形、正方形中,既是轴对称图形,又是中心对称图形的有 3 个.
【分析】根据轴对称图形与中心对称图形的概念求解.
【解答】解:由题可得,既是轴对称图形,又是中心对称图形的有3个:矩形、菱形、正方形,
故答案为:3.
【点评】此题主要考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
13.图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是 ③ .
【分析】根据把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心,进而得出答案.
【解答】解:当正方形放在③的位置,即是中心对称图形.
故答案为:③.
【点评】此题主要考查了中心对称图形的定义,正确把握定义是解题关键.
14.如果点P(x,y)关于原点的对称点为(2,3),则x+y= ﹣5 .
【分析】平面直角坐标系中任意一点P(x,y),关于原点的对称点是(﹣x,﹣y),记忆方法是结合平面直角坐标系的图形记忆.
【解答】解:∵点P(x,y)关于原点的对称点为(2,3),
∴x=﹣2,y=﹣3;
∴x+y=﹣2﹣3=﹣5.
故答案是:﹣5.
【点评】此题主要考查了关于原点对称的点的坐标特点,关键是掌握点的坐标的变化规律.
15.直角坐标系中,已知A(3,2),作点A关于y轴对称点A1,点A1关于原点对称点A2,点A2关于x轴对称点A3,A3关于y轴对称点A4,……,按此规律,则点A2019的坐标为 (3,2) .
【分析】此题主要是发现循环的规律,然后根据规律进行计算.
【解答】解:作点A关于y轴的对称点为A1,是(﹣3,2);
作点A1关于原点的对称点为A2,是(3,﹣2);
作点A2关于x轴的对称点为A3,是(3,2).
显然此为一循环,按此规律,2019÷3=673,
则点A2019的坐标是(3,2),
故答案为:(3,2).
【点评】本题考查了关于原点对称的点的坐标,关于坐标轴对称点的坐标,解答此题需熟悉:两个点关于x轴对称,则横坐标不变,纵坐标互为相反数;两个点关于y轴对称,则横坐标互为相反数,纵坐标不变;两个点关于原点对称,则横坐标、纵坐标都是互为相反数.
三.解答题(共3小题)
16.如图,线段AC、BD相交于点O,AB∥CD,AB=CD.线段AC上的两点E、F关于点O中心对称.求证:BF=DE.
【分析】连接AD、BC,根据一组对边平行且相等的四边形是平行四边形证明四边形ABCD是平行四边形,再根据平行四边形的对角线互相平分可得BO=DO,根据E、F关于点O中心对称可得OE=OF,然后利用“边角边”证明△BOF和△DOE全等,根据全等三角形对应边相等即可得证.
【解答】证明:如图,连接AD、BC,
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴BO=DO,
∵点E、F关于点O中心对称,
∴OF=OE,
在△BOF和△DOE中,,
∴△BOF≌△DOE(SAS),
∴BF=DE.
【点评】本题考查了中心对称的性质,全等三角形的判定与性质,平行四边形的判定与性质,作辅助线构造出平行四边形,然后证明得到BO=DO是证明三角形全等的关键,也是解决本题的难点.
17.如图,是5个全等的小正方形组成的图案,请用不同的两种方法分别在两幅图中各添加1个正方形,使整个图案称为中心对称图形.
【分析】直接利用中心对称图形的定义进而分析得出答案.
【解答】解:如图所示:
.
【点评】此题主要考查了中心对称图形,正确把握中心对称图形的定义是解题关键.
18.在平面直角坐标系中,已知点P(a,﹣1),请解答下列问题:
(1)若点P在第三象限,则a的取值范围为 a<0 ;
(2)若点P在y轴上,则a的值为 0 ;
(3)当a=2时,点P关于y轴对称的点的坐标为 (﹣2,﹣1) 点P关于原点对称的点的坐标为 (﹣2,1) .
【分析】(1)直接利用第三象限内点的坐标特点得出答案;
(2)直接利用y轴上点的坐标特点得出a的值;
(3)利用关于y轴以及关于原点对称点的性质得出答案.
【解答】解:(1)∵点P(a,﹣1),点P在第三象限,
∴a<0;
故答案为:a<0;
(2)∵点P(a,﹣1),点P在y轴上,
∴a=0;
故答案为:0;
(3)当a=2时,点P(a,﹣1)的坐标为:(2,﹣1)关于y轴对称的点的坐标为:(﹣2,﹣1),
点P关于原点对称的点的坐标为:(﹣2,1).
故答案为:(﹣2,﹣1),(﹣2,1).
【点评】此题主要考查了关于y轴对称以及关于原点对称点的性质,正确掌握各象限内点的坐标特点是解题关键.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/8
10:18:28;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
23.2
中心对称
一.选择题(共9小题)
1.如图,菱形ABCD的对角线AC、BD交于点O,AC=4,BD=16,将△BOC绕着点C旋转180°得到△B′O′C′,则点A与点B′之间的距离为( )
A.6
B.8
C.10
D.12
2.如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A.平行四边形→正方形→平行四边形→矩形
B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→菱形→正方形→矩形
3.在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣3,1),B(﹣1,﹣1),C(3,﹣1),把△ABC绕着一点旋转180°得到△CDA,则点D的坐标为( )
A.(1,1)
B.(1,﹣1)
C.(3,1)
D.(﹣3,﹣1)
4.下列图形中不是中心对称图形的是( )
A.
B.
C.
D.
5.下列图形中,是中心对称图形的是( )
A.
B.
C.
D.
6.下列图形中,是轴对称图形,但不是中心对称图形的是( )
A.
B.
C.
D.
7.已知A点坐标为(﹣4,5),将点A向右平移5个单位,再向下平移8个单位,得到点A1,再作点A1关于原点的对称点A2,则A2坐标为( )
A.(﹣1,3)
B.(1,﹣3)
C.(9,8)
D.(﹣9,﹣8)
8.如图,在平面直角坐标系内,Rt△ABC的点A在第一象限,点B与点A关于原点对称,∠C=90°.AC与x轴交于点D,点E在x轴上,CD=2AD.若AD平分∠OAE,△ADE的面积为1,则△ABC的面积为( )
A.6
B.9
C.12
D.15
9.若点A(n,2)与点B(﹣3,m)关于原点对称,则n﹣m=( )
A.﹣1
B.﹣5
C.1
D.5
二.填空题(共6小题)
10.如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(﹣1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P2020的坐标为
.
11.如图,把一个如图所示的“俄罗斯方块”图案放到平面直角坐标系中,每个小正方形的边长都是1个单位长度,经过原点的一条直线l将这个图案分成面积相等的两部分,则该直线的函数关系式为
.
12.在等腰直角三角形、等边三角形、平行四边形、矩形、菱形、正方形中,既是轴对称图形,又是中心对称图形的有
个.
13.图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是
.
14.如果点P(x,y)关于原点的对称点为(2,3),则x+y=
.
15.直角坐标系中,已知A(3,2),作点A关于y轴对称点A1,点A1关于原点对称点A2,点A2关于x轴对称点A3,A3关于y轴对称点A4,……,按此规律,则点A2019的坐标为
.
三.解答题(共3小题)
16.如图,线段AC、BD相交于点O,AB∥CD,AB=CD.线段AC上的两点E、F关于点O中心对称.求证:BF=DE.
17.如图,是5个全等的小正方形组成的图案,请用不同的两种方法分别在两幅图中各添加1个正方形,使整个图案称为中心对称图形.
18.在平面直角坐标系中,已知点P(a,﹣1),请解答下列问题:
(1)若点P在第三象限,则a的取值范围为
;
(2)若点P在y轴上,则a的值为
;
(3)当a=2时,点P关于y轴对称的点的坐标为
点P关于原点对称的点的坐标为
.
23.2
中心对称
参考答案与试题解析
一.选择题(共9小题)
1.如图,菱形ABCD的对角线AC、BD交于点O,AC=4,BD=16,将△BOC绕着点C旋转180°得到△B′O′C′,则点A与点B′之间的距离为( )
A.6
B.8
C.10
D.12
【分析】根据菱形ABCD的对角线AC、BD交于点O,AC=4,BD=16,可得AC⊥BD,所以∠BOC=90°,根据△BOC绕着点C旋转180°得到△B′O′C,所以∠CO′B′=∠BOC=90°,AO′=6,OB′=8,再根据勾股定理即可求出点A与点B′之间的距离.
【解答】解:∵菱形ABCD的对角线AC、BD交于点O,AC=4,BD=16,
∴AC⊥BD,
∴∠BOC=90°,
∵△BOC绕着点C旋转180°得到△B′O′C,
∴∠CO′B′=∠BOC=90°,
∴O′C=OC=OA=AC=2,
∴AO′=6,
∵OB=OD=OB′=BD=8,
在Rt△AO′B′中,根据勾股定理,得
AB′==10.
则点A与点B′之间的距离为10.
故选:C.
【点评】本题考查了中心对称、旋转的性质,解决本题的关键是掌握旋转的性质.
2.如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A.平行四边形→正方形→平行四边形→矩形
B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→菱形→正方形→矩形
【分析】根据对称中心的定义,根据矩形的性质,可得四边形AECF形状的变化情况.
【解答】解:观察图形可知,四边形AECF形状的变化依次为平行四边形→菱形→平行四边形→矩形.
故选:B.
【点评】考查了中心对称,矩形的性质,平行四边形的判定与性质,菱形的判定,根据EF与AC的位置关系即可求解.
3.在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣3,1),B(﹣1,﹣1),C(3,﹣1),把△ABC绕着一点旋转180°得到△CDA,则点D的坐标为( )
A.(1,1)
B.(1,﹣1)
C.(3,1)
D.(﹣3,﹣1)
【分析】根据题意可得A(﹣3,1)与C(3,﹣1),关于原点对称,旋转中心是原点,可得B(﹣1,﹣1)与D关于原点对称,即可求出点D的坐标.
【解答】解:A(﹣3,1)与C(3,﹣1),关于原点对称,
∴旋转中心是原点,
∴B(﹣1,﹣1)与D关于原点对称,
∴D(1,1).
故选:A.
【点评】本题考查了中心对称、坐标与图形变化﹣旋转,解决本题的关键是掌握中心对称的定义.
4.下列图形中不是中心对称图形的是( )
A.
B.
C.
D.
【分析】根据中心对称图形的概念判断.
【解答】解:A、不是中心对称图形;
B、是中心对称图形;
C、是中心对称图形;
D、是中心对称图形;
故选:A.
【点评】本题考查的是中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
5.下列图形中,是中心对称图形的是( )
A.
B.
C.
D.
【分析】根据中心对称图形的概念判断即可.
【解答】解:A、是中心对称图形;
B、不是中心对称图形;
C、不是中心对称图形;
D、不是中心对称图形;
故选:A.
【点评】本题考查的是中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
6.下列图形中,是轴对称图形,但不是中心对称图形的是( )
A.
B.
C.
D.
【分析】根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解.
【解答】解:A、不是轴对称图形,是中心对称图形,故本选项错误;
B、不是轴对称图形,是中心对称图形,故本选项错误;
C、是轴对称图形,是中心对称图形,故本选项错误;
D、轴对称图形,但不是中心对称图形,故本选项正确.
故选:D.
【点评】本题考查了中心对称图形与轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
7.已知A点坐标为(﹣4,5),将点A向右平移5个单位,再向下平移8个单位,得到点A1,再作点A1关于原点的对称点A2,则A2坐标为( )
A.(﹣1,3)
B.(1,﹣3)
C.(9,8)
D.(﹣9,﹣8)
【分析】直接利用平移的性质得出点A1的坐标,进而利用关于原点对称点的性质得出答案.
【解答】解:∵A点坐标为(﹣4,5),将点A向右平移5个单位,再向下平移8个单位,得到点A1,
∴点A1的坐标为:(1,﹣3),
∵点A1关于原点的对称点A2,
∴A2坐标为(﹣1,3).
故选:A.
【点评】此题主要考查了平移变换以及关于原点对称点的性质,正确掌握点的平移规律是解题关键.
8.如图,在平面直角坐标系内,Rt△ABC的点A在第一象限,点B与点A关于原点对称,∠C=90°.AC与x轴交于点D,点E在x轴上,CD=2AD.若AD平分∠OAE,△ADE的面积为1,则△ABC的面积为( )
A.6
B.9
C.12
D.15
【分析】连接OC,根据直角三角形的性质可得OC=OA,进而得出∠OCD=∠OAD,根据角平分线的定义可得∠OAD=∠EAD,从而得出△ADE∽△CDO,易得ON=2EM,BC=2ON=4EM,再根据CD=2AD可得AC=3AD,所以△ABC的面积为△ADE的面积的面积的12倍.
【解答】解:如图,连接OC,作EM⊥AD于M,作ON⊥AC于N,
由点B与点A关于原点对称.可得OA=OB,
又∵△ABC是直角三角形,
∴OC=OA,
所以∠OCD=∠OAD,
∵AD平分∠OAE,
∴得∠OAD=∠EAD,
∴∠OAD=∠EAD,
又∵∠ADE=∠CDO,
∴△ADE∽△CDO,
∵CD=2AD,
∴ON=2EM,AC=3AD,
∴BC=2ON=4EM,
∴=.
故选:C.
【点评】本题主要考查了关于原点对称的点的坐标特点,直角三角形的性质,三角形的中位线定理,相似三角形的判断与性质等知识,综合性较强,得出△ADE∽△CDO是解答本题的关键.
9.若点A(n,2)与点B(﹣3,m)关于原点对称,则n﹣m=( )
A.﹣1
B.﹣5
C.1
D.5
【分析】直接利用关于原点对称点的性质得出m,n的值,进而得出答案.
【解答】解:∵点A(n,2)与点B(﹣3,m)关于原点对称,
∴n=3,m=﹣2,
∴n﹣m=3﹣(﹣2)=5.
故选:D.
【点评】此题主要考查了关于原点对称点的性质,正确掌握横纵坐标的关系是解题关键.
二.填空题(共6小题)
10.如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(﹣1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P2020的坐标为 (2,2) .
【分析】根据中心对称的性质找出部分Pn的坐标,根据坐标的变化找出变化规律“P6n(0,0),P6n+1(2,0),P6n+2(﹣2,2),P6n+3(0,﹣2),P6n+4(2,2),P6n+5(﹣2,0)(n为自然数)”,依此规律即可得出结论.
【解答】解:观察,发现规律:
P0(0,0),P1(2,0),P2(﹣2,2),P3(0,﹣2),P4(2,2),P5(﹣2,0),P6(0,0),P7(2,0),…,
∴P6n(0,0),P6n+1(2,0),P6n+2(﹣2,2),P6n+3(0,﹣2),P6n+4(2,2),P6n+5(﹣2,0)(n为自然数).
∵2020=6×336+4,
∴P2020(2,2).
故答案为:(2,2).
【点评】本题考查了规律型中的点的坐标以及中心对称的性质,解题的关键是找出变化规律“P6n(0,0),P6n+1(2,0),P6n+2(﹣2,2),P6n+3(0,﹣2),P6n+4(2,2),P6n+5(﹣2,0)(n为自然数)”.本题属于基础题,难度不大,解决该题型题目时,根据题意列出部分Pn点的坐标,根据坐标的变化找出变化规律是关键.
11.如图,把一个如图所示的“俄罗斯方块”图案放到平面直角坐标系中,每个小正方形的边长都是1个单位长度,经过原点的一条直线l将这个图案分成面积相等的两部分,则该直线的函数关系式为 y=x .
【分析】设直线l和俄罗斯方块交点为A,易知OB=2,利用三角形的面积公式和已知条件求出A的坐标即可得到该直线l的解析式.
【解答】解:设直线l与俄罗斯方块交于点A.
∵直线l将这个图案分成面积相等的两部分,
∴S△OAB==,
即=,
×2×AB=,
AB=,
∴A(2,),
设直线l解析式y=kx,
将A(2,)代入,得=2k,
解得k=,
∴该直线的函数关系式为y=x,
故答案为y=x.
【点评】此题考查了面积相等问题、用待定系数法求一次函数的解析式以及正方形的性质,此题难度较大,解题的关利用三角形的面积公式求出AB的长.
12.在等腰直角三角形、等边三角形、平行四边形、矩形、菱形、正方形中,既是轴对称图形,又是中心对称图形的有 3 个.
【分析】根据轴对称图形与中心对称图形的概念求解.
【解答】解:由题可得,既是轴对称图形,又是中心对称图形的有3个:矩形、菱形、正方形,
故答案为:3.
【点评】此题主要考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
13.图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是 ③ .
【分析】根据把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心,进而得出答案.
【解答】解:当正方形放在③的位置,即是中心对称图形.
故答案为:③.
【点评】此题主要考查了中心对称图形的定义,正确把握定义是解题关键.
14.如果点P(x,y)关于原点的对称点为(2,3),则x+y= ﹣5 .
【分析】平面直角坐标系中任意一点P(x,y),关于原点的对称点是(﹣x,﹣y),记忆方法是结合平面直角坐标系的图形记忆.
【解答】解:∵点P(x,y)关于原点的对称点为(2,3),
∴x=﹣2,y=﹣3;
∴x+y=﹣2﹣3=﹣5.
故答案是:﹣5.
【点评】此题主要考查了关于原点对称的点的坐标特点,关键是掌握点的坐标的变化规律.
15.直角坐标系中,已知A(3,2),作点A关于y轴对称点A1,点A1关于原点对称点A2,点A2关于x轴对称点A3,A3关于y轴对称点A4,……,按此规律,则点A2019的坐标为 (3,2) .
【分析】此题主要是发现循环的规律,然后根据规律进行计算.
【解答】解:作点A关于y轴的对称点为A1,是(﹣3,2);
作点A1关于原点的对称点为A2,是(3,﹣2);
作点A2关于x轴的对称点为A3,是(3,2).
显然此为一循环,按此规律,2019÷3=673,
则点A2019的坐标是(3,2),
故答案为:(3,2).
【点评】本题考查了关于原点对称的点的坐标,关于坐标轴对称点的坐标,解答此题需熟悉:两个点关于x轴对称,则横坐标不变,纵坐标互为相反数;两个点关于y轴对称,则横坐标互为相反数,纵坐标不变;两个点关于原点对称,则横坐标、纵坐标都是互为相反数.
三.解答题(共3小题)
16.如图,线段AC、BD相交于点O,AB∥CD,AB=CD.线段AC上的两点E、F关于点O中心对称.求证:BF=DE.
【分析】连接AD、BC,根据一组对边平行且相等的四边形是平行四边形证明四边形ABCD是平行四边形,再根据平行四边形的对角线互相平分可得BO=DO,根据E、F关于点O中心对称可得OE=OF,然后利用“边角边”证明△BOF和△DOE全等,根据全等三角形对应边相等即可得证.
【解答】证明:如图,连接AD、BC,
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴BO=DO,
∵点E、F关于点O中心对称,
∴OF=OE,
在△BOF和△DOE中,,
∴△BOF≌△DOE(SAS),
∴BF=DE.
【点评】本题考查了中心对称的性质,全等三角形的判定与性质,平行四边形的判定与性质,作辅助线构造出平行四边形,然后证明得到BO=DO是证明三角形全等的关键,也是解决本题的难点.
17.如图,是5个全等的小正方形组成的图案,请用不同的两种方法分别在两幅图中各添加1个正方形,使整个图案称为中心对称图形.
【分析】直接利用中心对称图形的定义进而分析得出答案.
【解答】解:如图所示:
.
【点评】此题主要考查了中心对称图形,正确把握中心对称图形的定义是解题关键.
18.在平面直角坐标系中,已知点P(a,﹣1),请解答下列问题:
(1)若点P在第三象限,则a的取值范围为 a<0 ;
(2)若点P在y轴上,则a的值为 0 ;
(3)当a=2时,点P关于y轴对称的点的坐标为 (﹣2,﹣1) 点P关于原点对称的点的坐标为 (﹣2,1) .
【分析】(1)直接利用第三象限内点的坐标特点得出答案;
(2)直接利用y轴上点的坐标特点得出a的值;
(3)利用关于y轴以及关于原点对称点的性质得出答案.
【解答】解:(1)∵点P(a,﹣1),点P在第三象限,
∴a<0;
故答案为:a<0;
(2)∵点P(a,﹣1),点P在y轴上,
∴a=0;
故答案为:0;
(3)当a=2时,点P(a,﹣1)的坐标为:(2,﹣1)关于y轴对称的点的坐标为:(﹣2,﹣1),
点P关于原点对称的点的坐标为:(﹣2,1).
故答案为:(﹣2,﹣1),(﹣2,1).
【点评】此题主要考查了关于y轴对称以及关于原点对称点的性质,正确掌握各象限内点的坐标特点是解题关键.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/8
10:18:28;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
同课章节目录
