24.2.2 直线和圆的位置关系(1)同步练习(含解析)
文档属性
| 名称 | 24.2.2 直线和圆的位置关系(1)同步练习(含解析) |  | |
| 格式 | rar | ||
| 文件大小 | 560.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 21:10:22 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
24.2.2
直线和圆的位置关系(1)
一.选择题(共9小题)
1.平面直角坐标系中,⊙P的圆心坐标为(﹣4,﹣5),半径为5,那么⊙P与y轴的位置关系是( )
A.相交
B.相离
C.相切
D.以上都不是
2.已知⊙O的半径为7,直线l与⊙O相交,点O到直线l的距离为4,则⊙O上到直线l的距离为3的点共有( )
A.1个
B.2个
C.3个
D.4个
3.已知线段AB=2,点A,B到直线l的距离分别为方程x2﹣6x+6=0的两根,符合条件的直线l有( )
A.1条
B.2条
C.3条
D.4条
4.如图,以矩形ABCD对角线BD上一点O为圆心作⊙O过A点并与CD切于E点,若CD=3,BC=5,则⊙O的半径为( )
A.
B.3
C.
D.
5.如图,AB是⊙O的弦,AC与⊙O相切于点A,连接OA,OB,若∠O=130°,则∠BAC的度数是( )
A.60°
B.65°
C.70°
D.75°
6.如图,△ABC内接于圆,∠ACB=90°,过点C的切线交AB的延长线于点P,∠P=28°.则∠CAB=( )
A.62°
B.31°
C.28°
D.56°
7.如图,在平面直角坐标系中,过格点A,B,C画圆弧,则点B与下列格点连线所得的直线中,能够与该圆弧相切的格点坐标是( )
A.(5,2)
B.(2,4)
C.(1,4)
D.(6,2)
8.如图,点D是△ABC中BC边的中点,DE⊥AC于E,以AB为直径的⊙O经过D,连接AD,有下列结论:①AD⊥BC;②∠EDA=∠B;③OA=AC;④DE是⊙O的切线.其中正确的结论是( )
A.①②
B.①②③
C.②③
D.①②③④
9.已知在矩形ABCD中,AB=5,对角线AC=13.⊙C的半径长为12,下列说法正确的是( )
A.⊙C与直线AB相交
B.⊙C与直线AD相切
C.点A在⊙C上
D.点D在⊙C内
二.填空题(共6小题)
10.⊙O的半径为4,圆心O到直线l的距离为2,则直线l与⊙O的位置关系是
.
11.直线y=kx+6k交x轴于点A,交y轴于点B,以原点O为圆心,3为半径的⊙O与l相交,则k的取值范围为
.
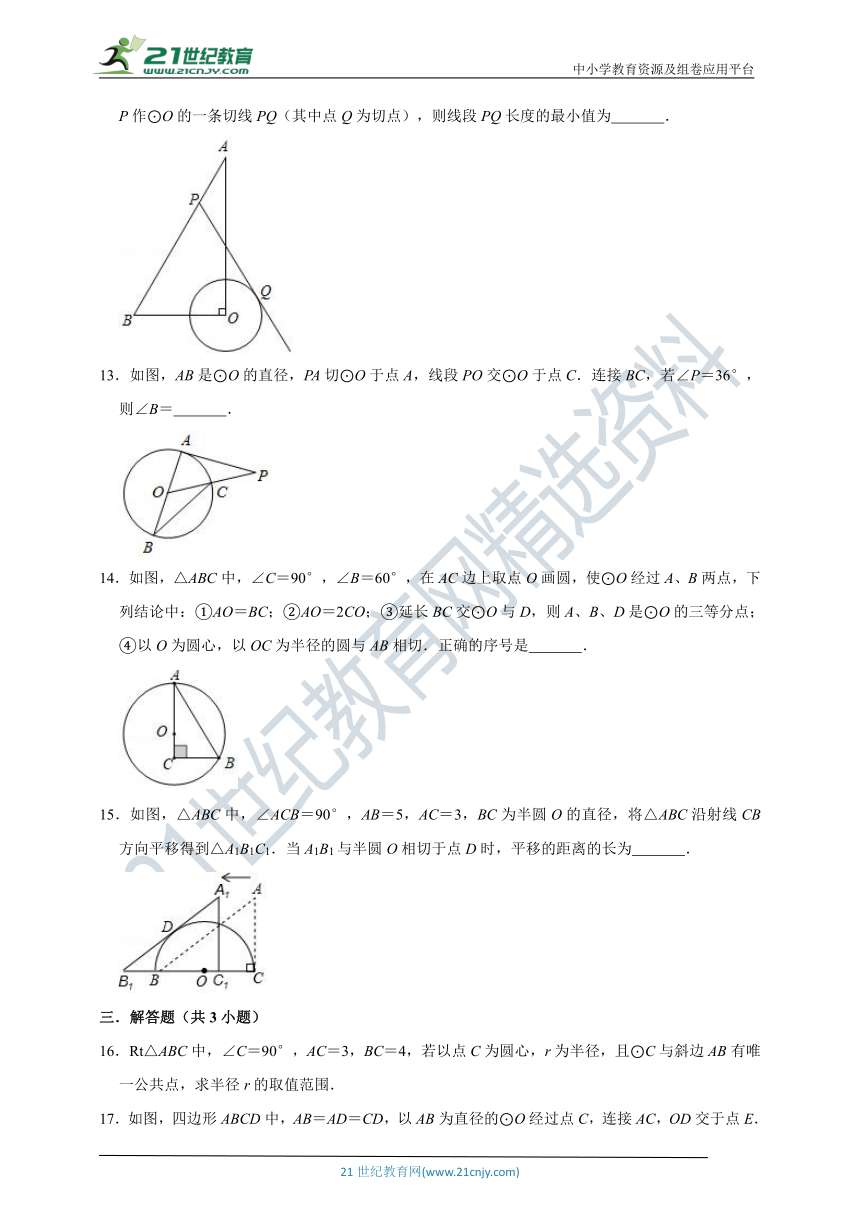
12.如图,在Rt△AOB中,OB=2,∠A=30°,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(其中点Q为切点),则线段PQ长度的最小值为
.
13.如图,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C.连接BC,若∠P=36°,则∠B=
.
14.如图,△ABC中,∠C=90°,∠B=60°,在AC边上取点O画圆,使⊙O经过A、B两点,下列结论中:①AO=BC;②AO=2CO;③延长BC交⊙O与D,则A、B、D是⊙O的三等分点;④以O为圆心,以OC为半径的圆与AB相切.正确的序号是
.
15.如图,△ABC中,∠ACB=90°,AB=5,AC=3,BC为半圆O的直径,将△ABC沿射线CB方向平移得到△A1B1C1.当A1B1与半圆O相切于点D时,平移的距离的长为
.
三.解答题(共3小题)
16.Rt△ABC中,∠C=90°,AC=3,BC=4,若以点C为圆心,r为半径,且⊙C与斜边AB有唯一公共点,求半径r的取值范围.
17.如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.
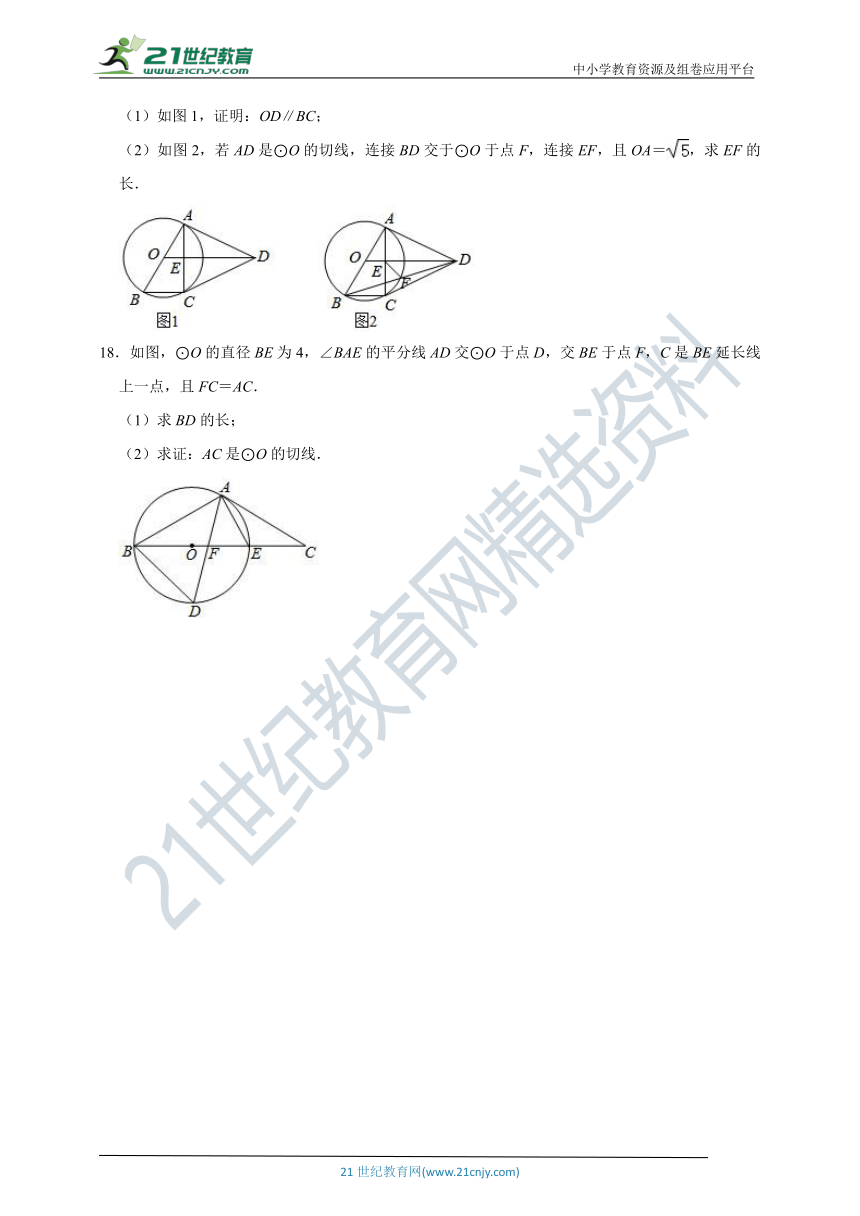
(1)如图1,证明:OD∥BC;
(2)如图2,若AD是⊙O的切线,连接BD交于⊙O于点F,连接EF,且OA=,求EF的长.
18.如图,⊙O的直径BE为4,∠BAE的平分线AD交⊙O于点D,交BE于点F,C是BE延长线上一点,且FC=AC.
(1)求BD的长;
(2)求证:AC是⊙O的切线.
24.2.2
直线和圆的位置关系(1)
参考答案与试题解析
一.选择题(共9小题)
1.平面直角坐标系中,⊙P的圆心坐标为(﹣4,﹣5),半径为5,那么⊙P与y轴的位置关系是( )
A.相交
B.相离
C.相切
D.以上都不是
【分析】由题意可求⊙P到y轴的距离d为4,根据直线与圆的位置关系的判定方法可求解.
【解答】解:∵⊙P的圆心坐标为(﹣4,﹣5),
∴⊙P到y轴的距离d为4
∵d=4<r=5
∴y轴与⊙P相交
故选:A.
【点评】本题考查了直线与圆的位置关系,坐标与图形性质,熟练运用直线与与圆的位置关系的判定方法是解决问题的关键.
2.已知⊙O的半径为7,直线l与⊙O相交,点O到直线l的距离为4,则⊙O上到直线l的距离为3的点共有( )
A.1个
B.2个
C.3个
D.4个
【分析】根据平行线间的距离相等,先过点D作AB⊥OC,即可求得⊙O上到直线l的距离为3的点的个数.
【解答】解:如图,
∵⊙O的半径为7,点O到直线l的距离为4,
∴CE=3,
过点D作AB⊥OC,垂足为D,交⊙O于A、B两点,且DE=3,
∴⊙O上到直线l的距离为3的点为A、B、C,
故选:C.
【点评】本题考查的是直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定.
3.已知线段AB=2,点A,B到直线l的距离分别为方程x2﹣6x+6=0的两根,符合条件的直线l有( )
A.1条
B.2条
C.3条
D.4条
【分析】以A、B为圆心、以两根长为半径作圆,利用直线和两圆的位置关系来进行解答.
【解答】解:解方程x2﹣6x+6=0得x1=3+,x2=3﹣,
①当点A到l的距离>点B到l的距离时,
如图1,分别以A,B为圆心,3+和3﹣为半径画圆,两圆的公切线,即符合条件的直线l;
②当点A到l的距离<点B到l的距离时,
如图2,分别以A,B为圆心,3﹣和3+为半径画圆,两圆的公切线,即符合条件的直线l.
故符合条线的直线l有2条.
故选:B.
【点评】本题考查了直线与圆的位置关系,当圆心到直线的距离d=圆的半径r,直线与圆相切,注意此题两圆恰好内切.
4.如图,以矩形ABCD对角线BD上一点O为圆心作⊙O过A点并与CD切于E点,若CD=3,BC=5,则⊙O的半径为( )
A.
B.3
C.
D.
【分析】作OF⊥AD于F,连接OE,如图,设⊙O的半径为r,利用切线的性质OE⊥CD,利用四边形ABCD为矩形得到OF=DE,DF=OE=r,再证明△DOE∽△DBC,利用相似比得到DE=r,然后在Rt△AOF中利用勾股定理得到(5﹣r)2+(r)2=r2,最后解方程即可.
【解答】解:作OF⊥AD于F,连接OE,如图,设⊙O的半径为r,
∵CD为切线,
∴OE⊥CD,
易得四边形ABCD为矩形,
∴OF=DE,DF=OE=r,
∵OE∥BC,
∴△DOE∽△DBC,
∴=,即=,解得DE=r,
∴OF=r,
在Rt△AOF中,OA=r,AF=5﹣r,
∴(5﹣r)2+(r)2=r2,
整理得9r2﹣250r+625=0,解得r1=25(舍去),r2=,
即⊙O的半径为.
故选:A.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了矩形的性质和相似三角形的判定与性质.
5.如图,AB是⊙O的弦,AC与⊙O相切于点A,连接OA,OB,若∠O=130°,则∠BAC的度数是( )
A.60°
B.65°
C.70°
D.75°
【分析】由“AC与⊙O相切于点A“得出AC⊥OA,根据等边对等角得出∠OAB=∠OBA.求出∠OAC及∠OAB即可解决问题.
【解答】解:∵AC与⊙O相切于点A,
∴AC⊥OA,
∴∠OAC=90°,
∵OA=OB,
∴∠OAB=∠OBA.
∵∠O=130°,
∴∠OAB==25°,
∴∠BAC=∠OAC﹣∠OAB=90°﹣25°=65°.
故选:B.
【点评】本题考查切线的性质,等腰三角形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
6.如图,△ABC内接于圆,∠ACB=90°,过点C的切线交AB的延长线于点P,∠P=28°.则∠CAB=( )
A.62°
B.31°
C.28°
D.56°
【分析】连接OC,如图,根据切线的性质得到∠PCO=90°,则利用互余计算出∠POC=62°,然后根据等腰三角形的性质和三角形外角性质计算∠A的度数.
【解答】解:连接OC,如图,
∵PC为切线,
∴OC⊥PC,
∴∠PCO=90°,
∴∠POC=90°﹣∠P=90°﹣28°=62°,
∵OA=OC,
∴∠A=∠OCA,
而∠POC=∠A+∠OCA,
∴∠A=×62°=31°.
故选:B.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,一般要连接过切点的半径,构造定理图,得出垂直关系.
7.如图,在平面直角坐标系中,过格点A,B,C画圆弧,则点B与下列格点连线所得的直线中,能够与该圆弧相切的格点坐标是( )
A.(5,2)
B.(2,4)
C.(1,4)
D.(6,2)
【分析】根据切线的判定在网格中作图即可得结论.
【解答】解:如图,
过格点A,B,C画圆弧,则点B与下列格点连线所得的直线中,
能够与该圆弧相切的格点坐标是(6,2).
故选:D.
【点评】本题考查了切线的判定,解决本题的关键是掌握切线的判定定理.
8.如图,点D是△ABC中BC边的中点,DE⊥AC于E,以AB为直径的⊙O经过D,连接AD,有下列结论:①AD⊥BC;②∠EDA=∠B;③OA=AC;④DE是⊙O的切线.其中正确的结论是( )
A.①②
B.①②③
C.②③
D.①②③④
【分析】根据直径所对的圆周角是直角,即可判断出选项①正确;由O为AB中点,得到AO为AB的一半,故AO为AC的一半,选项③正确;由OD为三角形ABC的中位线,根据三角形的中位线定理得到OD与AC平行,由AC与DE垂直得到OD与DE垂直,即∠ODE为90°,故DE为圆O的切线,选项④正确.
【解答】解:∵AB是⊙O直径,
∴∠ADB=90°,
∴AD⊥BC,选项①正确;
连接OD,如图,
∵D为BC中点,O为AB中点,
∴DO为△ABC的中位线,
∴OD∥AC,
又DE⊥AC,
∴∠DEA=90°,
∴∠ODE=90°,
∴DE为圆O的切线,选项④正确;
又OB=OD,
∴∠ODB=∠B,
∵AB为圆O的直径,
∴∠ADB=90°,
∵∠EDA+∠ADO=90°,∠BDO+∠ADO=90°,
∴∠EDA=∠BDO,
∴∠EDA=∠B,选项②正确;
由D为BC中点,且AD⊥BC,
∴AD垂直平分BC,
∴AC=AB,又OA=AB,
∴OA=AC,选项③正确;
则正确的结论为①②③④.
故选:D.
【点评】此题考查了相似三角形的判定与性质,切线的判定,及三角形的中位线定理.证明切线时连接OD是解这类题经常连接的辅助线.
9.已知在矩形ABCD中,AB=5,对角线AC=13.⊙C的半径长为12,下列说法正确的是( )
A.⊙C与直线AB相交
B.⊙C与直线AD相切
C.点A在⊙C上
D.点D在⊙C内
【分析】根据点和圆的位置关系及直线和圆的位置关系判断即可.
【解答】解:∵在△ABC中,∠ACB=90°,AC=13,AB=5,
∴BC===12,
∵⊙C的半径长为12,
∴⊙C与直线AB相切,
故A选项不正确,
∵CD=AB=5<12,
∴⊙C与直线AD相交,
故B选项不正确,
∵AC=13>12,
∴点A在⊙C外,
故C选项不正确,
∵CD=5<12,
∴点D在⊙C内,
故D选项正确,
故选:D.
【点评】本题考查了点与圆的位置关系,直线与圆的位置关系,熟练掌握切线的判定及点与圆的位置关系是解题的关键.
二.填空题(共6小题)
10.⊙O的半径为4,圆心O到直线l的距离为2,则直线l与⊙O的位置关系是 相交 .
【分析】根据圆心O到直线l的距离小于半径即可判定直线l与⊙O的位置关系为相交.
【解答】解:∵圆心O到直线l的距离是2,小于⊙O的半径为4,
∴直线l与⊙O相交.
故答案为:相交.
【点评】此题考查的是直线与圆的位置关系,根据圆心到直线的距离d与半径r的大小关系解答.若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
11.直线y=kx+6k交x轴于点A,交y轴于点B,以原点O为圆心,3为半径的⊙O与l相交,则k的取值范围为 ﹣<k< .
【分析】根据题意得到A(﹣6,0),B(0,6k),设⊙O于AB相切于C,连接OC,求得∠OAC=30°,于是得到结论.
【解答】解:∵直线y=kx+6k交x轴于点A,交y轴于点B,
∴A(﹣6,0),B(0,6k),
设⊙O与AB相切于C,
连接OC,
∴OA=6,OC=3,∠ACO=90°,
∴OC=OA,
∴∠OAC=30°,
当⊙O与l相交时,OB=|6k|>2,
∴﹣<k<,
故答案为﹣<k<.
【点评】本题考查了直线与圆的位置关系,一次函数图象与系数的关系,正确的作出图形是解题的关键.
12.如图,在Rt△AOB中,OB=2,∠A=30°,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(其中点Q为切点),则线段PQ长度的最小值为 2 .
【分析】连接OP、OQ,作OP′⊥AB于P′,根据切线的性质得到OQ⊥PQ,根据勾股定理得到PQ=,根据垂线段最短得到当OP⊥AB时,OP最小,根据直角三角形的性质、勾股定理计算即可.
【解答】解:连接OP、OQ,作OP′⊥AB于P′,
∵PQ是⊙O的切线,
∴OQ⊥PQ,
∴PQ==,
当OP最小时,线段PQ的长度最小,
当OP⊥AB时,OP最小,
在Rt△AOB中,∠A=30°,
∴OA==6,
在Rt△AOP′中,∠A=30°,
∴OP′=OA=3,
∴线段PQ长度的最小值==2,
故答案为:2.
【点评】本题考查的是切线的性质、勾股定理、直角三角形的性质,掌握圆的切线垂直于经过切点的半径是解题的关键.
13.如图,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C.连接BC,若∠P=36°,则∠B= 27° .
【分析】直接利用切线的性质得出∠OAP=90°,再利用三角形内角和定理得出∠AOP=54°,结合圆周角定理得出答案.
【解答】解:∵PA切⊙O于点A,
∴∠OAP=90°,
∵∠P=36°,
∴∠AOP=54°,
∵=,
∴∠B=∠AOP=27°.
故答案为:27°.
【点评】此题主要考查了切线的性质以及圆周角定理,正确得出∠AOP的度数是解题关键.
14.如图,△ABC中,∠C=90°,∠B=60°,在AC边上取点O画圆,使⊙O经过A、B两点,下列结论中:①AO=BC;②AO=2CO;③延长BC交⊙O与D,则A、B、D是⊙O的三等分点;④以O为圆心,以OC为半径的圆与AB相切.正确的序号是 ②③④ .
【分析】连接OB,可得∠ABO=30°,则∠OBC=30°,根据三角函数cos∠OBC=,则BC=OB,根据直角三角形的性质得OC=OB=OA,根据垂径定理得直线AC是弦BD的垂直平分线,则点A、B、D将⊙O的三等分,因为点O在∠ABC的角平分线上,所以点O到直线AB的距离等于OC的长.
【解答】解:连接OB,
∵OA=OB,
∴∠A=∠ABO,
∵∠C=90°,∠B=60°,
∴∠A=30°,
∴∠OBC=30°,
∵cos∠OBC=,
∴BC=,
即BC=,
故①错误,
∵∠OBC=30°,
∴OC=OB=OA,
即OA=2OC,
故②正确;
延长BC交⊙O于D,
∵AC⊥BD,
∴AD=AB,
∴△ABD为等边三角形,
∴==,
∴点A、B、D将⊙O的三等分;
故③正确;
∵∠ABO=∠OBC=30°,
∴点O在∠ABC的角平分线上,
∴点O到直线AB的距离等于OC的长,
即以O为圆心,以OC为半径的圆与AB相切.
故④正确.
故答案为:②③④.
【点评】本题考查了直角三角形的性质、勾股定理和垂径定理,等边三角形的判定与性质,正确作出辅助线是解题的关键.
15.如图,△ABC中,∠ACB=90°,AB=5,AC=3,BC为半圆O的直径,将△ABC沿射线CB方向平移得到△A1B1C1.当A1B1与半圆O相切于点D时,平移的距离的长为 .
【分析】连结OG,如图,根据勾股定理得到BC==4,根据平移的性质得到CC1=BB1,A1C1=AC=3,A1B1=AB=5,∠A1C1B1=∠ACB=90°,根据切线的性质得到OD⊥A1B1,根据相似三角形的性质即可得到结论.
【解答】解:连结OG,如图,
∵∠BAC=90°,AB=5,AC=3,
∴BC==4,
∵Rt△ABC沿射线CB方向平移,当A1B1与半圆O相切于点D,得△A1B1C1,
∴CC1=BB1,A1C1=AC=3,A1B1=AB=5,∠A1C1B1=∠ACB=90°,
∵A1B1与半圆O相切于点D,
∴OD⊥A1B1,
∵BC=4,线段BC为半圆O的直径,
∴OB=OC=2,
∵∠GEO=∠DEF,
∴Rt△B1OD∽Rt△B1A1C1,
∴=,即=,解得OB1=,
∴BB1=OB1﹣OB=﹣2=;
故答案为:.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了平移的性质、勾股定理和相似三角形的判定与性质.
三.解答题(共3小题)
16.Rt△ABC中,∠C=90°,AC=3,BC=4,若以点C为圆心,r为半径,且⊙C与斜边AB有唯一公共点,求半径r的取值范围.
【分析】此题注意两种情况:
(1)圆与AB相切时;
(2)点A在圆内部,点B在圆上或圆外时.
根据勾股定理以及直角三角形的面积计算出其斜边上的高,再根据位置关系与数量之间的联系进行求解.
【解答】解:如图,∵BC>AC,
∴以C为圆心,r为半径所作的圆与斜边AB只有一个公共点.
根据勾股定理求得AB=5.
分两种情况:
(1)圆与AB相切时,即r=CD=3×4÷5=2.4;
(2)点A在圆内部,点B在圆上或圆外时,此时AC<r≤BC,即3<r≤4.
∴3<r≤4或r=2.4.
【点评】此题考查了直线与圆的位置关系,此题注意考虑两种情况,只需保证圆和斜边只有一个公共点即可.
17.如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.
(1)如图1,证明:OD∥BC;
(2)如图2,若AD是⊙O的切线,连接BD交于⊙O于点F,连接EF,且OA=,求EF的长.
【分析】(1)连接OC,证明△OAD≌△OCD(SSS)得∠ADO=∠CDO,由AD=CD知DE⊥AC,再由AB为直径知BC⊥AC,从而得OD∥BC;
(2)连接AF,过F作FM⊥EF交OD于M,推出△ABD为等腰直角三角形,求得∠AFB=90°,∠DAF=∠45°,根据全等三角形的性质即可得到结论.
【解答】解:(1)连接OC,
在△OAD和△OCD中,
,
∴△OAD≌△OCD(SSS),
∴∠ADO=∠CDO,
又AD=CD,
∴DE⊥AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
即BC⊥AC,
∴OD∥BC;
(2)连接AF,过F作FM⊥EF交OD于M,
∵AB=AD,AD是圆的切线,
∴△ABD为等腰直角三角形,
∵AB为直径,
∴∠AFB=90°,∠DAF=45°,
∵∠AED=∠AFD=90°,
∴∠DAF=∠ADF=45°,∠EAF=∠FDM,
∴AF=DF,
∵∠EFM=∠AFD=90°,
∴∠AFE=∠DFM,
∴△AEF≌△DMF(ASA),
∴AE=DM,
∵,OA=,
∴OD==5,
∴AE=DM==2,DE=4,
∴EM=4﹣2=2,
∴EF=.
【点评】本题考查了切线的性质,全等三角形的判定和性质,等腰直角三角形的判定和性质,正确的作出辅助线是解题的关键.
18.如图,⊙O的直径BE为4,∠BAE的平分线AD交⊙O于点D,交BE于点F,C是BE延长线上一点,且FC=AC.
(1)求BD的长;
(2)求证:AC是⊙O的切线.
【分析】(1)连接OD.证得∠BOD=2∠BAD=90°,由勾股定理可得出答案;
(2)连接OA.证得∠DFO+∠ODF=∠CAF+∠OAF=90°.则OA⊥AC于A,可得出结论.
【解答】(1)解:如图1,连接OD.
∵BE为⊙O的直径,
∴∠BAE=90°.
∵AD平分∠BAE,∠BAD=∠EAD=45°.
∴∠BOD=2∠BAD=90°.
∴Rt△BOD中,.
(2)证明:如图,连接OA.
∵AC=FC,
∴∠FAC=∠CFA.
∵∠DFO=∠CFA,
∴∠DFO=∠FAC.
∵OA=OD,
∴∠OAF=∠ODF.
由(1)知∠BOD=90°,
∴∠DFO+∠ODF=∠CAF+∠OAF=90°.
∴OA⊥AC于A,
∴AC是⊙O的切线.
【点评】本题考查了切线的判定,等腰三角形的性质,勾股定理,圆周角定理,熟练掌握切线的判定是解题的关键.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/9
9:05:56;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
24.2.2
直线和圆的位置关系(1)
一.选择题(共9小题)
1.平面直角坐标系中,⊙P的圆心坐标为(﹣4,﹣5),半径为5,那么⊙P与y轴的位置关系是( )
A.相交
B.相离
C.相切
D.以上都不是
2.已知⊙O的半径为7,直线l与⊙O相交,点O到直线l的距离为4,则⊙O上到直线l的距离为3的点共有( )
A.1个
B.2个
C.3个
D.4个
3.已知线段AB=2,点A,B到直线l的距离分别为方程x2﹣6x+6=0的两根,符合条件的直线l有( )
A.1条
B.2条
C.3条
D.4条
4.如图,以矩形ABCD对角线BD上一点O为圆心作⊙O过A点并与CD切于E点,若CD=3,BC=5,则⊙O的半径为( )
A.
B.3
C.
D.
5.如图,AB是⊙O的弦,AC与⊙O相切于点A,连接OA,OB,若∠O=130°,则∠BAC的度数是( )
A.60°
B.65°
C.70°
D.75°
6.如图,△ABC内接于圆,∠ACB=90°,过点C的切线交AB的延长线于点P,∠P=28°.则∠CAB=( )
A.62°
B.31°
C.28°
D.56°
7.如图,在平面直角坐标系中,过格点A,B,C画圆弧,则点B与下列格点连线所得的直线中,能够与该圆弧相切的格点坐标是( )
A.(5,2)
B.(2,4)
C.(1,4)
D.(6,2)
8.如图,点D是△ABC中BC边的中点,DE⊥AC于E,以AB为直径的⊙O经过D,连接AD,有下列结论:①AD⊥BC;②∠EDA=∠B;③OA=AC;④DE是⊙O的切线.其中正确的结论是( )
A.①②
B.①②③
C.②③
D.①②③④
9.已知在矩形ABCD中,AB=5,对角线AC=13.⊙C的半径长为12,下列说法正确的是( )
A.⊙C与直线AB相交
B.⊙C与直线AD相切
C.点A在⊙C上
D.点D在⊙C内
二.填空题(共6小题)
10.⊙O的半径为4,圆心O到直线l的距离为2,则直线l与⊙O的位置关系是
.
11.直线y=kx+6k交x轴于点A,交y轴于点B,以原点O为圆心,3为半径的⊙O与l相交,则k的取值范围为
.
12.如图,在Rt△AOB中,OB=2,∠A=30°,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(其中点Q为切点),则线段PQ长度的最小值为
.
13.如图,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C.连接BC,若∠P=36°,则∠B=
.
14.如图,△ABC中,∠C=90°,∠B=60°,在AC边上取点O画圆,使⊙O经过A、B两点,下列结论中:①AO=BC;②AO=2CO;③延长BC交⊙O与D,则A、B、D是⊙O的三等分点;④以O为圆心,以OC为半径的圆与AB相切.正确的序号是
.
15.如图,△ABC中,∠ACB=90°,AB=5,AC=3,BC为半圆O的直径,将△ABC沿射线CB方向平移得到△A1B1C1.当A1B1与半圆O相切于点D时,平移的距离的长为
.
三.解答题(共3小题)
16.Rt△ABC中,∠C=90°,AC=3,BC=4,若以点C为圆心,r为半径,且⊙C与斜边AB有唯一公共点,求半径r的取值范围.
17.如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.
(1)如图1,证明:OD∥BC;
(2)如图2,若AD是⊙O的切线,连接BD交于⊙O于点F,连接EF,且OA=,求EF的长.
18.如图,⊙O的直径BE为4,∠BAE的平分线AD交⊙O于点D,交BE于点F,C是BE延长线上一点,且FC=AC.
(1)求BD的长;
(2)求证:AC是⊙O的切线.
24.2.2
直线和圆的位置关系(1)
参考答案与试题解析
一.选择题(共9小题)
1.平面直角坐标系中,⊙P的圆心坐标为(﹣4,﹣5),半径为5,那么⊙P与y轴的位置关系是( )
A.相交
B.相离
C.相切
D.以上都不是
【分析】由题意可求⊙P到y轴的距离d为4,根据直线与圆的位置关系的判定方法可求解.
【解答】解:∵⊙P的圆心坐标为(﹣4,﹣5),
∴⊙P到y轴的距离d为4
∵d=4<r=5
∴y轴与⊙P相交
故选:A.
【点评】本题考查了直线与圆的位置关系,坐标与图形性质,熟练运用直线与与圆的位置关系的判定方法是解决问题的关键.
2.已知⊙O的半径为7,直线l与⊙O相交,点O到直线l的距离为4,则⊙O上到直线l的距离为3的点共有( )
A.1个
B.2个
C.3个
D.4个
【分析】根据平行线间的距离相等,先过点D作AB⊥OC,即可求得⊙O上到直线l的距离为3的点的个数.
【解答】解:如图,
∵⊙O的半径为7,点O到直线l的距离为4,
∴CE=3,
过点D作AB⊥OC,垂足为D,交⊙O于A、B两点,且DE=3,
∴⊙O上到直线l的距离为3的点为A、B、C,
故选:C.
【点评】本题考查的是直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定.
3.已知线段AB=2,点A,B到直线l的距离分别为方程x2﹣6x+6=0的两根,符合条件的直线l有( )
A.1条
B.2条
C.3条
D.4条
【分析】以A、B为圆心、以两根长为半径作圆,利用直线和两圆的位置关系来进行解答.
【解答】解:解方程x2﹣6x+6=0得x1=3+,x2=3﹣,
①当点A到l的距离>点B到l的距离时,
如图1,分别以A,B为圆心,3+和3﹣为半径画圆,两圆的公切线,即符合条件的直线l;
②当点A到l的距离<点B到l的距离时,
如图2,分别以A,B为圆心,3﹣和3+为半径画圆,两圆的公切线,即符合条件的直线l.
故符合条线的直线l有2条.
故选:B.
【点评】本题考查了直线与圆的位置关系,当圆心到直线的距离d=圆的半径r,直线与圆相切,注意此题两圆恰好内切.
4.如图,以矩形ABCD对角线BD上一点O为圆心作⊙O过A点并与CD切于E点,若CD=3,BC=5,则⊙O的半径为( )
A.
B.3
C.
D.
【分析】作OF⊥AD于F,连接OE,如图,设⊙O的半径为r,利用切线的性质OE⊥CD,利用四边形ABCD为矩形得到OF=DE,DF=OE=r,再证明△DOE∽△DBC,利用相似比得到DE=r,然后在Rt△AOF中利用勾股定理得到(5﹣r)2+(r)2=r2,最后解方程即可.
【解答】解:作OF⊥AD于F,连接OE,如图,设⊙O的半径为r,
∵CD为切线,
∴OE⊥CD,
易得四边形ABCD为矩形,
∴OF=DE,DF=OE=r,
∵OE∥BC,
∴△DOE∽△DBC,
∴=,即=,解得DE=r,
∴OF=r,
在Rt△AOF中,OA=r,AF=5﹣r,
∴(5﹣r)2+(r)2=r2,
整理得9r2﹣250r+625=0,解得r1=25(舍去),r2=,
即⊙O的半径为.
故选:A.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了矩形的性质和相似三角形的判定与性质.
5.如图,AB是⊙O的弦,AC与⊙O相切于点A,连接OA,OB,若∠O=130°,则∠BAC的度数是( )
A.60°
B.65°
C.70°
D.75°
【分析】由“AC与⊙O相切于点A“得出AC⊥OA,根据等边对等角得出∠OAB=∠OBA.求出∠OAC及∠OAB即可解决问题.
【解答】解:∵AC与⊙O相切于点A,
∴AC⊥OA,
∴∠OAC=90°,
∵OA=OB,
∴∠OAB=∠OBA.
∵∠O=130°,
∴∠OAB==25°,
∴∠BAC=∠OAC﹣∠OAB=90°﹣25°=65°.
故选:B.
【点评】本题考查切线的性质,等腰三角形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
6.如图,△ABC内接于圆,∠ACB=90°,过点C的切线交AB的延长线于点P,∠P=28°.则∠CAB=( )
A.62°
B.31°
C.28°
D.56°
【分析】连接OC,如图,根据切线的性质得到∠PCO=90°,则利用互余计算出∠POC=62°,然后根据等腰三角形的性质和三角形外角性质计算∠A的度数.
【解答】解:连接OC,如图,
∵PC为切线,
∴OC⊥PC,
∴∠PCO=90°,
∴∠POC=90°﹣∠P=90°﹣28°=62°,
∵OA=OC,
∴∠A=∠OCA,
而∠POC=∠A+∠OCA,
∴∠A=×62°=31°.
故选:B.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,一般要连接过切点的半径,构造定理图,得出垂直关系.
7.如图,在平面直角坐标系中,过格点A,B,C画圆弧,则点B与下列格点连线所得的直线中,能够与该圆弧相切的格点坐标是( )
A.(5,2)
B.(2,4)
C.(1,4)
D.(6,2)
【分析】根据切线的判定在网格中作图即可得结论.
【解答】解:如图,
过格点A,B,C画圆弧,则点B与下列格点连线所得的直线中,
能够与该圆弧相切的格点坐标是(6,2).
故选:D.
【点评】本题考查了切线的判定,解决本题的关键是掌握切线的判定定理.
8.如图,点D是△ABC中BC边的中点,DE⊥AC于E,以AB为直径的⊙O经过D,连接AD,有下列结论:①AD⊥BC;②∠EDA=∠B;③OA=AC;④DE是⊙O的切线.其中正确的结论是( )
A.①②
B.①②③
C.②③
D.①②③④
【分析】根据直径所对的圆周角是直角,即可判断出选项①正确;由O为AB中点,得到AO为AB的一半,故AO为AC的一半,选项③正确;由OD为三角形ABC的中位线,根据三角形的中位线定理得到OD与AC平行,由AC与DE垂直得到OD与DE垂直,即∠ODE为90°,故DE为圆O的切线,选项④正确.
【解答】解:∵AB是⊙O直径,
∴∠ADB=90°,
∴AD⊥BC,选项①正确;
连接OD,如图,
∵D为BC中点,O为AB中点,
∴DO为△ABC的中位线,
∴OD∥AC,
又DE⊥AC,
∴∠DEA=90°,
∴∠ODE=90°,
∴DE为圆O的切线,选项④正确;
又OB=OD,
∴∠ODB=∠B,
∵AB为圆O的直径,
∴∠ADB=90°,
∵∠EDA+∠ADO=90°,∠BDO+∠ADO=90°,
∴∠EDA=∠BDO,
∴∠EDA=∠B,选项②正确;
由D为BC中点,且AD⊥BC,
∴AD垂直平分BC,
∴AC=AB,又OA=AB,
∴OA=AC,选项③正确;
则正确的结论为①②③④.
故选:D.
【点评】此题考查了相似三角形的判定与性质,切线的判定,及三角形的中位线定理.证明切线时连接OD是解这类题经常连接的辅助线.
9.已知在矩形ABCD中,AB=5,对角线AC=13.⊙C的半径长为12,下列说法正确的是( )
A.⊙C与直线AB相交
B.⊙C与直线AD相切
C.点A在⊙C上
D.点D在⊙C内
【分析】根据点和圆的位置关系及直线和圆的位置关系判断即可.
【解答】解:∵在△ABC中,∠ACB=90°,AC=13,AB=5,
∴BC===12,
∵⊙C的半径长为12,
∴⊙C与直线AB相切,
故A选项不正确,
∵CD=AB=5<12,
∴⊙C与直线AD相交,
故B选项不正确,
∵AC=13>12,
∴点A在⊙C外,
故C选项不正确,
∵CD=5<12,
∴点D在⊙C内,
故D选项正确,
故选:D.
【点评】本题考查了点与圆的位置关系,直线与圆的位置关系,熟练掌握切线的判定及点与圆的位置关系是解题的关键.
二.填空题(共6小题)
10.⊙O的半径为4,圆心O到直线l的距离为2,则直线l与⊙O的位置关系是 相交 .
【分析】根据圆心O到直线l的距离小于半径即可判定直线l与⊙O的位置关系为相交.
【解答】解:∵圆心O到直线l的距离是2,小于⊙O的半径为4,
∴直线l与⊙O相交.
故答案为:相交.
【点评】此题考查的是直线与圆的位置关系,根据圆心到直线的距离d与半径r的大小关系解答.若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
11.直线y=kx+6k交x轴于点A,交y轴于点B,以原点O为圆心,3为半径的⊙O与l相交,则k的取值范围为 ﹣<k< .
【分析】根据题意得到A(﹣6,0),B(0,6k),设⊙O于AB相切于C,连接OC,求得∠OAC=30°,于是得到结论.
【解答】解:∵直线y=kx+6k交x轴于点A,交y轴于点B,
∴A(﹣6,0),B(0,6k),
设⊙O与AB相切于C,
连接OC,
∴OA=6,OC=3,∠ACO=90°,
∴OC=OA,
∴∠OAC=30°,
当⊙O与l相交时,OB=|6k|>2,
∴﹣<k<,
故答案为﹣<k<.
【点评】本题考查了直线与圆的位置关系,一次函数图象与系数的关系,正确的作出图形是解题的关键.
12.如图,在Rt△AOB中,OB=2,∠A=30°,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(其中点Q为切点),则线段PQ长度的最小值为 2 .
【分析】连接OP、OQ,作OP′⊥AB于P′,根据切线的性质得到OQ⊥PQ,根据勾股定理得到PQ=,根据垂线段最短得到当OP⊥AB时,OP最小,根据直角三角形的性质、勾股定理计算即可.
【解答】解:连接OP、OQ,作OP′⊥AB于P′,
∵PQ是⊙O的切线,
∴OQ⊥PQ,
∴PQ==,
当OP最小时,线段PQ的长度最小,
当OP⊥AB时,OP最小,
在Rt△AOB中,∠A=30°,
∴OA==6,
在Rt△AOP′中,∠A=30°,
∴OP′=OA=3,
∴线段PQ长度的最小值==2,
故答案为:2.
【点评】本题考查的是切线的性质、勾股定理、直角三角形的性质,掌握圆的切线垂直于经过切点的半径是解题的关键.
13.如图,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C.连接BC,若∠P=36°,则∠B= 27° .
【分析】直接利用切线的性质得出∠OAP=90°,再利用三角形内角和定理得出∠AOP=54°,结合圆周角定理得出答案.
【解答】解:∵PA切⊙O于点A,
∴∠OAP=90°,
∵∠P=36°,
∴∠AOP=54°,
∵=,
∴∠B=∠AOP=27°.
故答案为:27°.
【点评】此题主要考查了切线的性质以及圆周角定理,正确得出∠AOP的度数是解题关键.
14.如图,△ABC中,∠C=90°,∠B=60°,在AC边上取点O画圆,使⊙O经过A、B两点,下列结论中:①AO=BC;②AO=2CO;③延长BC交⊙O与D,则A、B、D是⊙O的三等分点;④以O为圆心,以OC为半径的圆与AB相切.正确的序号是 ②③④ .
【分析】连接OB,可得∠ABO=30°,则∠OBC=30°,根据三角函数cos∠OBC=,则BC=OB,根据直角三角形的性质得OC=OB=OA,根据垂径定理得直线AC是弦BD的垂直平分线,则点A、B、D将⊙O的三等分,因为点O在∠ABC的角平分线上,所以点O到直线AB的距离等于OC的长.
【解答】解:连接OB,
∵OA=OB,
∴∠A=∠ABO,
∵∠C=90°,∠B=60°,
∴∠A=30°,
∴∠OBC=30°,
∵cos∠OBC=,
∴BC=,
即BC=,
故①错误,
∵∠OBC=30°,
∴OC=OB=OA,
即OA=2OC,
故②正确;
延长BC交⊙O于D,
∵AC⊥BD,
∴AD=AB,
∴△ABD为等边三角形,
∴==,
∴点A、B、D将⊙O的三等分;
故③正确;
∵∠ABO=∠OBC=30°,
∴点O在∠ABC的角平分线上,
∴点O到直线AB的距离等于OC的长,
即以O为圆心,以OC为半径的圆与AB相切.
故④正确.
故答案为:②③④.
【点评】本题考查了直角三角形的性质、勾股定理和垂径定理,等边三角形的判定与性质,正确作出辅助线是解题的关键.
15.如图,△ABC中,∠ACB=90°,AB=5,AC=3,BC为半圆O的直径,将△ABC沿射线CB方向平移得到△A1B1C1.当A1B1与半圆O相切于点D时,平移的距离的长为 .
【分析】连结OG,如图,根据勾股定理得到BC==4,根据平移的性质得到CC1=BB1,A1C1=AC=3,A1B1=AB=5,∠A1C1B1=∠ACB=90°,根据切线的性质得到OD⊥A1B1,根据相似三角形的性质即可得到结论.
【解答】解:连结OG,如图,
∵∠BAC=90°,AB=5,AC=3,
∴BC==4,
∵Rt△ABC沿射线CB方向平移,当A1B1与半圆O相切于点D,得△A1B1C1,
∴CC1=BB1,A1C1=AC=3,A1B1=AB=5,∠A1C1B1=∠ACB=90°,
∵A1B1与半圆O相切于点D,
∴OD⊥A1B1,
∵BC=4,线段BC为半圆O的直径,
∴OB=OC=2,
∵∠GEO=∠DEF,
∴Rt△B1OD∽Rt△B1A1C1,
∴=,即=,解得OB1=,
∴BB1=OB1﹣OB=﹣2=;
故答案为:.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了平移的性质、勾股定理和相似三角形的判定与性质.
三.解答题(共3小题)
16.Rt△ABC中,∠C=90°,AC=3,BC=4,若以点C为圆心,r为半径,且⊙C与斜边AB有唯一公共点,求半径r的取值范围.
【分析】此题注意两种情况:
(1)圆与AB相切时;
(2)点A在圆内部,点B在圆上或圆外时.
根据勾股定理以及直角三角形的面积计算出其斜边上的高,再根据位置关系与数量之间的联系进行求解.
【解答】解:如图,∵BC>AC,
∴以C为圆心,r为半径所作的圆与斜边AB只有一个公共点.
根据勾股定理求得AB=5.
分两种情况:
(1)圆与AB相切时,即r=CD=3×4÷5=2.4;
(2)点A在圆内部,点B在圆上或圆外时,此时AC<r≤BC,即3<r≤4.
∴3<r≤4或r=2.4.
【点评】此题考查了直线与圆的位置关系,此题注意考虑两种情况,只需保证圆和斜边只有一个公共点即可.
17.如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.
(1)如图1,证明:OD∥BC;
(2)如图2,若AD是⊙O的切线,连接BD交于⊙O于点F,连接EF,且OA=,求EF的长.
【分析】(1)连接OC,证明△OAD≌△OCD(SSS)得∠ADO=∠CDO,由AD=CD知DE⊥AC,再由AB为直径知BC⊥AC,从而得OD∥BC;
(2)连接AF,过F作FM⊥EF交OD于M,推出△ABD为等腰直角三角形,求得∠AFB=90°,∠DAF=∠45°,根据全等三角形的性质即可得到结论.
【解答】解:(1)连接OC,
在△OAD和△OCD中,
,
∴△OAD≌△OCD(SSS),
∴∠ADO=∠CDO,
又AD=CD,
∴DE⊥AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
即BC⊥AC,
∴OD∥BC;
(2)连接AF,过F作FM⊥EF交OD于M,
∵AB=AD,AD是圆的切线,
∴△ABD为等腰直角三角形,
∵AB为直径,
∴∠AFB=90°,∠DAF=45°,
∵∠AED=∠AFD=90°,
∴∠DAF=∠ADF=45°,∠EAF=∠FDM,
∴AF=DF,
∵∠EFM=∠AFD=90°,
∴∠AFE=∠DFM,
∴△AEF≌△DMF(ASA),
∴AE=DM,
∵,OA=,
∴OD==5,
∴AE=DM==2,DE=4,
∴EM=4﹣2=2,
∴EF=.
【点评】本题考查了切线的性质,全等三角形的判定和性质,等腰直角三角形的判定和性质,正确的作出辅助线是解题的关键.
18.如图,⊙O的直径BE为4,∠BAE的平分线AD交⊙O于点D,交BE于点F,C是BE延长线上一点,且FC=AC.
(1)求BD的长;
(2)求证:AC是⊙O的切线.
【分析】(1)连接OD.证得∠BOD=2∠BAD=90°,由勾股定理可得出答案;
(2)连接OA.证得∠DFO+∠ODF=∠CAF+∠OAF=90°.则OA⊥AC于A,可得出结论.
【解答】(1)解:如图1,连接OD.
∵BE为⊙O的直径,
∴∠BAE=90°.
∵AD平分∠BAE,∠BAD=∠EAD=45°.
∴∠BOD=2∠BAD=90°.
∴Rt△BOD中,.
(2)证明:如图,连接OA.
∵AC=FC,
∴∠FAC=∠CFA.
∵∠DFO=∠CFA,
∴∠DFO=∠FAC.
∵OA=OD,
∴∠OAF=∠ODF.
由(1)知∠BOD=90°,
∴∠DFO+∠ODF=∠CAF+∠OAF=90°.
∴OA⊥AC于A,
∴AC是⊙O的切线.
【点评】本题考查了切线的判定,等腰三角形的性质,勾股定理,圆周角定理,熟练掌握切线的判定是解题的关键.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/9
9:05:56;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
同课章节目录
