24.3 正多边形和圆同步练习(含解析)
文档属性
| 名称 | 24.3 正多边形和圆同步练习(含解析) |

|
|
| 格式 | rar | ||
| 文件大小 | 202.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
24.3
正多边形和圆
一.选择题(共3小题)
1.下列说法中正确的是( )
A.直角三角形只有一条高
B.三角形任意两个内角的和大于第3个内角
C.在同圆中任意两条直径都互相平分
D.如果一个多边形的各边都相等,那么它是正多边形
2.半径为R的圆内接正三角形、正方形、正六边形的边心距分别为a,b,c,则a,b,c的大小关系是( )
A.a<b<c
B.b<a<c
C.a<c<b
D.c<b<a
3.若正多边形的中心角为72°,则该正多边形的边数为( )
A.8
B.7
C.6
D.5
二.填空题(共2小题)
4.如图,在同一平面内,将边长相等的正方形、正五边形的一边重合,那么∠1=
°.
5.如图,以AB为边,在AB的同侧分别作正五边形ABCDE和等边△ABF,连接FE,FC,则∠EFA的度数是
.
三.解答题(共1小题)
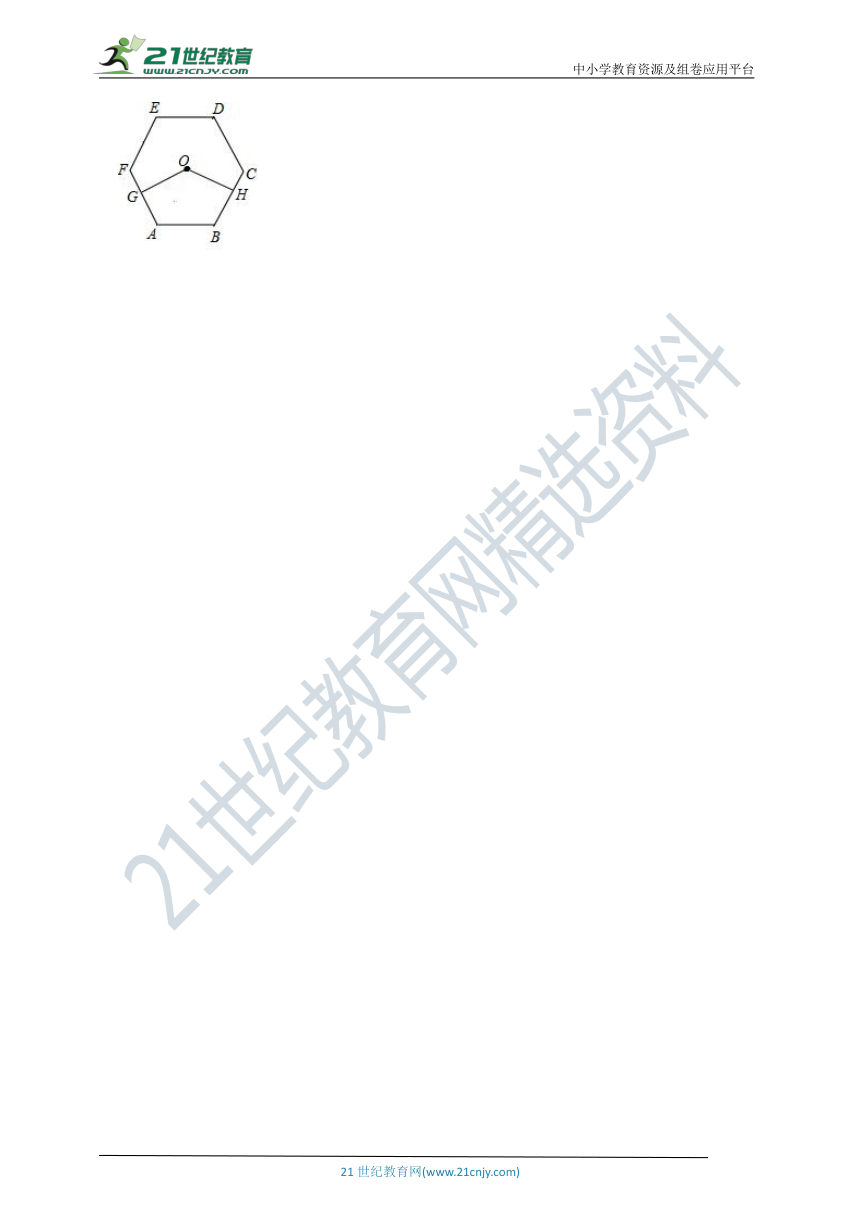
6.如图,已知点O是正六边形ABCDEF的对称中心,G,H分别是AF,BC上的点,且AG=BH.
(1)求∠FAB的度数;
(2)求证:OG=OH.
24.3
正多边形和圆
参考答案与试题解析
一.选择题(共3小题)
1.下列说法中正确的是( )
A.直角三角形只有一条高
B.三角形任意两个内角的和大于第3个内角
C.在同圆中任意两条直径都互相平分
D.如果一个多边形的各边都相等,那么它是正多边形
【分析】利用直角三角形的性质、三角形的内角、圆的性质及正多边形的定义分别判断后即可确定正确的选项.
【解答】解:A、直角三角形有3条高,故原命题错误,不符合题意;
B、钝角三角形的两个较小的锐角的和小于最大的钝角,故原命题错误,不符合题意;
C、在同圆中任意两条直径都互相平分,正确,符合题意;
D、如果一个多边形的各角相等,各边都相等,那么它是正多边形,故原命题错误,不符合题意;
故选:C.
【点评】本题考查了正多边形和圆的知识,解题的关键是了解直角三角形的性质、三角形的内角、圆的性质及正多边形的定义等知识,难度不大.
2.半径为R的圆内接正三角形、正方形、正六边形的边心距分别为a,b,c,则a,b,c的大小关系是( )
A.a<b<c
B.b<a<c
C.a<c<b
D.c<b<a
【分析】根据三角函数即可求解.
【解答】解:设圆的半径为R,
则正三角形的边心距为a=R×cos60°=R.
四边形的边心距为b=R×cos45°=R,
正六边形的边心距为c=R×cos30°=R.
∵RRR,
∴a<b<c,
故选:A.
【点评】此题主要考查了正多边形和圆的性质,解决本题的关键是构造直角三角形,得到用半径表示的边心距;注意:正多边形的计算一般要转化为解直角三角形的问题来解决.
3.若正多边形的中心角为72°,则该正多边形的边数为( )
A.8
B.7
C.6
D.5
【分析】根据正多边形的中心角=,求出n即可.
【解答】解:由题意,=72°,
∴n=5,
故选:D.
【点评】本题考查正多边形的中心角知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
二.填空题(共2小题)
4.如图,在同一平面内,将边长相等的正方形、正五边形的一边重合,那么∠1= 18 °.
【分析】∠1的度数是正五边形的内角与正方形的内角的度数的差,根据多边形的内角和定理求得角的度数即可得出结果.
【解答】解:∵正五边形的内角的度数是
×(5﹣2)×180°=108°,
又∵正方形的内角是90°,
∴∠1=108°﹣90°=18°;
故答案为:18.
【点评】本题考查了正多边形和圆,多边形的内角和定理、正方形的性质,求得正五边形的内角的度数是关键.
5.如图,以AB为边,在AB的同侧分别作正五边形ABCDE和等边△ABF,连接FE,FC,则∠EFA的度数是 66° .
【分析】根据正五边形和等边三角形的性质得到∠EAF=108°﹣60°=48°,根据等腰三角形的性质即可得到结论.
【解答】解:∵正五边形ABCDE,
∴∠EAB==108°,
∵△ABF是等边三角形,
∴∠FAB=60°,
∴∠EAF=108°﹣60°=48°,
∵AE=AF,
∴∠AEF=∠AFE=(180°﹣48°)=66°,
故答案为:66°.
【点评】本题考查了正多边形与圆,正五边形和等边三角形的性质,等腰三角形的性质,正确的识别图形是解题的关键.
三.解答题(共1小题)
6.如图,已知点O是正六边形ABCDEF的对称中心,G,H分别是AF,BC上的点,且AG=BH.
(1)求∠FAB的度数;
(2)求证:OG=OH.
【分析】(1)根据多边形的内角和定理、正多边形的性质计算;
(2)证明△AOG≌△BOH,根据全等三角形的性质证明结论.
【解答】(1)解:∵六边形ABCDEF是正六边形,
∴∠FAB==120°;
(2)证明:连接OA、OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵∠FAB=∠CBA,
∴∠OAG=∠OBH,
在△AOG和△BOH中,
,
∴△AOG≌△BOH(SAS)
∴OG=OH.
【点评】本题考查的是正多边形和圆,掌握正多边形的内角的计算公式、全等三角形的判定定理和性质定理是解题的关键.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/9
9:10:32;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
24.3
正多边形和圆
一.选择题(共3小题)
1.下列说法中正确的是( )
A.直角三角形只有一条高
B.三角形任意两个内角的和大于第3个内角
C.在同圆中任意两条直径都互相平分
D.如果一个多边形的各边都相等,那么它是正多边形
2.半径为R的圆内接正三角形、正方形、正六边形的边心距分别为a,b,c,则a,b,c的大小关系是( )
A.a<b<c
B.b<a<c
C.a<c<b
D.c<b<a
3.若正多边形的中心角为72°,则该正多边形的边数为( )
A.8
B.7
C.6
D.5
二.填空题(共2小题)
4.如图,在同一平面内,将边长相等的正方形、正五边形的一边重合,那么∠1=
°.
5.如图,以AB为边,在AB的同侧分别作正五边形ABCDE和等边△ABF,连接FE,FC,则∠EFA的度数是
.
三.解答题(共1小题)
6.如图,已知点O是正六边形ABCDEF的对称中心,G,H分别是AF,BC上的点,且AG=BH.
(1)求∠FAB的度数;
(2)求证:OG=OH.
24.3
正多边形和圆
参考答案与试题解析
一.选择题(共3小题)
1.下列说法中正确的是( )
A.直角三角形只有一条高
B.三角形任意两个内角的和大于第3个内角
C.在同圆中任意两条直径都互相平分
D.如果一个多边形的各边都相等,那么它是正多边形
【分析】利用直角三角形的性质、三角形的内角、圆的性质及正多边形的定义分别判断后即可确定正确的选项.
【解答】解:A、直角三角形有3条高,故原命题错误,不符合题意;
B、钝角三角形的两个较小的锐角的和小于最大的钝角,故原命题错误,不符合题意;
C、在同圆中任意两条直径都互相平分,正确,符合题意;
D、如果一个多边形的各角相等,各边都相等,那么它是正多边形,故原命题错误,不符合题意;
故选:C.
【点评】本题考查了正多边形和圆的知识,解题的关键是了解直角三角形的性质、三角形的内角、圆的性质及正多边形的定义等知识,难度不大.
2.半径为R的圆内接正三角形、正方形、正六边形的边心距分别为a,b,c,则a,b,c的大小关系是( )
A.a<b<c
B.b<a<c
C.a<c<b
D.c<b<a
【分析】根据三角函数即可求解.
【解答】解:设圆的半径为R,
则正三角形的边心距为a=R×cos60°=R.
四边形的边心距为b=R×cos45°=R,
正六边形的边心距为c=R×cos30°=R.
∵RRR,
∴a<b<c,
故选:A.
【点评】此题主要考查了正多边形和圆的性质,解决本题的关键是构造直角三角形,得到用半径表示的边心距;注意:正多边形的计算一般要转化为解直角三角形的问题来解决.
3.若正多边形的中心角为72°,则该正多边形的边数为( )
A.8
B.7
C.6
D.5
【分析】根据正多边形的中心角=,求出n即可.
【解答】解:由题意,=72°,
∴n=5,
故选:D.
【点评】本题考查正多边形的中心角知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
二.填空题(共2小题)
4.如图,在同一平面内,将边长相等的正方形、正五边形的一边重合,那么∠1= 18 °.
【分析】∠1的度数是正五边形的内角与正方形的内角的度数的差,根据多边形的内角和定理求得角的度数即可得出结果.
【解答】解:∵正五边形的内角的度数是
×(5﹣2)×180°=108°,
又∵正方形的内角是90°,
∴∠1=108°﹣90°=18°;
故答案为:18.
【点评】本题考查了正多边形和圆,多边形的内角和定理、正方形的性质,求得正五边形的内角的度数是关键.
5.如图,以AB为边,在AB的同侧分别作正五边形ABCDE和等边△ABF,连接FE,FC,则∠EFA的度数是 66° .
【分析】根据正五边形和等边三角形的性质得到∠EAF=108°﹣60°=48°,根据等腰三角形的性质即可得到结论.
【解答】解:∵正五边形ABCDE,
∴∠EAB==108°,
∵△ABF是等边三角形,
∴∠FAB=60°,
∴∠EAF=108°﹣60°=48°,
∵AE=AF,
∴∠AEF=∠AFE=(180°﹣48°)=66°,
故答案为:66°.
【点评】本题考查了正多边形与圆,正五边形和等边三角形的性质,等腰三角形的性质,正确的识别图形是解题的关键.
三.解答题(共1小题)
6.如图,已知点O是正六边形ABCDEF的对称中心,G,H分别是AF,BC上的点,且AG=BH.
(1)求∠FAB的度数;
(2)求证:OG=OH.
【分析】(1)根据多边形的内角和定理、正多边形的性质计算;
(2)证明△AOG≌△BOH,根据全等三角形的性质证明结论.
【解答】(1)解:∵六边形ABCDEF是正六边形,
∴∠FAB==120°;
(2)证明:连接OA、OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵∠FAB=∠CBA,
∴∠OAG=∠OBH,
在△AOG和△BOH中,
,
∴△AOG≌△BOH(SAS)
∴OG=OH.
【点评】本题考查的是正多边形和圆,掌握正多边形的内角的计算公式、全等三角形的判定定理和性质定理是解题的关键.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/9
9:10:32;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
同课章节目录
