24.1.1 圆的有关性质同步练习(含解析)
文档属性
| 名称 | 24.1.1 圆的有关性质同步练习(含解析) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 00:00:00 | ||
图片预览




文档简介
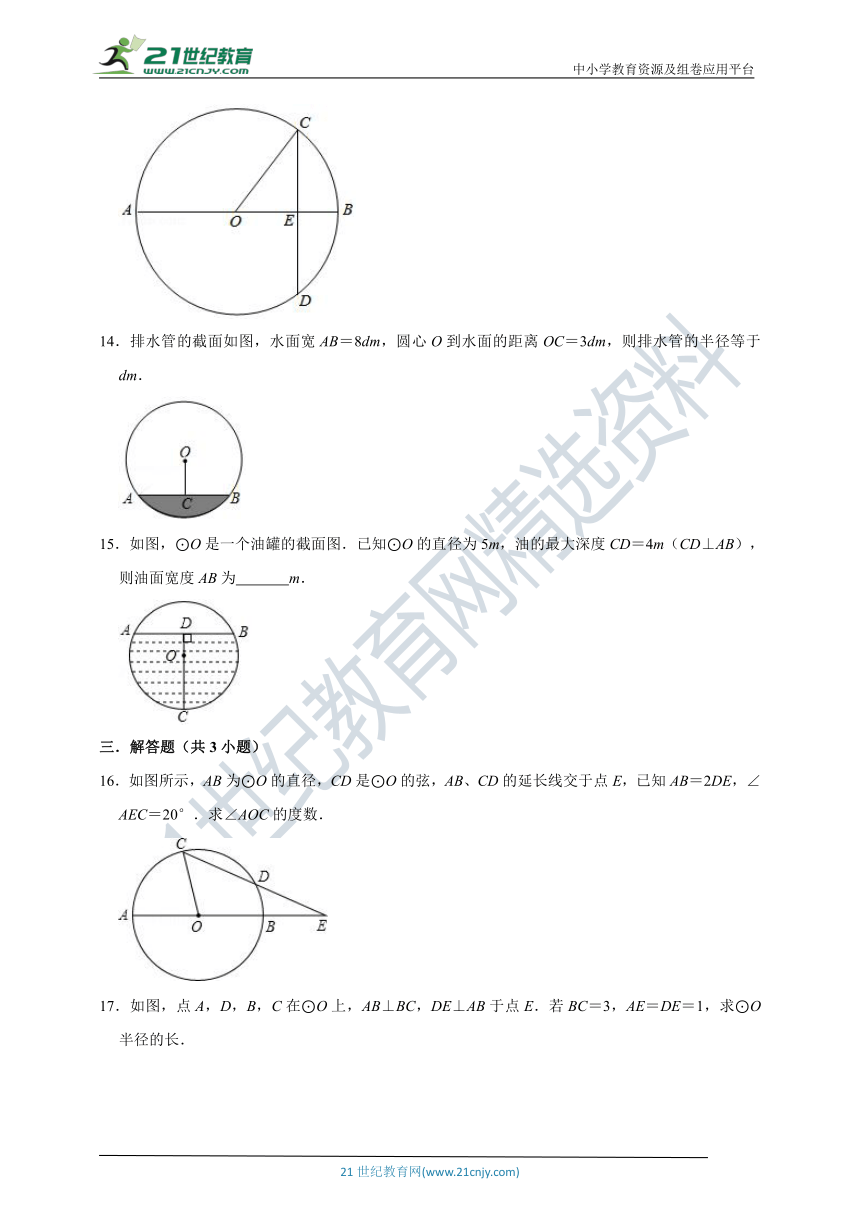
中小学教育资源及组卷应用平台
24.1
圆的有关性质(1)
一.选择题(共9小题)
1.下列说法正确的是( )
A.弦是直径
B.弧是半圆
C.直径是圆中最长的弦
D.半圆是圆中最长的弧
2.下列说法中,不正确的是( )
A.圆既是轴对称图形又是中心对称图形
B.圆的每一条直径都是它的对称轴
C.圆有无数条对称轴
D.圆的对称中心是它的圆心
3.已知⊙O的半径是5cm,则⊙O中最长的弦长是( )
A.5cm
B.10cm
C.15cm
D.20cm
4.如图所示,在半径为10cm的⊙O中,弦AB=16cm,OC⊥AB于点C,则OC等于( )
A.3cm
B.4cm
C.5cm
D.6cm
5.如图,△ABC中,AB=5,AC=4,BC=2,以A为圆心AB为半径作圆A,延长BC交圆A于点D,则CD长为( )
A.5
B.4
C.
D.2
6.在⊙O中,直径AB=15,弦DE⊥AB于点C,若OC:OB=3:5,则DE的长为( )
A.6
B.9
C.12
D.15
7.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm
B.10cm
C.16cm
D.20cm
8.一根水平放置的圆柱形输水管横截面如图所示,其中有水部分水面宽8米,最深处水深2米,则此输水管道的半径是( )
A.8米
B.6米
C.5米
D.4米
9.抛一个铁球,在泥地上砸了一个直径8cm,深2cm的坑,这个铁球的直径是( )
A.12cm
B.10cm
C.8cm
D.6cm
二.填空题(共6小题)
10.参加篝火晚会时,人们会自然围成一个圆,这是因为圆上任意一点到圆心的距离都
,这个距离就是这个圆的
.
11.如图,在半圆⊙O中,AB是直径,CD是一条弦,若AB=10,则△COD面积的最大值是
.
12.如图,有半径分别为2和4的两个同心圆,矩形ABCD的边AB,CD分别为两圆的弦,那么矩形ABCD面积的最大值为
.
13.如图AB是⊙O的直径,弦CD⊥OB于点E,交⊙O于点D,已知OC=5cm,CD=8cm,则AE=
cm.
14.排水管的截面如图,水面宽AB=8dm,圆心O到水面的距离OC=3dm,则排水管的半径等于
dm.
15.如图,⊙O是一个油罐的截面图.已知⊙O的直径为5m,油的最大深度CD=4m(CD⊥AB),则油面宽度AB为
m.
三.解答题(共3小题)
16.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
17.如图,点A,D,B,C在⊙O上,AB⊥BC,DE⊥AB于点E.若BC=3,AE=DE=1,求⊙O半径的长.
18.如图,在一座圆弧形拱桥,它的跨度AB为60m,拱高PM为18m,当洪水泛滥到跨度只有30m时,就要采取紧急措施,若某次洪水中,拱顶离水面只有4m,即PN=4m时,试通过计算说明是否需要采取紧急措施.
24.1
圆的有关性质(1)
参考答案与试题解析
一.选择题(共9小题)
1.下列说法正确的是( )
A.弦是直径
B.弧是半圆
C.直径是圆中最长的弦
D.半圆是圆中最长的弧
【分析】利用圆的有关概念及性质分别判断后即可确定正确的选项.
【解答】解:A、直径是弦,但弦不一定是直径,故错误,不符合题意;
B、半圆是弧,但弧不一定是半圆,故错误,不符合题意;
C、直径是圆中最长的弦,正确,符合题意;
D、半圆是小于优弧而大于劣弧的弧,故错误,不符合题意,
故选:C.
【点评】考查了圆的认识,解题的关键是正确的了解有关概念及性质,难度不大.
2.下列说法中,不正确的是( )
A.圆既是轴对称图形又是中心对称图形
B.圆的每一条直径都是它的对称轴
C.圆有无数条对称轴
D.圆的对称中心是它的圆心
【分析】结合圆的基本知识,逐一判断.
【解答】解:A.圆既是轴对称图形又是中心对称图形,正确;
B.圆的每一条直径所在直线都是它的对称轴,故B错误;
C.圆有无数条对称轴,正确;
D.圆的对称中心是它的圆心,正确.
故选:B.
【点评】本题考查了圆的对称性,熟练掌握圆的有关概念和性质是解题的关键.
3.已知⊙O的半径是5cm,则⊙O中最长的弦长是( )
A.5cm
B.10cm
C.15cm
D.20cm
【分析】根据圆中最长的弦是直径,且直径的长是半径长的2倍可得答案.
【解答】解:∵⊙O的半径是5cm,
∴⊙O中最长的弦,即直径的长为10cm,
故选:B.
【点评】本意主要考查圆的认识,解题的关键是掌握连接圆上任意两点的线段叫弦,经过圆心的弦叫直径,圆上任意两点间的部分叫圆弧,简称弧,圆的任意一条直径的两个端点把圆分成两条弧,每条弧都叫做半圆,大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧.
4.如图所示,在半径为10cm的⊙O中,弦AB=16cm,OC⊥AB于点C,则OC等于( )
A.3cm
B.4cm
C.5cm
D.6cm
【分析】根据垂径定理可知AC的长,再根据勾股定理即可求出OC的长.
【解答】解:连接OA,如图:
∵AB=16cm,OC⊥AB,
∴AC=AB=8cm,
在Rt△OAC中,OC===6(cm),
故选:D.
【点评】本题考查的是垂径定理、勾股定理,熟练掌握垂径定理,构造出直角三角形是解答此题的关键.
5.如图,△ABC中,AB=5,AC=4,BC=2,以A为圆心AB为半径作圆A,延长BC交圆A于点D,则CD长为( )
A.5
B.4
C.
D.2
【分析】如图,过点A作AE⊥BD于点E,连接AD,可得AD=AB=5,根据垂径定理可得DE=BE,得CE=BE﹣BC=DE﹣2,再根据勾股定理即可求得DE的长,进而可得CD的长.
【解答】解:如图,过点A作AE⊥BD于点E,连接AD,
∴AD=AB=5,
根据垂径定理,得
DE=BE,
∴CE=BE﹣BC=DE﹣2,
根据勾股定理,得
AD2﹣DE2=AC2﹣CE2,
∴52﹣DE2=42﹣(DE﹣2)2,
解得DE=,
∴CD=DE+CE=2DE﹣2=.
故选:C.
【点评】本题考查了垂径定理,解决本题的关键是掌握垂径定理.
6.在⊙O中,直径AB=15,弦DE⊥AB于点C,若OC:OB=3:5,则DE的长为( )
A.6
B.9
C.12
D.15
【分析】直接根据题意画出图形,再利用垂径定理以及勾股定理得出答案.
【解答】解:如图所示:连接OD,
∵直径AB=15,
∴BO=7.5,
∵OC:OB=3:5,
∴CO=4.5,
∴DC==6,
∴DE=2DC=12.
故选:C.
【点评】此题主要考查了垂径定理和勾股定理,正确得出CO的长是解题关键.
7.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm
B.10cm
C.16cm
D.20cm
【分析】连接OB,过点O作OC⊥AB于点D,交⊙O于点C,先由垂径定理求出BD的长,再根据勾股定理求出OD的长,进而可得出CD的长.
【解答】解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为52cm,
∴OB=OC=26cm,
在Rt△OBD中,OD===10(cm),
∴CD=OC﹣OD=26﹣10=16(cm),
故选:C.
【点评】本题考查了垂径定理、勾股定理等知识;根据题意作出辅助线,构造出直角三角形是解答此题的关键.
8.一根水平放置的圆柱形输水管横截面如图所示,其中有水部分水面宽8米,最深处水深2米,则此输水管道的半径是( )
A.8米
B.6米
C.5米
D.4米
【分析】连接OA,作OC⊥AB交AB于C,交圆于D,根据垂径定理求出AC,根据勾股定理列式计算,得到答案.
【解答】解:连接OA,作OC⊥AB交AB于C,交圆于D,
由题意得,AB=8,CD=2,
∵OC⊥AB,
∴AC=AB=4,
设圆的半径为r米,则OC=(r﹣2)米,
由勾股定理得,OA2=OC2+AC2,即r2=(r﹣2)2+42,
解得,r=5,即此输水管道的半径是5米,
故选:C.
【点评】本题考查的是垂径定理的应用、勾股定理,垂径定理和勾股定理相结合,构造直角三角形,可解决计算弦长、半径、弦心距等问题.
9.抛一个铁球,在泥地上砸了一个直径8cm,深2cm的坑,这个铁球的直径是( )
A.12cm
B.10cm
C.8cm
D.6cm
【分析】根据题意画出草图,建立数学模型.根据勾股定理和垂径定理求解.
【解答】解:设该铅球的半径是rcm.
在由铅球的半径、小坑的半径即半弦和弦心距组成的直角三角形中,
根据勾股定理,得r2=(r﹣2)2+16,
解得r=5,
故2r=10.
故选:B.
【点评】此题主要考查了勾股定理和垂径定理的应用,能够从实际问题中抽象出几何图形,再进一步根据勾股定理以及垂径定理进行计算是解题关键.
二.填空题(共6小题)
10.参加篝火晚会时,人们会自然围成一个圆,这是因为圆上任意一点到圆心的距离都 相等 ,这个距离就是这个圆的 半径 .
【分析】利用圆的性质得出圆上各点到圆心的距离等于半径,进而得出答案.
【解答】解:参加篝火晚会时,人们会自然围成一个圆,这是因为圆上任意一点到圆心的距离都相等,这个距离就是这个圆的半径.
故答案为:相等,半径.
【点评】此题主要考查了圆的认识,根据圆上各点到圆心的距离等于半径是解题关键.
11.如图,在半圆⊙O中,AB是直径,CD是一条弦,若AB=10,则△COD面积的最大值是 12.5 .
【分析】如图,作DH⊥CO交CO的延长线于H.首先证明当DH=OD时,△COD的面积最大,此时△COD是等腰直角三角形,然后求得最大值即可.
【解答】解:如图,作DH⊥CO交CO的延长线于H.
∵S△COD=?OC?DH,
∵DH≤OD,
∴当DH=OD时,△COD的面积最大,此时△COD是等腰直角三角形,∠COD=90°,
此时面积的最大值为:×5×5=12.5,
故答案为:12.5.
【点评】本题考查三角形的面积、等腰直角三角形的判定和性质,解题的关键是灵活运用所学知识解决问题.
12.如图,有半径分别为2和4的两个同心圆,矩形ABCD的边AB,CD分别为两圆的弦,那么矩形ABCD面积的最大值为 48 .
【分析】此题首先能够把问题转化到三角形中进行分析.根据锐角三角函数的概念可以证明三角形的面积等于相邻两边的乘积乘以夹角的正弦值,根据这一公式分析面积的最大值的情况.然后运用勾股定理以及直角三角形的斜边上的高等于两条直角边的乘积除以斜边求得长方形的长和宽,进一步求得其面积.
【解答】解:连接OA,OD,作OP⊥AB于P,OM⊥AD于M,ON⊥CD于N,
根据矩形的面积以及三角形的面积公式发现:矩形的面积是三角形AOD的面积的4倍.
因为OA,OD的长是定值,则∠AOD的正弦值最大时,三角形的面积最大,
即∠AOD=90°,则AD===6,
S△AOD==×OM==,
OM=4,即AB=8.
则矩形ABCD的面积的最大值是AB?AD=8×=48.
故答案为:48.
【点评】本题考查的是矩形的定理以及垂径的性质,解题的关键是注意运用勾股定理来求得边长继而才能求出面积.
13.如图AB是⊙O的直径,弦CD⊥OB于点E,交⊙O于点D,已知OC=5cm,CD=8cm,则AE= 8 cm.
【分析】利用垂径定理得到CE=DE=CD=4,然后利用勾股定理计算出OE,再计算AO+OE即可.
【解答】解:∵CD⊥OB,
∴CE=DE=CD=4,
在Rt△OCE中,OE==3,
∴AE=AO+OE=5+3=8(cm).
故答案为8.
【点评】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.
14.排水管的截面如图,水面宽AB=8dm,圆心O到水面的距离OC=3dm,则排水管的半径等于 5 dm.
【分析】连接OA,先根据垂径定理求出AC的长,再由勾股定理求出OA的长即可.
【解答】解:连接OA,
∵AB=8,OC⊥AB,
∴AC=AB=4.
∵OC=3,
∴OA===5(dm).
故答案为:5.
【点评】本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.
15.如图,⊙O是一个油罐的截面图.已知⊙O的直径为5m,油的最大深度CD=4m(CD⊥AB),则油面宽度AB为 4 m.
【分析】根据垂径定理和勾股定理进行解答即可.
【解答】解:连接OA,
由题意得,OA=2.5m,OD=1.5m,
∵CD⊥AB,
∴AD==2m,
∴AB=2AD=4m,
故答案为:4.
【点评】此题考查了垂径定理的应用.此题难度不大,解题的关键是注意数形结合思想的应用.
三.解答题(共3小题)
16.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
【分析】连接OD,如图,由AB=2DE,AB=2OD得到OD=DE,根据等腰三角形的性质得∠DOE=∠E=20°,再利用三角形外角性质得到∠CDO=40°,加上∠C=∠ODC=40°,然后再利用三角形外角性质即可计算出∠AOC.
【解答】解:连接OD,如图,
∵AB=2DE,
而AB=2OD,
∴OD=DE,
∴∠DOE=∠E=20°,
∴∠CDO=∠DOE+∠E=40°,
而OC=OD,
∴∠C=∠ODC=40°,
∴∠AOC=∠C+∠E=60°.
【点评】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质.
17.如图,点A,D,B,C在⊙O上,AB⊥BC,DE⊥AB于点E.若BC=3,AE=DE=1,求⊙O半径的长.
【分析】直接利用圆周角定理结合等腰直角三角形的性质得出AB的长,再利用勾股定理得出答案.
【解答】解:如图,连接AD,AC,连接CD与AB交于点F,
∵AB⊥BC,
∴∠ABC=90°.
∴AC为直径.
∴∠ADC=90°.
∵AE=DE,DE⊥AB,
∴∠DAB=∠ADE=45°.
∴∠BCF=∠DAB=45°.
∴BC=BF=3.
在△ADF中,∠DAB=∠AFD=45°,
∴EF=ED=1.
∴AB=5.
∴AC==.
∴⊙O半径的长.
【点评】此题主要考查了勾股定理以及垂径定理,正确得出AB的长是解题关键.
18.如图,在一座圆弧形拱桥,它的跨度AB为60m,拱高PM为18m,当洪水泛滥到跨度只有30m时,就要采取紧急措施,若某次洪水中,拱顶离水面只有4m,即PN=4m时,试通过计算说明是否需要采取紧急措施.
【分析】由垂径定理可知AM=BM、A′N=B′N,利用AB=60,PM=18,可先求得圆弧所在圆的半径,再计算当PN=4时A′B′的长度,与30米进行比较大小即可.
【解答】解:设圆弧所在圆的圆心为O,连接OA、OA′,设半径为x米,
则OA=OA′=OP,
由垂径定理可知AM=BM,A′N=B′N,
∵AB=60米,
∴AM=30米,且OM=OP﹣PM=(x﹣18)米,
在Rt△AOM中,由勾股定理可得AO2=OM2+AM2,
即x2=(x﹣18)2+302,解得x=34,
∴ON=OP﹣PN=34﹣4=30(米),
在Rt△A′ON中,由勾股定理可得A′N===16(米),
∴A′B′=32米>30米,
∴不需要采取紧急措施.
【点评】本题主要考查垂径定理的应用,利用勾股定理求得圆弧所在的半径是解题的关键,注意方程思想的应用.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/8
10:31:49;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
24.1
圆的有关性质(1)
一.选择题(共9小题)
1.下列说法正确的是( )
A.弦是直径
B.弧是半圆
C.直径是圆中最长的弦
D.半圆是圆中最长的弧
2.下列说法中,不正确的是( )
A.圆既是轴对称图形又是中心对称图形
B.圆的每一条直径都是它的对称轴
C.圆有无数条对称轴
D.圆的对称中心是它的圆心
3.已知⊙O的半径是5cm,则⊙O中最长的弦长是( )
A.5cm
B.10cm
C.15cm
D.20cm
4.如图所示,在半径为10cm的⊙O中,弦AB=16cm,OC⊥AB于点C,则OC等于( )
A.3cm
B.4cm
C.5cm
D.6cm
5.如图,△ABC中,AB=5,AC=4,BC=2,以A为圆心AB为半径作圆A,延长BC交圆A于点D,则CD长为( )
A.5
B.4
C.
D.2
6.在⊙O中,直径AB=15,弦DE⊥AB于点C,若OC:OB=3:5,则DE的长为( )
A.6
B.9
C.12
D.15
7.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm
B.10cm
C.16cm
D.20cm
8.一根水平放置的圆柱形输水管横截面如图所示,其中有水部分水面宽8米,最深处水深2米,则此输水管道的半径是( )
A.8米
B.6米
C.5米
D.4米
9.抛一个铁球,在泥地上砸了一个直径8cm,深2cm的坑,这个铁球的直径是( )
A.12cm
B.10cm
C.8cm
D.6cm
二.填空题(共6小题)
10.参加篝火晚会时,人们会自然围成一个圆,这是因为圆上任意一点到圆心的距离都
,这个距离就是这个圆的
.
11.如图,在半圆⊙O中,AB是直径,CD是一条弦,若AB=10,则△COD面积的最大值是
.
12.如图,有半径分别为2和4的两个同心圆,矩形ABCD的边AB,CD分别为两圆的弦,那么矩形ABCD面积的最大值为
.
13.如图AB是⊙O的直径,弦CD⊥OB于点E,交⊙O于点D,已知OC=5cm,CD=8cm,则AE=
cm.
14.排水管的截面如图,水面宽AB=8dm,圆心O到水面的距离OC=3dm,则排水管的半径等于
dm.
15.如图,⊙O是一个油罐的截面图.已知⊙O的直径为5m,油的最大深度CD=4m(CD⊥AB),则油面宽度AB为
m.
三.解答题(共3小题)
16.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
17.如图,点A,D,B,C在⊙O上,AB⊥BC,DE⊥AB于点E.若BC=3,AE=DE=1,求⊙O半径的长.
18.如图,在一座圆弧形拱桥,它的跨度AB为60m,拱高PM为18m,当洪水泛滥到跨度只有30m时,就要采取紧急措施,若某次洪水中,拱顶离水面只有4m,即PN=4m时,试通过计算说明是否需要采取紧急措施.
24.1
圆的有关性质(1)
参考答案与试题解析
一.选择题(共9小题)
1.下列说法正确的是( )
A.弦是直径
B.弧是半圆
C.直径是圆中最长的弦
D.半圆是圆中最长的弧
【分析】利用圆的有关概念及性质分别判断后即可确定正确的选项.
【解答】解:A、直径是弦,但弦不一定是直径,故错误,不符合题意;
B、半圆是弧,但弧不一定是半圆,故错误,不符合题意;
C、直径是圆中最长的弦,正确,符合题意;
D、半圆是小于优弧而大于劣弧的弧,故错误,不符合题意,
故选:C.
【点评】考查了圆的认识,解题的关键是正确的了解有关概念及性质,难度不大.
2.下列说法中,不正确的是( )
A.圆既是轴对称图形又是中心对称图形
B.圆的每一条直径都是它的对称轴
C.圆有无数条对称轴
D.圆的对称中心是它的圆心
【分析】结合圆的基本知识,逐一判断.
【解答】解:A.圆既是轴对称图形又是中心对称图形,正确;
B.圆的每一条直径所在直线都是它的对称轴,故B错误;
C.圆有无数条对称轴,正确;
D.圆的对称中心是它的圆心,正确.
故选:B.
【点评】本题考查了圆的对称性,熟练掌握圆的有关概念和性质是解题的关键.
3.已知⊙O的半径是5cm,则⊙O中最长的弦长是( )
A.5cm
B.10cm
C.15cm
D.20cm
【分析】根据圆中最长的弦是直径,且直径的长是半径长的2倍可得答案.
【解答】解:∵⊙O的半径是5cm,
∴⊙O中最长的弦,即直径的长为10cm,
故选:B.
【点评】本意主要考查圆的认识,解题的关键是掌握连接圆上任意两点的线段叫弦,经过圆心的弦叫直径,圆上任意两点间的部分叫圆弧,简称弧,圆的任意一条直径的两个端点把圆分成两条弧,每条弧都叫做半圆,大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧.
4.如图所示,在半径为10cm的⊙O中,弦AB=16cm,OC⊥AB于点C,则OC等于( )
A.3cm
B.4cm
C.5cm
D.6cm
【分析】根据垂径定理可知AC的长,再根据勾股定理即可求出OC的长.
【解答】解:连接OA,如图:
∵AB=16cm,OC⊥AB,
∴AC=AB=8cm,
在Rt△OAC中,OC===6(cm),
故选:D.
【点评】本题考查的是垂径定理、勾股定理,熟练掌握垂径定理,构造出直角三角形是解答此题的关键.
5.如图,△ABC中,AB=5,AC=4,BC=2,以A为圆心AB为半径作圆A,延长BC交圆A于点D,则CD长为( )
A.5
B.4
C.
D.2
【分析】如图,过点A作AE⊥BD于点E,连接AD,可得AD=AB=5,根据垂径定理可得DE=BE,得CE=BE﹣BC=DE﹣2,再根据勾股定理即可求得DE的长,进而可得CD的长.
【解答】解:如图,过点A作AE⊥BD于点E,连接AD,
∴AD=AB=5,
根据垂径定理,得
DE=BE,
∴CE=BE﹣BC=DE﹣2,
根据勾股定理,得
AD2﹣DE2=AC2﹣CE2,
∴52﹣DE2=42﹣(DE﹣2)2,
解得DE=,
∴CD=DE+CE=2DE﹣2=.
故选:C.
【点评】本题考查了垂径定理,解决本题的关键是掌握垂径定理.
6.在⊙O中,直径AB=15,弦DE⊥AB于点C,若OC:OB=3:5,则DE的长为( )
A.6
B.9
C.12
D.15
【分析】直接根据题意画出图形,再利用垂径定理以及勾股定理得出答案.
【解答】解:如图所示:连接OD,
∵直径AB=15,
∴BO=7.5,
∵OC:OB=3:5,
∴CO=4.5,
∴DC==6,
∴DE=2DC=12.
故选:C.
【点评】此题主要考查了垂径定理和勾股定理,正确得出CO的长是解题关键.
7.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm
B.10cm
C.16cm
D.20cm
【分析】连接OB,过点O作OC⊥AB于点D,交⊙O于点C,先由垂径定理求出BD的长,再根据勾股定理求出OD的长,进而可得出CD的长.
【解答】解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为52cm,
∴OB=OC=26cm,
在Rt△OBD中,OD===10(cm),
∴CD=OC﹣OD=26﹣10=16(cm),
故选:C.
【点评】本题考查了垂径定理、勾股定理等知识;根据题意作出辅助线,构造出直角三角形是解答此题的关键.
8.一根水平放置的圆柱形输水管横截面如图所示,其中有水部分水面宽8米,最深处水深2米,则此输水管道的半径是( )
A.8米
B.6米
C.5米
D.4米
【分析】连接OA,作OC⊥AB交AB于C,交圆于D,根据垂径定理求出AC,根据勾股定理列式计算,得到答案.
【解答】解:连接OA,作OC⊥AB交AB于C,交圆于D,
由题意得,AB=8,CD=2,
∵OC⊥AB,
∴AC=AB=4,
设圆的半径为r米,则OC=(r﹣2)米,
由勾股定理得,OA2=OC2+AC2,即r2=(r﹣2)2+42,
解得,r=5,即此输水管道的半径是5米,
故选:C.
【点评】本题考查的是垂径定理的应用、勾股定理,垂径定理和勾股定理相结合,构造直角三角形,可解决计算弦长、半径、弦心距等问题.
9.抛一个铁球,在泥地上砸了一个直径8cm,深2cm的坑,这个铁球的直径是( )
A.12cm
B.10cm
C.8cm
D.6cm
【分析】根据题意画出草图,建立数学模型.根据勾股定理和垂径定理求解.
【解答】解:设该铅球的半径是rcm.
在由铅球的半径、小坑的半径即半弦和弦心距组成的直角三角形中,
根据勾股定理,得r2=(r﹣2)2+16,
解得r=5,
故2r=10.
故选:B.
【点评】此题主要考查了勾股定理和垂径定理的应用,能够从实际问题中抽象出几何图形,再进一步根据勾股定理以及垂径定理进行计算是解题关键.
二.填空题(共6小题)
10.参加篝火晚会时,人们会自然围成一个圆,这是因为圆上任意一点到圆心的距离都 相等 ,这个距离就是这个圆的 半径 .
【分析】利用圆的性质得出圆上各点到圆心的距离等于半径,进而得出答案.
【解答】解:参加篝火晚会时,人们会自然围成一个圆,这是因为圆上任意一点到圆心的距离都相等,这个距离就是这个圆的半径.
故答案为:相等,半径.
【点评】此题主要考查了圆的认识,根据圆上各点到圆心的距离等于半径是解题关键.
11.如图,在半圆⊙O中,AB是直径,CD是一条弦,若AB=10,则△COD面积的最大值是 12.5 .
【分析】如图,作DH⊥CO交CO的延长线于H.首先证明当DH=OD时,△COD的面积最大,此时△COD是等腰直角三角形,然后求得最大值即可.
【解答】解:如图,作DH⊥CO交CO的延长线于H.
∵S△COD=?OC?DH,
∵DH≤OD,
∴当DH=OD时,△COD的面积最大,此时△COD是等腰直角三角形,∠COD=90°,
此时面积的最大值为:×5×5=12.5,
故答案为:12.5.
【点评】本题考查三角形的面积、等腰直角三角形的判定和性质,解题的关键是灵活运用所学知识解决问题.
12.如图,有半径分别为2和4的两个同心圆,矩形ABCD的边AB,CD分别为两圆的弦,那么矩形ABCD面积的最大值为 48 .
【分析】此题首先能够把问题转化到三角形中进行分析.根据锐角三角函数的概念可以证明三角形的面积等于相邻两边的乘积乘以夹角的正弦值,根据这一公式分析面积的最大值的情况.然后运用勾股定理以及直角三角形的斜边上的高等于两条直角边的乘积除以斜边求得长方形的长和宽,进一步求得其面积.
【解答】解:连接OA,OD,作OP⊥AB于P,OM⊥AD于M,ON⊥CD于N,
根据矩形的面积以及三角形的面积公式发现:矩形的面积是三角形AOD的面积的4倍.
因为OA,OD的长是定值,则∠AOD的正弦值最大时,三角形的面积最大,
即∠AOD=90°,则AD===6,
S△AOD==×OM==,
OM=4,即AB=8.
则矩形ABCD的面积的最大值是AB?AD=8×=48.
故答案为:48.
【点评】本题考查的是矩形的定理以及垂径的性质,解题的关键是注意运用勾股定理来求得边长继而才能求出面积.
13.如图AB是⊙O的直径,弦CD⊥OB于点E,交⊙O于点D,已知OC=5cm,CD=8cm,则AE= 8 cm.
【分析】利用垂径定理得到CE=DE=CD=4,然后利用勾股定理计算出OE,再计算AO+OE即可.
【解答】解:∵CD⊥OB,
∴CE=DE=CD=4,
在Rt△OCE中,OE==3,
∴AE=AO+OE=5+3=8(cm).
故答案为8.
【点评】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.
14.排水管的截面如图,水面宽AB=8dm,圆心O到水面的距离OC=3dm,则排水管的半径等于 5 dm.
【分析】连接OA,先根据垂径定理求出AC的长,再由勾股定理求出OA的长即可.
【解答】解:连接OA,
∵AB=8,OC⊥AB,
∴AC=AB=4.
∵OC=3,
∴OA===5(dm).
故答案为:5.
【点评】本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.
15.如图,⊙O是一个油罐的截面图.已知⊙O的直径为5m,油的最大深度CD=4m(CD⊥AB),则油面宽度AB为 4 m.
【分析】根据垂径定理和勾股定理进行解答即可.
【解答】解:连接OA,
由题意得,OA=2.5m,OD=1.5m,
∵CD⊥AB,
∴AD==2m,
∴AB=2AD=4m,
故答案为:4.
【点评】此题考查了垂径定理的应用.此题难度不大,解题的关键是注意数形结合思想的应用.
三.解答题(共3小题)
16.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
【分析】连接OD,如图,由AB=2DE,AB=2OD得到OD=DE,根据等腰三角形的性质得∠DOE=∠E=20°,再利用三角形外角性质得到∠CDO=40°,加上∠C=∠ODC=40°,然后再利用三角形外角性质即可计算出∠AOC.
【解答】解:连接OD,如图,
∵AB=2DE,
而AB=2OD,
∴OD=DE,
∴∠DOE=∠E=20°,
∴∠CDO=∠DOE+∠E=40°,
而OC=OD,
∴∠C=∠ODC=40°,
∴∠AOC=∠C+∠E=60°.
【点评】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质.
17.如图,点A,D,B,C在⊙O上,AB⊥BC,DE⊥AB于点E.若BC=3,AE=DE=1,求⊙O半径的长.
【分析】直接利用圆周角定理结合等腰直角三角形的性质得出AB的长,再利用勾股定理得出答案.
【解答】解:如图,连接AD,AC,连接CD与AB交于点F,
∵AB⊥BC,
∴∠ABC=90°.
∴AC为直径.
∴∠ADC=90°.
∵AE=DE,DE⊥AB,
∴∠DAB=∠ADE=45°.
∴∠BCF=∠DAB=45°.
∴BC=BF=3.
在△ADF中,∠DAB=∠AFD=45°,
∴EF=ED=1.
∴AB=5.
∴AC==.
∴⊙O半径的长.
【点评】此题主要考查了勾股定理以及垂径定理,正确得出AB的长是解题关键.
18.如图,在一座圆弧形拱桥,它的跨度AB为60m,拱高PM为18m,当洪水泛滥到跨度只有30m时,就要采取紧急措施,若某次洪水中,拱顶离水面只有4m,即PN=4m时,试通过计算说明是否需要采取紧急措施.
【分析】由垂径定理可知AM=BM、A′N=B′N,利用AB=60,PM=18,可先求得圆弧所在圆的半径,再计算当PN=4时A′B′的长度,与30米进行比较大小即可.
【解答】解:设圆弧所在圆的圆心为O,连接OA、OA′,设半径为x米,
则OA=OA′=OP,
由垂径定理可知AM=BM,A′N=B′N,
∵AB=60米,
∴AM=30米,且OM=OP﹣PM=(x﹣18)米,
在Rt△AOM中,由勾股定理可得AO2=OM2+AM2,
即x2=(x﹣18)2+302,解得x=34,
∴ON=OP﹣PN=34﹣4=30(米),
在Rt△A′ON中,由勾股定理可得A′N===16(米),
∴A′B′=32米>30米,
∴不需要采取紧急措施.
【点评】本题主要考查垂径定理的应用,利用勾股定理求得圆弧所在的半径是解题的关键,注意方程思想的应用.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/8
10:31:49;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
同课章节目录
