24.2.2 直线和圆的位置关系(2)同步练习(含解析)
文档属性
| 名称 | 24.2.2 直线和圆的位置关系(2)同步练习(含解析) |  | |
| 格式 | rar | ||
| 文件大小 | 554.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 21:11:59 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
24.2.2
直线和圆的位置关系(2)
一.选择题(共9小题)
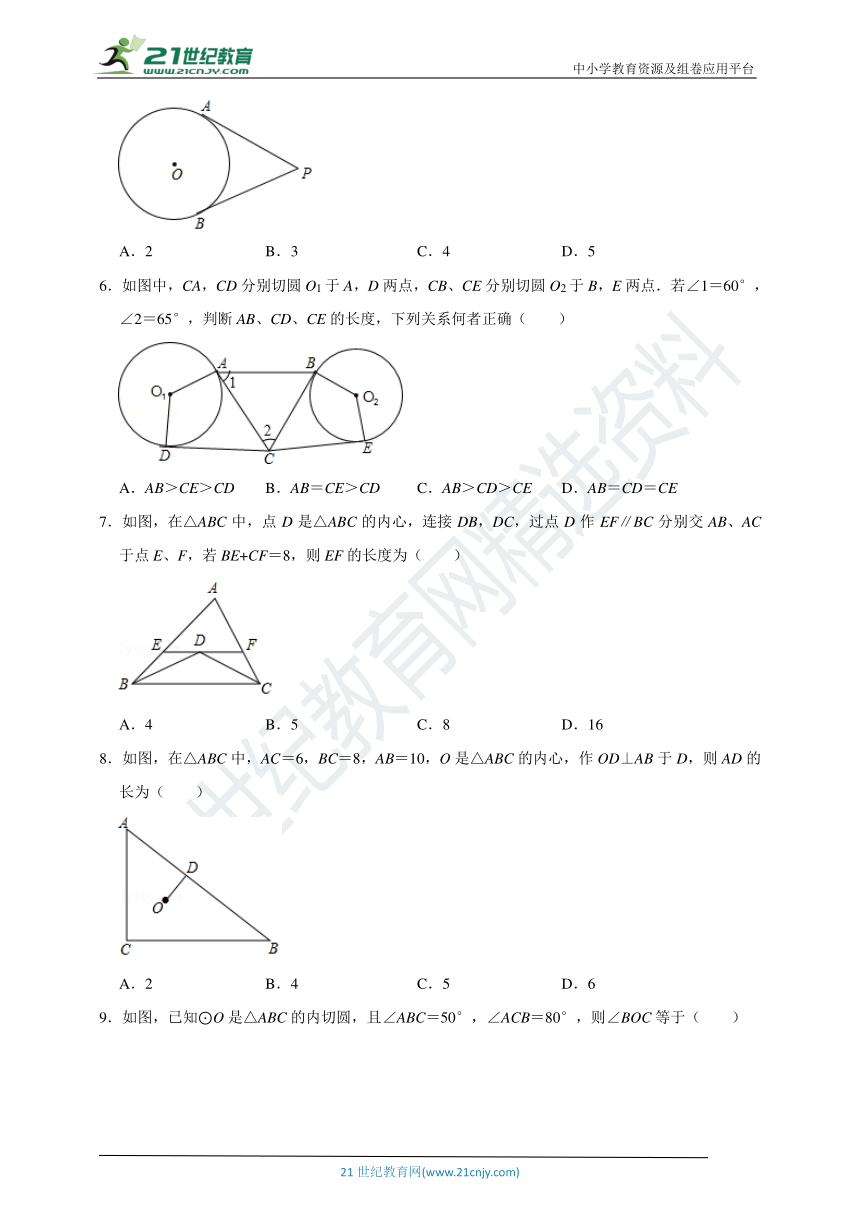
1.如图,在矩形ABCD中,BC=8,以AB为直径作⊙O,将矩形ABCD绕点B旋转,使所得矩形A'BC'D'的边C'D'与⊙O相切,切点为E,边A'B与⊙O相交于点F.若BF=8,则CD长为( )
A.9
B.10
C.8
D.12
2.如图,在直线l上有相距7cm的两点A和O(点A在点O的右侧),以O为圆心作半径为1cm的圆,过点A作直线AB⊥l.将⊙O以2cm/s的速度向右移动(点O始终在直线l上),则⊙O与直线AB在( )秒时相切.
A.3
B.3.5
C.3或4
D.3或3.5
3.已知圆O的半径为R,点O到直线m的距离为d、R、d是方程x2﹣4x+a=0的两根,当直线m与圆O相切时,a的值是( )
A.3
B.4
C.5
D.无法确定
4.如图,是用一把直尺、含60°角的直角三角板和光盘摆放而成,点A为60°角与直尺交点,点B为光盘与直尺唯一交点,若AB=3,则光盘的直径是( )
A.6
B.3
C.6
D.3
5.如图,P为圆O外一点,PA,PB分别切圆O于A,B两点,若PA=3,则PB=( )
A.2
B.3
C.4
D.5
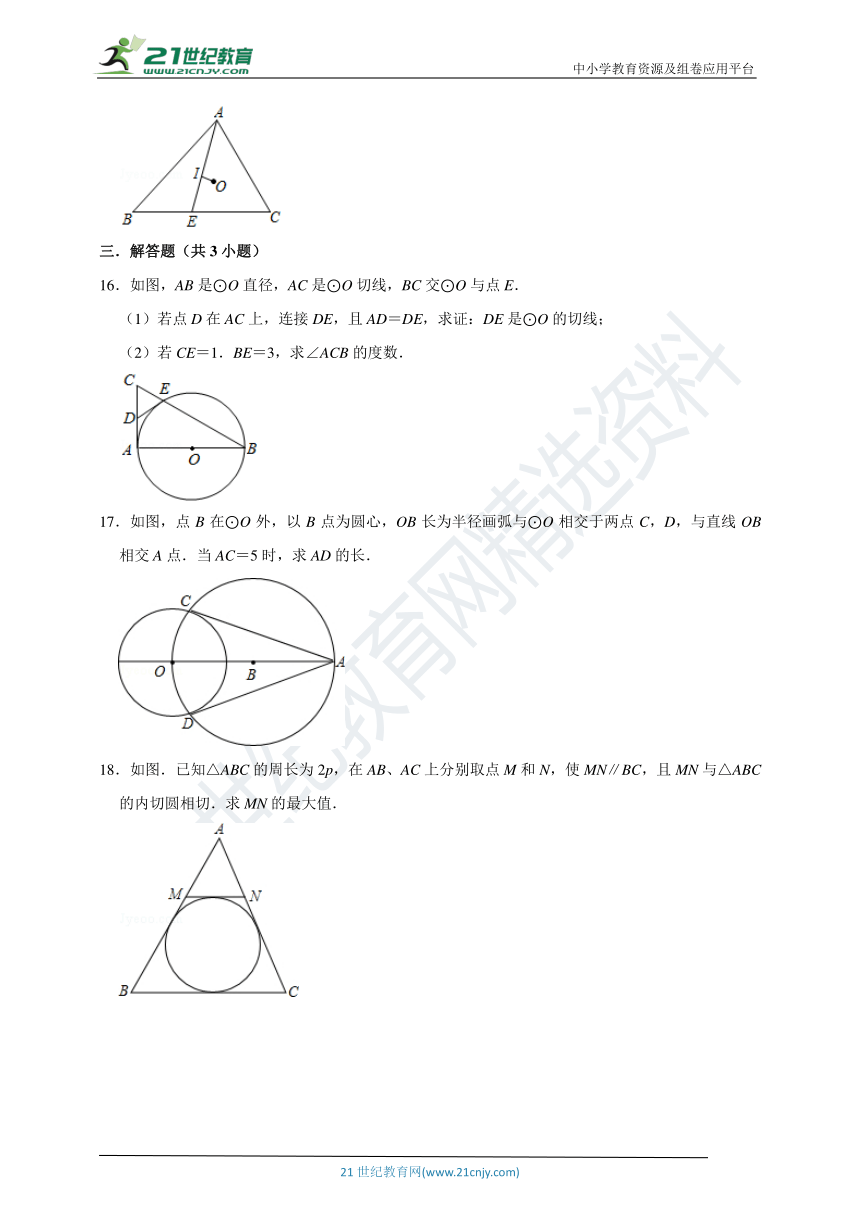
6.如图中,CA,CD分别切圆O1于A,D两点,CB、CE分别切圆O2于B,E两点.若∠1=60°,∠2=65°,判断AB、CD、CE的长度,下列关系何者正确( )
A.AB>CE>CD
B.AB=CE>CD
C.AB>CD>CE
D.AB=CD=CE
7.如图,在△ABC中,点D是△ABC的内心,连接DB,DC,过点D作EF∥BC分别交AB、AC于点E、F,若BE+CF=8,则EF的长度为( )
A.4
B.5
C.8
D.16
8.如图,在△ABC中,AC=6,BC=8,AB=10,O是△ABC的内心,作OD⊥AB于D,则AD的长为( )
A.2
B.4
C.5
D.6
9.如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC等于( )
A.125°
B.120°
C.115°
D.110°
二.填空题(共6小题)
10.如图,在矩形ABCD中,AB=3,BC=4,P是对角线AC上的动点,以点P为圆心,PC长为半径作⊙P.当⊙P与矩形ABCD的边相切时,CP的长为
.
11.直线l经过点A
(4,0),B(0,2),若⊙M的半径为1,圆心M在x轴上,当⊙M与直线l相切时,则点M的坐标
.
12.一个菱形的周长是20cm,两对角线之比是4:3,则该菱形的内切圆的半径是
cm.
13.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=15,则四边形ABCD的周长为
.
14.如图,在△ABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆半径r=
.
15.如图,△ABC为锐角三角形,I为内心,O为外心,若OI⊥AI,AB=4,则BE=
.
三.解答题(共3小题)
16.如图,AB是⊙O直径,AC是⊙O切线,BC交⊙O与点E.
(1)若点D在AC上,连接DE,且AD=DE,求证:DE是⊙O的切线;
(2)若CE=1.BE=3,求∠ACB的度数.
17.如图,点B在⊙O外,以B点为圆心,OB长为半径画弧与⊙O相交于两点C,D,与直线OB相交A点.当AC=5时,求AD的长.
18.如图.已知△ABC的周长为2p,在AB、AC上分别取点M和N,使MN∥BC,且MN与△ABC的内切圆相切.求MN的最大值.
24.2.2
直线和圆的位置关系(2)
参考答案与试题解析
一.选择题(共9小题)
1.如图,在矩形ABCD中,BC=8,以AB为直径作⊙O,将矩形ABCD绕点B旋转,使所得矩形A'BC'D'的边C'D'与⊙O相切,切点为E,边A'B与⊙O相交于点F.若BF=8,则CD长为( )
A.9
B.10
C.8
D.12
【分析】连接OE,延长EO交BF于点M,设OB=OE=x,则OM=8﹣x,由勾股定理得出(8﹣x)2+42=x2,解得x=5,则得出答案.
【解答】解:连接OE,延长EO交BF于点M,
∵C'D'与⊙O相切,
∴∠OEC′=90°,
又矩形A'BC'D'中,A'B∥C'D',
∴∠EMB=90°,
∴BM=FM,
∵矩形ABCD绕点B旋转所得矩形为A′BC′D′,
∴∠C′=∠C=90°,AB=CD,BC=B′C=8,
∴四边形EMBC'为矩形,
∴ME=8,
设OB=OE=x,则OM=8﹣x,
∵OM2+BM2=OB2,
∴(8﹣x)2+42=x2,
解得x=5,
∴AB=CD=10.
故选:B.
【点评】本题主要考查圆的切线的判定与性质,解题的关键是掌握矩形的判定与性质、旋转的性质、切线的性质、垂径定理等知识点.
2.如图,在直线l上有相距7cm的两点A和O(点A在点O的右侧),以O为圆心作半径为1cm的圆,过点A作直线AB⊥l.将⊙O以2cm/s的速度向右移动(点O始终在直线l上),则⊙O与直线AB在( )秒时相切.
A.3
B.3.5
C.3或4
D.3或3.5
【分析】根据切线的判定方法,当点O到AB的距离为1cm时,⊙O与AB相切,然后计算出圆向右移动的距离,然后计算出对应的时间.
【解答】解:当点O到AB的距离为1cm时,⊙O与AB相切,
∵开始时O点到AB的距离为7,
∴当圆向右移动7﹣1或7+1时,点O到AB的距离为1cm,此时⊙O与AB相切,
∴t==3(s)或t==4(s),
即⊙O与直线AB在3秒或4秒时相切.
故选:C.
【点评】本题考查了切线的判定与性质:圆的切线垂直于经过切点的半径;经过半径的外端且垂直于这条半径的直线是圆的切线,当圆心到直线的距离等于圆的半径,则直线与圆相切.
3.已知圆O的半径为R,点O到直线m的距离为d、R、d是方程x2﹣4x+a=0的两根,当直线m与圆O相切时,a的值是( )
A.3
B.4
C.5
D.无法确定
【分析】若直线和圆相切,则d=R.即方程有两个相等的实数根,得16﹣4a=0,可得a=4.
【解答】解:∵直线和圆相切,
∴d=R,
∴△=16﹣4a=0,
∴a=4,
故选:B.
【点评】此题考查了直线和圆的位置关系与数量关系之间的联系,关键是熟练运用根的判别式判断方程的根的情况.
4.如图,是用一把直尺、含60°角的直角三角板和光盘摆放而成,点A为60°角与直尺交点,点B为光盘与直尺唯一交点,若AB=3,则光盘的直径是( )
A.6
B.3
C.6
D.3
【分析】设三角板与圆的切点为C,连接OA、OB,由切线长定理得出AB=AC=3、∠OAB=60°,根据OB=ABtan∠OAB可得答案.
【解答】解:设三角板与圆的切点为C,连接OA、OB,
由切线长定理知AB=AC=3,OA平分∠BAC,
∴∠OAB=60°,
在Rt△ABO中,OB=ABtan∠OAB=3,
∴光盘的直径为6,
故选:A.
【点评】本题主要考查切线的性质,解题的关键是掌握切线长定理和解直角三角形的应用.
5.如图,P为圆O外一点,PA,PB分别切圆O于A,B两点,若PA=3,则PB=( )
A.2
B.3
C.4
D.5
【分析】连接OA、OB、OP,根据切线的性质得出OA⊥PA,OB⊥PB,即可求得PB=PA=3.
【解答】解:连接OA,OB,OP,
∵PA,PB分别切圆O于A,B两点,
∴OA⊥PA,OB⊥PB,
∴PB=PA=3,
故选:B.
【点评】本题考查了切线长定理,三角形全等的判定和性质,作出辅助线根据全等三角形是解题的关键.
6.如图中,CA,CD分别切圆O1于A,D两点,CB、CE分别切圆O2于B,E两点.若∠1=60°,∠2=65°,判断AB、CD、CE的长度,下列关系何者正确( )
A.AB>CE>CD
B.AB=CE>CD
C.AB>CD>CE
D.AB=CD=CE
【分析】根据∠1=60°,∠2=65°,利用三角形内角和定理求出∠ABC的度数,然后可得AB>BC>AC,由切线长定理得AC=CD,BC=CE,利用等量代换求得AB>CE>CD即可.
【解答】解:∵∠1=60°,∠2=65°,
∴∠ABC=180°﹣∠1﹣∠2=180°﹣60°﹣65°=55°,
∴∠2>∠1>∠ABC,
∴AB>BC>AC,
∵CA,CD分别切圆O1于A,D两点,CB、CE分别切圆O2于B,E两点,
∴AC=CD,BC=CE,
∴AB>CE>CD.
故选:A.
【点评】此题主要考查切线长定理和三角形三边关系,三角形内角和定理等知识点,解答此题的关键是利用三角形内角和定理求出∠ABC的度数.
7.如图,在△ABC中,点D是△ABC的内心,连接DB,DC,过点D作EF∥BC分别交AB、AC于点E、F,若BE+CF=8,则EF的长度为( )
A.4
B.5
C.8
D.16
【分析】根据点D是△ABC的内心:在三角形中,三个内角的三个角平分线相交于一点,这个点叫做三角形的内心.可得BD平分∠ABC,CD平分∠ACB,再根据EF∥BC,可得∠EDB=∠EBD,∠FDC=∠FCD,得ED=EB,FD=FC,根据BE+CF=8进而得EF的长度.
【解答】解:∵点D是△ABC的内心,
∴BD平分∠ABC,CD平分∠ACB,
∴∠EBD=∠DBC,∠FCD=∠DCB,
∵EF∥BC,
∴∠EDB=∠DBC,∠FDC=∠DCB,
∴∠EDB=∠EBD,∠FDC=∠FCD,
∴ED=EB,FD=FC,
∴EF=ED+FD=BE+CF=8.
答:EF的长度为8.
故选:C.
【点评】本题考查了三角形的内切圆与内心、平行线的性质,解决本题的关键是掌握三角形的内心.
8.如图,在△ABC中,AC=6,BC=8,AB=10,O是△ABC的内心,作OD⊥AB于D,则AD的长为( )
A.2
B.4
C.5
D.6
【分析】设⊙O与△ABC各边分别相切于D、E、F,如图,连接OD、OE、OF,利用切线的性质得OD⊥AB,OE⊥AC,OF⊥BC,利用勾股定理的逆定理可判断△ABC为直角三角形,再利用四边形OECF为正方形,设CE=r,则CF=r,AD=AE=6﹣r,BF=BD=8﹣r,则6﹣r+8﹣r=10,然后求出r,从而得到AD的长.
【解答】解:设⊙O与△ABC各边分别相切于D、E、F,如图,
连接OD、OE、OF,
则OD⊥AB,OE⊥AC,OF⊥BC,
∵AC=6,BC=8,AB=10,
∴AC2+BC2=AB2,
∴△ABC为直角三角形,
易得四边形OECF为正方形,设CE=r,则CF=r,AD=AE=6﹣r,BF=BD=8﹣r,
∵AD+BD=AB,
∴6﹣r+8﹣r=10,解得r=2,
∴AD=6﹣r=4.
故选:B.
【点评】本题考查了三角形内心的性质:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.
9.如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC等于( )
A.125°
B.120°
C.115°
D.110°
【分析】根据⊙O是△ABC的内切圆,可得OB和OC是△ABC的角平分线,再根据三角形内角和定理进而可得∠BOC的度数.
【解答】解:∵⊙O是△ABC的内切圆,
∴OB和OC是△ABC的角平分线,
∴∠OBC=∠ABC=25°,∠OCB=∠ACB=40°,
∴∠BOC=180°﹣∠OBC﹣∠OCB=115°.
故选:C.
【点评】本题考查了三角形的内切圆与内心,解决本题的关键是掌握三角形的内心定义.
二.填空题(共6小题)
10.如图,在矩形ABCD中,AB=3,BC=4,P是对角线AC上的动点,以点P为圆心,PC长为半径作⊙P.当⊙P与矩形ABCD的边相切时,CP的长为 或 .
【分析】作PE⊥AD于E,PF⊥AB于F,根据勾股定理求出AC,分⊙P与AD相切、⊙P与AB相切相切两种情况,根据相似三角形的判定定理和性质定理计算.
【解答】解:作PE⊥AD于E,PF⊥AB于F,
在Rt△ABC中,AC==5,
由题意可知,⊙P只能与矩形ABCD的边AD、AB相切,
当⊙P与AD相切时,PE=PC,
∵PE⊥AD,CD⊥AD,
∴PE∥CD,
∴△APE∽△ACD,
∴=,即=,
解得,CP=,
当⊙P与AB相切时,PF=PC,
∵PF⊥AB,CB⊥AB,
∴PF∥BC,
∴△APE∽△ACD,
∴=,即=,
解得,CP=,
综上所述,当⊙P与矩形ABCD的边相切时,CP的长或,
故答案为:或.
【点评】本题考查的是切线的判定和性质、矩形的性质,掌握切线的判定定理、灵活运用分情况讨论思想是解题的关键.
11.直线l经过点A
(4,0),B(0,2),若⊙M的半径为1,圆心M在x轴上,当⊙M与直线l相切时,则点M的坐标 (4﹣,0)或(4+,0) .
【分析】根据勾股定理得到AB==2,设M坐标为(m,0)(m>0),即OM=m,若M′在A点左侧时,AM′=4﹣m,若M在A点右侧时,AM=m﹣4,根据相似三角形的判定和性质定理即可得到结论.
【解答】解:∵直线l经过点A(4,0),B(0,2),
∴AB==2,
设M坐标为(m,0)(m>0),即OM=m,
若M′在A点左侧时,AM′=4﹣m,
当AB是⊙O的切线,
∴∠M′C′A=90°,
∵∠M′AC′=∠BAO,∠M′C′A=∠BOA=90°,
∴△M′AC′∽△BAO,
∴=,即=,
解得:m=4﹣,此时M′(4﹣,0);
若M在A点右侧时,AM=m﹣4,
同理△AMN∽△BAO,则有=,即=,
解得:m=4+.此时M(4+,0),
综上所述,M(4﹣,0)或(4+,0),
故答案为:M(4﹣,0)或(4+,0),
【点评】本题考查了切线的判定和性质,解答本题的关键是画出示意图,熟练掌握切线的性质及锐角三角函数的定义,难度一般.
12.一个菱形的周长是20cm,两对角线之比是4:3,则该菱形的内切圆的半径是 cm.
【分析】直接利用菱形的性质结合直角三角形的性质得出答案.
【解答】解:如图所示:菱形ABCD,对角线AC,BD,可得菱形内切圆的圆心即为对角线交点,
设AB与圆相切于点E,可得OE⊥AB,
∵一个菱形的周长是20cm,两对角线之比是4:3,
∴AB=5cm,
设BO=4x,则AO=3x,
故(4x)2+(3x)2=25,
解得:x=1,
则AO=3,BO=4,
故EO?AB=AO?BO,
解得:EO=.
故答案为:.
【点评】此题主要考查了菱形的性质,正确画出图形得出菱形对角线的长是解题关键.
13.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=15,则四边形ABCD的周长为 50 .
【分析】根据切线长定理得到AE=AH,BE=BF,CF=CG,DH=DG,得到AD+BC=AB+CD=25,根据四边形的周长公式计算,得到答案.
【解答】解:∵四边形ABCD是⊙O的外切四边形,
∴AE=AH,BE=BF,CF=CG,DH=DG,
∴AD+BC=AB+CD=25,
∴四边形ABCD的周长=AD+BC+AB+CD=25+25=50,
故答案为:50.
【点评】本题考查的是切线长定理,掌握从圆外一点引圆的两条切线,它们的切线长相等是解题的关键.
14.如图,在△ABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆半径r= 1 .
【分析】在△ABC中,∠C=90°,AC=3,BC=4,根据勾股定理可得AB=5,设△ABC的内切圆与三条边的切点分别为D、E、F,连接OD、OE、OF,可得OD⊥AB,OE⊥BC,OF⊥AC,可得矩形EOFC,再根据切线长定理可得CE=CF,所以矩形EOFC是正方形,可得CE=CF=r,所以AF=AD=3﹣r,BE=BD=4﹣r,进而可得△ABC的内切圆半径r的值.
【解答】解:在△ABC中,∠C=90°,AC=3,BC=4,
根据勾股定理,得AB=5,
如图,设△ABC的内切圆与三条边的切点分别为D、E、F,
连接OD、OE、OF,
∴OD⊥AB,OE⊥BC,OF⊥AC,
∵∠C=90°,
∴四边形EOFC是矩形,
根据切线长定理,得
CE=CF,
∴矩形EOFC是正方形,
∴CE=CF=r,
∴AF=AD=AC﹣FC=3﹣r,
BE=BD=BC﹣CE=4﹣r,
∵AD+BD=AB,
∴3﹣r+4﹣r=5,
解得r=1.
则△ABC的内切圆半径r=1.
故答案为:1.
【点评】本题考查了三角形的内切圆与内心,解决本题的关键是掌握三角形的内切圆与内心.
15.如图,△ABC为锐角三角形,I为内心,O为外心,若OI⊥AI,AB=4,则BE= 2 .
【分析】由点I是△ABC的内心,可证明∠BIE=∠DBI,可得BD=ID,由OI⊥AI,可得AI=ID=BD,证明△BDE∽△ADB,得,即可得出AB=2.
【解答】解:作△ABC的外接圆,延长AE交⊙O于点D,连接DB,CD,BI,
∵点I是△ABC的内心,
∴∠ABI=∠IBE,∠BAE=∠EAC,
∵∠DAC=∠DBC,
∴∠BIE=∠BAI+∠ABI,∠DBI=∠EBD+∠IBE,
∴∠BIE=∠DBI,
∴BD=ID,
∵OI⊥AI,
∴AI=ID=BD,
∵∠EBD=∠DAC=∠BAD,∠BDE=∠ADB,
∴△BDE∽△ADB,
∴,
∵AB=4,
∴BE=2,
故答案为:2.
【点评】本题考查三角形的内心和外心的概念,相似三角形的判定和性质,垂径定理.解题的关键是正确理解三角形内心是三角形三条角平分线的交点.
三.解答题(共3小题)
16.如图,AB是⊙O直径,AC是⊙O切线,BC交⊙O与点E.
(1)若点D在AC上,连接DE,且AD=DE,求证:DE是⊙O的切线;
(2)若CE=1.BE=3,求∠ACB的度数.
【分析】(1)连接OE,AE,根据切线的性质与判定即可求出答案.
(2)易证△CAE∽△ABE,所以AE2=CE?BE,求出AE=,根据锐角三角函数的定义即可求出答案.
【解答】解:(1)连接OE,AE,
∵AE=DE,OA=OE,
∴∠DAE=∠DEA,∠OAE=∠OEA,
∵AC是⊙O的切线,
∴∠BAC=90°,
∴∠DAE+∠OAE=∠DEA+∠OEA=90°,
∵OE是⊙O的半径,
∴DE是⊙O的切线.
(2)∵AB是⊙O的直径,
∴∠AEB=90°,
∵∠C+∠CAE=∠CAE+∠BAE=90°,
∴∠C=∠BAE,
∴△CAE∽△ABE,
∴AE2=CE?BE,
∴AE2=1×3,
∴AE=,
在Rt△ACE中,
∴tan∠ACE==,
∴∠ACE=60°.
【点评】本题考查圆的综合问题,解题的关键是熟练运用切线的判定与性质,相似三角形的性质与判定,本题属于中等题型.
17.如图,点B在⊙O外,以B点为圆心,OB长为半径画弧与⊙O相交于两点C,D,与直线OB相交A点.当AC=5时,求AD的长.
【分析】连接OC、OD.根据切线的判定方法证明AC、AD都是圆的切线,再根据切线长定理即可求解.
【解答】解:连接OC、OD.
∵OA是⊙B的直径,
∴∠OCA=∠ODA=90°,
∴AC、AD都是⊙O的切线.
∴AD=AC=5.
【点评】此题综合运用了圆周角定理的推论、切线的判定定理和切线长定理.
18.如图.已知△ABC的周长为2p,在AB、AC上分别取点M和N,使MN∥BC,且MN与△ABC的内切圆相切.求MN的最大值.
【分析】设BC=a,BC边上的高为h,内切圆半径为r.则S△ABC=pr,从而得出MN是p的二次函数,再求最大值.
【解答】解:设BC=a,BC边上的高为h,
内切圆半径为r.
∵△AMN∽△ABC,
∴,
MN=a(1),
∵S△ABC=ar+br+cr=(a+b+c)r=?2pr=pr,
∴r==,
∴MN=a(1﹣)=(1﹣)≤p?=,
当且仅当,
即a=时,取等号,
∴MN的最大值为.
【点评】本题查了三角形的内切圆、二次函数的最值和相似三角形的判定和性质.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/9
9:09:30;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
24.2.2
直线和圆的位置关系(2)
一.选择题(共9小题)
1.如图,在矩形ABCD中,BC=8,以AB为直径作⊙O,将矩形ABCD绕点B旋转,使所得矩形A'BC'D'的边C'D'与⊙O相切,切点为E,边A'B与⊙O相交于点F.若BF=8,则CD长为( )
A.9
B.10
C.8
D.12
2.如图,在直线l上有相距7cm的两点A和O(点A在点O的右侧),以O为圆心作半径为1cm的圆,过点A作直线AB⊥l.将⊙O以2cm/s的速度向右移动(点O始终在直线l上),则⊙O与直线AB在( )秒时相切.
A.3
B.3.5
C.3或4
D.3或3.5
3.已知圆O的半径为R,点O到直线m的距离为d、R、d是方程x2﹣4x+a=0的两根,当直线m与圆O相切时,a的值是( )
A.3
B.4
C.5
D.无法确定
4.如图,是用一把直尺、含60°角的直角三角板和光盘摆放而成,点A为60°角与直尺交点,点B为光盘与直尺唯一交点,若AB=3,则光盘的直径是( )
A.6
B.3
C.6
D.3
5.如图,P为圆O外一点,PA,PB分别切圆O于A,B两点,若PA=3,则PB=( )
A.2
B.3
C.4
D.5
6.如图中,CA,CD分别切圆O1于A,D两点,CB、CE分别切圆O2于B,E两点.若∠1=60°,∠2=65°,判断AB、CD、CE的长度,下列关系何者正确( )
A.AB>CE>CD
B.AB=CE>CD
C.AB>CD>CE
D.AB=CD=CE
7.如图,在△ABC中,点D是△ABC的内心,连接DB,DC,过点D作EF∥BC分别交AB、AC于点E、F,若BE+CF=8,则EF的长度为( )
A.4
B.5
C.8
D.16
8.如图,在△ABC中,AC=6,BC=8,AB=10,O是△ABC的内心,作OD⊥AB于D,则AD的长为( )
A.2
B.4
C.5
D.6
9.如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC等于( )
A.125°
B.120°
C.115°
D.110°
二.填空题(共6小题)
10.如图,在矩形ABCD中,AB=3,BC=4,P是对角线AC上的动点,以点P为圆心,PC长为半径作⊙P.当⊙P与矩形ABCD的边相切时,CP的长为
.
11.直线l经过点A
(4,0),B(0,2),若⊙M的半径为1,圆心M在x轴上,当⊙M与直线l相切时,则点M的坐标
.
12.一个菱形的周长是20cm,两对角线之比是4:3,则该菱形的内切圆的半径是
cm.
13.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=15,则四边形ABCD的周长为
.
14.如图,在△ABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆半径r=
.
15.如图,△ABC为锐角三角形,I为内心,O为外心,若OI⊥AI,AB=4,则BE=
.
三.解答题(共3小题)
16.如图,AB是⊙O直径,AC是⊙O切线,BC交⊙O与点E.
(1)若点D在AC上,连接DE,且AD=DE,求证:DE是⊙O的切线;
(2)若CE=1.BE=3,求∠ACB的度数.
17.如图,点B在⊙O外,以B点为圆心,OB长为半径画弧与⊙O相交于两点C,D,与直线OB相交A点.当AC=5时,求AD的长.
18.如图.已知△ABC的周长为2p,在AB、AC上分别取点M和N,使MN∥BC,且MN与△ABC的内切圆相切.求MN的最大值.
24.2.2
直线和圆的位置关系(2)
参考答案与试题解析
一.选择题(共9小题)
1.如图,在矩形ABCD中,BC=8,以AB为直径作⊙O,将矩形ABCD绕点B旋转,使所得矩形A'BC'D'的边C'D'与⊙O相切,切点为E,边A'B与⊙O相交于点F.若BF=8,则CD长为( )
A.9
B.10
C.8
D.12
【分析】连接OE,延长EO交BF于点M,设OB=OE=x,则OM=8﹣x,由勾股定理得出(8﹣x)2+42=x2,解得x=5,则得出答案.
【解答】解:连接OE,延长EO交BF于点M,
∵C'D'与⊙O相切,
∴∠OEC′=90°,
又矩形A'BC'D'中,A'B∥C'D',
∴∠EMB=90°,
∴BM=FM,
∵矩形ABCD绕点B旋转所得矩形为A′BC′D′,
∴∠C′=∠C=90°,AB=CD,BC=B′C=8,
∴四边形EMBC'为矩形,
∴ME=8,
设OB=OE=x,则OM=8﹣x,
∵OM2+BM2=OB2,
∴(8﹣x)2+42=x2,
解得x=5,
∴AB=CD=10.
故选:B.
【点评】本题主要考查圆的切线的判定与性质,解题的关键是掌握矩形的判定与性质、旋转的性质、切线的性质、垂径定理等知识点.
2.如图,在直线l上有相距7cm的两点A和O(点A在点O的右侧),以O为圆心作半径为1cm的圆,过点A作直线AB⊥l.将⊙O以2cm/s的速度向右移动(点O始终在直线l上),则⊙O与直线AB在( )秒时相切.
A.3
B.3.5
C.3或4
D.3或3.5
【分析】根据切线的判定方法,当点O到AB的距离为1cm时,⊙O与AB相切,然后计算出圆向右移动的距离,然后计算出对应的时间.
【解答】解:当点O到AB的距离为1cm时,⊙O与AB相切,
∵开始时O点到AB的距离为7,
∴当圆向右移动7﹣1或7+1时,点O到AB的距离为1cm,此时⊙O与AB相切,
∴t==3(s)或t==4(s),
即⊙O与直线AB在3秒或4秒时相切.
故选:C.
【点评】本题考查了切线的判定与性质:圆的切线垂直于经过切点的半径;经过半径的外端且垂直于这条半径的直线是圆的切线,当圆心到直线的距离等于圆的半径,则直线与圆相切.
3.已知圆O的半径为R,点O到直线m的距离为d、R、d是方程x2﹣4x+a=0的两根,当直线m与圆O相切时,a的值是( )
A.3
B.4
C.5
D.无法确定
【分析】若直线和圆相切,则d=R.即方程有两个相等的实数根,得16﹣4a=0,可得a=4.
【解答】解:∵直线和圆相切,
∴d=R,
∴△=16﹣4a=0,
∴a=4,
故选:B.
【点评】此题考查了直线和圆的位置关系与数量关系之间的联系,关键是熟练运用根的判别式判断方程的根的情况.
4.如图,是用一把直尺、含60°角的直角三角板和光盘摆放而成,点A为60°角与直尺交点,点B为光盘与直尺唯一交点,若AB=3,则光盘的直径是( )
A.6
B.3
C.6
D.3
【分析】设三角板与圆的切点为C,连接OA、OB,由切线长定理得出AB=AC=3、∠OAB=60°,根据OB=ABtan∠OAB可得答案.
【解答】解:设三角板与圆的切点为C,连接OA、OB,
由切线长定理知AB=AC=3,OA平分∠BAC,
∴∠OAB=60°,
在Rt△ABO中,OB=ABtan∠OAB=3,
∴光盘的直径为6,
故选:A.
【点评】本题主要考查切线的性质,解题的关键是掌握切线长定理和解直角三角形的应用.
5.如图,P为圆O外一点,PA,PB分别切圆O于A,B两点,若PA=3,则PB=( )
A.2
B.3
C.4
D.5
【分析】连接OA、OB、OP,根据切线的性质得出OA⊥PA,OB⊥PB,即可求得PB=PA=3.
【解答】解:连接OA,OB,OP,
∵PA,PB分别切圆O于A,B两点,
∴OA⊥PA,OB⊥PB,
∴PB=PA=3,
故选:B.
【点评】本题考查了切线长定理,三角形全等的判定和性质,作出辅助线根据全等三角形是解题的关键.
6.如图中,CA,CD分别切圆O1于A,D两点,CB、CE分别切圆O2于B,E两点.若∠1=60°,∠2=65°,判断AB、CD、CE的长度,下列关系何者正确( )
A.AB>CE>CD
B.AB=CE>CD
C.AB>CD>CE
D.AB=CD=CE
【分析】根据∠1=60°,∠2=65°,利用三角形内角和定理求出∠ABC的度数,然后可得AB>BC>AC,由切线长定理得AC=CD,BC=CE,利用等量代换求得AB>CE>CD即可.
【解答】解:∵∠1=60°,∠2=65°,
∴∠ABC=180°﹣∠1﹣∠2=180°﹣60°﹣65°=55°,
∴∠2>∠1>∠ABC,
∴AB>BC>AC,
∵CA,CD分别切圆O1于A,D两点,CB、CE分别切圆O2于B,E两点,
∴AC=CD,BC=CE,
∴AB>CE>CD.
故选:A.
【点评】此题主要考查切线长定理和三角形三边关系,三角形内角和定理等知识点,解答此题的关键是利用三角形内角和定理求出∠ABC的度数.
7.如图,在△ABC中,点D是△ABC的内心,连接DB,DC,过点D作EF∥BC分别交AB、AC于点E、F,若BE+CF=8,则EF的长度为( )
A.4
B.5
C.8
D.16
【分析】根据点D是△ABC的内心:在三角形中,三个内角的三个角平分线相交于一点,这个点叫做三角形的内心.可得BD平分∠ABC,CD平分∠ACB,再根据EF∥BC,可得∠EDB=∠EBD,∠FDC=∠FCD,得ED=EB,FD=FC,根据BE+CF=8进而得EF的长度.
【解答】解:∵点D是△ABC的内心,
∴BD平分∠ABC,CD平分∠ACB,
∴∠EBD=∠DBC,∠FCD=∠DCB,
∵EF∥BC,
∴∠EDB=∠DBC,∠FDC=∠DCB,
∴∠EDB=∠EBD,∠FDC=∠FCD,
∴ED=EB,FD=FC,
∴EF=ED+FD=BE+CF=8.
答:EF的长度为8.
故选:C.
【点评】本题考查了三角形的内切圆与内心、平行线的性质,解决本题的关键是掌握三角形的内心.
8.如图,在△ABC中,AC=6,BC=8,AB=10,O是△ABC的内心,作OD⊥AB于D,则AD的长为( )
A.2
B.4
C.5
D.6
【分析】设⊙O与△ABC各边分别相切于D、E、F,如图,连接OD、OE、OF,利用切线的性质得OD⊥AB,OE⊥AC,OF⊥BC,利用勾股定理的逆定理可判断△ABC为直角三角形,再利用四边形OECF为正方形,设CE=r,则CF=r,AD=AE=6﹣r,BF=BD=8﹣r,则6﹣r+8﹣r=10,然后求出r,从而得到AD的长.
【解答】解:设⊙O与△ABC各边分别相切于D、E、F,如图,
连接OD、OE、OF,
则OD⊥AB,OE⊥AC,OF⊥BC,
∵AC=6,BC=8,AB=10,
∴AC2+BC2=AB2,
∴△ABC为直角三角形,
易得四边形OECF为正方形,设CE=r,则CF=r,AD=AE=6﹣r,BF=BD=8﹣r,
∵AD+BD=AB,
∴6﹣r+8﹣r=10,解得r=2,
∴AD=6﹣r=4.
故选:B.
【点评】本题考查了三角形内心的性质:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.
9.如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC等于( )
A.125°
B.120°
C.115°
D.110°
【分析】根据⊙O是△ABC的内切圆,可得OB和OC是△ABC的角平分线,再根据三角形内角和定理进而可得∠BOC的度数.
【解答】解:∵⊙O是△ABC的内切圆,
∴OB和OC是△ABC的角平分线,
∴∠OBC=∠ABC=25°,∠OCB=∠ACB=40°,
∴∠BOC=180°﹣∠OBC﹣∠OCB=115°.
故选:C.
【点评】本题考查了三角形的内切圆与内心,解决本题的关键是掌握三角形的内心定义.
二.填空题(共6小题)
10.如图,在矩形ABCD中,AB=3,BC=4,P是对角线AC上的动点,以点P为圆心,PC长为半径作⊙P.当⊙P与矩形ABCD的边相切时,CP的长为 或 .
【分析】作PE⊥AD于E,PF⊥AB于F,根据勾股定理求出AC,分⊙P与AD相切、⊙P与AB相切相切两种情况,根据相似三角形的判定定理和性质定理计算.
【解答】解:作PE⊥AD于E,PF⊥AB于F,
在Rt△ABC中,AC==5,
由题意可知,⊙P只能与矩形ABCD的边AD、AB相切,
当⊙P与AD相切时,PE=PC,
∵PE⊥AD,CD⊥AD,
∴PE∥CD,
∴△APE∽△ACD,
∴=,即=,
解得,CP=,
当⊙P与AB相切时,PF=PC,
∵PF⊥AB,CB⊥AB,
∴PF∥BC,
∴△APE∽△ACD,
∴=,即=,
解得,CP=,
综上所述,当⊙P与矩形ABCD的边相切时,CP的长或,
故答案为:或.
【点评】本题考查的是切线的判定和性质、矩形的性质,掌握切线的判定定理、灵活运用分情况讨论思想是解题的关键.
11.直线l经过点A
(4,0),B(0,2),若⊙M的半径为1,圆心M在x轴上,当⊙M与直线l相切时,则点M的坐标 (4﹣,0)或(4+,0) .
【分析】根据勾股定理得到AB==2,设M坐标为(m,0)(m>0),即OM=m,若M′在A点左侧时,AM′=4﹣m,若M在A点右侧时,AM=m﹣4,根据相似三角形的判定和性质定理即可得到结论.
【解答】解:∵直线l经过点A(4,0),B(0,2),
∴AB==2,
设M坐标为(m,0)(m>0),即OM=m,
若M′在A点左侧时,AM′=4﹣m,
当AB是⊙O的切线,
∴∠M′C′A=90°,
∵∠M′AC′=∠BAO,∠M′C′A=∠BOA=90°,
∴△M′AC′∽△BAO,
∴=,即=,
解得:m=4﹣,此时M′(4﹣,0);
若M在A点右侧时,AM=m﹣4,
同理△AMN∽△BAO,则有=,即=,
解得:m=4+.此时M(4+,0),
综上所述,M(4﹣,0)或(4+,0),
故答案为:M(4﹣,0)或(4+,0),
【点评】本题考查了切线的判定和性质,解答本题的关键是画出示意图,熟练掌握切线的性质及锐角三角函数的定义,难度一般.
12.一个菱形的周长是20cm,两对角线之比是4:3,则该菱形的内切圆的半径是 cm.
【分析】直接利用菱形的性质结合直角三角形的性质得出答案.
【解答】解:如图所示:菱形ABCD,对角线AC,BD,可得菱形内切圆的圆心即为对角线交点,
设AB与圆相切于点E,可得OE⊥AB,
∵一个菱形的周长是20cm,两对角线之比是4:3,
∴AB=5cm,
设BO=4x,则AO=3x,
故(4x)2+(3x)2=25,
解得:x=1,
则AO=3,BO=4,
故EO?AB=AO?BO,
解得:EO=.
故答案为:.
【点评】此题主要考查了菱形的性质,正确画出图形得出菱形对角线的长是解题关键.
13.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=15,则四边形ABCD的周长为 50 .
【分析】根据切线长定理得到AE=AH,BE=BF,CF=CG,DH=DG,得到AD+BC=AB+CD=25,根据四边形的周长公式计算,得到答案.
【解答】解:∵四边形ABCD是⊙O的外切四边形,
∴AE=AH,BE=BF,CF=CG,DH=DG,
∴AD+BC=AB+CD=25,
∴四边形ABCD的周长=AD+BC+AB+CD=25+25=50,
故答案为:50.
【点评】本题考查的是切线长定理,掌握从圆外一点引圆的两条切线,它们的切线长相等是解题的关键.
14.如图,在△ABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆半径r= 1 .
【分析】在△ABC中,∠C=90°,AC=3,BC=4,根据勾股定理可得AB=5,设△ABC的内切圆与三条边的切点分别为D、E、F,连接OD、OE、OF,可得OD⊥AB,OE⊥BC,OF⊥AC,可得矩形EOFC,再根据切线长定理可得CE=CF,所以矩形EOFC是正方形,可得CE=CF=r,所以AF=AD=3﹣r,BE=BD=4﹣r,进而可得△ABC的内切圆半径r的值.
【解答】解:在△ABC中,∠C=90°,AC=3,BC=4,
根据勾股定理,得AB=5,
如图,设△ABC的内切圆与三条边的切点分别为D、E、F,
连接OD、OE、OF,
∴OD⊥AB,OE⊥BC,OF⊥AC,
∵∠C=90°,
∴四边形EOFC是矩形,
根据切线长定理,得
CE=CF,
∴矩形EOFC是正方形,
∴CE=CF=r,
∴AF=AD=AC﹣FC=3﹣r,
BE=BD=BC﹣CE=4﹣r,
∵AD+BD=AB,
∴3﹣r+4﹣r=5,
解得r=1.
则△ABC的内切圆半径r=1.
故答案为:1.
【点评】本题考查了三角形的内切圆与内心,解决本题的关键是掌握三角形的内切圆与内心.
15.如图,△ABC为锐角三角形,I为内心,O为外心,若OI⊥AI,AB=4,则BE= 2 .
【分析】由点I是△ABC的内心,可证明∠BIE=∠DBI,可得BD=ID,由OI⊥AI,可得AI=ID=BD,证明△BDE∽△ADB,得,即可得出AB=2.
【解答】解:作△ABC的外接圆,延长AE交⊙O于点D,连接DB,CD,BI,
∵点I是△ABC的内心,
∴∠ABI=∠IBE,∠BAE=∠EAC,
∵∠DAC=∠DBC,
∴∠BIE=∠BAI+∠ABI,∠DBI=∠EBD+∠IBE,
∴∠BIE=∠DBI,
∴BD=ID,
∵OI⊥AI,
∴AI=ID=BD,
∵∠EBD=∠DAC=∠BAD,∠BDE=∠ADB,
∴△BDE∽△ADB,
∴,
∵AB=4,
∴BE=2,
故答案为:2.
【点评】本题考查三角形的内心和外心的概念,相似三角形的判定和性质,垂径定理.解题的关键是正确理解三角形内心是三角形三条角平分线的交点.
三.解答题(共3小题)
16.如图,AB是⊙O直径,AC是⊙O切线,BC交⊙O与点E.
(1)若点D在AC上,连接DE,且AD=DE,求证:DE是⊙O的切线;
(2)若CE=1.BE=3,求∠ACB的度数.
【分析】(1)连接OE,AE,根据切线的性质与判定即可求出答案.
(2)易证△CAE∽△ABE,所以AE2=CE?BE,求出AE=,根据锐角三角函数的定义即可求出答案.
【解答】解:(1)连接OE,AE,
∵AE=DE,OA=OE,
∴∠DAE=∠DEA,∠OAE=∠OEA,
∵AC是⊙O的切线,
∴∠BAC=90°,
∴∠DAE+∠OAE=∠DEA+∠OEA=90°,
∵OE是⊙O的半径,
∴DE是⊙O的切线.
(2)∵AB是⊙O的直径,
∴∠AEB=90°,
∵∠C+∠CAE=∠CAE+∠BAE=90°,
∴∠C=∠BAE,
∴△CAE∽△ABE,
∴AE2=CE?BE,
∴AE2=1×3,
∴AE=,
在Rt△ACE中,
∴tan∠ACE==,
∴∠ACE=60°.
【点评】本题考查圆的综合问题,解题的关键是熟练运用切线的判定与性质,相似三角形的性质与判定,本题属于中等题型.
17.如图,点B在⊙O外,以B点为圆心,OB长为半径画弧与⊙O相交于两点C,D,与直线OB相交A点.当AC=5时,求AD的长.
【分析】连接OC、OD.根据切线的判定方法证明AC、AD都是圆的切线,再根据切线长定理即可求解.
【解答】解:连接OC、OD.
∵OA是⊙B的直径,
∴∠OCA=∠ODA=90°,
∴AC、AD都是⊙O的切线.
∴AD=AC=5.
【点评】此题综合运用了圆周角定理的推论、切线的判定定理和切线长定理.
18.如图.已知△ABC的周长为2p,在AB、AC上分别取点M和N,使MN∥BC,且MN与△ABC的内切圆相切.求MN的最大值.
【分析】设BC=a,BC边上的高为h,内切圆半径为r.则S△ABC=pr,从而得出MN是p的二次函数,再求最大值.
【解答】解:设BC=a,BC边上的高为h,
内切圆半径为r.
∵△AMN∽△ABC,
∴,
MN=a(1),
∵S△ABC=ar+br+cr=(a+b+c)r=?2pr=pr,
∴r==,
∴MN=a(1﹣)=(1﹣)≤p?=,
当且仅当,
即a=时,取等号,
∴MN的最大值为.
【点评】本题查了三角形的内切圆、二次函数的最值和相似三角形的判定和性质.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/9
9:09:30;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
同课章节目录
