24.1.2 圆的有关性质同步练习(含解析)
文档属性
| 名称 | 24.1.2 圆的有关性质同步练习(含解析) |  | |
| 格式 | rar | ||
| 文件大小 | 565.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 21:05:36 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
24.1
圆的有关性质(2)
一.选择题(共9小题)
1.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是( )
A.
B.3
C.3
D.4
2.如图,将大小不同的两块量角器的零度线对齐,且小量角器的中心O2,恰好在大量角器的圆周上,设图中两圆周的交点为P,且点P在小量角器上对应的刻度为63°,那么点P在大量角器上对应的刻度为(只考虑小于90°的角)( )
A.54°
B.55°
C.56°
D.57°
3.如图,圆O通过五边形OABCD的四个顶点.若=150°,∠A=75°,∠D=60°,则的度数为何?( )
A.25°
B.40°
C.50°
D.60°
4.如图,在⊙O中,直径AB⊥CD,∠A=26°,则∠D度数是( )
A.26°
B.38°
C.52°
D.64°
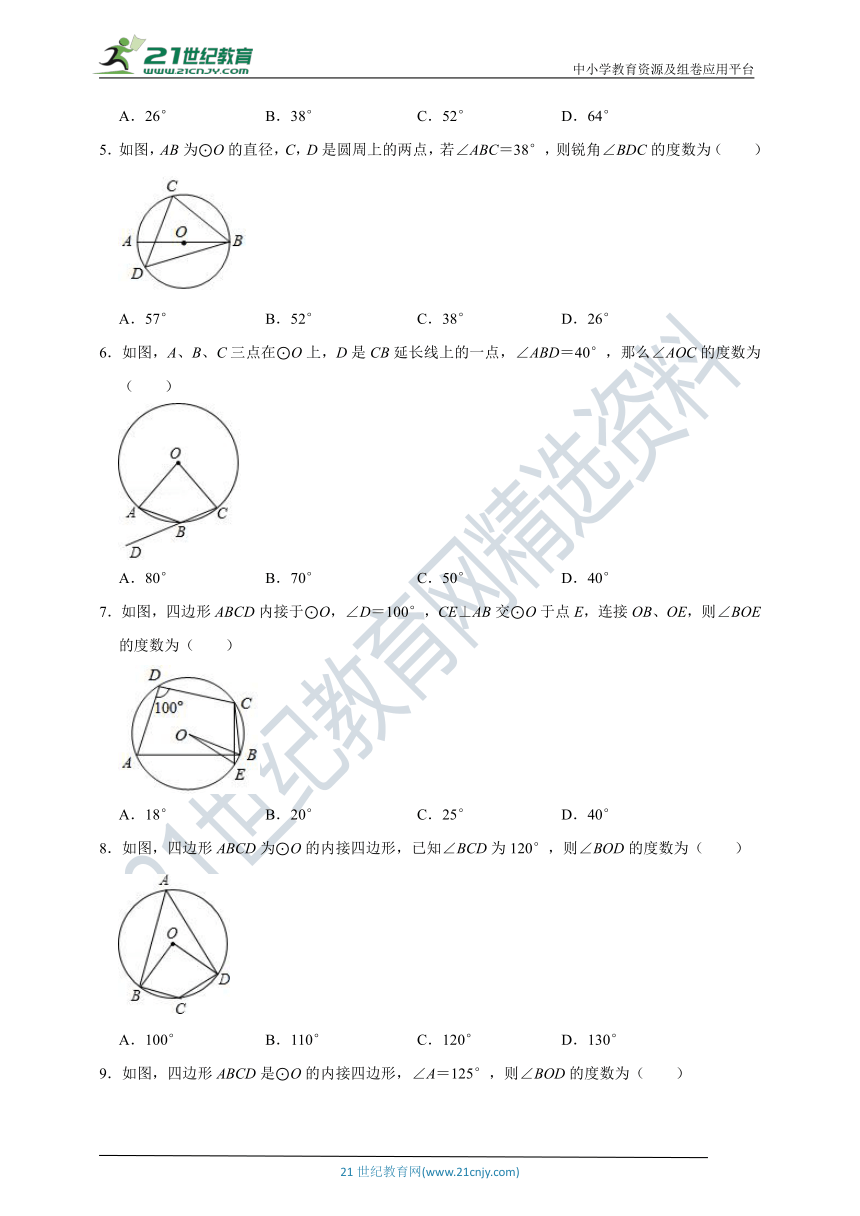
5.如图,AB为⊙O的直径,C,D是圆周上的两点,若∠ABC=38°,则锐角∠BDC的度数为( )
A.57°
B.52°
C.38°
D.26°
6.如图,A、B、C三点在⊙O上,D是CB延长线上的一点,∠ABD=40°,那么∠AOC的度数为( )
A.80°
B.70°
C.50°
D.40°
7.如图,四边形ABCD内接于⊙O,∠D=100°,CE⊥AB交⊙O于点E,连接OB、OE,则∠BOE的度数为( )
A.18°
B.20°
C.25°
D.40°
8.如图,四边形ABCD为⊙O的内接四边形,已知∠BCD为120°,则∠BOD的度数为( )
A.100°
B.110°
C.120°
D.130°
9.如图,四边形ABCD是⊙O的内接四边形,∠A=125°,则∠BOD的度数为( )
A.55°
B.65°
C.110°
D.125°
二.填空题(共6小题)
10.如图,扇形OAB中,∠AOB=60°,OA=4,点C为弧AB的中点,D为半径OA上一点,点A关于直线CD的对称点为E,若点E落在半径OA上,则OE=
.
11.长度等于6的弦所对的圆心角是90°,则该圆半径为
.
12.如图,⊙O为锐角ABC的外接圆,若∠BAO=15°,则∠C的度数为
.
13.如图,AB为⊙O的直径,C,D为⊙O上的点,=.若∠CAB=50°,则∠CAD=
°.
14.如图,点O为线段BC的中点,点A、C、D到点O的距离相等,若∠ABC=50°,则∠ADC的度数是
°.
15.如图,四边形ABCD内接于⊙O,且四边形OABC是平行四边形,则∠D=
.
三.解答题(共3小题)
16.如图,在⊙O中,=,CD⊥OA于点D,CE⊥OB于点E.
(1)求证:CD=CE;
(2)若∠AOB=120°,OA=2,求四边形DOEC的面积.
17.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,延长CA交⊙O于点E.连结ED交AB于点F.
(1)求证:△CDE是等腰三角形.
(2)当CD:AC=2:时,求的值.
18.(1)解方程:x2﹣2x﹣24=0.
(2)如图,A,B,C,D四点都在⊙O上,BD为直径,四边形OABC是平行四边形,求∠D的度数.
24.1
圆的有关性质(2)
参考答案与试题解析
一.选择题(共9小题)
1.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是( )
A.
B.3
C.3
D.4
【分析】连接OD,交AC于F,根据垂径定理得出OD⊥AC,AF=CF,进而证得DF=BC,根据三角形中位线定理求得OF=BC=DF,从而求得BC=DF=2,利用勾股定理即可求得AC.
【解答】解:连接OD,交AC于F,
∵D是的中点,
∴OD⊥AC,AF=CF,
∴∠DFE=90°,
∵OA=OB,AF=CF,
∴OF=BC,
∵AB是直径,
∴∠ACB=90°,
在△EFD和△ECB中
∴△EFD≌△ECB(AAS),
∴DF=BC,
∴OF=DF,
∵OD=3,
∴OF=1,
∴BC=2,
在Rt△ABC中,AC2=AB2﹣BC2,
∴AC===4,
故选:D.
【点评】本题考查了垂径定理,三角形全等的判定和性质,三角形中位线定理,熟练掌握性质定理是解题的关键.
2.如图,将大小不同的两块量角器的零度线对齐,且小量角器的中心O2,恰好在大量角器的圆周上,设图中两圆周的交点为P,且点P在小量角器上对应的刻度为63°,那么点P在大量角器上对应的刻度为(只考虑小于90°的角)( )
A.54°
B.55°
C.56°
D.57°
【分析】连接O1P,O2P,如图,先根据O1P=O2P得到∠O1PO2=∠O1O2P=63°,然后根据三角形内角和求出∠PO1O2即可.
【解答】解:连接O1P,O2P,如图,
∵P在小量角器上对应的刻度为63°,
即∠O1O2P=63°,
而O1P=O2P,
∴∠O1PO2=∠O1O2P=63°,
∴∠PO1O2=180°﹣63°﹣63°=54°,
即点P在大量角器上对应的刻度为54°(只考虑小于90°的角).
故选:A.
【点评】本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
3.如图,圆O通过五边形OABCD的四个顶点.若=150°,∠A=75°,∠D=60°,则的度数为何?( )
A.25°
B.40°
C.50°
D.60°
【分析】连接OB,OC,由半径相等得到△OAB,△OBC,△OCD都为等腰三角形,根据∠A=75°,∠D=60°,求出∠1与∠2的度数,根据的度数确定出∠AOD度数,进而求出∠3的度数,即可确定出的度数.
【解答】解:连接OB、OC,
∵OA=OB=OC=OD,
∴△OAB、△OBC、△OCD,皆为等腰三角形,
∵∠A=65°,∠D=60°,
∴∠1=180°﹣2∠A=180°﹣2×75°=30°,∠2=180°﹣2∠D=180°﹣2×60°=60°,
∵=150°,
∴∠AOD=150°,
∴∠3=∠AOD﹣∠1﹣∠2=150°﹣30°﹣60°=60°,
则的度数为60°.
故选:D.
【点评】此题考查了圆心角、弧、弦的关系,多边形内角与外角,弄清圆心角、弧、弦的关系是解本题的关键.
4.如图,在⊙O中,直径AB⊥CD,∠A=26°,则∠D度数是( )
A.26°
B.38°
C.52°
D.64°
【分析】连接OC,如图,先根据圆周角定理得到∠BOC=2∠A=52°,再利用互余计算出∠OCD=38°,然后利用等腰三角形的性质得到∠D的度数.
【解答】解:连接OC,如图,
∵∠A=26°,
∴∠BOC=2∠A=52°,
∵AB⊥CD,
∴∠OCD=90°﹣∠BOC=90°﹣52°=38°,
∵OC=OD,
∴∠D=∠OCD=38°.
故选:B.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
5.如图,AB为⊙O的直径,C,D是圆周上的两点,若∠ABC=38°,则锐角∠BDC的度数为( )
A.57°
B.52°
C.38°
D.26°
【分析】由AB是⊙O的直径,根据直径所对的圆周角是直角,即可得∠ACB=90°,又由∠ABC=38°,即可求得∠A的度数,然后根据在同圆或等圆中,同弧或等弧所对的圆周角相等,即可求得∠BDC的度数.
【解答】解:连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠ABC=38°,
∴∠BAC=90°﹣∠ABC=52°,
∴∠BDC=∠BAC=52°.
故选:B.
【点评】此题考查了圆周角定理.此题难度不大,注意掌握直径所对的圆周角是直角与在同圆或等圆中,同弧或等弧所对的圆周角相等定理的应用是解此题的关键.
6.如图,A、B、C三点在⊙O上,D是CB延长线上的一点,∠ABD=40°,那么∠AOC的度数为( )
A.80°
B.70°
C.50°
D.40°
【分析】作所对的圆周角∠AEC,如图,先利用邻补角计算出∠ABC=140°,再利用圆内接四边形的性质计算出∠E=40°,然后根据圆周角定理得到∠AOC的度数.
【解答】解:所对的圆周角∠AEC,如图,
∵∠ABD=40°,
∴∠ABC=180°﹣40°=140°,
∵∠AEC+∠ABC=180°,
∴∠E=40°,
∴∠AOC=2∠AEC=2×40°=80°.
故选:A.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
7.如图,四边形ABCD内接于⊙O,∠D=100°,CE⊥AB交⊙O于点E,连接OB、OE,则∠BOE的度数为( )
A.18°
B.20°
C.25°
D.40°
【分析】根据圆内接四边形的性质和圆周角定理即可得到结论.
【解答】解:∵四边形ABCD内接于⊙O,∠D=100°,
∴∠ABC=180°﹣∠D=80°,
∵CE⊥AB,
∴∠ECB+∠ABC=90°,
∴∠BCE=90°﹣80°=10°,
∵在同圆或等圆中,圆周角是所对弧的圆心角的一半,
∴∠BOE=2∠BCE=20°,
故选:B.
【点评】本题考查了圆内接四边形的性质,三角形的内角和定理,垂直的定义,圆周角定理,正确的识别图形是解题的关键.
8.如图,四边形ABCD为⊙O的内接四边形,已知∠BCD为120°,则∠BOD的度数为( )
A.100°
B.110°
C.120°
D.130°
【分析】根据圆内接四边形的性质求出∠A,根据圆周角定理计算,得到答案.
【解答】解:∵四边形ABCD是⊙O的内接四边形,
∴∠A=180°﹣∠BCD=60°,
由圆周角定理得,∠BOD=2∠A=120°,
故选:C.
【点评】本题考查的是圆内接四边形的性质,掌握圆内接四边形的对角互补是解题的关键.
9.如图,四边形ABCD是⊙O的内接四边形,∠A=125°,则∠BOD的度数为( )
A.55°
B.65°
C.110°
D.125°
【分析】根据圆内接四边形的性质求出∠C的度数,根据圆周角定理计算即可.
【解答】解:∵四边形ABCD为⊙O的内接四边形,∠A=125°,
∴∠C=180°﹣∠A=55°,
∴∠BOD=2∠A=110°,
故选:C.
【点评】本题考查的是圆内接四边形的性质和圆周角定理,掌握圆内接四边形的对角互补是解题的关键.
二.填空题(共6小题)
10.如图,扇形OAB中,∠AOB=60°,OA=4,点C为弧AB的中点,D为半径OA上一点,点A关于直线CD的对称点为E,若点E落在半径OA上,则OE= 4﹣4 .
【分析】连接OC,作EF⊥OC于F,根据圆心角、弧、弦的关系定理得到∠AOC=30°,根据等腰三角形的性质、三角形内角和定理得到∠ECF=45°,根据正切的定义列式计算,得到答案.
【解答】解:连接OC,作EF⊥OC于F,
∵点A关于直线CD的对称点为E,点E落在半径OA上,
∴CE=CA,
∵=,
∴∠AOC=∠AOB=30°,
∵OA=OC,
∴∠OAC=∠OCA=75°,
∵CE=CA,
∴∠CAE=∠CEA=75°,
∴∠CAE=30°,
∴∠ECF=45°,
设EF=x,则FC=x,
在Rt△EOF中,tan∠EOF=,
∴OF==x,
由题意得,OF+FC=OC,即x+x=4,
解得,x=2﹣2,
∵∠EOF=30°,
∴OE=2EF=4﹣4,
故答案为:4﹣4.
【点评】本题考查的是圆心角、弧、弦的关系、解直角三角形的应用、三角形内角和定理,掌握锐角三角函数的定义是解题的关键.
11.长度等于6的弦所对的圆心角是90°,则该圆半径为 6 .
【分析】由45度角直角三角形边角关系解答即可.
【解答】解:如图AB=6,∠AOB=90°,
∵OA=OB,
∴OA=OB===6,
故答案为6.
【点评】本题考查了特殊直角三角形边角关系,熟练掌握45度角直角三角形边角关系是解题的关键.
12.如图,⊙O为锐角ABC的外接圆,若∠BAO=15°,则∠C的度数为 75° .
【分析】连接OB,如图,利用等腰三角形的性质和三角形内角和计算出∠AOB=150°,然后根据圆周角定理计算∠C的度数.
【解答】解:连接OB,如图,
∵OA=OB,
∴∠OBA=∠OAB=15°,
∴∠AOB=180°﹣15°﹣15°=150°,
∴∠C=∠AOB=75°.
故答案为75°.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
13.如图,AB为⊙O的直径,C,D为⊙O上的点,=.若∠CAB=50°,则∠CAD= 20 °.
【分析】连接OC,OD,由圆周角定理得出∠COB=100°,结合=可求出∠COD的度数,再利用圆周角定理即可求出∠CAD的度数.
【解答】解:连接OC,OD,如图所示:
∵∠CAB=50°,
∴∠COB=2∠AB=100°.
∵=,
∴∠AOD=∠COD=(180°﹣∠COB)=40°,
∴∠CAD=∠COD=20°.
故答案为:20.
【点评】本题考查了圆周角定理以及圆心角、弧、弦的关系,熟练掌握圆周角定理,利用等弧对的圆心角相等,求出∠COD的度数是解题的关键.
14.如图,点O为线段BC的中点,点A、C、D到点O的距离相等,若∠ABC=50°,则∠ADC的度数是 130 °.
【分析】根据题意得到四点A、B、C、D共圆,利用圆内接四边形对角互补即可求出所求角的度数.
【解答】解:由题意得到OA=OB=OC=OD,作出圆O,如图所示,
∴四边形ABCD为圆O的内接四边形,
∴∠ABC+∠ADC=180°,
∵∠ABC=50°,
∴∠ADC=130°,
故答案为:130.
【点评】此题考查了圆内接四边形的性质,熟练掌握圆内接四边形的性质是解本题的关键.
15.如图,四边形ABCD内接于⊙O,且四边形OABC是平行四边形,则∠D= 60° .
【分析】直接利用平行四边形的性质得出∠AOC=∠ABC,再利用圆周角定理、圆内接四边形的性质得出,∠D=∠AOC=∠ABC,进而得出答案.
【解答】解:∵四边形OABC是平行四边形,
∴∠AOC=∠ABC,
∵∠D+∠ABC=180°,∠D=∠AOC=∠ABC,
∴设∠D=x,则∠ABC=2x,
∴x+2x=180°,
解得:x=60°,
故∠D=60°.
故答案为:60°.
【点评】此题主要考查了圆内接四边形的性质以及平行四边形的性质,正确得出∠D=∠AOC=∠ABC是解题关键.
三.解答题(共3小题)
16.如图,在⊙O中,=,CD⊥OA于点D,CE⊥OB于点E.
(1)求证:CD=CE;
(2)若∠AOB=120°,OA=2,求四边形DOEC的面积.
【分析】(1)连接OC,根据圆心角、弧、弦的关系定理得到∠AOC=∠BOC,根据角平分线的性质定理证明结论;
(2)根据直角三角形的性质求出OD,根据勾股定理求出CD,根据三角形的面积公式计算,得到答案.
【解答】(1)证明:连接OC,
∵=,
∴∠AOC=∠BOC,又CD⊥OA,CE⊥OB,
∴CD=CE;
(2)解:∵∠AOB=120°,
∴∠AOC=∠BOC=60°,
∵∠CDO=90°,
∴∠OCD=30°,
∴OD=OC=1,
∴CD===,
∴△OCD的面积=×OD×CD=,
同理可得,△OCE的面积=×OD×CD=,
∴四边形DOEC的面积=+=.
【点评】本题考查的是圆心角、弧、弦的关系定理、勾股定理、直角三角形的性质,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
17.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,延长CA交⊙O于点E.连结ED交AB于点F.
(1)求证:△CDE是等腰三角形.
(2)当CD:AC=2:时,求的值.
【分析】(1)由等腰三角形的性质得出∠ABC=∠C,由圆周角定理得出∠AED=∠B,证出∠AED=∠C,即可得出结论;
(2)连接AD,过点D作DH⊥AE于点H,设CD=2x,AC=x,则AD=x,由三角形ADC的面积可得出DH的长,求出AE,则可得出答案.
【解答】解:(1)证明:∵AB=AC,
∴∠ABC=∠C,
∵=,
∴∠AED=∠ABC,
∴∠C=∠AED,
∴△CDE是等腰三角形;
(2)如图,连接AD,过点D作DH⊥AE于点H,
设CD=2x,AC=x,
∵AB是直径,
∴∠ADC=90°,
∴AD==x,
∵S△ADC=AD?DC=AC?DH,
∴DH=x,
∵DE=CD,
∴CH=EH==x,
∴AE=2CH﹣AC=x.
∴=.
【点评】本题考查了等腰三角形的判定与性质,圆周角定理,勾股定理,三角形的面积等知识,熟练掌握圆周角定理是解题的关键.
18.(1)解方程:x2﹣2x﹣24=0.
(2)如图,A,B,C,D四点都在⊙O上,BD为直径,四边形OABC是平行四边形,求∠D的度数.
【分析】(1)首先把左边分解因式,然后可得一元一次方程,再解即可;
(2)首先判定四边形OABC是菱形,再证明△OBC是等边三角形,进而可得∠COB=60°,然后可得答案.
【解答】解:(1)x2﹣2x﹣24=0,
(x﹣6)(x+4)=0,
则x﹣6=0或x+4=0,
解得:x1=6,x2=﹣4;
(2)∵四边形OABC是平行四边形,OA=OC,
∴四边形OABC是菱形,
∴AO=CB,
∵CO=BO=AO,
∴△OBC是等边三角形,
∴∠COB=60°,
∵BD为直径,
∴∠DCB=90°,
∴∠D=30°.
【点评】此题主要考查了一元二次方程的解法,以及平行四边形的性质和菱形的判定,关键是掌握因式分解法解一元二次方程的步骤,掌握邻边相等的平行四边形是菱形.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/8
10:33:43;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
24.1
圆的有关性质(2)
一.选择题(共9小题)
1.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是( )
A.
B.3
C.3
D.4
2.如图,将大小不同的两块量角器的零度线对齐,且小量角器的中心O2,恰好在大量角器的圆周上,设图中两圆周的交点为P,且点P在小量角器上对应的刻度为63°,那么点P在大量角器上对应的刻度为(只考虑小于90°的角)( )
A.54°
B.55°
C.56°
D.57°
3.如图,圆O通过五边形OABCD的四个顶点.若=150°,∠A=75°,∠D=60°,则的度数为何?( )
A.25°
B.40°
C.50°
D.60°
4.如图,在⊙O中,直径AB⊥CD,∠A=26°,则∠D度数是( )
A.26°
B.38°
C.52°
D.64°
5.如图,AB为⊙O的直径,C,D是圆周上的两点,若∠ABC=38°,则锐角∠BDC的度数为( )
A.57°
B.52°
C.38°
D.26°
6.如图,A、B、C三点在⊙O上,D是CB延长线上的一点,∠ABD=40°,那么∠AOC的度数为( )
A.80°
B.70°
C.50°
D.40°
7.如图,四边形ABCD内接于⊙O,∠D=100°,CE⊥AB交⊙O于点E,连接OB、OE,则∠BOE的度数为( )
A.18°
B.20°
C.25°
D.40°
8.如图,四边形ABCD为⊙O的内接四边形,已知∠BCD为120°,则∠BOD的度数为( )
A.100°
B.110°
C.120°
D.130°
9.如图,四边形ABCD是⊙O的内接四边形,∠A=125°,则∠BOD的度数为( )
A.55°
B.65°
C.110°
D.125°
二.填空题(共6小题)
10.如图,扇形OAB中,∠AOB=60°,OA=4,点C为弧AB的中点,D为半径OA上一点,点A关于直线CD的对称点为E,若点E落在半径OA上,则OE=
.
11.长度等于6的弦所对的圆心角是90°,则该圆半径为
.
12.如图,⊙O为锐角ABC的外接圆,若∠BAO=15°,则∠C的度数为
.
13.如图,AB为⊙O的直径,C,D为⊙O上的点,=.若∠CAB=50°,则∠CAD=
°.
14.如图,点O为线段BC的中点,点A、C、D到点O的距离相等,若∠ABC=50°,则∠ADC的度数是
°.
15.如图,四边形ABCD内接于⊙O,且四边形OABC是平行四边形,则∠D=
.
三.解答题(共3小题)
16.如图,在⊙O中,=,CD⊥OA于点D,CE⊥OB于点E.
(1)求证:CD=CE;
(2)若∠AOB=120°,OA=2,求四边形DOEC的面积.
17.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,延长CA交⊙O于点E.连结ED交AB于点F.
(1)求证:△CDE是等腰三角形.
(2)当CD:AC=2:时,求的值.
18.(1)解方程:x2﹣2x﹣24=0.
(2)如图,A,B,C,D四点都在⊙O上,BD为直径,四边形OABC是平行四边形,求∠D的度数.
24.1
圆的有关性质(2)
参考答案与试题解析
一.选择题(共9小题)
1.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是( )
A.
B.3
C.3
D.4
【分析】连接OD,交AC于F,根据垂径定理得出OD⊥AC,AF=CF,进而证得DF=BC,根据三角形中位线定理求得OF=BC=DF,从而求得BC=DF=2,利用勾股定理即可求得AC.
【解答】解:连接OD,交AC于F,
∵D是的中点,
∴OD⊥AC,AF=CF,
∴∠DFE=90°,
∵OA=OB,AF=CF,
∴OF=BC,
∵AB是直径,
∴∠ACB=90°,
在△EFD和△ECB中
∴△EFD≌△ECB(AAS),
∴DF=BC,
∴OF=DF,
∵OD=3,
∴OF=1,
∴BC=2,
在Rt△ABC中,AC2=AB2﹣BC2,
∴AC===4,
故选:D.
【点评】本题考查了垂径定理,三角形全等的判定和性质,三角形中位线定理,熟练掌握性质定理是解题的关键.
2.如图,将大小不同的两块量角器的零度线对齐,且小量角器的中心O2,恰好在大量角器的圆周上,设图中两圆周的交点为P,且点P在小量角器上对应的刻度为63°,那么点P在大量角器上对应的刻度为(只考虑小于90°的角)( )
A.54°
B.55°
C.56°
D.57°
【分析】连接O1P,O2P,如图,先根据O1P=O2P得到∠O1PO2=∠O1O2P=63°,然后根据三角形内角和求出∠PO1O2即可.
【解答】解:连接O1P,O2P,如图,
∵P在小量角器上对应的刻度为63°,
即∠O1O2P=63°,
而O1P=O2P,
∴∠O1PO2=∠O1O2P=63°,
∴∠PO1O2=180°﹣63°﹣63°=54°,
即点P在大量角器上对应的刻度为54°(只考虑小于90°的角).
故选:A.
【点评】本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
3.如图,圆O通过五边形OABCD的四个顶点.若=150°,∠A=75°,∠D=60°,则的度数为何?( )
A.25°
B.40°
C.50°
D.60°
【分析】连接OB,OC,由半径相等得到△OAB,△OBC,△OCD都为等腰三角形,根据∠A=75°,∠D=60°,求出∠1与∠2的度数,根据的度数确定出∠AOD度数,进而求出∠3的度数,即可确定出的度数.
【解答】解:连接OB、OC,
∵OA=OB=OC=OD,
∴△OAB、△OBC、△OCD,皆为等腰三角形,
∵∠A=65°,∠D=60°,
∴∠1=180°﹣2∠A=180°﹣2×75°=30°,∠2=180°﹣2∠D=180°﹣2×60°=60°,
∵=150°,
∴∠AOD=150°,
∴∠3=∠AOD﹣∠1﹣∠2=150°﹣30°﹣60°=60°,
则的度数为60°.
故选:D.
【点评】此题考查了圆心角、弧、弦的关系,多边形内角与外角,弄清圆心角、弧、弦的关系是解本题的关键.
4.如图,在⊙O中,直径AB⊥CD,∠A=26°,则∠D度数是( )
A.26°
B.38°
C.52°
D.64°
【分析】连接OC,如图,先根据圆周角定理得到∠BOC=2∠A=52°,再利用互余计算出∠OCD=38°,然后利用等腰三角形的性质得到∠D的度数.
【解答】解:连接OC,如图,
∵∠A=26°,
∴∠BOC=2∠A=52°,
∵AB⊥CD,
∴∠OCD=90°﹣∠BOC=90°﹣52°=38°,
∵OC=OD,
∴∠D=∠OCD=38°.
故选:B.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
5.如图,AB为⊙O的直径,C,D是圆周上的两点,若∠ABC=38°,则锐角∠BDC的度数为( )
A.57°
B.52°
C.38°
D.26°
【分析】由AB是⊙O的直径,根据直径所对的圆周角是直角,即可得∠ACB=90°,又由∠ABC=38°,即可求得∠A的度数,然后根据在同圆或等圆中,同弧或等弧所对的圆周角相等,即可求得∠BDC的度数.
【解答】解:连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠ABC=38°,
∴∠BAC=90°﹣∠ABC=52°,
∴∠BDC=∠BAC=52°.
故选:B.
【点评】此题考查了圆周角定理.此题难度不大,注意掌握直径所对的圆周角是直角与在同圆或等圆中,同弧或等弧所对的圆周角相等定理的应用是解此题的关键.
6.如图,A、B、C三点在⊙O上,D是CB延长线上的一点,∠ABD=40°,那么∠AOC的度数为( )
A.80°
B.70°
C.50°
D.40°
【分析】作所对的圆周角∠AEC,如图,先利用邻补角计算出∠ABC=140°,再利用圆内接四边形的性质计算出∠E=40°,然后根据圆周角定理得到∠AOC的度数.
【解答】解:所对的圆周角∠AEC,如图,
∵∠ABD=40°,
∴∠ABC=180°﹣40°=140°,
∵∠AEC+∠ABC=180°,
∴∠E=40°,
∴∠AOC=2∠AEC=2×40°=80°.
故选:A.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
7.如图,四边形ABCD内接于⊙O,∠D=100°,CE⊥AB交⊙O于点E,连接OB、OE,则∠BOE的度数为( )
A.18°
B.20°
C.25°
D.40°
【分析】根据圆内接四边形的性质和圆周角定理即可得到结论.
【解答】解:∵四边形ABCD内接于⊙O,∠D=100°,
∴∠ABC=180°﹣∠D=80°,
∵CE⊥AB,
∴∠ECB+∠ABC=90°,
∴∠BCE=90°﹣80°=10°,
∵在同圆或等圆中,圆周角是所对弧的圆心角的一半,
∴∠BOE=2∠BCE=20°,
故选:B.
【点评】本题考查了圆内接四边形的性质,三角形的内角和定理,垂直的定义,圆周角定理,正确的识别图形是解题的关键.
8.如图,四边形ABCD为⊙O的内接四边形,已知∠BCD为120°,则∠BOD的度数为( )
A.100°
B.110°
C.120°
D.130°
【分析】根据圆内接四边形的性质求出∠A,根据圆周角定理计算,得到答案.
【解答】解:∵四边形ABCD是⊙O的内接四边形,
∴∠A=180°﹣∠BCD=60°,
由圆周角定理得,∠BOD=2∠A=120°,
故选:C.
【点评】本题考查的是圆内接四边形的性质,掌握圆内接四边形的对角互补是解题的关键.
9.如图,四边形ABCD是⊙O的内接四边形,∠A=125°,则∠BOD的度数为( )
A.55°
B.65°
C.110°
D.125°
【分析】根据圆内接四边形的性质求出∠C的度数,根据圆周角定理计算即可.
【解答】解:∵四边形ABCD为⊙O的内接四边形,∠A=125°,
∴∠C=180°﹣∠A=55°,
∴∠BOD=2∠A=110°,
故选:C.
【点评】本题考查的是圆内接四边形的性质和圆周角定理,掌握圆内接四边形的对角互补是解题的关键.
二.填空题(共6小题)
10.如图,扇形OAB中,∠AOB=60°,OA=4,点C为弧AB的中点,D为半径OA上一点,点A关于直线CD的对称点为E,若点E落在半径OA上,则OE= 4﹣4 .
【分析】连接OC,作EF⊥OC于F,根据圆心角、弧、弦的关系定理得到∠AOC=30°,根据等腰三角形的性质、三角形内角和定理得到∠ECF=45°,根据正切的定义列式计算,得到答案.
【解答】解:连接OC,作EF⊥OC于F,
∵点A关于直线CD的对称点为E,点E落在半径OA上,
∴CE=CA,
∵=,
∴∠AOC=∠AOB=30°,
∵OA=OC,
∴∠OAC=∠OCA=75°,
∵CE=CA,
∴∠CAE=∠CEA=75°,
∴∠CAE=30°,
∴∠ECF=45°,
设EF=x,则FC=x,
在Rt△EOF中,tan∠EOF=,
∴OF==x,
由题意得,OF+FC=OC,即x+x=4,
解得,x=2﹣2,
∵∠EOF=30°,
∴OE=2EF=4﹣4,
故答案为:4﹣4.
【点评】本题考查的是圆心角、弧、弦的关系、解直角三角形的应用、三角形内角和定理,掌握锐角三角函数的定义是解题的关键.
11.长度等于6的弦所对的圆心角是90°,则该圆半径为 6 .
【分析】由45度角直角三角形边角关系解答即可.
【解答】解:如图AB=6,∠AOB=90°,
∵OA=OB,
∴OA=OB===6,
故答案为6.
【点评】本题考查了特殊直角三角形边角关系,熟练掌握45度角直角三角形边角关系是解题的关键.
12.如图,⊙O为锐角ABC的外接圆,若∠BAO=15°,则∠C的度数为 75° .
【分析】连接OB,如图,利用等腰三角形的性质和三角形内角和计算出∠AOB=150°,然后根据圆周角定理计算∠C的度数.
【解答】解:连接OB,如图,
∵OA=OB,
∴∠OBA=∠OAB=15°,
∴∠AOB=180°﹣15°﹣15°=150°,
∴∠C=∠AOB=75°.
故答案为75°.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
13.如图,AB为⊙O的直径,C,D为⊙O上的点,=.若∠CAB=50°,则∠CAD= 20 °.
【分析】连接OC,OD,由圆周角定理得出∠COB=100°,结合=可求出∠COD的度数,再利用圆周角定理即可求出∠CAD的度数.
【解答】解:连接OC,OD,如图所示:
∵∠CAB=50°,
∴∠COB=2∠AB=100°.
∵=,
∴∠AOD=∠COD=(180°﹣∠COB)=40°,
∴∠CAD=∠COD=20°.
故答案为:20.
【点评】本题考查了圆周角定理以及圆心角、弧、弦的关系,熟练掌握圆周角定理,利用等弧对的圆心角相等,求出∠COD的度数是解题的关键.
14.如图,点O为线段BC的中点,点A、C、D到点O的距离相等,若∠ABC=50°,则∠ADC的度数是 130 °.
【分析】根据题意得到四点A、B、C、D共圆,利用圆内接四边形对角互补即可求出所求角的度数.
【解答】解:由题意得到OA=OB=OC=OD,作出圆O,如图所示,
∴四边形ABCD为圆O的内接四边形,
∴∠ABC+∠ADC=180°,
∵∠ABC=50°,
∴∠ADC=130°,
故答案为:130.
【点评】此题考查了圆内接四边形的性质,熟练掌握圆内接四边形的性质是解本题的关键.
15.如图,四边形ABCD内接于⊙O,且四边形OABC是平行四边形,则∠D= 60° .
【分析】直接利用平行四边形的性质得出∠AOC=∠ABC,再利用圆周角定理、圆内接四边形的性质得出,∠D=∠AOC=∠ABC,进而得出答案.
【解答】解:∵四边形OABC是平行四边形,
∴∠AOC=∠ABC,
∵∠D+∠ABC=180°,∠D=∠AOC=∠ABC,
∴设∠D=x,则∠ABC=2x,
∴x+2x=180°,
解得:x=60°,
故∠D=60°.
故答案为:60°.
【点评】此题主要考查了圆内接四边形的性质以及平行四边形的性质,正确得出∠D=∠AOC=∠ABC是解题关键.
三.解答题(共3小题)
16.如图,在⊙O中,=,CD⊥OA于点D,CE⊥OB于点E.
(1)求证:CD=CE;
(2)若∠AOB=120°,OA=2,求四边形DOEC的面积.
【分析】(1)连接OC,根据圆心角、弧、弦的关系定理得到∠AOC=∠BOC,根据角平分线的性质定理证明结论;
(2)根据直角三角形的性质求出OD,根据勾股定理求出CD,根据三角形的面积公式计算,得到答案.
【解答】(1)证明:连接OC,
∵=,
∴∠AOC=∠BOC,又CD⊥OA,CE⊥OB,
∴CD=CE;
(2)解:∵∠AOB=120°,
∴∠AOC=∠BOC=60°,
∵∠CDO=90°,
∴∠OCD=30°,
∴OD=OC=1,
∴CD===,
∴△OCD的面积=×OD×CD=,
同理可得,△OCE的面积=×OD×CD=,
∴四边形DOEC的面积=+=.
【点评】本题考查的是圆心角、弧、弦的关系定理、勾股定理、直角三角形的性质,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
17.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,延长CA交⊙O于点E.连结ED交AB于点F.
(1)求证:△CDE是等腰三角形.
(2)当CD:AC=2:时,求的值.
【分析】(1)由等腰三角形的性质得出∠ABC=∠C,由圆周角定理得出∠AED=∠B,证出∠AED=∠C,即可得出结论;
(2)连接AD,过点D作DH⊥AE于点H,设CD=2x,AC=x,则AD=x,由三角形ADC的面积可得出DH的长,求出AE,则可得出答案.
【解答】解:(1)证明:∵AB=AC,
∴∠ABC=∠C,
∵=,
∴∠AED=∠ABC,
∴∠C=∠AED,
∴△CDE是等腰三角形;
(2)如图,连接AD,过点D作DH⊥AE于点H,
设CD=2x,AC=x,
∵AB是直径,
∴∠ADC=90°,
∴AD==x,
∵S△ADC=AD?DC=AC?DH,
∴DH=x,
∵DE=CD,
∴CH=EH==x,
∴AE=2CH﹣AC=x.
∴=.
【点评】本题考查了等腰三角形的判定与性质,圆周角定理,勾股定理,三角形的面积等知识,熟练掌握圆周角定理是解题的关键.
18.(1)解方程:x2﹣2x﹣24=0.
(2)如图,A,B,C,D四点都在⊙O上,BD为直径,四边形OABC是平行四边形,求∠D的度数.
【分析】(1)首先把左边分解因式,然后可得一元一次方程,再解即可;
(2)首先判定四边形OABC是菱形,再证明△OBC是等边三角形,进而可得∠COB=60°,然后可得答案.
【解答】解:(1)x2﹣2x﹣24=0,
(x﹣6)(x+4)=0,
则x﹣6=0或x+4=0,
解得:x1=6,x2=﹣4;
(2)∵四边形OABC是平行四边形,OA=OC,
∴四边形OABC是菱形,
∴AO=CB,
∵CO=BO=AO,
∴△OBC是等边三角形,
∴∠COB=60°,
∵BD为直径,
∴∠DCB=90°,
∴∠D=30°.
【点评】此题主要考查了一元二次方程的解法,以及平行四边形的性质和菱形的判定,关键是掌握因式分解法解一元二次方程的步骤,掌握邻边相等的平行四边形是菱形.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/8
10:33:43;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
同课章节目录
