4.1 几何图形 同步练习(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
4.1
几何图形
一.认识立体图形(共6小题)
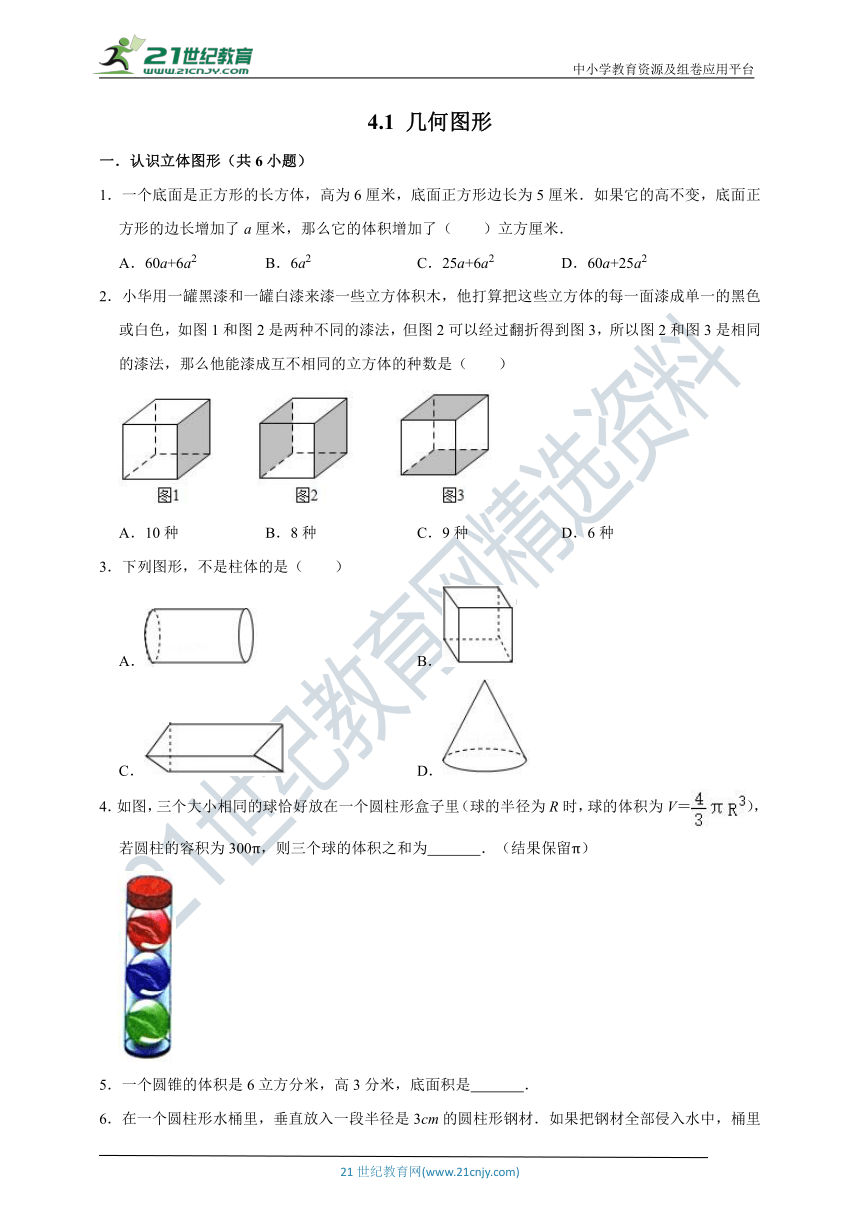
1.一个底面是正方形的长方体,高为6厘米,底面正方形边长为5厘米.如果它的高不变,底面正方形的边长增加了a厘米,那么它的体积增加了( )立方厘米.
A.60a+6a2
B.6a2
C.25a+6a2
D.60a+25a2
2.小华用一罐黑漆和一罐白漆来漆一些立方体积木,他打算把这些立方体的每一面漆成单一的黑色或白色,如图1和图2是两种不同的漆法,但图2可以经过翻折得到图3,所以图2和图3是相同的漆法,那么他能漆成互不相同的立方体的种数是( )
A.10种
B.8种
C.9种
D.6种
3.下列图形,不是柱体的是( )
A.
B.
C.
D.
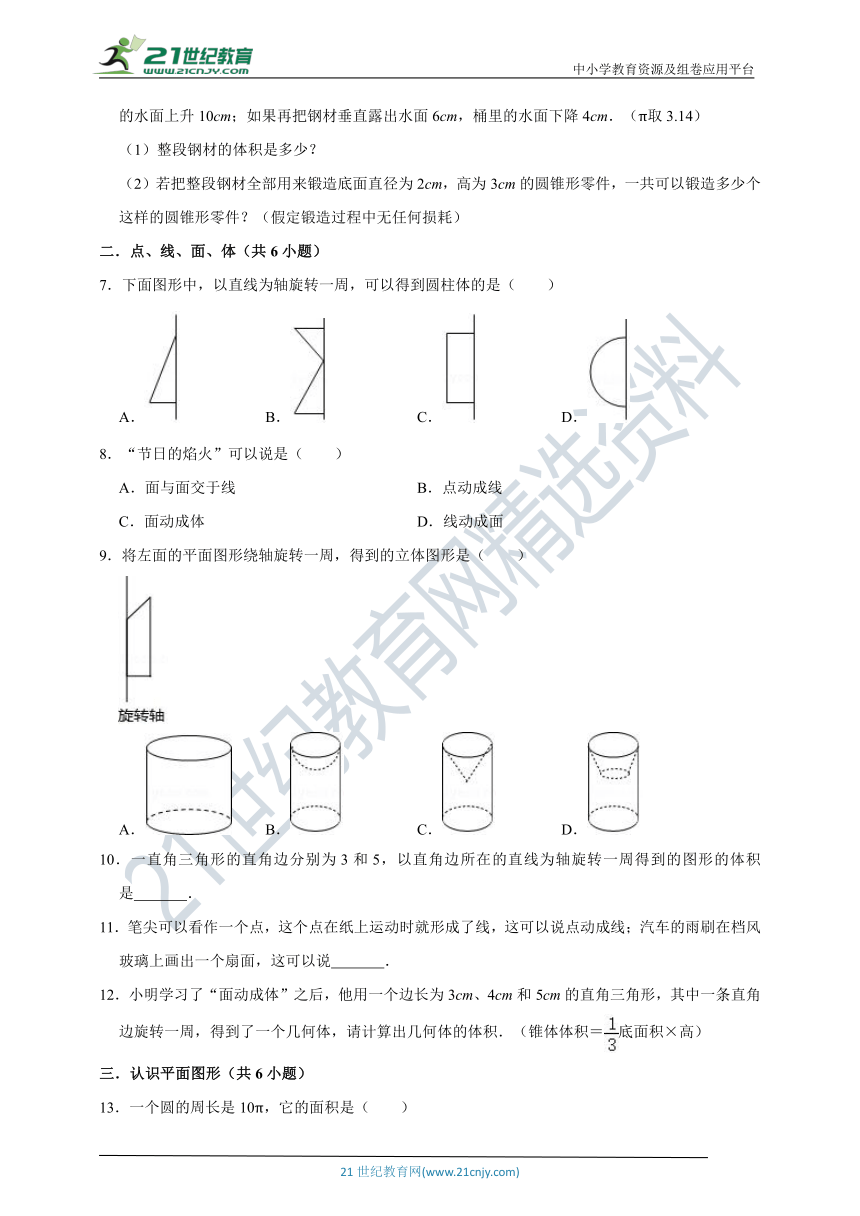
4.如图,三个大小相同的球恰好放在一个圆柱形盒子里(球的半径为R时,球的体积为V=),若圆柱的容积为300π,则三个球的体积之和为
.(结果保留π)
5.一个圆锥的体积是6立方分米,高3分米,底面积是
.
6.在一个圆柱形水桶里,垂直放入一段半径是3cm的圆柱形钢材.如果把钢材全部侵入水中,桶里的水面上升10cm;如果再把钢材垂直露出水面6cm,桶里的水面下降4cm.(π取3.14)
(1)整段钢材的体积是多少?
(2)若把整段钢材全部用来锻造底面直径为2cm,高为3cm的圆锥形零件,一共可以锻造多少个这样的圆锥形零件?(假定锻造过程中无任何损耗)
二.点、线、面、体(共6小题)
7.下面图形中,以直线为轴旋转一周,可以得到圆柱体的是( )
A.
B.
C.
D.
8.“节日的焰火”可以说是( )
A.面与面交于线
B.点动成线
C.面动成体
D.线动成面
9.将左面的平面图形绕轴旋转一周,得到的立体图形是( )
A.
B.
C.
D.
10.一直角三角形的直角边分别为3和5,以直角边所在的直线为轴旋转一周得到的图形的体积是
.
11.笔尖可以看作一个点,这个点在纸上运动时就形成了线,这可以说点动成线;汽车的雨刷在档风玻璃上画出一个扇面,这可以说
.
12.小明学习了“面动成体”之后,他用一个边长为3cm、4cm和5cm的直角三角形,其中一条直角边旋转一周,得到了一个几何体,请计算出几何体的体积.(锥体体积=底面积×高)
三.认识平面图形(共6小题)
13.一个圆的周长是10π,它的面积是( )
A.25π
B.5π
C.100π
D.10π
14.在一个长8厘米,宽7厘米的长方形里面画一个最大的圆,圆规两脚之间的距离是( )厘米.
A.7
B.4
C.3.5
D.3
15.如图,一个大长方形恰好被分割成四个正方形,则涂色的小正方形面积是整个长方形面积的( )
A.
B.
C.
D.
16.如图:已知小正方形的面积是16平方厘米,则圆的面积是
平方厘米.
17.如果圆的周长是62.8厘米,那么这个圆的面积是
平方厘米.
18.有一个著名的希波克拉蒂月牙问题.如图:以AB为直径作半圆,C是圆弧上一点,(不与A、B重合),以AC、BC为直径分别作半圆,围成两个月牙形1、2(阴影部分).已知直径AC为4,直径BC为3,直径AB为5.
(1)分别求出三个半圆的面积(结果保留π);
(2)请你猜测,这两个月牙形的面积与三角形ABC的面积之间有何等量关系,请写出你的猜想,并通过计算说明.
4.1
几何图形
参考答案与试题解析
一.认识立体图形(共6小题)
1.一个底面是正方形的长方体,高为6厘米,底面正方形边长为5厘米.如果它的高不变,底面正方形的边长增加了a厘米,那么它的体积增加了( )立方厘米.
A.60a+6a2
B.6a2
C.25a+6a2
D.60a+25a2
【分析】长方体变化后的高为6厘米,底面边长为(5+a)厘米,根据长方体的体积公式求解.
【解答】解:6(a+5)2﹣6×52
=150+60a+6a2﹣150
=6a2+60a(立方厘米).
答:它的体积增加了(6a2+60a)立方厘米.
故选:A.
【点评】本题考查了完全平方公式,分别用整式表示两个长方体的体积,再求差,即可得到体积增加的值.
2.小华用一罐黑漆和一罐白漆来漆一些立方体积木,他打算把这些立方体的每一面漆成单一的黑色或白色,如图1和图2是两种不同的漆法,但图2可以经过翻折得到图3,所以图2和图3是相同的漆法,那么他能漆成互不相同的立方体的种数是( )
A.10种
B.8种
C.9种
D.6种
【分析】利用表格法枚举出所有可能性即可.
【解答】解:由题意可得:
他能漆成互不相同的立方体的种数是10.
故选:A.
【点评】本题主要考查了认识立体图形以及概率,解答本题的关键在于能列出所有满足的情况.
3.下列图形,不是柱体的是( )
A.
B.
C.
D.
【分析】根据柱体是上下一样粗的几何体可得答案.
【解答】解:长方体是四棱柱,三棱柱是柱体,圆锥是锥体,圆柱是柱体,
故选:D.
【点评】此题主要考查了认识立体图形,关键是掌握各种图形的特点.
4.如图,三个大小相同的球恰好放在一个圆柱形盒子里(球的半径为R时,球的体积为V=),若圆柱的容积为300π,则三个球的体积之和为 200π .(结果保留π)
【分析】根据圆柱体的体积和球的体积的计算公式即可得到结果.
【解答】解:设球的半径为r,
根据题意得:三个球的体积之和=3×πr3=4πr3,
圆柱体盒子容积=πr2?6r=6πr3,
=,
300π×=200π.
答:三个球的体积之和是200π.
故答案为:200π.
【点评】本题考查了圆柱体的体积,球的体积的计算,整式的混合运算,熟记圆柱体的体积和球的体积的计算公式是解题的关键.
5.一个圆锥的体积是6立方分米,高3分米,底面积是 6平方分米 .
【分析】根据圆锥的体积计算即可.
【解答】解:6×3÷3=6(平方分米).
故答案为:6平方分米.
【点评】本题考查了圆锥的体积公式,熟练掌握圆锥的体积公式是解题的关键.
6.在一个圆柱形水桶里,垂直放入一段半径是3cm的圆柱形钢材.如果把钢材全部侵入水中,桶里的水面上升10cm;如果再把钢材垂直露出水面6cm,桶里的水面下降4cm.(π取3.14)
(1)整段钢材的体积是多少?
(2)若把整段钢材全部用来锻造底面直径为2cm,高为3cm的圆锥形零件,一共可以锻造多少个这样的圆锥形零件?(假定锻造过程中无任何损耗)
【分析】(1)根据题意先求出整段钢材的高,再根据圆柱的体积公式列式计算即可;
(2)根据圆锥的体积公式求出每个圆锥形零件的体积,再用整段钢材的体积除以每个圆锥形零件的体积即可求解.
【解答】解:(1)整段钢材的高为:10×(6÷4)=15(cm),
整段钢材的体积为:3.14×32×15=423.9(cm3),
答:整段钢材的体积是423.9立方厘米;
(2)每个圆锥形零件的体积为,
锻造锥形零件的个数为:423.9÷3.14=135(个).
答:一共可以锻造135个这样的圆锥形零件.
【点评】考查了圆柱与圆锥的体积,解题关键是要读懂题目的意思,根据题目给出的条件,由体积公式找出合适的等量关系列出方程,再求解.
二.点、线、面、体(共6小题)
7.下面图形中,以直线为轴旋转一周,可以得到圆柱体的是( )
A.
B.
C.
D.
【分析】根据面动成体进行解答即可.
【解答】解:A、以直线为轴旋转一周可以得到圆锥,故此选项不合题意;
B、以直线为轴旋转一周可以得到两个圆锥,故此选项不合题意;
C、以直线为轴旋转一周可以得到圆柱,故此选项符合题意;
D、以直线为轴旋转一周可以得到球,故此选项不合题意;
故选:C.
【点评】此题主要考查了点、线、面、体,关键是掌握点动成线,线动成面,面动成体,人是常见几何体.
8.“节日的焰火”可以说是( )
A.面与面交于线
B.点动成线
C.面动成体
D.线动成面
【分析】根据节日的焰火的火的运动路线可知点动即可成线.
【解答】解:根据节日的焰火的火的运动路线,
可以认为节日的焰火的火就是一个点,可知点动即可成线.
故选:B.
【点评】此题主要考查了点、线、面、体的形成,根据题意认为节日的焰火的火就是一个点从而解决问题.
9.将左面的平面图形绕轴旋转一周,得到的立体图形是( )
A.
B.
C.
D.
【分析】根据面动成体,梯形绕上底边旋转是圆柱减圆锥,可得答案.
【解答】解:梯形绕上底边旋转是圆柱减圆锥,故C正确;
故选:C.
【点评】本题考查了点、线、面、体,利用面动成体,直角三角形绕直角边旋转是圆锥,矩形绕边旋转是圆柱.
10.一直角三角形的直角边分别为3和5,以直角边所在的直线为轴旋转一周得到的图形的体积是 15π或25π .
【分析】根据直角三角形绕直角边旋转得圆锥,根据圆锥的体积公式,可得答案.
【解答】解:高为3,半径为5,圆锥的体积是π×52×3=25π;
高为5,半径为3,圆锥的体积是π×32×5=15π;
故答案为:15π或25π.
【点评】本题考查了点线面体,利用直角三角形绕直角边旋转得圆锥是解题的关键,要分类讨论,以防遗漏.
11.笔尖可以看作一个点,这个点在纸上运动时就形成了线,这可以说点动成线;汽车的雨刷在档风玻璃上画出一个扇面,这可以说 线动成面 .
【分析】汽车的雨刷实际上是一条线,通过运动把玻璃上的雨水刷干净,所以应是线动成面.
【解答】解:汽车的雨刷实际上是一条线,通过运动把玻璃上的雨水刷干净,所以应是线动成面.
故答案为:线动成面.
【点评】此题考查了点、线、面、体,正确理解点线面体的概念是解题的关键.
12.小明学习了“面动成体”之后,他用一个边长为3cm、4cm和5cm的直角三角形,其中一条直角边旋转一周,得到了一个几何体,请计算出几何体的体积.(锥体体积=底面积×高)
【分析】根据三角形旋转是圆锥,分旋转轴是3cm和4cm两种情况可得几何体体积.
【解答】解:以4cm为轴体积为×π×32×4=12π,
以3cm为轴的体积为×π×42×3=16π.
【点评】本题考查了点线面体,利用三角形旋转是圆锥是解题关键.
三.认识平面图形(共6小题)
13.一个圆的周长是10π,它的面积是( )
A.25π
B.5π
C.100π
D.10π
【分析】根据圆的周长公式,由已知的周长求出圆的半径,利用圆的面积公式即可求出所求圆的面积.
【解答】解:设圆的半径为r,
∵圆的周长为10π,
∴2πr=10π,即r=5,
则圆的面积S=πr2=25π.
故选:A.
【点评】此题考查了圆的周长公式,以及圆的面积公式,根据周长求出圆的半径是解本题的关键.同时要求学生熟练掌握圆中的有关计算公式.
14.在一个长8厘米,宽7厘米的长方形里面画一个最大的圆,圆规两脚之间的距离是( )厘米.
A.7
B.4
C.3.5
D.3
【分析】根据在长方形里面画一个最大的圆的直径=长方形的宽即可得到结论.
【解答】解:∵在一个长8厘米,宽7厘米的长方形里面画一个最大的圆,
∴这个最大的圆的直径=长方形的宽7厘米,
∴圆规两脚之间的距离是=3.5(厘米),
故选:C.
【点评】本题考查了认识平面图形,正确的理解题意是解题的关键.
15.如图,一个大长方形恰好被分割成四个正方形,则涂色的小正方形面积是整个长方形面积的( )
A.
B.
C.
D.
【分析】设出涂色正方形的边长,表示其面积;再根据各个正方形之间的关系,表示出整个矩形的长、宽,求出面积即可得出答案.
【解答】解:设阴影正方形的边长为x,
则正方形①的边长为x,正方形②的边长为2x,正方形③的边长为3x,
所以,这个长方形的长为3x,高为5x,其面积为3x?5x=15x2,
又涂色正方形的面积为x?x=x2,
因此涂色的小正方形面积是整个长方形面积的,
故选:C.
【点评】考查基本平面图形的特征,通过图形直观,得出边长之间的关系是解决问题的关键.
16.如图:已知小正方形的面积是16平方厘米,则圆的面积是 50.24 平方厘米.
【分析】根据已知条件“小正方形的面积是16平方厘米,”结合图形得到小正方形的边长即为这个圆的半径,这个正方形的面积也是圆的半径的平方,根据圆的面积公式即可得到结论.
【解答】解:因为小正方形的面积是16平方厘米,所以小正方形的边长是4厘米,即圆的半径是4厘米,所以S=πr2=16π(平方厘米)≈50.24(平方厘米).
【点评】本题考查了认识平面图形,正方形和圆的面积的计算,正确的识别图形是解题的关键.
17.如果圆的周长是62.8厘米,那么这个圆的面积是 314 平方厘米.
【分析】根据圆的周长C=2πr和圆的面积公式S=πr2解答即可.
【解答】解:π取近似值3.14,
圆是半径为62.8÷3.14÷2=10(厘米),
S=πr2=3.14×102=314(平方厘米),
所以这个圆的面积是314平方厘米.
故答案为:314.
【点评】本题考查了圆的周长和面积的计算.解答本题的关键是记住圆的周长C=2πr和圆的面积公式S=πr2.
18.有一个著名的希波克拉蒂月牙问题.如图:以AB为直径作半圆,C是圆弧上一点,(不与A、B重合),以AC、BC为直径分别作半圆,围成两个月牙形1、2(阴影部分).已知直径AC为4,直径BC为3,直径AB为5.
(1)分别求出三个半圆的面积(结果保留π);
(2)请你猜测,这两个月牙形的面积与三角形ABC的面积之间有何等量关系,请写出你的猜想,并通过计算说明.
【分析】(1)根据圆的面积公式进行计算即可,
(2)利用面积之间的关系可得两个月牙形的面积之和等于三角形ABC的面积.
【解答】解:(1)以AB为直径的半圆:
SAB为直径=π×()2=π,
以AC为直径的半圆:
SAC为直径=π×22=2π,
以BC为直径的半圆:
SBC为直径=π×()2=π,
∴SAB为直径=SAC为直径+SBC为直径=π,
(2)两个月牙形的面积之和等于三角形ABC的面积.
如图,四个月牙的面积依次为S1,S2,S3,S4,
于是,S1+S2=SBC为直径=π,S3+S4=SBC为直径=2π,
∴S1+S2+S3+S4=SBC为直径+SBC为直径=SAB为直径=S2+S4+S△ABC,
∴S1+S3=S△ABC,
即:两个月牙形的面积之和等于三角形ABC的面积.
【点评】考查圆的面积的计算方法,理清图形中各个部分面积之间的关系是解决问题的关键.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/11
9:50:10;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
4.1
几何图形
一.认识立体图形(共6小题)
1.一个底面是正方形的长方体,高为6厘米,底面正方形边长为5厘米.如果它的高不变,底面正方形的边长增加了a厘米,那么它的体积增加了( )立方厘米.
A.60a+6a2
B.6a2
C.25a+6a2
D.60a+25a2
2.小华用一罐黑漆和一罐白漆来漆一些立方体积木,他打算把这些立方体的每一面漆成单一的黑色或白色,如图1和图2是两种不同的漆法,但图2可以经过翻折得到图3,所以图2和图3是相同的漆法,那么他能漆成互不相同的立方体的种数是( )
A.10种
B.8种
C.9种
D.6种
3.下列图形,不是柱体的是( )
A.
B.
C.
D.
4.如图,三个大小相同的球恰好放在一个圆柱形盒子里(球的半径为R时,球的体积为V=),若圆柱的容积为300π,则三个球的体积之和为
.(结果保留π)
5.一个圆锥的体积是6立方分米,高3分米,底面积是
.
6.在一个圆柱形水桶里,垂直放入一段半径是3cm的圆柱形钢材.如果把钢材全部侵入水中,桶里的水面上升10cm;如果再把钢材垂直露出水面6cm,桶里的水面下降4cm.(π取3.14)
(1)整段钢材的体积是多少?
(2)若把整段钢材全部用来锻造底面直径为2cm,高为3cm的圆锥形零件,一共可以锻造多少个这样的圆锥形零件?(假定锻造过程中无任何损耗)
二.点、线、面、体(共6小题)
7.下面图形中,以直线为轴旋转一周,可以得到圆柱体的是( )
A.
B.
C.
D.
8.“节日的焰火”可以说是( )
A.面与面交于线
B.点动成线
C.面动成体
D.线动成面
9.将左面的平面图形绕轴旋转一周,得到的立体图形是( )
A.
B.
C.
D.
10.一直角三角形的直角边分别为3和5,以直角边所在的直线为轴旋转一周得到的图形的体积是
.
11.笔尖可以看作一个点,这个点在纸上运动时就形成了线,这可以说点动成线;汽车的雨刷在档风玻璃上画出一个扇面,这可以说
.
12.小明学习了“面动成体”之后,他用一个边长为3cm、4cm和5cm的直角三角形,其中一条直角边旋转一周,得到了一个几何体,请计算出几何体的体积.(锥体体积=底面积×高)
三.认识平面图形(共6小题)
13.一个圆的周长是10π,它的面积是( )
A.25π
B.5π
C.100π
D.10π
14.在一个长8厘米,宽7厘米的长方形里面画一个最大的圆,圆规两脚之间的距离是( )厘米.
A.7
B.4
C.3.5
D.3
15.如图,一个大长方形恰好被分割成四个正方形,则涂色的小正方形面积是整个长方形面积的( )
A.
B.
C.
D.
16.如图:已知小正方形的面积是16平方厘米,则圆的面积是
平方厘米.
17.如果圆的周长是62.8厘米,那么这个圆的面积是
平方厘米.
18.有一个著名的希波克拉蒂月牙问题.如图:以AB为直径作半圆,C是圆弧上一点,(不与A、B重合),以AC、BC为直径分别作半圆,围成两个月牙形1、2(阴影部分).已知直径AC为4,直径BC为3,直径AB为5.
(1)分别求出三个半圆的面积(结果保留π);
(2)请你猜测,这两个月牙形的面积与三角形ABC的面积之间有何等量关系,请写出你的猜想,并通过计算说明.
4.1
几何图形
参考答案与试题解析
一.认识立体图形(共6小题)
1.一个底面是正方形的长方体,高为6厘米,底面正方形边长为5厘米.如果它的高不变,底面正方形的边长增加了a厘米,那么它的体积增加了( )立方厘米.
A.60a+6a2
B.6a2
C.25a+6a2
D.60a+25a2
【分析】长方体变化后的高为6厘米,底面边长为(5+a)厘米,根据长方体的体积公式求解.
【解答】解:6(a+5)2﹣6×52
=150+60a+6a2﹣150
=6a2+60a(立方厘米).
答:它的体积增加了(6a2+60a)立方厘米.
故选:A.
【点评】本题考查了完全平方公式,分别用整式表示两个长方体的体积,再求差,即可得到体积增加的值.
2.小华用一罐黑漆和一罐白漆来漆一些立方体积木,他打算把这些立方体的每一面漆成单一的黑色或白色,如图1和图2是两种不同的漆法,但图2可以经过翻折得到图3,所以图2和图3是相同的漆法,那么他能漆成互不相同的立方体的种数是( )
A.10种
B.8种
C.9种
D.6种
【分析】利用表格法枚举出所有可能性即可.
【解答】解:由题意可得:
他能漆成互不相同的立方体的种数是10.
故选:A.
【点评】本题主要考查了认识立体图形以及概率,解答本题的关键在于能列出所有满足的情况.
3.下列图形,不是柱体的是( )
A.
B.
C.
D.
【分析】根据柱体是上下一样粗的几何体可得答案.
【解答】解:长方体是四棱柱,三棱柱是柱体,圆锥是锥体,圆柱是柱体,
故选:D.
【点评】此题主要考查了认识立体图形,关键是掌握各种图形的特点.
4.如图,三个大小相同的球恰好放在一个圆柱形盒子里(球的半径为R时,球的体积为V=),若圆柱的容积为300π,则三个球的体积之和为 200π .(结果保留π)
【分析】根据圆柱体的体积和球的体积的计算公式即可得到结果.
【解答】解:设球的半径为r,
根据题意得:三个球的体积之和=3×πr3=4πr3,
圆柱体盒子容积=πr2?6r=6πr3,
=,
300π×=200π.
答:三个球的体积之和是200π.
故答案为:200π.
【点评】本题考查了圆柱体的体积,球的体积的计算,整式的混合运算,熟记圆柱体的体积和球的体积的计算公式是解题的关键.
5.一个圆锥的体积是6立方分米,高3分米,底面积是 6平方分米 .
【分析】根据圆锥的体积计算即可.
【解答】解:6×3÷3=6(平方分米).
故答案为:6平方分米.
【点评】本题考查了圆锥的体积公式,熟练掌握圆锥的体积公式是解题的关键.
6.在一个圆柱形水桶里,垂直放入一段半径是3cm的圆柱形钢材.如果把钢材全部侵入水中,桶里的水面上升10cm;如果再把钢材垂直露出水面6cm,桶里的水面下降4cm.(π取3.14)
(1)整段钢材的体积是多少?
(2)若把整段钢材全部用来锻造底面直径为2cm,高为3cm的圆锥形零件,一共可以锻造多少个这样的圆锥形零件?(假定锻造过程中无任何损耗)
【分析】(1)根据题意先求出整段钢材的高,再根据圆柱的体积公式列式计算即可;
(2)根据圆锥的体积公式求出每个圆锥形零件的体积,再用整段钢材的体积除以每个圆锥形零件的体积即可求解.
【解答】解:(1)整段钢材的高为:10×(6÷4)=15(cm),
整段钢材的体积为:3.14×32×15=423.9(cm3),
答:整段钢材的体积是423.9立方厘米;
(2)每个圆锥形零件的体积为,
锻造锥形零件的个数为:423.9÷3.14=135(个).
答:一共可以锻造135个这样的圆锥形零件.
【点评】考查了圆柱与圆锥的体积,解题关键是要读懂题目的意思,根据题目给出的条件,由体积公式找出合适的等量关系列出方程,再求解.
二.点、线、面、体(共6小题)
7.下面图形中,以直线为轴旋转一周,可以得到圆柱体的是( )
A.
B.
C.
D.
【分析】根据面动成体进行解答即可.
【解答】解:A、以直线为轴旋转一周可以得到圆锥,故此选项不合题意;
B、以直线为轴旋转一周可以得到两个圆锥,故此选项不合题意;
C、以直线为轴旋转一周可以得到圆柱,故此选项符合题意;
D、以直线为轴旋转一周可以得到球,故此选项不合题意;
故选:C.
【点评】此题主要考查了点、线、面、体,关键是掌握点动成线,线动成面,面动成体,人是常见几何体.
8.“节日的焰火”可以说是( )
A.面与面交于线
B.点动成线
C.面动成体
D.线动成面
【分析】根据节日的焰火的火的运动路线可知点动即可成线.
【解答】解:根据节日的焰火的火的运动路线,
可以认为节日的焰火的火就是一个点,可知点动即可成线.
故选:B.
【点评】此题主要考查了点、线、面、体的形成,根据题意认为节日的焰火的火就是一个点从而解决问题.
9.将左面的平面图形绕轴旋转一周,得到的立体图形是( )
A.
B.
C.
D.
【分析】根据面动成体,梯形绕上底边旋转是圆柱减圆锥,可得答案.
【解答】解:梯形绕上底边旋转是圆柱减圆锥,故C正确;
故选:C.
【点评】本题考查了点、线、面、体,利用面动成体,直角三角形绕直角边旋转是圆锥,矩形绕边旋转是圆柱.
10.一直角三角形的直角边分别为3和5,以直角边所在的直线为轴旋转一周得到的图形的体积是 15π或25π .
【分析】根据直角三角形绕直角边旋转得圆锥,根据圆锥的体积公式,可得答案.
【解答】解:高为3,半径为5,圆锥的体积是π×52×3=25π;
高为5,半径为3,圆锥的体积是π×32×5=15π;
故答案为:15π或25π.
【点评】本题考查了点线面体,利用直角三角形绕直角边旋转得圆锥是解题的关键,要分类讨论,以防遗漏.
11.笔尖可以看作一个点,这个点在纸上运动时就形成了线,这可以说点动成线;汽车的雨刷在档风玻璃上画出一个扇面,这可以说 线动成面 .
【分析】汽车的雨刷实际上是一条线,通过运动把玻璃上的雨水刷干净,所以应是线动成面.
【解答】解:汽车的雨刷实际上是一条线,通过运动把玻璃上的雨水刷干净,所以应是线动成面.
故答案为:线动成面.
【点评】此题考查了点、线、面、体,正确理解点线面体的概念是解题的关键.
12.小明学习了“面动成体”之后,他用一个边长为3cm、4cm和5cm的直角三角形,其中一条直角边旋转一周,得到了一个几何体,请计算出几何体的体积.(锥体体积=底面积×高)
【分析】根据三角形旋转是圆锥,分旋转轴是3cm和4cm两种情况可得几何体体积.
【解答】解:以4cm为轴体积为×π×32×4=12π,
以3cm为轴的体积为×π×42×3=16π.
【点评】本题考查了点线面体,利用三角形旋转是圆锥是解题关键.
三.认识平面图形(共6小题)
13.一个圆的周长是10π,它的面积是( )
A.25π
B.5π
C.100π
D.10π
【分析】根据圆的周长公式,由已知的周长求出圆的半径,利用圆的面积公式即可求出所求圆的面积.
【解答】解:设圆的半径为r,
∵圆的周长为10π,
∴2πr=10π,即r=5,
则圆的面积S=πr2=25π.
故选:A.
【点评】此题考查了圆的周长公式,以及圆的面积公式,根据周长求出圆的半径是解本题的关键.同时要求学生熟练掌握圆中的有关计算公式.
14.在一个长8厘米,宽7厘米的长方形里面画一个最大的圆,圆规两脚之间的距离是( )厘米.
A.7
B.4
C.3.5
D.3
【分析】根据在长方形里面画一个最大的圆的直径=长方形的宽即可得到结论.
【解答】解:∵在一个长8厘米,宽7厘米的长方形里面画一个最大的圆,
∴这个最大的圆的直径=长方形的宽7厘米,
∴圆规两脚之间的距离是=3.5(厘米),
故选:C.
【点评】本题考查了认识平面图形,正确的理解题意是解题的关键.
15.如图,一个大长方形恰好被分割成四个正方形,则涂色的小正方形面积是整个长方形面积的( )
A.
B.
C.
D.
【分析】设出涂色正方形的边长,表示其面积;再根据各个正方形之间的关系,表示出整个矩形的长、宽,求出面积即可得出答案.
【解答】解:设阴影正方形的边长为x,
则正方形①的边长为x,正方形②的边长为2x,正方形③的边长为3x,
所以,这个长方形的长为3x,高为5x,其面积为3x?5x=15x2,
又涂色正方形的面积为x?x=x2,
因此涂色的小正方形面积是整个长方形面积的,
故选:C.
【点评】考查基本平面图形的特征,通过图形直观,得出边长之间的关系是解决问题的关键.
16.如图:已知小正方形的面积是16平方厘米,则圆的面积是 50.24 平方厘米.
【分析】根据已知条件“小正方形的面积是16平方厘米,”结合图形得到小正方形的边长即为这个圆的半径,这个正方形的面积也是圆的半径的平方,根据圆的面积公式即可得到结论.
【解答】解:因为小正方形的面积是16平方厘米,所以小正方形的边长是4厘米,即圆的半径是4厘米,所以S=πr2=16π(平方厘米)≈50.24(平方厘米).
【点评】本题考查了认识平面图形,正方形和圆的面积的计算,正确的识别图形是解题的关键.
17.如果圆的周长是62.8厘米,那么这个圆的面积是 314 平方厘米.
【分析】根据圆的周长C=2πr和圆的面积公式S=πr2解答即可.
【解答】解:π取近似值3.14,
圆是半径为62.8÷3.14÷2=10(厘米),
S=πr2=3.14×102=314(平方厘米),
所以这个圆的面积是314平方厘米.
故答案为:314.
【点评】本题考查了圆的周长和面积的计算.解答本题的关键是记住圆的周长C=2πr和圆的面积公式S=πr2.
18.有一个著名的希波克拉蒂月牙问题.如图:以AB为直径作半圆,C是圆弧上一点,(不与A、B重合),以AC、BC为直径分别作半圆,围成两个月牙形1、2(阴影部分).已知直径AC为4,直径BC为3,直径AB为5.
(1)分别求出三个半圆的面积(结果保留π);
(2)请你猜测,这两个月牙形的面积与三角形ABC的面积之间有何等量关系,请写出你的猜想,并通过计算说明.
【分析】(1)根据圆的面积公式进行计算即可,
(2)利用面积之间的关系可得两个月牙形的面积之和等于三角形ABC的面积.
【解答】解:(1)以AB为直径的半圆:
SAB为直径=π×()2=π,
以AC为直径的半圆:
SAC为直径=π×22=2π,
以BC为直径的半圆:
SBC为直径=π×()2=π,
∴SAB为直径=SAC为直径+SBC为直径=π,
(2)两个月牙形的面积之和等于三角形ABC的面积.
如图,四个月牙的面积依次为S1,S2,S3,S4,
于是,S1+S2=SBC为直径=π,S3+S4=SBC为直径=2π,
∴S1+S2+S3+S4=SBC为直径+SBC为直径=SAB为直径=S2+S4+S△ABC,
∴S1+S3=S△ABC,
即:两个月牙形的面积之和等于三角形ABC的面积.
【点评】考查圆的面积的计算方法,理清图形中各个部分面积之间的关系是解决问题的关键.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/11
9:50:10;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
