4.3.2 角的比较与运算 同步练习(含解析)
文档属性
| 名称 | 4.3.2 角的比较与运算 同步练习(含解析) | 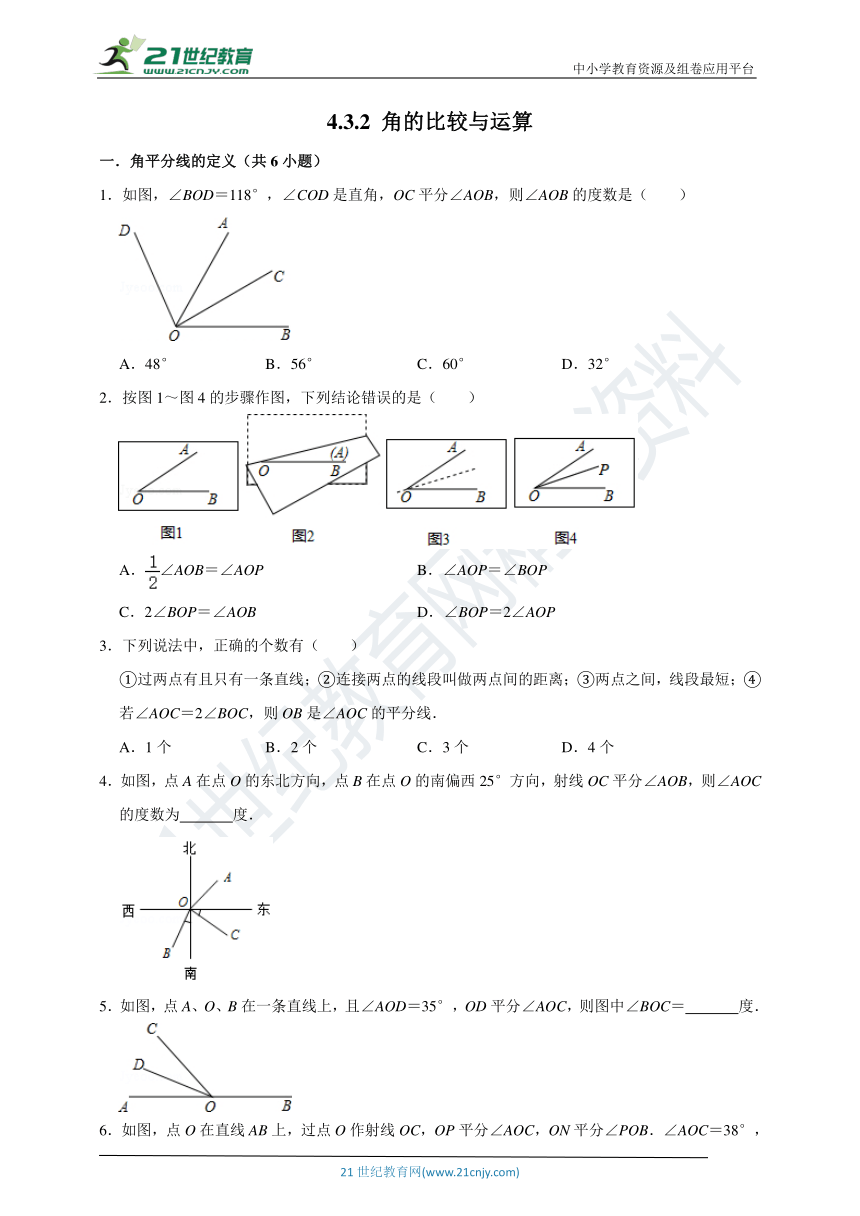 | |
| 格式 | doc | ||
| 文件大小 | 345.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-11 09:20:53 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
4.3.2
角的比较与运算
一.角平分线的定义(共6小题)
1.如图,∠BOD=118°,∠COD是直角,OC平分∠AOB,则∠AOB的度数是( )
A.48°
B.56°
C.60°
D.32°
2.按图1~图4的步骤作图,下列结论错误的是( )
A.∠AOB=∠AOP
B.∠AOP=∠BOP
C.2∠BOP=∠AOB
D.∠BOP=2∠AOP
3.下列说法中,正确的个数有( )
①过两点有且只有一条直线;②连接两点的线段叫做两点间的距离;③两点之间,线段最短;④若∠AOC=2∠BOC,则OB是∠AOC的平分线.
A.1个
B.2个
C.3个
D.4个
4.如图,点A在点O的东北方向,点B在点O的南偏西25°方向,射线OC平分∠AOB,则∠AOC的度数为
度.
5.如图,点A、O、B在一条直线上,且∠AOD=35°,OD平分∠AOC,则图中∠BOC=
度.
6.如图,点O在直线AB上,过点O作射线OC,OP平分∠AOC,ON平分∠POB.∠AOC=38°,求∠CON的度数.
二.角的计算(共6小题)
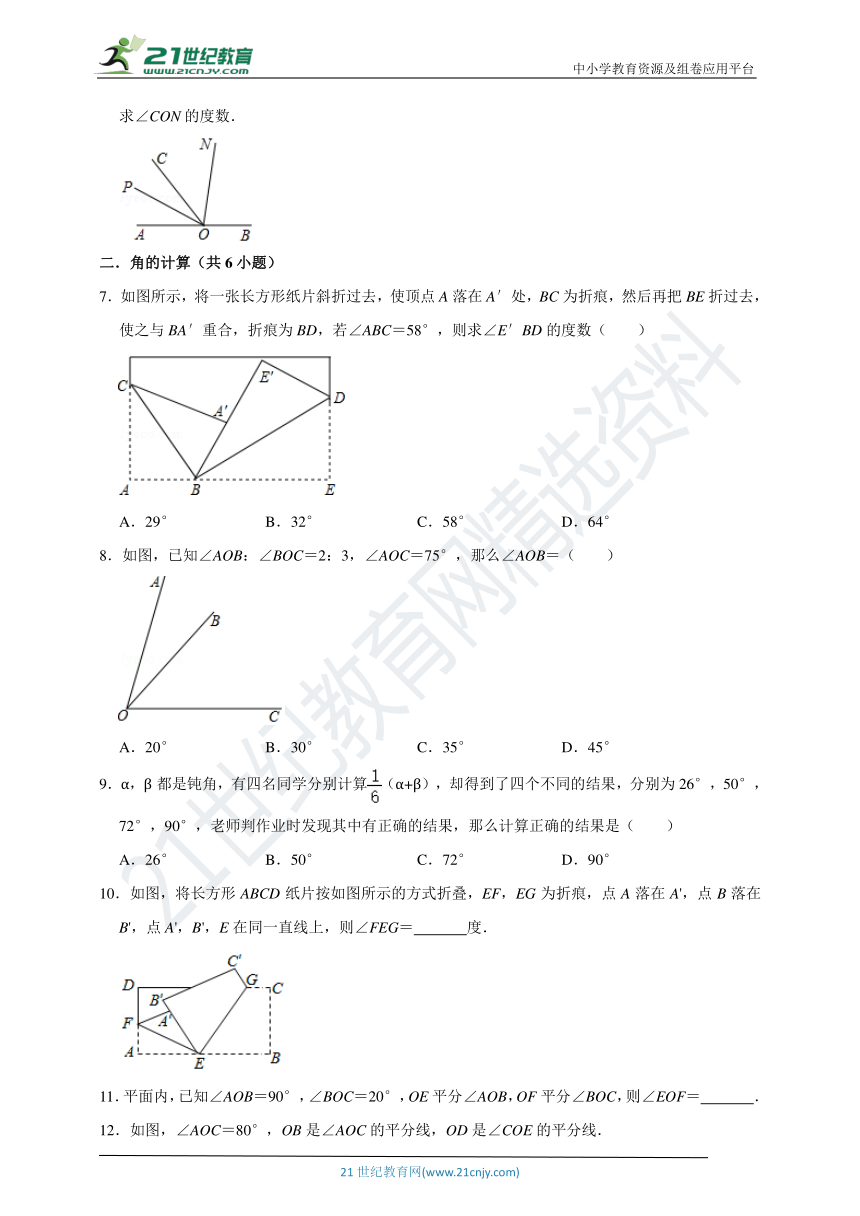
7.如图所示,将一张长方形纸片斜折过去,使顶点A落在A′处,BC为折痕,然后再把BE折过去,使之与BA′重合,折痕为BD,若∠ABC=58°,则求∠E′BD的度数( )
A.29°
B.32°
C.58°
D.64°
8.如图,已知∠AOB:∠BOC=2:3,∠AOC=75°,那么∠AOB=( )
A.20°
B.30°
C.35°
D.45°
9.α,β都是钝角,有四名同学分别计算(α+β),却得到了四个不同的结果,分别为26°,50°,72°,90°,老师判作业时发现其中有正确的结果,那么计算正确的结果是( )
A.26°
B.50°
C.72°
D.90°
10.如图,将长方形ABCD纸片按如图所示的方式折叠,EF,EG为折痕,点A落在A',点B落在B',点A',B',E在同一直线上,则∠FEG=
度.
11.平面内,已知∠AOB=90°,∠BOC=20°,OE平分∠AOB,OF平分∠BOC,则∠EOF=
.
12.如图,∠AOC=80°,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)求∠BOC的度数;
(2)若∠DOE=30°,求∠BOE的度数.
三.角的大小比较(共6小题)
13.将两块相同的直角三角板的顶点重合(如图所示),则∠1与∠2的大小关系是( )
A.∠1>∠2
B.∠1<∠2
C.∠1=∠2
D.以上答案都有可能
14.若∠A=20°18′,∠B=20°15″,∠C=20.25°,则有( )
A.∠A>∠B>∠C
B.∠B>∠A>∠C
C.∠A>∠C>∠B
D.∠C>∠A>∠B
15.已知∠A=18°20′36″,∠B=18.35°,∠C=18°21′,下列比较正确的是( )
A.∠A<∠B
B.∠B<∠A
C.∠B<∠C
D.∠C<∠B
16.比较两个角的大小关系:小明用度量法测得∠AOB=45°,∠COD=50°;小丽用叠合法比较,将两个角的顶点重合,边OB与OD重合,边OA和OC置于重合边的同侧,则边OA
.(填序号:①“在∠COD的内部”;②“在∠COD的外部”;③“与边OC重合”)
17.已知:∠α=40.4°,∠β=40°4′,则∠α
∠β(填“>”、“=”、“<”).
18.如图,AB>AC,AD平分∠BAC,且CD=BD.试说明∠B与∠C的大小关系?
4.3.2
角的比较与运算
参考答案与试题解析
一.角平分线的定义(共6小题)
1.如图,∠BOD=118°,∠COD是直角,OC平分∠AOB,则∠AOB的度数是( )
A.48°
B.56°
C.60°
D.32°
【分析】根据角平分线的定义可知,∠AOB=2∠AOC=2∠BOC,由∠COD是直角可得∠COD=90°,根据已知条件可求∠BOC,进一步得到∠AOB的度数.
【解答】解:∵OC平分∠AOB,
∴∠AOB=2∠AOC=2∠BOC,
∵∠COD是直角,
∴∠COD=90°,
∵∠BOD=118°,
∴∠BOC=∠BOD﹣∠COD=118°﹣90°=28°,
∴∠AOB=2∠BOC=56°.
故选:B.
【点评】本题考查了角平分线的定义,角的计算,解题的关键是熟悉从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.
2.按图1~图4的步骤作图,下列结论错误的是( )
A.∠AOB=∠AOP
B.∠AOP=∠BOP
C.2∠BOP=∠AOB
D.∠BOP=2∠AOP
【分析】根据角平分线的定义对各选项进行逐一分析即可.
【解答】解:∵OP是∠AOB的平分线,
∴∠AOB=2∠AOP=2∠BOP,
∠AOP=∠BOP=∠AOB,
∴选项A、B、C均正确,选项D错误.
故选:D.
【点评】本题考查的是角平分线的定义.解题的关键是掌握角平分线的定义,即从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.
3.下列说法中,正确的个数有( )
①过两点有且只有一条直线;②连接两点的线段叫做两点间的距离;③两点之间,线段最短;④若∠AOC=2∠BOC,则OB是∠AOC的平分线.
A.1个
B.2个
C.3个
D.4个
【分析】根据直线的性质,两点间的距离的定义,线段的性质,角平分线的定义进行分析.
【解答】解:①过两点有且只有一条直线,是直线的公理,故正确;
②连接两点的线段的长度叫两点的距离,故错误;
③两点之间,线段最短,是线段的性质,故正确;
④若OB在∠AOC内部,∠AOC=2∠BOC,OB是∠AOC的平分线,若OB在∠AOC外部则不是,故错误.
故选:B.
【点评】本题考查了直线、线段,角平分线的定义.解题的关键是掌握直线、线段的定义和性质,角平分线的定义.属于基础题.
4.如图,点A在点O的东北方向,点B在点O的南偏西25°方向,射线OC平分∠AOB,则∠AOC的度数为 80 度.
【分析】根据图形,先求出OA与东方的夹角的度数,OB与南方的夹角的度数,再计算∠AOB,最后由角平分线的定义即可得解.
【解答】解:∵点A在点O的东北方向上,
∴OA与东方的夹角为45°,
∵点B在点O的南偏西25°方向上,
∴OA与南方的夹角为25°,
∴∠AOB=45°+90°+25°=160°.
∵射线OC平分∠AOB,
∴∠AOC的度数为:×160°=80°.
故答案为:80.
【点评】本题考查了方向角,是基础题,熟记概念是解题的关键,利用数形结合更形象直观.
5.如图,点A、O、B在一条直线上,且∠AOD=35°,OD平分∠AOC,则图中∠BOC= 110 度.
【分析】利用角平分线的定义和邻补角的定义即可解答.
【解答】解:∵OD平分∠AOC,∠AOD=35°,
∴∠AOC=2∠AOD=2×35°=70°,
∵∠AOC与∠BOC是邻补角,
∴∠AOC+∠BOC=180°,
∴∠BOC=180°﹣70°=110°.
故答案为:110.
【点评】此题考查了角平分线的定义和邻补角的定义,理解角平分线的定义和邻补角的定义是解题的关键.
6.如图,点O在直线AB上,过点O作射线OC,OP平分∠AOC,ON平分∠POB.∠AOC=38°,求∠CON的度数.
【分析】根据OP平分∠AOC,∠AOC=38°可求出∠AOP=19°,进而求出∠BOP,再根据角平分线得出∠PON,最后用角的差求出答案.
【解答】解:∵OP平分∠AOC,∠AOC=38°,
∴∠AOP=∠COP=∠AOC=×38°=19°,
∴∠BOP=180°﹣∠AOP=180°﹣19°=161°,
∵ON平分∠POB
∴∠PON=∠BOP=×161°=80.5°,
∴∠CON=∠PON﹣∠COP=80.5°﹣19°=61.5°.
【点评】考查角平分线的意义,互为补角的意义,理解互补和角平分线的意义是解决问题的前提,利用角度的和或差是解决问题的关键.
二.角的计算(共6小题)
7.如图所示,将一张长方形纸片斜折过去,使顶点A落在A′处,BC为折痕,然后再把BE折过去,使之与BA′重合,折痕为BD,若∠ABC=58°,则求∠E′BD的度数( )
A.29°
B.32°
C.58°
D.64°
【分析】根据折叠得出∠ABC=∠A′BC,∠EBD=∠E′BD,根据∠ABC+∠A′BC+∠EBD+∠E′BD=180°,求出∠ABC+∠E′BD=90°,代入求出即可.
【解答】解:∵根据折叠得出∠ABC=∠A′BC,∠EBD=∠E′BD,
又∵∠ABC+∠A′BC+∠EBD+∠E′BD=180°,
∴∠ABC+∠E′BD=90°,
∵∠ABC=58°,
∴∠E′BD=32°.
故选:B.
【点评】本题考查了角的有关计算和折叠的性质,能根据折叠的性质得出∠ABC=∠A′BC和∠EBD=∠E′BD是解此题的关键.
8.如图,已知∠AOB:∠BOC=2:3,∠AOC=75°,那么∠AOB=( )
A.20°
B.30°
C.35°
D.45°
【分析】由∠AOB:∠BOC=2:3,可得∠AOB=∠AOC进而求出答案,做出选择.
【解答】解:∵∠AOB:∠BOC=2:3,∠AOC=75°,
∴∠AOB=∠AOC=×75°=30°,
故选:B.
【点评】本题考查角的有关计算,按比例分配转化为∠AOB=∠AOC是解答的关键.
9.α,β都是钝角,有四名同学分别计算(α+β),却得到了四个不同的结果,分别为26°,50°,72°,90°,老师判作业时发现其中有正确的结果,那么计算正确的结果是( )
A.26°
B.50°
C.72°
D.90°
【分析】根据钝角的取值范围,得到两个钝角和的取值范围,除以6后看所给的哪个角在这个范围内即可.
【解答】解:∵α、β都是钝角,
∴90°<α<180°,90°<β<180°,
∴180°<α+β<360°,
∴30°<(α+β)<60°,
∴计算正确的结果是50°.
故选:B.
【点评】本题考查了角的有关计算问题.解题的关键是求(α+β)的范围.
10.如图,将长方形ABCD纸片按如图所示的方式折叠,EF,EG为折痕,点A落在A',点B落在B',点A',B',E在同一直线上,则∠FEG= 90 度.
【分析】由折叠可得∠AEF=∠A'EF,∠BEG=∠B'EG,再结合平角的定义可求解∠FEG的度数.
【解答】解:由折叠可得∠AEF=∠A'EF,∠BEG=∠B'EG,
∵∠AEB=180°,
∴∠FEG=∠A'EF+∠B'EG=∠AEB=90°,
故答案为90.
【点评】本题主要考查翻折问题,平角的定义,找到翻折中的隐含条件是解题的关键.
11.平面内,已知∠AOB=90°,∠BOC=20°,OE平分∠AOB,OF平分∠BOC,则∠EOF= 35°或55° .
【分析】分两种情况:当OC在∠AOB内时;当OC在∠AOB外时.根据角平分线的定义,角的和差进行解答便可.
【解答】解:当OC在∠AOB内时,如图1,
∠EOF=∠BOE﹣∠BOF=;
当OC在∠AOB外时,如图2,
∠EOF=∠BOE+∠BOF=,
故答案为:35°或55°.
【点评】本题主要考查了角的和差,角平分线的定义,关键是分情况讨论.
12.如图,∠AOC=80°,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)求∠BOC的度数;
(2)若∠DOE=30°,求∠BOE的度数.
【分析】(1)根据角平分线定义得出∠BOC=∠AOC,代入求出即可;
(2)根据角平分线定义求出∠BOC和∠COE,再代入∠BOE=∠BOC+∠COE求出即可.
【解答】解:(1)∵∠AOC=80°,OB是∠AOC的平分线,
∴∠BOC=∠AOC=×80°=40°;
(2)∵OB是∠AOC的平分线,OD是∠COE的平分线,∠AOC=80°,∠DOE=30°,
∴∠BOC=∠AOC=40°,∠COE=2∠DOE=60°,
∴∠BOE=∠BOC+∠COE=40°+60°=100°.
【点评】本题考查了角平分线定义和角的计算,解题的关键是求出∠BOC、∠COE的度数和得出∠BOE=∠BOC+∠COE.
三.角的大小比较(共6小题)
13.将两块相同的直角三角板的顶点重合(如图所示),则∠1与∠2的大小关系是( )
A.∠1>∠2
B.∠1<∠2
C.∠1=∠2
D.以上答案都有可能
【分析】利用同角的余角相等得出答案.
【解答】解:∵∠1+∠BOC=∠AOC=90°,∠2+∠BOC=∠BOD=90°,
∴∠1=∠2,
故选:C.
【点评】考查互为余角的意义,掌握同角的余角相等是正确判断的前提.
14.若∠A=20°18′,∠B=20°15″,∠C=20.25°,则有( )
A.∠A>∠B>∠C
B.∠B>∠A>∠C
C.∠A>∠C>∠B
D.∠C>∠A>∠B
【分析】根据度分秒之间的换算,先把∠C的度数化成度、分、秒的形式,再根据角的大小比较的法则进行比较,即可得出答案.
【解答】解:∵∠A=20°18′,∠B=20°15″,
∴∠A>∠B,
∵∠C=20.25°=20°15′,
∴∠B<∠C<∠A,
∴∠A>∠C>∠B.
故选:C.
【点评】此题考查了角的大小比较,先把∠C的度数化成度、分、秒的形式,再进行比较是本题的关键.
15.已知∠A=18°20′36″,∠B=18.35°,∠C=18°21′,下列比较正确的是( )
A.∠A<∠B
B.∠B<∠A
C.∠B<∠C
D.∠C<∠B
【分析】依据∠A=18°20′36″,∠B=18.35°=18°21′,∠C=18°21′,即可得到三个角的大小关系.
【解答】解:∵∠A=18°20′36″,∠B=18.35°=18°21′,∠C=18°21′,
∴∠A<∠B=∠C.
故选:A.
【点评】本题主要考查了角的大小的比较,掌握度分秒的换算是解决问题的关键.
16.比较两个角的大小关系:小明用度量法测得∠AOB=45°,∠COD=50°;小丽用叠合法比较,将两个角的顶点重合,边OB与OD重合,边OA和OC置于重合边的同侧,则边OA ① .(填序号:①“在∠COD的内部”;②“在∠COD的外部”;③“与边OC重合”)
【分析】根据题意画出图形,由∠AOB<∠COD,图形直观得出答案.
【解答】解:如图,由于∠AOB<∠COD,因此OA在∠COD的内部,
故答案为:①;
【点评】考查角的大小比较的方法,度量法、叠合法是常用的方法,叠合法的前提是使两个角的一条边重合,两个角的另一条边都在重合边的同侧.
17.已知:∠α=40.4°,∠β=40°4′,则∠α > ∠β(填“>”、“=”、“<”).
【分析】首先同一单位,利用1°=60′,把∠α=40.4°=40°24′,再进一步与∠β比较得出答案即可.
【解答】解:∵∠α=40.4°=40°24′,∠β=40°4′,
∴∠α>∠β.
故答案是:>.
【点评】此题考查角的大小比较的方法和度分秒之间的换算.在比较角的大小时有时可把度化为分来进行比较.
18.如图,AB>AC,AD平分∠BAC,且CD=BD.试说明∠B与∠C的大小关系?
【分析】在AB上截取AE=AC,连接DE,证△ACD≌△AED,根据全等三角形的性质和等腰三角形的性质即可得到两角的大小关系.
【解答】解:∠B十∠C=180°.
理由如下:在AB上截取AE=AC,连接DE.
∵AD平分∠BAC,
∴∠CAD=∠EAD,
在△ACD与△AED中,
,
∴△ACD≌△AED(SAS),
∴∠C=∠AED,CD=DE,
又∵CD=BD,
∴DE=DB,
∴∠B=∠DEB,
又∵∠DEB+∠AED=180°,
∴∠B+∠C=180°.
【点评】本题主要考查全等三角形的性质和等腰三角形的性质和角平分线的定义.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/13
9:34:38;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
4.3.2
角的比较与运算
一.角平分线的定义(共6小题)
1.如图,∠BOD=118°,∠COD是直角,OC平分∠AOB,则∠AOB的度数是( )
A.48°
B.56°
C.60°
D.32°
2.按图1~图4的步骤作图,下列结论错误的是( )
A.∠AOB=∠AOP
B.∠AOP=∠BOP
C.2∠BOP=∠AOB
D.∠BOP=2∠AOP
3.下列说法中,正确的个数有( )
①过两点有且只有一条直线;②连接两点的线段叫做两点间的距离;③两点之间,线段最短;④若∠AOC=2∠BOC,则OB是∠AOC的平分线.
A.1个
B.2个
C.3个
D.4个
4.如图,点A在点O的东北方向,点B在点O的南偏西25°方向,射线OC平分∠AOB,则∠AOC的度数为
度.
5.如图,点A、O、B在一条直线上,且∠AOD=35°,OD平分∠AOC,则图中∠BOC=
度.
6.如图,点O在直线AB上,过点O作射线OC,OP平分∠AOC,ON平分∠POB.∠AOC=38°,求∠CON的度数.
二.角的计算(共6小题)
7.如图所示,将一张长方形纸片斜折过去,使顶点A落在A′处,BC为折痕,然后再把BE折过去,使之与BA′重合,折痕为BD,若∠ABC=58°,则求∠E′BD的度数( )
A.29°
B.32°
C.58°
D.64°
8.如图,已知∠AOB:∠BOC=2:3,∠AOC=75°,那么∠AOB=( )
A.20°
B.30°
C.35°
D.45°
9.α,β都是钝角,有四名同学分别计算(α+β),却得到了四个不同的结果,分别为26°,50°,72°,90°,老师判作业时发现其中有正确的结果,那么计算正确的结果是( )
A.26°
B.50°
C.72°
D.90°
10.如图,将长方形ABCD纸片按如图所示的方式折叠,EF,EG为折痕,点A落在A',点B落在B',点A',B',E在同一直线上,则∠FEG=
度.
11.平面内,已知∠AOB=90°,∠BOC=20°,OE平分∠AOB,OF平分∠BOC,则∠EOF=
.
12.如图,∠AOC=80°,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)求∠BOC的度数;
(2)若∠DOE=30°,求∠BOE的度数.
三.角的大小比较(共6小题)
13.将两块相同的直角三角板的顶点重合(如图所示),则∠1与∠2的大小关系是( )
A.∠1>∠2
B.∠1<∠2
C.∠1=∠2
D.以上答案都有可能
14.若∠A=20°18′,∠B=20°15″,∠C=20.25°,则有( )
A.∠A>∠B>∠C
B.∠B>∠A>∠C
C.∠A>∠C>∠B
D.∠C>∠A>∠B
15.已知∠A=18°20′36″,∠B=18.35°,∠C=18°21′,下列比较正确的是( )
A.∠A<∠B
B.∠B<∠A
C.∠B<∠C
D.∠C<∠B
16.比较两个角的大小关系:小明用度量法测得∠AOB=45°,∠COD=50°;小丽用叠合法比较,将两个角的顶点重合,边OB与OD重合,边OA和OC置于重合边的同侧,则边OA
.(填序号:①“在∠COD的内部”;②“在∠COD的外部”;③“与边OC重合”)
17.已知:∠α=40.4°,∠β=40°4′,则∠α
∠β(填“>”、“=”、“<”).
18.如图,AB>AC,AD平分∠BAC,且CD=BD.试说明∠B与∠C的大小关系?
4.3.2
角的比较与运算
参考答案与试题解析
一.角平分线的定义(共6小题)
1.如图,∠BOD=118°,∠COD是直角,OC平分∠AOB,则∠AOB的度数是( )
A.48°
B.56°
C.60°
D.32°
【分析】根据角平分线的定义可知,∠AOB=2∠AOC=2∠BOC,由∠COD是直角可得∠COD=90°,根据已知条件可求∠BOC,进一步得到∠AOB的度数.
【解答】解:∵OC平分∠AOB,
∴∠AOB=2∠AOC=2∠BOC,
∵∠COD是直角,
∴∠COD=90°,
∵∠BOD=118°,
∴∠BOC=∠BOD﹣∠COD=118°﹣90°=28°,
∴∠AOB=2∠BOC=56°.
故选:B.
【点评】本题考查了角平分线的定义,角的计算,解题的关键是熟悉从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.
2.按图1~图4的步骤作图,下列结论错误的是( )
A.∠AOB=∠AOP
B.∠AOP=∠BOP
C.2∠BOP=∠AOB
D.∠BOP=2∠AOP
【分析】根据角平分线的定义对各选项进行逐一分析即可.
【解答】解:∵OP是∠AOB的平分线,
∴∠AOB=2∠AOP=2∠BOP,
∠AOP=∠BOP=∠AOB,
∴选项A、B、C均正确,选项D错误.
故选:D.
【点评】本题考查的是角平分线的定义.解题的关键是掌握角平分线的定义,即从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.
3.下列说法中,正确的个数有( )
①过两点有且只有一条直线;②连接两点的线段叫做两点间的距离;③两点之间,线段最短;④若∠AOC=2∠BOC,则OB是∠AOC的平分线.
A.1个
B.2个
C.3个
D.4个
【分析】根据直线的性质,两点间的距离的定义,线段的性质,角平分线的定义进行分析.
【解答】解:①过两点有且只有一条直线,是直线的公理,故正确;
②连接两点的线段的长度叫两点的距离,故错误;
③两点之间,线段最短,是线段的性质,故正确;
④若OB在∠AOC内部,∠AOC=2∠BOC,OB是∠AOC的平分线,若OB在∠AOC外部则不是,故错误.
故选:B.
【点评】本题考查了直线、线段,角平分线的定义.解题的关键是掌握直线、线段的定义和性质,角平分线的定义.属于基础题.
4.如图,点A在点O的东北方向,点B在点O的南偏西25°方向,射线OC平分∠AOB,则∠AOC的度数为 80 度.
【分析】根据图形,先求出OA与东方的夹角的度数,OB与南方的夹角的度数,再计算∠AOB,最后由角平分线的定义即可得解.
【解答】解:∵点A在点O的东北方向上,
∴OA与东方的夹角为45°,
∵点B在点O的南偏西25°方向上,
∴OA与南方的夹角为25°,
∴∠AOB=45°+90°+25°=160°.
∵射线OC平分∠AOB,
∴∠AOC的度数为:×160°=80°.
故答案为:80.
【点评】本题考查了方向角,是基础题,熟记概念是解题的关键,利用数形结合更形象直观.
5.如图,点A、O、B在一条直线上,且∠AOD=35°,OD平分∠AOC,则图中∠BOC= 110 度.
【分析】利用角平分线的定义和邻补角的定义即可解答.
【解答】解:∵OD平分∠AOC,∠AOD=35°,
∴∠AOC=2∠AOD=2×35°=70°,
∵∠AOC与∠BOC是邻补角,
∴∠AOC+∠BOC=180°,
∴∠BOC=180°﹣70°=110°.
故答案为:110.
【点评】此题考查了角平分线的定义和邻补角的定义,理解角平分线的定义和邻补角的定义是解题的关键.
6.如图,点O在直线AB上,过点O作射线OC,OP平分∠AOC,ON平分∠POB.∠AOC=38°,求∠CON的度数.
【分析】根据OP平分∠AOC,∠AOC=38°可求出∠AOP=19°,进而求出∠BOP,再根据角平分线得出∠PON,最后用角的差求出答案.
【解答】解:∵OP平分∠AOC,∠AOC=38°,
∴∠AOP=∠COP=∠AOC=×38°=19°,
∴∠BOP=180°﹣∠AOP=180°﹣19°=161°,
∵ON平分∠POB
∴∠PON=∠BOP=×161°=80.5°,
∴∠CON=∠PON﹣∠COP=80.5°﹣19°=61.5°.
【点评】考查角平分线的意义,互为补角的意义,理解互补和角平分线的意义是解决问题的前提,利用角度的和或差是解决问题的关键.
二.角的计算(共6小题)
7.如图所示,将一张长方形纸片斜折过去,使顶点A落在A′处,BC为折痕,然后再把BE折过去,使之与BA′重合,折痕为BD,若∠ABC=58°,则求∠E′BD的度数( )
A.29°
B.32°
C.58°
D.64°
【分析】根据折叠得出∠ABC=∠A′BC,∠EBD=∠E′BD,根据∠ABC+∠A′BC+∠EBD+∠E′BD=180°,求出∠ABC+∠E′BD=90°,代入求出即可.
【解答】解:∵根据折叠得出∠ABC=∠A′BC,∠EBD=∠E′BD,
又∵∠ABC+∠A′BC+∠EBD+∠E′BD=180°,
∴∠ABC+∠E′BD=90°,
∵∠ABC=58°,
∴∠E′BD=32°.
故选:B.
【点评】本题考查了角的有关计算和折叠的性质,能根据折叠的性质得出∠ABC=∠A′BC和∠EBD=∠E′BD是解此题的关键.
8.如图,已知∠AOB:∠BOC=2:3,∠AOC=75°,那么∠AOB=( )
A.20°
B.30°
C.35°
D.45°
【分析】由∠AOB:∠BOC=2:3,可得∠AOB=∠AOC进而求出答案,做出选择.
【解答】解:∵∠AOB:∠BOC=2:3,∠AOC=75°,
∴∠AOB=∠AOC=×75°=30°,
故选:B.
【点评】本题考查角的有关计算,按比例分配转化为∠AOB=∠AOC是解答的关键.
9.α,β都是钝角,有四名同学分别计算(α+β),却得到了四个不同的结果,分别为26°,50°,72°,90°,老师判作业时发现其中有正确的结果,那么计算正确的结果是( )
A.26°
B.50°
C.72°
D.90°
【分析】根据钝角的取值范围,得到两个钝角和的取值范围,除以6后看所给的哪个角在这个范围内即可.
【解答】解:∵α、β都是钝角,
∴90°<α<180°,90°<β<180°,
∴180°<α+β<360°,
∴30°<(α+β)<60°,
∴计算正确的结果是50°.
故选:B.
【点评】本题考查了角的有关计算问题.解题的关键是求(α+β)的范围.
10.如图,将长方形ABCD纸片按如图所示的方式折叠,EF,EG为折痕,点A落在A',点B落在B',点A',B',E在同一直线上,则∠FEG= 90 度.
【分析】由折叠可得∠AEF=∠A'EF,∠BEG=∠B'EG,再结合平角的定义可求解∠FEG的度数.
【解答】解:由折叠可得∠AEF=∠A'EF,∠BEG=∠B'EG,
∵∠AEB=180°,
∴∠FEG=∠A'EF+∠B'EG=∠AEB=90°,
故答案为90.
【点评】本题主要考查翻折问题,平角的定义,找到翻折中的隐含条件是解题的关键.
11.平面内,已知∠AOB=90°,∠BOC=20°,OE平分∠AOB,OF平分∠BOC,则∠EOF= 35°或55° .
【分析】分两种情况:当OC在∠AOB内时;当OC在∠AOB外时.根据角平分线的定义,角的和差进行解答便可.
【解答】解:当OC在∠AOB内时,如图1,
∠EOF=∠BOE﹣∠BOF=;
当OC在∠AOB外时,如图2,
∠EOF=∠BOE+∠BOF=,
故答案为:35°或55°.
【点评】本题主要考查了角的和差,角平分线的定义,关键是分情况讨论.
12.如图,∠AOC=80°,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)求∠BOC的度数;
(2)若∠DOE=30°,求∠BOE的度数.
【分析】(1)根据角平分线定义得出∠BOC=∠AOC,代入求出即可;
(2)根据角平分线定义求出∠BOC和∠COE,再代入∠BOE=∠BOC+∠COE求出即可.
【解答】解:(1)∵∠AOC=80°,OB是∠AOC的平分线,
∴∠BOC=∠AOC=×80°=40°;
(2)∵OB是∠AOC的平分线,OD是∠COE的平分线,∠AOC=80°,∠DOE=30°,
∴∠BOC=∠AOC=40°,∠COE=2∠DOE=60°,
∴∠BOE=∠BOC+∠COE=40°+60°=100°.
【点评】本题考查了角平分线定义和角的计算,解题的关键是求出∠BOC、∠COE的度数和得出∠BOE=∠BOC+∠COE.
三.角的大小比较(共6小题)
13.将两块相同的直角三角板的顶点重合(如图所示),则∠1与∠2的大小关系是( )
A.∠1>∠2
B.∠1<∠2
C.∠1=∠2
D.以上答案都有可能
【分析】利用同角的余角相等得出答案.
【解答】解:∵∠1+∠BOC=∠AOC=90°,∠2+∠BOC=∠BOD=90°,
∴∠1=∠2,
故选:C.
【点评】考查互为余角的意义,掌握同角的余角相等是正确判断的前提.
14.若∠A=20°18′,∠B=20°15″,∠C=20.25°,则有( )
A.∠A>∠B>∠C
B.∠B>∠A>∠C
C.∠A>∠C>∠B
D.∠C>∠A>∠B
【分析】根据度分秒之间的换算,先把∠C的度数化成度、分、秒的形式,再根据角的大小比较的法则进行比较,即可得出答案.
【解答】解:∵∠A=20°18′,∠B=20°15″,
∴∠A>∠B,
∵∠C=20.25°=20°15′,
∴∠B<∠C<∠A,
∴∠A>∠C>∠B.
故选:C.
【点评】此题考查了角的大小比较,先把∠C的度数化成度、分、秒的形式,再进行比较是本题的关键.
15.已知∠A=18°20′36″,∠B=18.35°,∠C=18°21′,下列比较正确的是( )
A.∠A<∠B
B.∠B<∠A
C.∠B<∠C
D.∠C<∠B
【分析】依据∠A=18°20′36″,∠B=18.35°=18°21′,∠C=18°21′,即可得到三个角的大小关系.
【解答】解:∵∠A=18°20′36″,∠B=18.35°=18°21′,∠C=18°21′,
∴∠A<∠B=∠C.
故选:A.
【点评】本题主要考查了角的大小的比较,掌握度分秒的换算是解决问题的关键.
16.比较两个角的大小关系:小明用度量法测得∠AOB=45°,∠COD=50°;小丽用叠合法比较,将两个角的顶点重合,边OB与OD重合,边OA和OC置于重合边的同侧,则边OA ① .(填序号:①“在∠COD的内部”;②“在∠COD的外部”;③“与边OC重合”)
【分析】根据题意画出图形,由∠AOB<∠COD,图形直观得出答案.
【解答】解:如图,由于∠AOB<∠COD,因此OA在∠COD的内部,
故答案为:①;
【点评】考查角的大小比较的方法,度量法、叠合法是常用的方法,叠合法的前提是使两个角的一条边重合,两个角的另一条边都在重合边的同侧.
17.已知:∠α=40.4°,∠β=40°4′,则∠α > ∠β(填“>”、“=”、“<”).
【分析】首先同一单位,利用1°=60′,把∠α=40.4°=40°24′,再进一步与∠β比较得出答案即可.
【解答】解:∵∠α=40.4°=40°24′,∠β=40°4′,
∴∠α>∠β.
故答案是:>.
【点评】此题考查角的大小比较的方法和度分秒之间的换算.在比较角的大小时有时可把度化为分来进行比较.
18.如图,AB>AC,AD平分∠BAC,且CD=BD.试说明∠B与∠C的大小关系?
【分析】在AB上截取AE=AC,连接DE,证△ACD≌△AED,根据全等三角形的性质和等腰三角形的性质即可得到两角的大小关系.
【解答】解:∠B十∠C=180°.
理由如下:在AB上截取AE=AC,连接DE.
∵AD平分∠BAC,
∴∠CAD=∠EAD,
在△ACD与△AED中,
,
∴△ACD≌△AED(SAS),
∴∠C=∠AED,CD=DE,
又∵CD=BD,
∴DE=DB,
∴∠B=∠DEB,
又∵∠DEB+∠AED=180°,
∴∠B+∠C=180°.
【点评】本题主要考查全等三角形的性质和等腰三角形的性质和角平分线的定义.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/13
9:34:38;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
