4.3.3 余角和补角 同步练习(含解析)
文档属性
| 名称 | 4.3.3 余角和补角 同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 197.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-11 09:23:08 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
4.3.3
余角和补角
一.余角和补角(共6小题)
1.下列说法中,正确的是( )
①已知∠A=40°,则∠A的余角是50°.
②若∠1+∠2=90°,则∠1和∠2互为余角.
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3互为补角.
④一个角的补角必为钝角.
A.①,②
B.①,②,③
C.③,④,②
D.③,④
2.如果一个角的补角是125°,那么这个角的余角的度数是( )
A.55°
B.50°
C.35°
D.110°
3.如图,将一副三角尺按下列位置摆放,使∠α和∠β互余的摆放方式是( )
A.
B.
C.
D.
4.若一个角的补角是108°,则这个角的余角是
度.
5.将两个三角尺的直角顶点重合为如图所示的位置,若∠AOD=108°,则∠COB=
.
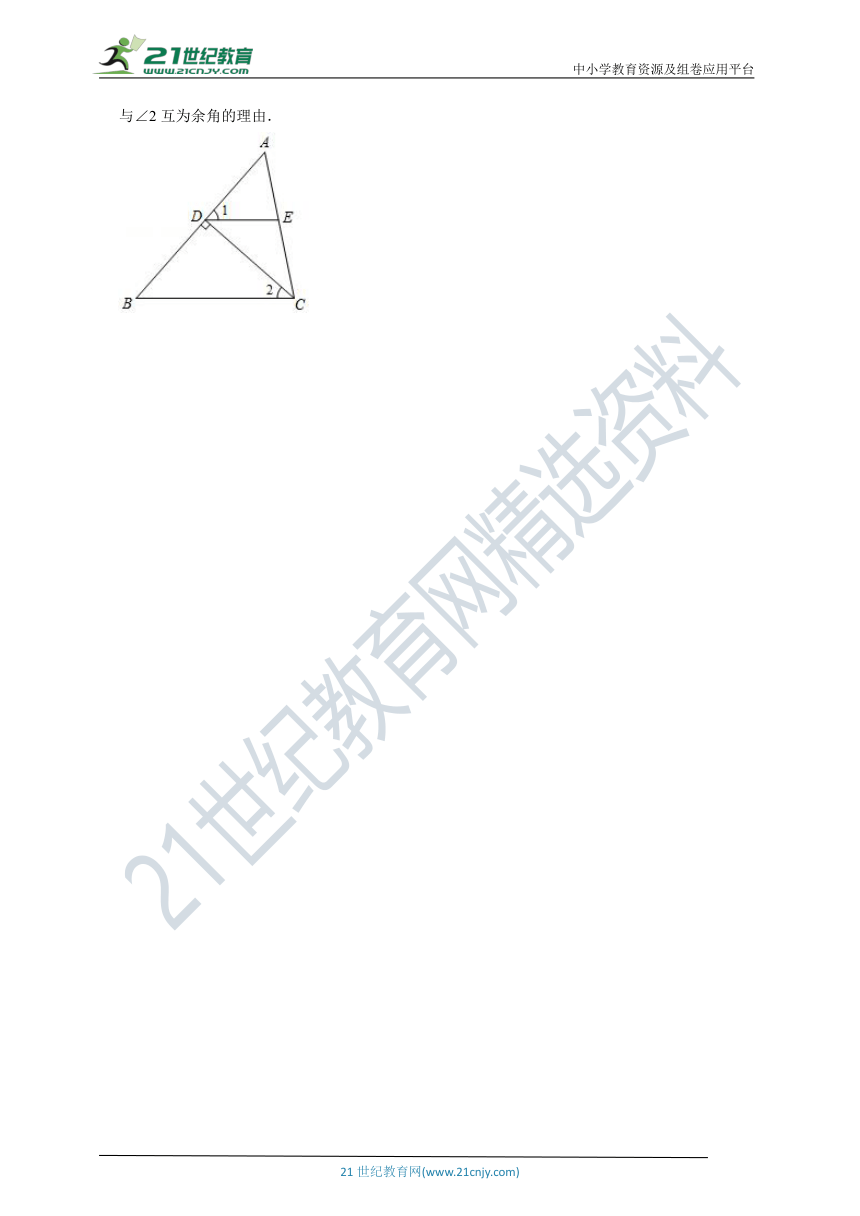
6.如图,在三角形ABC中,CD⊥AB于点D,点E在边AC上,且∠AED=∠ACB.请你说明∠1与∠2互为余角的理由.
4.3.3
余角和补角
参考答案与试题解析
一.余角和补角(共6小题)
1.下列说法中,正确的是( )
①已知∠A=40°,则∠A的余角是50°.
②若∠1+∠2=90°,则∠1和∠2互为余角.
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3互为补角.
④一个角的补角必为钝角.
A.①,②
B.①,②,③
C.③,④,②
D.③,④
【分析】根据补角和余角的概念解答,和为180度的两个角互为补角;和为90度的两个角互为余角.
【解答】解:①已知∠A=40°,则∠A的余角是50°,原说法正确;
②若∠1+∠2=90°,则∠1和∠2互为余角,原说法正确;
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3不能互为补角,原说法错误;
④一个角的补角不一定是钝角,原说法错误.
说法正确的是①②,
故选:A.
【点评】本题考查了补角和余角的概念.解题的关键是记住互为余角的两个角的和为90°;两个角互为补角和为180°.
2.如果一个角的补角是125°,那么这个角的余角的度数是( )
A.55°
B.50°
C.35°
D.110°
【分析】根据余角和补角的定义,即可解答.
【解答】解:∵一个角的补角是125°,
∴这个角为:180°﹣125°=55°,
∴这个角的余角为:90°﹣55°=35°,
故选:C.
【点评】本题考查了余角和补角的定义,解决本题的关键是熟记余角和补角的定义.
3.如图,将一副三角尺按下列位置摆放,使∠α和∠β互余的摆放方式是( )
A.
B.
C.
D.
【分析】根据余角和补角的概念、结合图形进行判断即可.
【解答】解:A.∠α与∠β互余,故本选项正确;
B.∠α=∠β,故本选项错误;
C.∠α=∠β,故本选项错误;
D.∠α与∠β互补,故本选项错误,
故选:A.
【点评】本题考查了余角和补角,是基础题,熟记概念与性质是解题的关键.
4.若一个角的补角是108°,则这个角的余角是 18 度.
【分析】一个角的补角比这个角的余角大90°,根据以上内容得出即可.
【解答】解:∵一个角的补角是108°,
∴这个角的余角是108°﹣90°=18°,
故答案为:18.
【点评】本题考查了补角和余角,能熟记补角和余角的定义是解此题的关键,注意:∠A的补角是180°﹣∠A,∠A的余角是90°﹣∠A.
5.将两个三角尺的直角顶点重合为如图所示的位置,若∠AOD=108°,则∠COB= 72° .
【分析】根据∠COD=90°,∠AOD=108°,进而得出∠AOC的度数,根据∠COB=∠AOB﹣∠AOC即可得出结论.
【解答】解:∵∠COD=90°,∠AOB=90°,∠AOD=108°,
∴∠AOC=∠AOD﹣∠COD=108°﹣90°=18°,
∴∠COB=∠AOB﹣∠AOC=90°﹣18°=72°.
故答案为:72°.
【点评】本题考查了角的计算及直角三角形,熟知角的和差计算方法是解答此题的关键.
6.如图,在三角形ABC中,CD⊥AB于点D,点E在边AC上,且∠AED=∠ACB.请你说明∠1与∠2互为余角的理由.
【分析】根据平行线的判定与性质可得∠2=∠EDC,再根据垂直结合余角的定义可求解.
【解答】解:∵∠AED=∠ACB,
∴DE∥BC,
∴∠2=∠EDC,
∵CD⊥AB,
∴∠1+∠EDC=90°,
∴∠1+∠2=180°,
故∠1与∠2互余.
【点评】本题主要考查余角的定义,平行线的性质与判定,垂直的定义,判定∠2=∠EDC是解题的关键.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/13
9:35:46;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
4.3.3
余角和补角
一.余角和补角(共6小题)
1.下列说法中,正确的是( )
①已知∠A=40°,则∠A的余角是50°.
②若∠1+∠2=90°,则∠1和∠2互为余角.
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3互为补角.
④一个角的补角必为钝角.
A.①,②
B.①,②,③
C.③,④,②
D.③,④
2.如果一个角的补角是125°,那么这个角的余角的度数是( )
A.55°
B.50°
C.35°
D.110°
3.如图,将一副三角尺按下列位置摆放,使∠α和∠β互余的摆放方式是( )
A.
B.
C.
D.
4.若一个角的补角是108°,则这个角的余角是
度.
5.将两个三角尺的直角顶点重合为如图所示的位置,若∠AOD=108°,则∠COB=
.
6.如图,在三角形ABC中,CD⊥AB于点D,点E在边AC上,且∠AED=∠ACB.请你说明∠1与∠2互为余角的理由.
4.3.3
余角和补角
参考答案与试题解析
一.余角和补角(共6小题)
1.下列说法中,正确的是( )
①已知∠A=40°,则∠A的余角是50°.
②若∠1+∠2=90°,则∠1和∠2互为余角.
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3互为补角.
④一个角的补角必为钝角.
A.①,②
B.①,②,③
C.③,④,②
D.③,④
【分析】根据补角和余角的概念解答,和为180度的两个角互为补角;和为90度的两个角互为余角.
【解答】解:①已知∠A=40°,则∠A的余角是50°,原说法正确;
②若∠1+∠2=90°,则∠1和∠2互为余角,原说法正确;
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3不能互为补角,原说法错误;
④一个角的补角不一定是钝角,原说法错误.
说法正确的是①②,
故选:A.
【点评】本题考查了补角和余角的概念.解题的关键是记住互为余角的两个角的和为90°;两个角互为补角和为180°.
2.如果一个角的补角是125°,那么这个角的余角的度数是( )
A.55°
B.50°
C.35°
D.110°
【分析】根据余角和补角的定义,即可解答.
【解答】解:∵一个角的补角是125°,
∴这个角为:180°﹣125°=55°,
∴这个角的余角为:90°﹣55°=35°,
故选:C.
【点评】本题考查了余角和补角的定义,解决本题的关键是熟记余角和补角的定义.
3.如图,将一副三角尺按下列位置摆放,使∠α和∠β互余的摆放方式是( )
A.
B.
C.
D.
【分析】根据余角和补角的概念、结合图形进行判断即可.
【解答】解:A.∠α与∠β互余,故本选项正确;
B.∠α=∠β,故本选项错误;
C.∠α=∠β,故本选项错误;
D.∠α与∠β互补,故本选项错误,
故选:A.
【点评】本题考查了余角和补角,是基础题,熟记概念与性质是解题的关键.
4.若一个角的补角是108°,则这个角的余角是 18 度.
【分析】一个角的补角比这个角的余角大90°,根据以上内容得出即可.
【解答】解:∵一个角的补角是108°,
∴这个角的余角是108°﹣90°=18°,
故答案为:18.
【点评】本题考查了补角和余角,能熟记补角和余角的定义是解此题的关键,注意:∠A的补角是180°﹣∠A,∠A的余角是90°﹣∠A.
5.将两个三角尺的直角顶点重合为如图所示的位置,若∠AOD=108°,则∠COB= 72° .
【分析】根据∠COD=90°,∠AOD=108°,进而得出∠AOC的度数,根据∠COB=∠AOB﹣∠AOC即可得出结论.
【解答】解:∵∠COD=90°,∠AOB=90°,∠AOD=108°,
∴∠AOC=∠AOD﹣∠COD=108°﹣90°=18°,
∴∠COB=∠AOB﹣∠AOC=90°﹣18°=72°.
故答案为:72°.
【点评】本题考查了角的计算及直角三角形,熟知角的和差计算方法是解答此题的关键.
6.如图,在三角形ABC中,CD⊥AB于点D,点E在边AC上,且∠AED=∠ACB.请你说明∠1与∠2互为余角的理由.
【分析】根据平行线的判定与性质可得∠2=∠EDC,再根据垂直结合余角的定义可求解.
【解答】解:∵∠AED=∠ACB,
∴DE∥BC,
∴∠2=∠EDC,
∵CD⊥AB,
∴∠1+∠EDC=90°,
∴∠1+∠2=180°,
故∠1与∠2互余.
【点评】本题主要考查余角的定义,平行线的性质与判定,垂直的定义,判定∠2=∠EDC是解题的关键.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/13
9:35:46;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
