4.4 课题学习 设计制作长方体形 同步练习(含解析)
文档属性
| 名称 | 4.4 课题学习 设计制作长方体形 同步练习(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 299.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-11 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
4.4
课题学习
设计制作长方体形
一.几何体的展开图(共6小题)
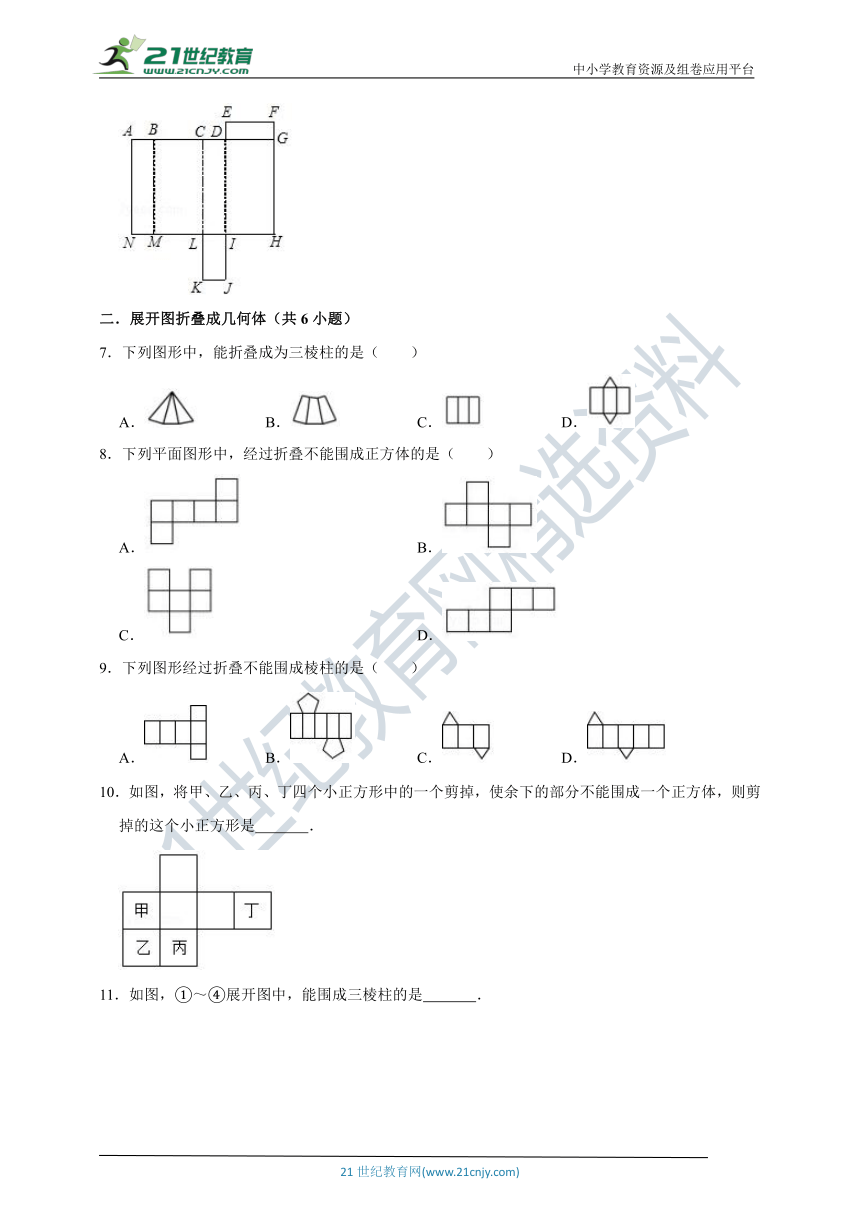
1.下列图形是四棱柱的侧面展开图的是( )
A.
B.
C.
D.
2.如图所示,正方体的展开图为( )
A.
B.
C.
D.
3.下列不是三棱柱展开图的是( )
A.
B.
C.
D.
4.一个圆柱的侧面展开后是一个边长为12.56cm的正方形,这个圆柱的底面半径是
.
5.如图为正方体的一种平面展开图,各面都标有数字,则数字为﹣2的面与其对面上的数字之积是
.
6.如图所示是长方体的平面展开图,设AB=x,若AD=4x,AN=3x.
(1)求长方形DEFG的周长与长方形ABMN的周长(用字母x进行表示);
(2)若长方形DEFG的周长比长方形ABMN的周长少8,求原长方体的体积.
二.展开图折叠成几何体(共6小题)
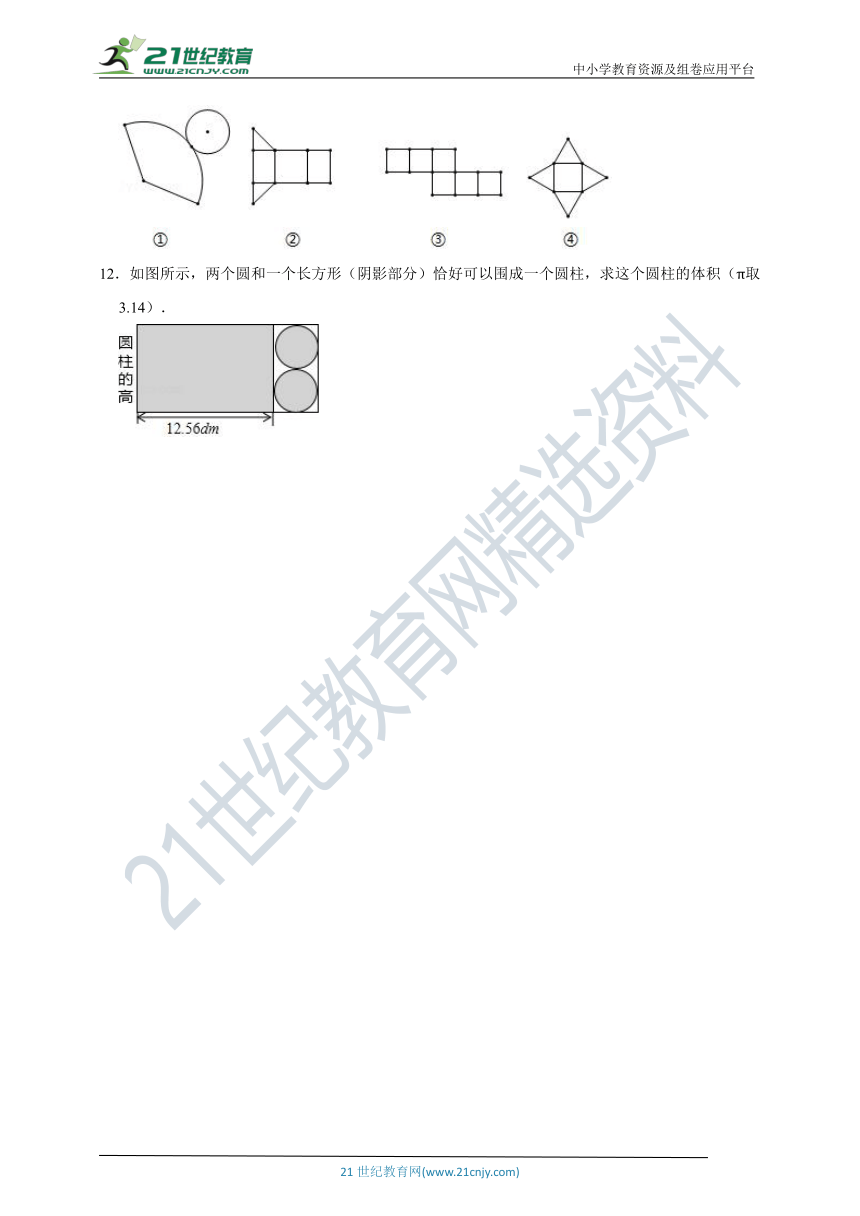
7.下列图形中,能折叠成为三棱柱的是( )
A.
B.
C.
D.
8.下列平面图形中,经过折叠不能围成正方体的是( )
A.
B.
C.
D.
9.下列图形经过折叠不能围成棱柱的是( )
A.
B.
C.
D.
10.如图,将甲、乙、丙、丁四个小正方形中的一个剪掉,使余下的部分不能围成一个正方体,则剪掉的这个小正方形是
.
11.如图,①~④展开图中,能围成三棱柱的是
.
12.如图所示,两个圆和一个长方形(阴影部分)恰好可以围成一个圆柱,求这个圆柱的体积(π取3.14).
4.4
课题学习
设计制作长方体形
参考答案与试题解析
一.几何体的展开图(共6小题)
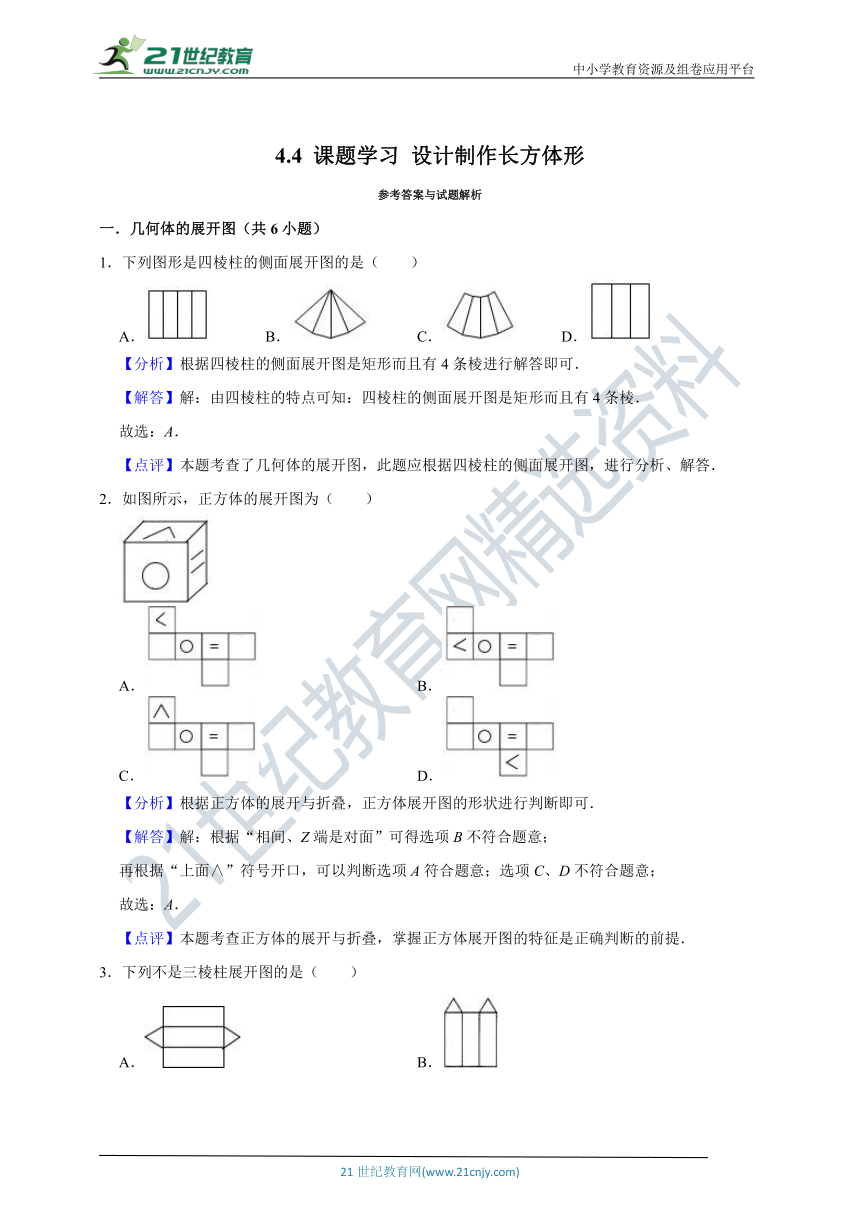
1.下列图形是四棱柱的侧面展开图的是( )
A.
B.
C.
D.
【分析】根据四棱柱的侧面展开图是矩形而且有4条棱进行解答即可.
【解答】解:由四棱柱的特点可知:四棱柱的侧面展开图是矩形而且有4条棱.
故选:A.
【点评】本题考查了几何体的展开图,此题应根据四棱柱的侧面展开图,进行分析、解答.
2.如图所示,正方体的展开图为( )
A.
B.
C.
D.
【分析】根据正方体的展开与折叠,正方体展开图的形状进行判断即可.
【解答】解:根据“相间、Z端是对面”可得选项B不符合题意;
再根据“上面∧”符号开口,可以判断选项A符合题意;选项C、D不符合题意;
故选:A.
【点评】本题考查正方体的展开与折叠,掌握正方体展开图的特征是正确判断的前提.
3.下列不是三棱柱展开图的是( )
A.
B.
C.
D.
【分析】根据三棱柱的两底展开是三角形,侧面展开是三个四边形,可得答案.
【解答】解:A、C、D中间三个长方形能围成三棱柱的侧面,上、下两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.
B围成三棱柱时,两个三角形重合为同一底面,而另一底面没有.故B不能围成三棱柱.
故选:B.
【点评】本题考查了几何体的展开图,注意两底面是对面,展开是两个全等的三角形,侧面展开是三个矩形.
4.一个圆柱的侧面展开后是一个边长为12.56cm的正方形,这个圆柱的底面半径是 2cm .
【分析】由圆柱侧面展开图的特点可知:圆柱的侧面展开后,得到的长方形的长就等于底面周长,高就等于长方形的宽,再据题意可知,这个圆柱的底面周长和高是相等的,现在正方形的边长已知,也就等于底面周长和高已知,再根据圆的周长公式:c=2πr,即可求出底面半径.
【解答】解:12.56÷3.14÷2=2(cm),
答:这个圆柱的底面半径是2cm.
故答案为:2cm.
【点评】本题考查了圆柱的侧面展开图.解答此题的关键是明白:圆柱的侧面展开后是正方形,说明圆柱的底面周长和高相等,根据圆的周长公式解答.
5.如图为正方体的一种平面展开图,各面都标有数字,则数字为﹣2的面与其对面上的数字之积是 ﹣12 .
【分析】根据正方体的平面展开图的特征知,其相对面的两个正方形之间一定相隔一个正方形,所以数字为﹣2的面的对面上的数字是6,其积为﹣12.
【解答】解:数字为﹣2的面的对面上的数字是6,其积为﹣2×6=﹣12.
故答案为:﹣12.
【点评】此题主要考查了正方体相对两个面上的文字,解题的关键是掌握正方体展开图的特点.
6.如图所示是长方体的平面展开图,设AB=x,若AD=4x,AN=3x.
(1)求长方形DEFG的周长与长方形ABMN的周长(用字母x进行表示);
(2)若长方形DEFG的周长比长方形ABMN的周长少8,求原长方体的体积.
【分析】(1)根据AB=x,若AD=4x,AN=3x,即可得到长方形DEFG的周长与长方形ABMN的周长;
(2)根据长方形DEFG的周长比长方形ABMN的周长少8,得到方程,即可得到x的值;根据原长方体的容积为x?2x?3x=6x3,代入x的值即可得到原长方体的体积.
【解答】解:(1)∵AB=x,若AD=4x,AN=3x,
∴长方形DEFG的周长为2(x+2x)=6x,
长方形ABMN的周长为2(x+3x)=8x;
(2)依题意得8x﹣6x=8,
解得:x=4,
原长方体的容积为x?2x?3x=6x3,
将x=4代入,可得体积6x3=384.
故原长方体的体积是384.
【点评】本题主要考查了几何体的展开图,从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
二.展开图折叠成几何体(共6小题)
7.下列图形中,能折叠成为三棱柱的是( )
A.
B.
C.
D.
【分析】根据三棱柱及其表面展开图的特点对各选项分析判断即可得解.
【解答】解:A、折叠后能围成三棱锥,故本选项错误;
B、折叠后能围成缺少上下底面的三棱台,故本选项错误;
C、折叠后能围成缺少上下底面的三棱柱,故本选项错误;
D、折叠后能围成三棱柱,故本选项正确.
故选:D.
【点评】本题考查了三棱柱表面展开图,上、下两底面应在侧面展开图长方形的两侧,且是全等的三角形,不能有两个侧面在两三角形的同一侧.
8.下列平面图形中,经过折叠不能围成正方体的是( )
A.
B.
C.
D.
【分析】根据正方体展开图的常见形式作答即可.
【解答】解:由展开图可知:A、B、D能围成正方体,故不符合题意;
C、围成几何体时,有两个面重合,不能围成正方体,故符合题意.
故选:C.
【点评】本题主要考查展开图折叠成几何体的知识点,注意只要有“田、凹”字格的展开图都不是正方体的表面展开图.
9.下列图形经过折叠不能围成棱柱的是( )
A.
B.
C.
D.
【分析】由平面图形的折叠及棱柱的展开图解题.
【解答】解:A可以围成四棱柱,B可以围成五棱柱,C可以围成三棱柱,D选项侧面上多出2个长方形,故不能围成一个三棱柱.
故选:D.
【点评】本题考查了立体图形的展开与折叠.熟记常见立体图形的表面展开图的特征是解决此类问题的关键.
10.如图,将甲、乙、丙、丁四个小正方形中的一个剪掉,使余下的部分不能围成一个正方体,则剪掉的这个小正方形是 丁 .
【分析】根据正方体的展开图中每个面都有唯一的一个对面进行判断,可得答案.
【解答】解:将如图所示的图形剪去一个小正方形,使余下的部分不能围成一个正方体,编号为甲乙丙丁的小正方形中剪去的是丁,
故答案为:丁.
【点评】本题考查了展开图折叠成几何体,利用正方体的展开图中每个面都有唯一的一个对面是解题的关键.
11.如图,①~④展开图中,能围成三棱柱的是 ② .
【分析】依据展开图的特征,即可得到围成的几何体的类型.
【解答】解:图①能围成圆锥;图②能围成三棱柱;图③能围成正方体;图④能围成四棱锥;
故答案为:②.
【点评】本题主要考查了展开图折成几何体,通过结合立体图形与平面图形的相互转化,去理解和掌握几何体的展开图,要注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.
12.如图所示,两个圆和一个长方形(阴影部分)恰好可以围成一个圆柱,求这个圆柱的体积(π取3.14).
【分析】利用圆柱的体积计算公式进行计算,即可得到这个圆柱的体积.
【解答】解:由图可知,圆柱的半径r=12.56÷(2π)=2(dm),高h=4r=8dm,
则体积V=πr2h=3.14×22×8=100.48(dm3).
答:这个圆柱的体积是100.48dm3.
【点评】本题主要考查考查的是展开图折叠成几何体,求得圆柱的底面半径和高是解题的关键.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/13
9:37:24;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
4.4
课题学习
设计制作长方体形
一.几何体的展开图(共6小题)
1.下列图形是四棱柱的侧面展开图的是( )
A.
B.
C.
D.
2.如图所示,正方体的展开图为( )
A.
B.
C.
D.
3.下列不是三棱柱展开图的是( )
A.
B.
C.
D.
4.一个圆柱的侧面展开后是一个边长为12.56cm的正方形,这个圆柱的底面半径是
.
5.如图为正方体的一种平面展开图,各面都标有数字,则数字为﹣2的面与其对面上的数字之积是
.
6.如图所示是长方体的平面展开图,设AB=x,若AD=4x,AN=3x.
(1)求长方形DEFG的周长与长方形ABMN的周长(用字母x进行表示);
(2)若长方形DEFG的周长比长方形ABMN的周长少8,求原长方体的体积.
二.展开图折叠成几何体(共6小题)
7.下列图形中,能折叠成为三棱柱的是( )
A.
B.
C.
D.
8.下列平面图形中,经过折叠不能围成正方体的是( )
A.
B.
C.
D.
9.下列图形经过折叠不能围成棱柱的是( )
A.
B.
C.
D.
10.如图,将甲、乙、丙、丁四个小正方形中的一个剪掉,使余下的部分不能围成一个正方体,则剪掉的这个小正方形是
.
11.如图,①~④展开图中,能围成三棱柱的是
.
12.如图所示,两个圆和一个长方形(阴影部分)恰好可以围成一个圆柱,求这个圆柱的体积(π取3.14).
4.4
课题学习
设计制作长方体形
参考答案与试题解析
一.几何体的展开图(共6小题)
1.下列图形是四棱柱的侧面展开图的是( )
A.
B.
C.
D.
【分析】根据四棱柱的侧面展开图是矩形而且有4条棱进行解答即可.
【解答】解:由四棱柱的特点可知:四棱柱的侧面展开图是矩形而且有4条棱.
故选:A.
【点评】本题考查了几何体的展开图,此题应根据四棱柱的侧面展开图,进行分析、解答.
2.如图所示,正方体的展开图为( )
A.
B.
C.
D.
【分析】根据正方体的展开与折叠,正方体展开图的形状进行判断即可.
【解答】解:根据“相间、Z端是对面”可得选项B不符合题意;
再根据“上面∧”符号开口,可以判断选项A符合题意;选项C、D不符合题意;
故选:A.
【点评】本题考查正方体的展开与折叠,掌握正方体展开图的特征是正确判断的前提.
3.下列不是三棱柱展开图的是( )
A.
B.
C.
D.
【分析】根据三棱柱的两底展开是三角形,侧面展开是三个四边形,可得答案.
【解答】解:A、C、D中间三个长方形能围成三棱柱的侧面,上、下两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.
B围成三棱柱时,两个三角形重合为同一底面,而另一底面没有.故B不能围成三棱柱.
故选:B.
【点评】本题考查了几何体的展开图,注意两底面是对面,展开是两个全等的三角形,侧面展开是三个矩形.
4.一个圆柱的侧面展开后是一个边长为12.56cm的正方形,这个圆柱的底面半径是 2cm .
【分析】由圆柱侧面展开图的特点可知:圆柱的侧面展开后,得到的长方形的长就等于底面周长,高就等于长方形的宽,再据题意可知,这个圆柱的底面周长和高是相等的,现在正方形的边长已知,也就等于底面周长和高已知,再根据圆的周长公式:c=2πr,即可求出底面半径.
【解答】解:12.56÷3.14÷2=2(cm),
答:这个圆柱的底面半径是2cm.
故答案为:2cm.
【点评】本题考查了圆柱的侧面展开图.解答此题的关键是明白:圆柱的侧面展开后是正方形,说明圆柱的底面周长和高相等,根据圆的周长公式解答.
5.如图为正方体的一种平面展开图,各面都标有数字,则数字为﹣2的面与其对面上的数字之积是 ﹣12 .
【分析】根据正方体的平面展开图的特征知,其相对面的两个正方形之间一定相隔一个正方形,所以数字为﹣2的面的对面上的数字是6,其积为﹣12.
【解答】解:数字为﹣2的面的对面上的数字是6,其积为﹣2×6=﹣12.
故答案为:﹣12.
【点评】此题主要考查了正方体相对两个面上的文字,解题的关键是掌握正方体展开图的特点.
6.如图所示是长方体的平面展开图,设AB=x,若AD=4x,AN=3x.
(1)求长方形DEFG的周长与长方形ABMN的周长(用字母x进行表示);
(2)若长方形DEFG的周长比长方形ABMN的周长少8,求原长方体的体积.
【分析】(1)根据AB=x,若AD=4x,AN=3x,即可得到长方形DEFG的周长与长方形ABMN的周长;
(2)根据长方形DEFG的周长比长方形ABMN的周长少8,得到方程,即可得到x的值;根据原长方体的容积为x?2x?3x=6x3,代入x的值即可得到原长方体的体积.
【解答】解:(1)∵AB=x,若AD=4x,AN=3x,
∴长方形DEFG的周长为2(x+2x)=6x,
长方形ABMN的周长为2(x+3x)=8x;
(2)依题意得8x﹣6x=8,
解得:x=4,
原长方体的容积为x?2x?3x=6x3,
将x=4代入,可得体积6x3=384.
故原长方体的体积是384.
【点评】本题主要考查了几何体的展开图,从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
二.展开图折叠成几何体(共6小题)
7.下列图形中,能折叠成为三棱柱的是( )
A.
B.
C.
D.
【分析】根据三棱柱及其表面展开图的特点对各选项分析判断即可得解.
【解答】解:A、折叠后能围成三棱锥,故本选项错误;
B、折叠后能围成缺少上下底面的三棱台,故本选项错误;
C、折叠后能围成缺少上下底面的三棱柱,故本选项错误;
D、折叠后能围成三棱柱,故本选项正确.
故选:D.
【点评】本题考查了三棱柱表面展开图,上、下两底面应在侧面展开图长方形的两侧,且是全等的三角形,不能有两个侧面在两三角形的同一侧.
8.下列平面图形中,经过折叠不能围成正方体的是( )
A.
B.
C.
D.
【分析】根据正方体展开图的常见形式作答即可.
【解答】解:由展开图可知:A、B、D能围成正方体,故不符合题意;
C、围成几何体时,有两个面重合,不能围成正方体,故符合题意.
故选:C.
【点评】本题主要考查展开图折叠成几何体的知识点,注意只要有“田、凹”字格的展开图都不是正方体的表面展开图.
9.下列图形经过折叠不能围成棱柱的是( )
A.
B.
C.
D.
【分析】由平面图形的折叠及棱柱的展开图解题.
【解答】解:A可以围成四棱柱,B可以围成五棱柱,C可以围成三棱柱,D选项侧面上多出2个长方形,故不能围成一个三棱柱.
故选:D.
【点评】本题考查了立体图形的展开与折叠.熟记常见立体图形的表面展开图的特征是解决此类问题的关键.
10.如图,将甲、乙、丙、丁四个小正方形中的一个剪掉,使余下的部分不能围成一个正方体,则剪掉的这个小正方形是 丁 .
【分析】根据正方体的展开图中每个面都有唯一的一个对面进行判断,可得答案.
【解答】解:将如图所示的图形剪去一个小正方形,使余下的部分不能围成一个正方体,编号为甲乙丙丁的小正方形中剪去的是丁,
故答案为:丁.
【点评】本题考查了展开图折叠成几何体,利用正方体的展开图中每个面都有唯一的一个对面是解题的关键.
11.如图,①~④展开图中,能围成三棱柱的是 ② .
【分析】依据展开图的特征,即可得到围成的几何体的类型.
【解答】解:图①能围成圆锥;图②能围成三棱柱;图③能围成正方体;图④能围成四棱锥;
故答案为:②.
【点评】本题主要考查了展开图折成几何体,通过结合立体图形与平面图形的相互转化,去理解和掌握几何体的展开图,要注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.
12.如图所示,两个圆和一个长方形(阴影部分)恰好可以围成一个圆柱,求这个圆柱的体积(π取3.14).
【分析】利用圆柱的体积计算公式进行计算,即可得到这个圆柱的体积.
【解答】解:由图可知,圆柱的半径r=12.56÷(2π)=2(dm),高h=4r=8dm,
则体积V=πr2h=3.14×22×8=100.48(dm3).
答:这个圆柱的体积是100.48dm3.
【点评】本题主要考查考查的是展开图折叠成几何体,求得圆柱的底面半径和高是解题的关键.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/9/13
9:37:24;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
