4.2.2 由视图到立体图形 同步课件(共26张PPT)
文档属性
| 名称 | 4.2.2 由视图到立体图形 同步课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-11 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
华师大版 初中数学
4.2 立体图形的视图
2.由视图到立体图形
学习目标
1.进一步识别物体从三个方向看到的形状图;(重点)
2.能根据三种视图描述基本几何体或实物原形.(难点)
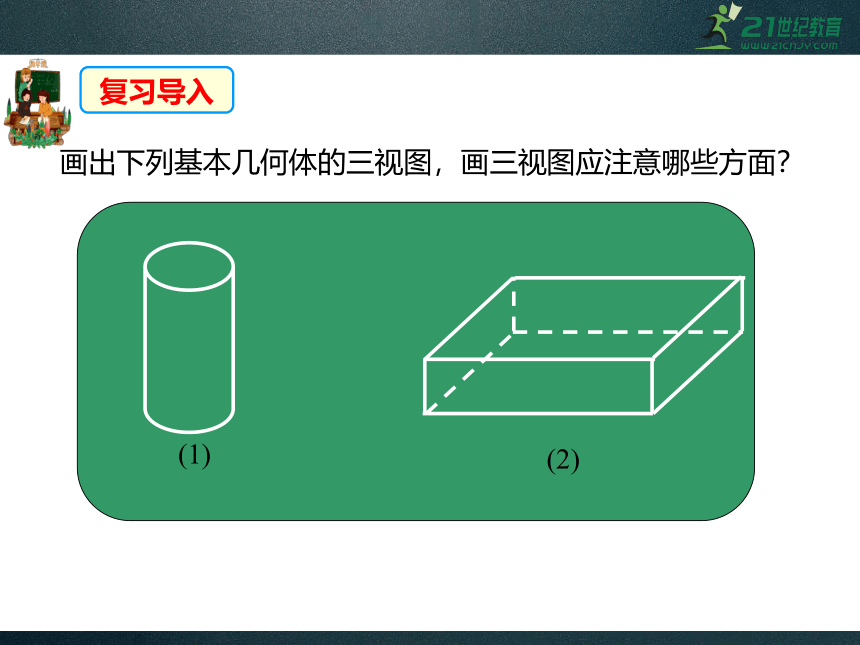
画出下列基本几何体的三视图,画三视图应注意哪些方面?
(1)
(2)
复习导入
由三视图想象立体图形时,要先分别根据主
视图、俯视图、左视图想象立体图形的前面、上
面和左侧面,然后再综合起来考虑整体图形.
一.由视图到立体图形
例3 根据三视图说出立体图形的名称.
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
解:(1) 从三个方向看立体图形,图象都是矩形,可以想象出:整体是长方体,如图所示.
主视图
俯视图
左视图
(1)
例题精析
解:(2)从正面、侧面看立体图形,图象都是等腰三角形;从上面看,图象是圆;可以想象出:整体是圆锥,如图所示.
(2)
主视图
俯视图
左视图
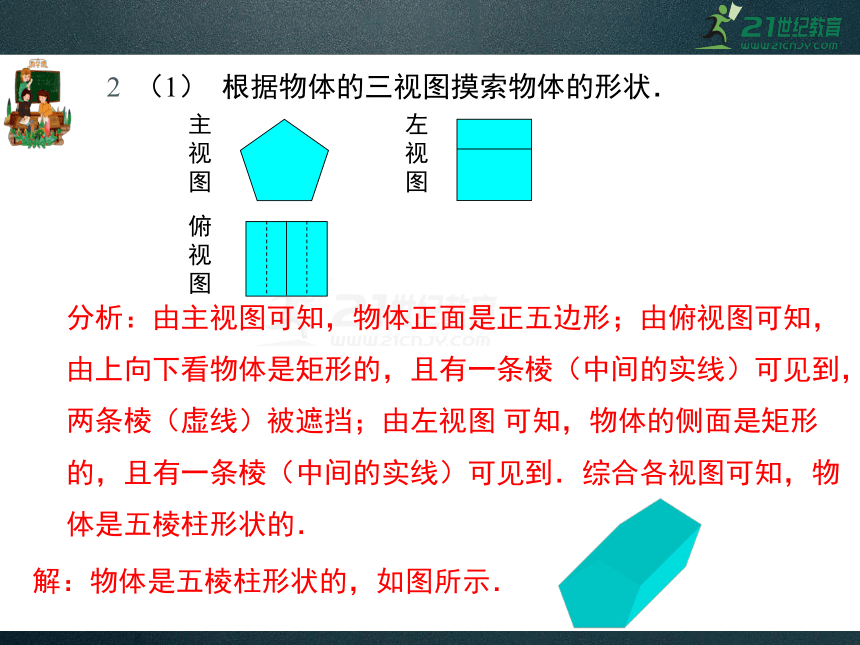
2 (1) 根据物体的三视图摸索物体的形状.
分析:由主视图可知,物体正面是正五边形;由俯视图可知,由上向下看物体是矩形的,且有一条棱(中间的实线)可见到,两条棱(虚线)被遮挡;由左视图 可知,物体的侧面是矩形的,且有一条棱(中间的实线)可见到.综合各视图可知,物体是五棱柱形状的.
解:物体是五棱柱形状的,如图所示.
主视图
俯视图
左视图
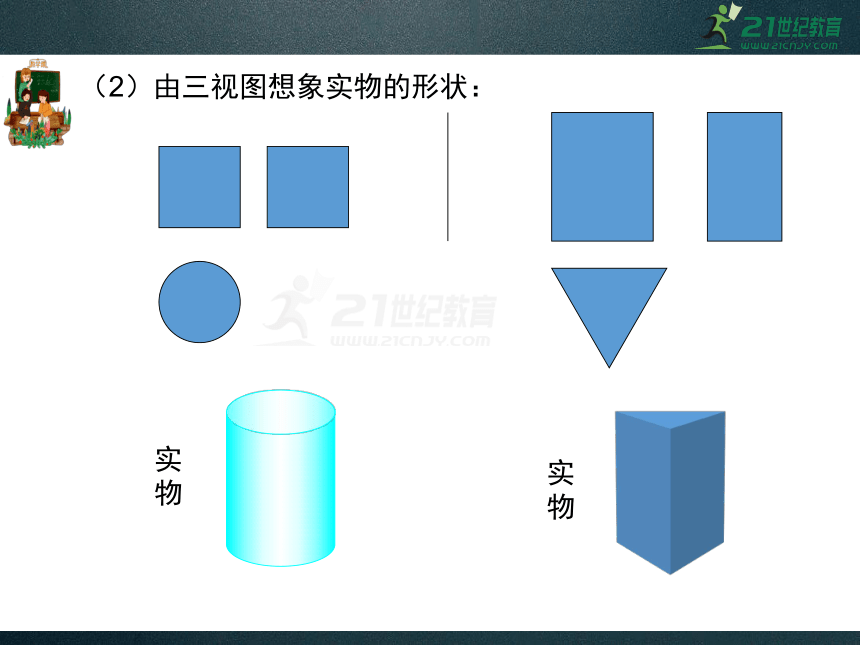
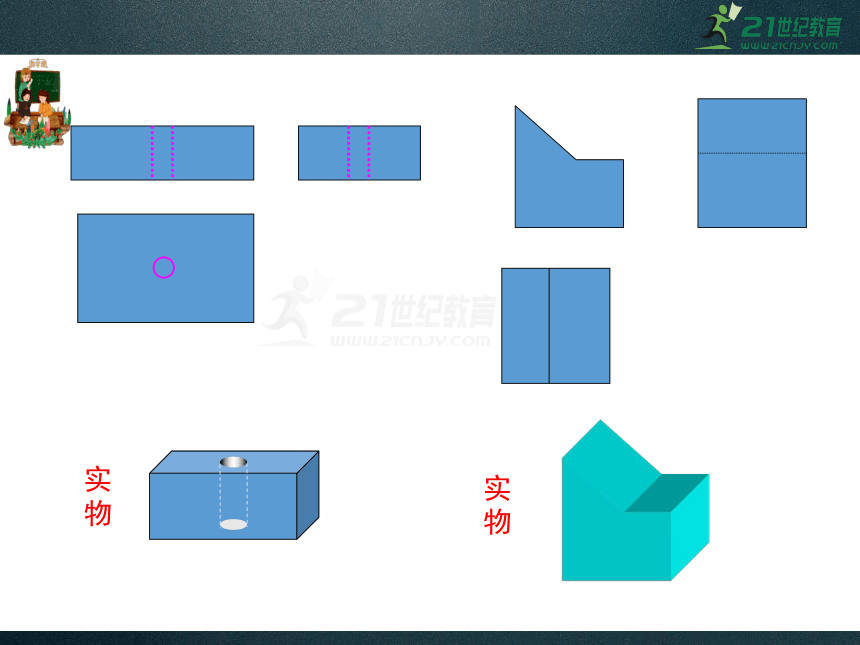
(2)由三视图想象实物的形状:
实物
实物
实物
实物
(3)根据三视图描述物体的形状.
主视图
俯视图
左视图
实物形状
二.由视图到几何体的计算
1. 如图是一个几何体的三视图,
则这个几何体的侧面积是( )
A.18 cm2 B.20 cm2
C.24 cm2 D.6 cm2
A
导引:根据该立体图形的三视图得,该几何体是三
棱柱,且底面是正三角形,该正三角形的边
长为2 cm,该立体图形的侧棱长是3 cm,故
该立体图形的侧面积是(3×2)×3=6×3=
18(cm2).故选A.
2.如图是一个几何体的三视图.
(1)说出这个几何体的名称;
(2)若主视图的宽为4 cm,长
为7 cm,左视图的宽为
3 cm,俯视图中斜边长为
5 cm,求这个几何体中所有棱长的和,
以及它的表面积和体积.
解:(1)三棱柱.
(2)4×2+3×2+5×2+7×3=45(cm),
4×3÷2×2+(3+4+5)×7=96(cm2),
4×3÷2×7=42(cm3).
答:所有棱长的和为45 cm,表面积为
96 cm2,体积为42 cm3.
1 一个几何体的三视图如图所示,则
这个几何体是( )
A.圆柱
B.圆锥
C.长方体
D.正方体
课堂练习
2 一个几何体的三视图如图所示,那
么这个几何体是( )
A.圆锥
B.圆柱
C.长方体
D.三棱柱
3 由若干个棱长为1 cm的正方体堆积成一个几何体,它的三视图如图,则这个几何体的表面积是( )
A.15 cm2
B.18 cm2
C.21 cm2
D.24 cm2
4.某几何体由一些大小相同的小正方
体组成,如图分别是它的主视图和俯视图,那
么要组成该几何体,至少需要多少个这样的小
正方体( )
A.3
B.4
C.5
D.6
5.下面所给的三视图表示什么几何体
直四棱柱
6.下面所给的三视图表示什么几何体
7.下面所给的三视图表示什么几何体
8.用小立方块搭出符合下列三视图的几何体:
主视图
左视图
俯视图
主视图
左视图
俯视图
9.下列是一个物体的三视图,请描述出它的形状.
由三视图描述几何体(或实物原型),一般步骤为:
① 想象:根据各视图想象从各个方向看到的几何体形状;
② 定形:综合确定几何体(或实物原型)的形状;
③ 定大小位置:根据三个视图“长对正,高平齐,宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
课堂小结
作业布置
(1)教材第129页习题4.2第3、4题.
https://www.21cnjy.com/help/help_extract.php
华师大版 初中数学
4.2 立体图形的视图
2.由视图到立体图形
学习目标
1.进一步识别物体从三个方向看到的形状图;(重点)
2.能根据三种视图描述基本几何体或实物原形.(难点)
画出下列基本几何体的三视图,画三视图应注意哪些方面?
(1)
(2)
复习导入
由三视图想象立体图形时,要先分别根据主
视图、俯视图、左视图想象立体图形的前面、上
面和左侧面,然后再综合起来考虑整体图形.
一.由视图到立体图形
例3 根据三视图说出立体图形的名称.
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
解:(1) 从三个方向看立体图形,图象都是矩形,可以想象出:整体是长方体,如图所示.
主视图
俯视图
左视图
(1)
例题精析
解:(2)从正面、侧面看立体图形,图象都是等腰三角形;从上面看,图象是圆;可以想象出:整体是圆锥,如图所示.
(2)
主视图
俯视图
左视图
2 (1) 根据物体的三视图摸索物体的形状.
分析:由主视图可知,物体正面是正五边形;由俯视图可知,由上向下看物体是矩形的,且有一条棱(中间的实线)可见到,两条棱(虚线)被遮挡;由左视图 可知,物体的侧面是矩形的,且有一条棱(中间的实线)可见到.综合各视图可知,物体是五棱柱形状的.
解:物体是五棱柱形状的,如图所示.
主视图
俯视图
左视图
(2)由三视图想象实物的形状:
实物
实物
实物
实物
(3)根据三视图描述物体的形状.
主视图
俯视图
左视图
实物形状
二.由视图到几何体的计算
1. 如图是一个几何体的三视图,
则这个几何体的侧面积是( )
A.18 cm2 B.20 cm2
C.24 cm2 D.6 cm2
A
导引:根据该立体图形的三视图得,该几何体是三
棱柱,且底面是正三角形,该正三角形的边
长为2 cm,该立体图形的侧棱长是3 cm,故
该立体图形的侧面积是(3×2)×3=6×3=
18(cm2).故选A.
2.如图是一个几何体的三视图.
(1)说出这个几何体的名称;
(2)若主视图的宽为4 cm,长
为7 cm,左视图的宽为
3 cm,俯视图中斜边长为
5 cm,求这个几何体中所有棱长的和,
以及它的表面积和体积.
解:(1)三棱柱.
(2)4×2+3×2+5×2+7×3=45(cm),
4×3÷2×2+(3+4+5)×7=96(cm2),
4×3÷2×7=42(cm3).
答:所有棱长的和为45 cm,表面积为
96 cm2,体积为42 cm3.
1 一个几何体的三视图如图所示,则
这个几何体是( )
A.圆柱
B.圆锥
C.长方体
D.正方体
课堂练习
2 一个几何体的三视图如图所示,那
么这个几何体是( )
A.圆锥
B.圆柱
C.长方体
D.三棱柱
3 由若干个棱长为1 cm的正方体堆积成一个几何体,它的三视图如图,则这个几何体的表面积是( )
A.15 cm2
B.18 cm2
C.21 cm2
D.24 cm2
4.某几何体由一些大小相同的小正方
体组成,如图分别是它的主视图和俯视图,那
么要组成该几何体,至少需要多少个这样的小
正方体( )
A.3
B.4
C.5
D.6
5.下面所给的三视图表示什么几何体
直四棱柱
6.下面所给的三视图表示什么几何体
7.下面所给的三视图表示什么几何体
8.用小立方块搭出符合下列三视图的几何体:
主视图
左视图
俯视图
主视图
左视图
俯视图
9.下列是一个物体的三视图,请描述出它的形状.
由三视图描述几何体(或实物原型),一般步骤为:
① 想象:根据各视图想象从各个方向看到的几何体形状;
② 定形:综合确定几何体(或实物原型)的形状;
③ 定大小位置:根据三个视图“长对正,高平齐,宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
课堂小结
作业布置
(1)教材第129页习题4.2第3、4题.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
