4.5.1 点和线 同步课件(共31张PPT)
文档属性
| 名称 | 4.5.1 点和线 同步课件(共31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 10.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-11 09:40:02 | ||
图片预览









文档简介
(共31张PPT)
华师大版 初中数学
4.5 最基本的图形——点和线
第1课时 点和线
学习目标
1.在现实情境中理解线段、射线、直线的概念及他们的区
别与联系;(重点)
2.会用不同的方法表示线段、射线、直线;(难点)
3.了解“两点确定一条直线”的几何事实.
点、线段、射线、直线
1.点
(1)点是最基本的图形,点没有大小,在许多图示
上点常用来表示那些大小尺寸可以忽 略的物体.
(2)点的表示方法:用一个大写字母表示,如 下图
所示的点A,点B.
这可以说成:点动成线
问题 笔尖可以看作是一个点,这个点在纸上运动时,形成了什么?
观察与思考
绷紧的琴弦,,向两方无限延伸的笔直的铁轨等,它们可以分别抽象出哪些简单的平面图形呢?
图 形 联 系 区 别
有无
方向 表示
方法 端点
个数 有无
长度
线
段
射
线
直
线
无
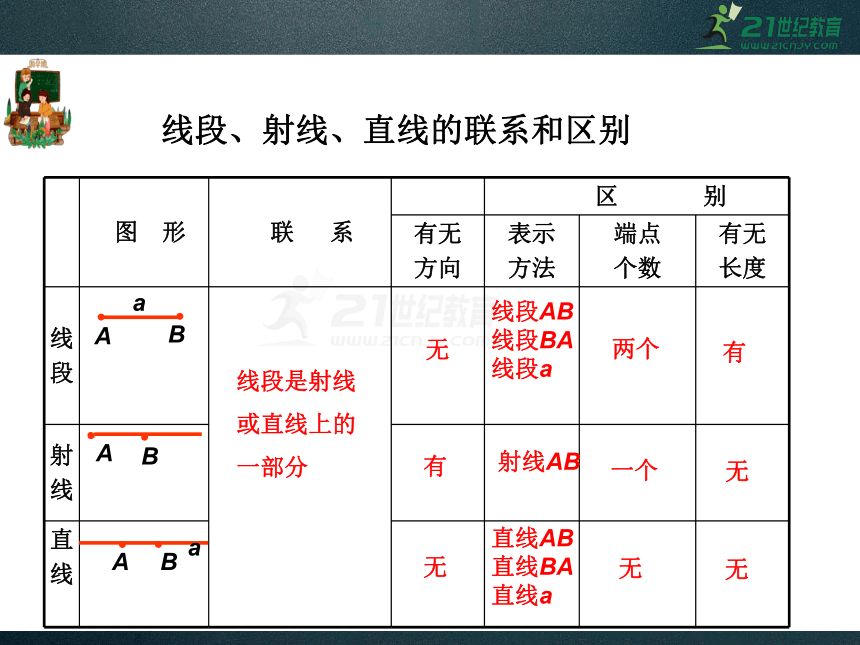
线段、射线、直线的联系和区别
线段AB
线段BA
线段a
两个
有
射线AB
一个
无
直线AB直线BA
直线a
无
A
B
线段是射线或直线上的一部分
A
B
a
B
A
a
无
有
无
例1 如图所示,下列说法正确的是( )
A.直线AB和直线CD是不同的直线
B.射线AB和射线BA是同一条射线
C.线段AB和线段BA是同一条线段
D.直线AD=AB+BC+CD
典例精析
解析:在直线上任意两个大写字母都可以表示这条直线,所以A错;表示射线时,第一个字母表示射线的端点.端点字母不同,射线必然不同,所以B错;直线无长短,所以D错.
C
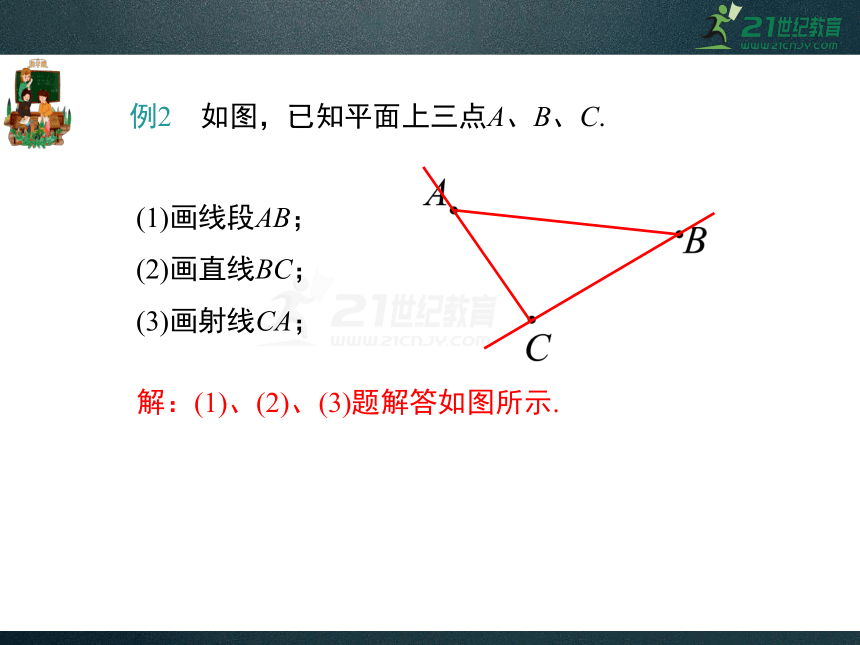
例2 如图,已知平面上三点A、B、C.
(1)画线段AB;
(2)画直线BC;
(3)画射线CA;
解:(1)、(2)、(3)题解答如图所示.
(4)如何由线段AB得到射线AB和直线AB呢?
(4)将线段AB向AB方向延伸得到射线AB,将线段AB向两个方向延伸得到直线AB,如图所示.
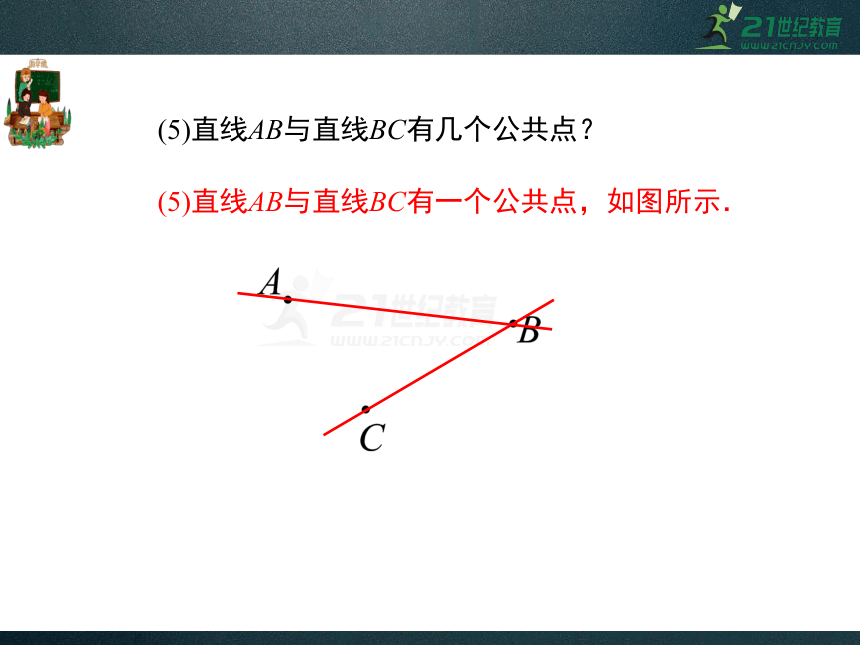
(5)直线AB与直线BC有一个公共点,如图所示.
(5)直线AB与直线BC有几个公共点?
例3 图中共有几条线段?说明你分析这个问题的具体思路.
解:以A为端点的线段有AB,AC,AD,AE,共4条,以B为端点且与前面不重复的线段有BC,BD,BE,共3条,以C为端点且与前面不重复的线段有CD,CE,共2条,以D为端点且与前面不重复的线段有DE,共1条,从而共有4+3+2+1=10(条)线段.
联系:都是直的,线段向一个方向延伸可以得到射线, 线段向两个方向延伸可以得到直线.
区别:直线可以向两个方向无限延伸,射线可以向一个方向延伸,线段本身不能延伸.
总结归纳
线段、射线、直线的联系与区别
由此可知, 射线、线段都是直线的一部分.线段是射线的一部分.
直线没有端点,射线有一个端点,线段有两个端点.
线段、直线的基本事实
试一试
如图,从A地到B地有三条路径,你会选择哪一条?
问题1 从A地到B地有三条路径,你会选择哪一条
线段AB的长度,就是A、B两点间的距离.
两点之间,线段最短.
A
B
C
问题引导
解析:在MN上任选一点P,它到A,B的距离即线段PA与PB的长,结合两点之间线段最短可求.
例4 如图所示,直线MN表示一条铁路,铁路两旁各有一点A和B,表示两个工厂.要在铁路上建一货站,使它到两厂距离之和最短,这个货站应建在何处?
解:连接AB,交MN于点P,则这个货站应建在点P处.
P
P
(1)两点之间的距离的概念描述的是数量,而不是图形,指的是连接两点的线段的长度,而不是线段本身.
(2)在解决选择位置、求最短距离等问题时,通常转化为“两点之间线段最短”.
总结归纳
问题2 过一点 O 可以画几条直线?
问题3 过两点A、B可以画几条直线?
·O
A
B
经过两点有且只有一条直线.
结论:
举一个能反映“经过两点有且只有一条直线”的实例.
练一练
植树时,只要定出两个树坑的位置就能确定同一行的树坑所在的直线.
一、判断题:
1.拉紧的细绳子不是射线而是线段.( )
2.直线AB与直线BA是同一条直线.( )
3.射线AB与射线BA是同一条射线.( )
4.线段AB与线段BA是同一条线段.( )
5.射线比线段长也可能线段比射线长.( )
6.在两个点之间,一定是线段最短.( )
7.线段上只有两个点.( )
8.射线AB和射线AC是同一条射线.( )
﹒
A
B
C
﹒
﹒
√
√
×
×
×
√
√
√
课堂练习
2.经过同一平面内任意三点中的两点共可以
画出( )
A.一条直线 B.两条直线
C.一条或三条直线 D.三条直线
3.下列说法正确的是( )
A.两点之间,直线最短
B.线段MN就是M,N两点间的距离
C.在连接两点的所有线中,最短的连线的长度就
是这两点间的距离
D.从武汉到北京,火车行走的路程就是武汉到北
京的距离
4.把一条弯曲的公路改成直道,可以缩短路程,用几何知识解释其道理正确的是( )
A.两点确定一条直线
B.两点之间,直线最短
C.两点之间,线段最短
D.两点之间,射线最短
6.下列现象:①农民伯伯拉绳插秧;②解放军叔叔打靶瞄准;③学生早操队列对齐;④在墙上至少要用两根钉子才能把木条固定;⑤改直弯曲的河道,缩短航程.其中可以用“两点确定一条直线”来解释的有__________.(填序号)
5.下列说法中,错误的是( )
A.经过一点的直线可以有无数条
B.经过两点的直线只有一条
C.一条直线只能用一个字母表示
D.线段EF与线段FE是同一条线段
C
①②③④
7.指出下图中线段、射线、直线分别有多少条?并把线段表示出来.
解:线段有3条,分别为线段AB、线段AC、线段BC.
射线有6条.
直线有1条.
自己尝试把6条射线画出来
A
B
C
8.巩固练习
(1)找出图中的线段、射线、直线,并把它们表示出来.
(2)将图中各顶点标上字母,写出所有的线段.
面
棱
顶点
9. 如图,从小明家到学校共有三条路,小明为了尽快到学校,应选择第_________条路,用数学知识解释为___________________.
小明家
学校
(1)
(2)
(3)
(2)
两点之间,线段最短
10.请同学们画直线.
(1)过点A画直线,能画多少条?
(2)过两点A、B能画几条直线?
(3)在墙上钉木条,要使其牢固,应钉几颗钉子?这是为什么?
(4)站队时,怎样才能站成一条直线?
经过两点有一条直线,并且只有一条直线.
四、课堂小结
线段、射线、直线的联系与区别
两点确定一条直线
点和线
两点之间,线段最短
教材习题4.5第1、2题.
五、布置作业
https://www.21cnjy.com/help/help_extract.php
华师大版 初中数学
4.5 最基本的图形——点和线
第1课时 点和线
学习目标
1.在现实情境中理解线段、射线、直线的概念及他们的区
别与联系;(重点)
2.会用不同的方法表示线段、射线、直线;(难点)
3.了解“两点确定一条直线”的几何事实.
点、线段、射线、直线
1.点
(1)点是最基本的图形,点没有大小,在许多图示
上点常用来表示那些大小尺寸可以忽 略的物体.
(2)点的表示方法:用一个大写字母表示,如 下图
所示的点A,点B.
这可以说成:点动成线
问题 笔尖可以看作是一个点,这个点在纸上运动时,形成了什么?
观察与思考
绷紧的琴弦,,向两方无限延伸的笔直的铁轨等,它们可以分别抽象出哪些简单的平面图形呢?
图 形 联 系 区 别
有无
方向 表示
方法 端点
个数 有无
长度
线
段
射
线
直
线
无
线段、射线、直线的联系和区别
线段AB
线段BA
线段a
两个
有
射线AB
一个
无
直线AB直线BA
直线a
无
A
B
线段是射线或直线上的一部分
A
B
a
B
A
a
无
有
无
例1 如图所示,下列说法正确的是( )
A.直线AB和直线CD是不同的直线
B.射线AB和射线BA是同一条射线
C.线段AB和线段BA是同一条线段
D.直线AD=AB+BC+CD
典例精析
解析:在直线上任意两个大写字母都可以表示这条直线,所以A错;表示射线时,第一个字母表示射线的端点.端点字母不同,射线必然不同,所以B错;直线无长短,所以D错.
C
例2 如图,已知平面上三点A、B、C.
(1)画线段AB;
(2)画直线BC;
(3)画射线CA;
解:(1)、(2)、(3)题解答如图所示.
(4)如何由线段AB得到射线AB和直线AB呢?
(4)将线段AB向AB方向延伸得到射线AB,将线段AB向两个方向延伸得到直线AB,如图所示.
(5)直线AB与直线BC有一个公共点,如图所示.
(5)直线AB与直线BC有几个公共点?
例3 图中共有几条线段?说明你分析这个问题的具体思路.
解:以A为端点的线段有AB,AC,AD,AE,共4条,以B为端点且与前面不重复的线段有BC,BD,BE,共3条,以C为端点且与前面不重复的线段有CD,CE,共2条,以D为端点且与前面不重复的线段有DE,共1条,从而共有4+3+2+1=10(条)线段.
联系:都是直的,线段向一个方向延伸可以得到射线, 线段向两个方向延伸可以得到直线.
区别:直线可以向两个方向无限延伸,射线可以向一个方向延伸,线段本身不能延伸.
总结归纳
线段、射线、直线的联系与区别
由此可知, 射线、线段都是直线的一部分.线段是射线的一部分.
直线没有端点,射线有一个端点,线段有两个端点.
线段、直线的基本事实
试一试
如图,从A地到B地有三条路径,你会选择哪一条?
问题1 从A地到B地有三条路径,你会选择哪一条
线段AB的长度,就是A、B两点间的距离.
两点之间,线段最短.
A
B
C
问题引导
解析:在MN上任选一点P,它到A,B的距离即线段PA与PB的长,结合两点之间线段最短可求.
例4 如图所示,直线MN表示一条铁路,铁路两旁各有一点A和B,表示两个工厂.要在铁路上建一货站,使它到两厂距离之和最短,这个货站应建在何处?
解:连接AB,交MN于点P,则这个货站应建在点P处.
P
P
(1)两点之间的距离的概念描述的是数量,而不是图形,指的是连接两点的线段的长度,而不是线段本身.
(2)在解决选择位置、求最短距离等问题时,通常转化为“两点之间线段最短”.
总结归纳
问题2 过一点 O 可以画几条直线?
问题3 过两点A、B可以画几条直线?
·O
A
B
经过两点有且只有一条直线.
结论:
举一个能反映“经过两点有且只有一条直线”的实例.
练一练
植树时,只要定出两个树坑的位置就能确定同一行的树坑所在的直线.
一、判断题:
1.拉紧的细绳子不是射线而是线段.( )
2.直线AB与直线BA是同一条直线.( )
3.射线AB与射线BA是同一条射线.( )
4.线段AB与线段BA是同一条线段.( )
5.射线比线段长也可能线段比射线长.( )
6.在两个点之间,一定是线段最短.( )
7.线段上只有两个点.( )
8.射线AB和射线AC是同一条射线.( )
﹒
A
B
C
﹒
﹒
√
√
×
×
×
√
√
√
课堂练习
2.经过同一平面内任意三点中的两点共可以
画出( )
A.一条直线 B.两条直线
C.一条或三条直线 D.三条直线
3.下列说法正确的是( )
A.两点之间,直线最短
B.线段MN就是M,N两点间的距离
C.在连接两点的所有线中,最短的连线的长度就
是这两点间的距离
D.从武汉到北京,火车行走的路程就是武汉到北
京的距离
4.把一条弯曲的公路改成直道,可以缩短路程,用几何知识解释其道理正确的是( )
A.两点确定一条直线
B.两点之间,直线最短
C.两点之间,线段最短
D.两点之间,射线最短
6.下列现象:①农民伯伯拉绳插秧;②解放军叔叔打靶瞄准;③学生早操队列对齐;④在墙上至少要用两根钉子才能把木条固定;⑤改直弯曲的河道,缩短航程.其中可以用“两点确定一条直线”来解释的有__________.(填序号)
5.下列说法中,错误的是( )
A.经过一点的直线可以有无数条
B.经过两点的直线只有一条
C.一条直线只能用一个字母表示
D.线段EF与线段FE是同一条线段
C
①②③④
7.指出下图中线段、射线、直线分别有多少条?并把线段表示出来.
解:线段有3条,分别为线段AB、线段AC、线段BC.
射线有6条.
直线有1条.
自己尝试把6条射线画出来
A
B
C
8.巩固练习
(1)找出图中的线段、射线、直线,并把它们表示出来.
(2)将图中各顶点标上字母,写出所有的线段.
面
棱
顶点
9. 如图,从小明家到学校共有三条路,小明为了尽快到学校,应选择第_________条路,用数学知识解释为___________________.
小明家
学校
(1)
(2)
(3)
(2)
两点之间,线段最短
10.请同学们画直线.
(1)过点A画直线,能画多少条?
(2)过两点A、B能画几条直线?
(3)在墙上钉木条,要使其牢固,应钉几颗钉子?这是为什么?
(4)站队时,怎样才能站成一条直线?
经过两点有一条直线,并且只有一条直线.
四、课堂小结
线段、射线、直线的联系与区别
两点确定一条直线
点和线
两点之间,线段最短
教材习题4.5第1、2题.
五、布置作业
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
