4.5.2 线段的长短比较 同步课件(共24张PPT)
文档属性
| 名称 | 4.5.2 线段的长短比较 同步课件(共24张PPT) |  | |
| 格式 | rar | ||
| 文件大小 | 9.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-11 09:42:27 | ||
图片预览








文档简介
人教版 初中数学
4.5 最基本的图形——点和线
2.线段的长短比较
学习目标
1.理解线段中点的概念及表示方法;(难点)
2.能借助直尺、圆规等工具比较两条线段的长短(重点)
难点)
问题 你和同学是怎样比较个子高矮的?
方法一
方法二
思考 怎样比较两条线段的长短呢?
观察与思考
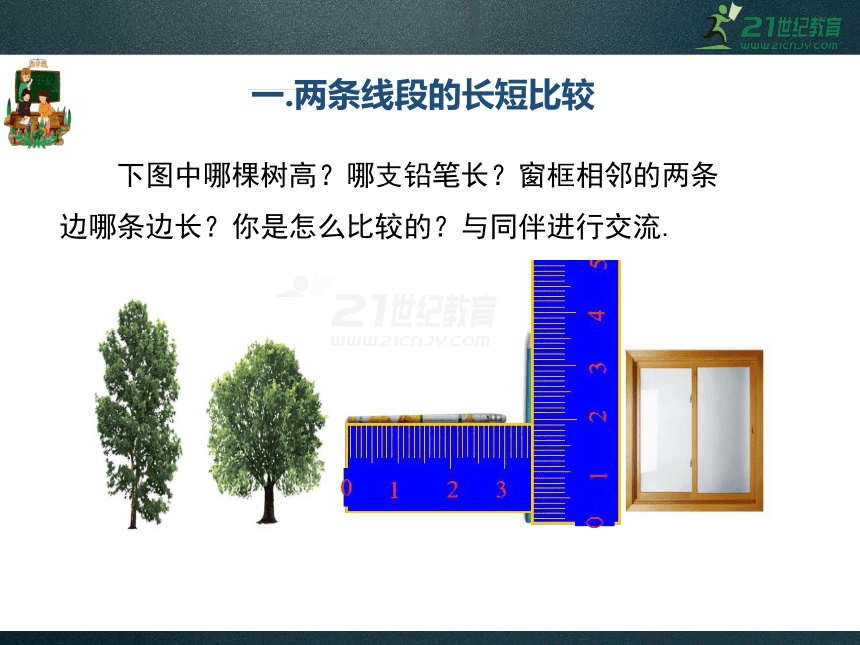
一.两条线段的长短比较
下图中哪棵树高?哪支铅笔长?窗框相邻的两条边哪条边长?你是怎么比较的?与同伴进行交流.
思考:怎样比较两条线段的长短??
(1) 度量法
(2) 叠合法
将其中一条线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上.
用刻度尺量出它们的长度,再进行比较.
A B
C D
a
b
借助尺规作图的方法
C
D
(A)
B
<
叠合法结论:
B
A
C
(B)
(A)
D
A
B
C
D
B
(A)
B
A
1.若点A与点C重合,点B落在C、D之间,那么AB___CD.
2.若点A与点C重合,点B与点D_____,那么AB=CD.
3.若点A与点C重合,点B落在CD的延长线上,那么AB ___ CD.
重合
>
二.线段的中点及长度计算
思考 如何找到一条绳子的中点呢?
可以把绳子对折找中点.
你还有其他方法吗?
点M把线段AB分成相等的两条线段AM和BM,点M叫做线段AB的中点.
因为M是线段AB的中点
所以AM= MB = AB
(或AB=2AM=2MB)
中点定义
数学语言:
总结归纳
A
M
B
例 如图,在直线上有A,B,C三点,AB=4 cm,BC=3 cm,如果O是线段AC的中点,求线段OB的长度.
解:因为AB=4 cm,BC=3 cm,
所以AC=AB+ BC=7 cm.
因为点O是线段AC的中点,
所以OC= AC=3.5 cm.
所以OB=OC-BC=3.5-3=0.5(cm).
A
O
C
B
典例精析
(1)逐段计算:求线段的长度,主要围绕线段的和、差、倍、分关系展开.若每一条线段的长度均已确定,所求问题可迎刃而解.
计算线段长度的一般方法:
(2)整体转化:巧妙转化是解题关键.首先将线段转化为两条线段的和,然后再通过线段的中点的等量关系进行替换,将未知线段转化为已知线段.
总结归纳
已知线段AB=6 cm,点C是AB的中点,那么AC与BC分别等于多少?
BC= AC=3 cm
若条件再添加D是线段CB的中点,那么AD有多长呢?
AD=4.5 cm
根据所示图形填空:
(1) AB+ BC =( );
(2) AD = ( ) +CD;
(3) CD=AD-( );
(4) BD = CD + ( )=AD-( );
(5) AC-AB+CD = ( )=BC + ( ).
1
课堂练习
2.如图,已知点C是线段AD的中点,AC=
1.5cm, ?BC= 2. 2 cm,那么AD= ( )cm, BD =( )cm.
点C在线段AB上,下列条件中不能确定点C是线段AB中点的是( )
A.AC=BC B.AC+BC=AB
C.AB=2AC D.BC= AB
3
4.下列说法正确的是( )
A.若AC= AB,则C是AB的中点
B.若AB=2CB,则C是AB的中点
C.若AC=BC,则C是AB的中点
D.若AC=BC= AB,则C是AB的中点
5.已知线段AB=10 cm,点C是直线AB上一点,BC=4 cm,若M是AC的中点,N是BC的中点,则线段MN的长度是( )
A.7 cm B.3 cm
C.7 cm或3 cm D.5 cm
6.如图,C是线段AB上的一点,M是线段AC的中点,若AB=8 cm,BC=2 cm,则MC的长是( )
A.2 cm B.3 cm
C.4 cm D.6 cm
7.(1)数轴上A、B两点所表示的数是-5和1,那么线段AB的长是 个单位长度,线段AB的中点所表示的数是 .
(2)已知线段AC和BC在同一条直线上,如果AC=5.6 cm,BC=2.4 cm,求线段AC和BC的中点之间的距离.
6
-2
线段AC和BC的中点之间的距离为:4 cm或1.6 cm.
8.如图,由AB=CD可得AC与BD的大小关系正确的是( )
A.AC>BD B.AC<BD
C.AC=BD D.不能确定
9.已知M是线段AB的中点,①AB=2AM;②BM= AB;③AM=BM;④AM+BM=AB.上面四个式子中,正确的有( )
A.1个 B.2个 C.3个 D.4个
10.已知线段AB=6 cm,在直线AB上画线段AC=2 cm,则BC的长是___________.
C
D
4cm或8cm
A
D
C
B
11.如图,AB=6 cm,点C是线段AB的中点,点D是线段CB的中点,求AC,AD的长度.
解:AC=3 cm,AD=4.5 cm.
A
D
C
B
四、小结
小结:请你谈谈本节课的收获.
了解线段中点的概念,并能简单运用它来解决问题.
线段的长短比较
比较线段大小的方法
线段的中点与计算
度量法
叠合法
五、作业
作业:教材第143页练习第1、2、3题,习题4.5第4、5题.
https://www.21cnjy.com/help/help_extract.php
4.5 最基本的图形——点和线
2.线段的长短比较
学习目标
1.理解线段中点的概念及表示方法;(难点)
2.能借助直尺、圆规等工具比较两条线段的长短(重点)
难点)
问题 你和同学是怎样比较个子高矮的?
方法一
方法二
思考 怎样比较两条线段的长短呢?
观察与思考
一.两条线段的长短比较
下图中哪棵树高?哪支铅笔长?窗框相邻的两条边哪条边长?你是怎么比较的?与同伴进行交流.
思考:怎样比较两条线段的长短??
(1) 度量法
(2) 叠合法
将其中一条线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上.
用刻度尺量出它们的长度,再进行比较.
A B
C D
a
b
借助尺规作图的方法
C
D
(A)
B
<
叠合法结论:
B
A
C
(B)
(A)
D
A
B
C
D
B
(A)
B
A
1.若点A与点C重合,点B落在C、D之间,那么AB___CD.
2.若点A与点C重合,点B与点D_____,那么AB=CD.
3.若点A与点C重合,点B落在CD的延长线上,那么AB ___ CD.
重合
>
二.线段的中点及长度计算
思考 如何找到一条绳子的中点呢?
可以把绳子对折找中点.
你还有其他方法吗?
点M把线段AB分成相等的两条线段AM和BM,点M叫做线段AB的中点.
因为M是线段AB的中点
所以AM= MB = AB
(或AB=2AM=2MB)
中点定义
数学语言:
总结归纳
A
M
B
例 如图,在直线上有A,B,C三点,AB=4 cm,BC=3 cm,如果O是线段AC的中点,求线段OB的长度.
解:因为AB=4 cm,BC=3 cm,
所以AC=AB+ BC=7 cm.
因为点O是线段AC的中点,
所以OC= AC=3.5 cm.
所以OB=OC-BC=3.5-3=0.5(cm).
A
O
C
B
典例精析
(1)逐段计算:求线段的长度,主要围绕线段的和、差、倍、分关系展开.若每一条线段的长度均已确定,所求问题可迎刃而解.
计算线段长度的一般方法:
(2)整体转化:巧妙转化是解题关键.首先将线段转化为两条线段的和,然后再通过线段的中点的等量关系进行替换,将未知线段转化为已知线段.
总结归纳
已知线段AB=6 cm,点C是AB的中点,那么AC与BC分别等于多少?
BC= AC=3 cm
若条件再添加D是线段CB的中点,那么AD有多长呢?
AD=4.5 cm
根据所示图形填空:
(1) AB+ BC =( );
(2) AD = ( ) +CD;
(3) CD=AD-( );
(4) BD = CD + ( )=AD-( );
(5) AC-AB+CD = ( )=BC + ( ).
1
课堂练习
2.如图,已知点C是线段AD的中点,AC=
1.5cm, ?BC= 2. 2 cm,那么AD= ( )cm, BD =( )cm.
点C在线段AB上,下列条件中不能确定点C是线段AB中点的是( )
A.AC=BC B.AC+BC=AB
C.AB=2AC D.BC= AB
3
4.下列说法正确的是( )
A.若AC= AB,则C是AB的中点
B.若AB=2CB,则C是AB的中点
C.若AC=BC,则C是AB的中点
D.若AC=BC= AB,则C是AB的中点
5.已知线段AB=10 cm,点C是直线AB上一点,BC=4 cm,若M是AC的中点,N是BC的中点,则线段MN的长度是( )
A.7 cm B.3 cm
C.7 cm或3 cm D.5 cm
6.如图,C是线段AB上的一点,M是线段AC的中点,若AB=8 cm,BC=2 cm,则MC的长是( )
A.2 cm B.3 cm
C.4 cm D.6 cm
7.(1)数轴上A、B两点所表示的数是-5和1,那么线段AB的长是 个单位长度,线段AB的中点所表示的数是 .
(2)已知线段AC和BC在同一条直线上,如果AC=5.6 cm,BC=2.4 cm,求线段AC和BC的中点之间的距离.
6
-2
线段AC和BC的中点之间的距离为:4 cm或1.6 cm.
8.如图,由AB=CD可得AC与BD的大小关系正确的是( )
A.AC>BD B.AC<BD
C.AC=BD D.不能确定
9.已知M是线段AB的中点,①AB=2AM;②BM= AB;③AM=BM;④AM+BM=AB.上面四个式子中,正确的有( )
A.1个 B.2个 C.3个 D.4个
10.已知线段AB=6 cm,在直线AB上画线段AC=2 cm,则BC的长是___________.
C
D
4cm或8cm
A
D
C
B
11.如图,AB=6 cm,点C是线段AB的中点,点D是线段CB的中点,求AC,AD的长度.
解:AC=3 cm,AD=4.5 cm.
A
D
C
B
四、小结
小结:请你谈谈本节课的收获.
了解线段中点的概念,并能简单运用它来解决问题.
线段的长短比较
比较线段大小的方法
线段的中点与计算
度量法
叠合法
五、作业
作业:教材第143页练习第1、2、3题,习题4.5第4、5题.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
