5.2.2 平行线的判定 同步课件(共36张PPT)
文档属性
| 名称 | 5.2.2 平行线的判定 同步课件(共36张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 9.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-11 13:34:24 | ||
图片预览








文档简介
(共36张PPT)
华师大版 初中数学
5.2 平行线
第2课时 平行线的判定
学习目标
1.掌握平行线的三种判定方法,会运用判定方法来判断两条
直线是否平行;(重点)
2.能够根据平行线的判定方法进行简单的推理.
问题1 两条直线的位置关系有哪几种?
问题2 怎样的两条直线平行?
问题3 上节课你学了平行线的哪些内容?
相交(包括垂直)和平行两种.
在同一平面内,不相交的两条直线平行.
如果两条直线都与第三条直线平行,那么这两条直线互相平行.
经过直线外一点,有且只有一条直线与已知直线平行.
回顾与思考
思考
根据平行线的定义,如果平面内的两条直线不相交,就可以判断这两条直线平行.但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据两条直线是否平行,那么有没有其他判定方法呢?
●
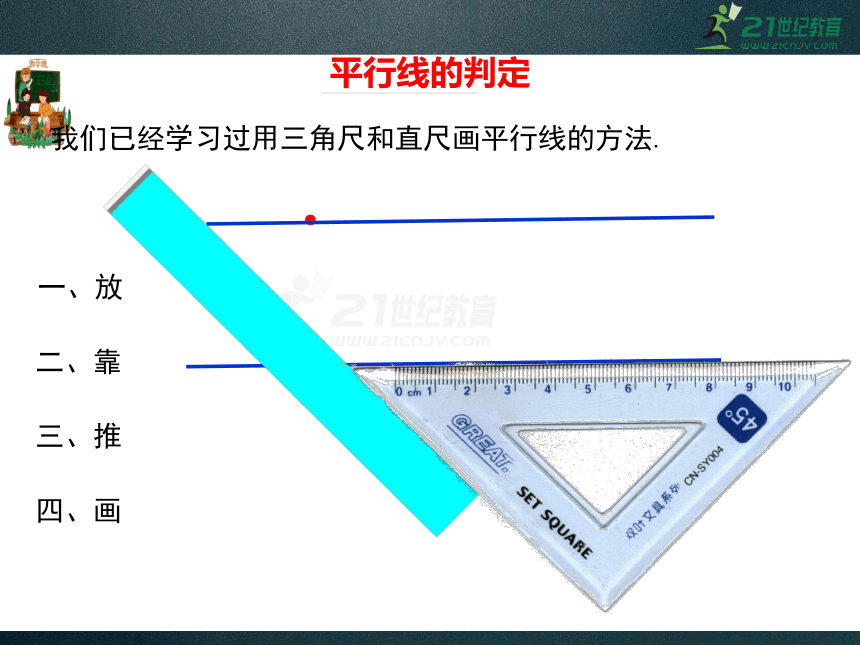
一、放
二、靠
三、推
四、画
我们已经学习过用三角尺和直尺画平行线的方法.
平行线的判定
●
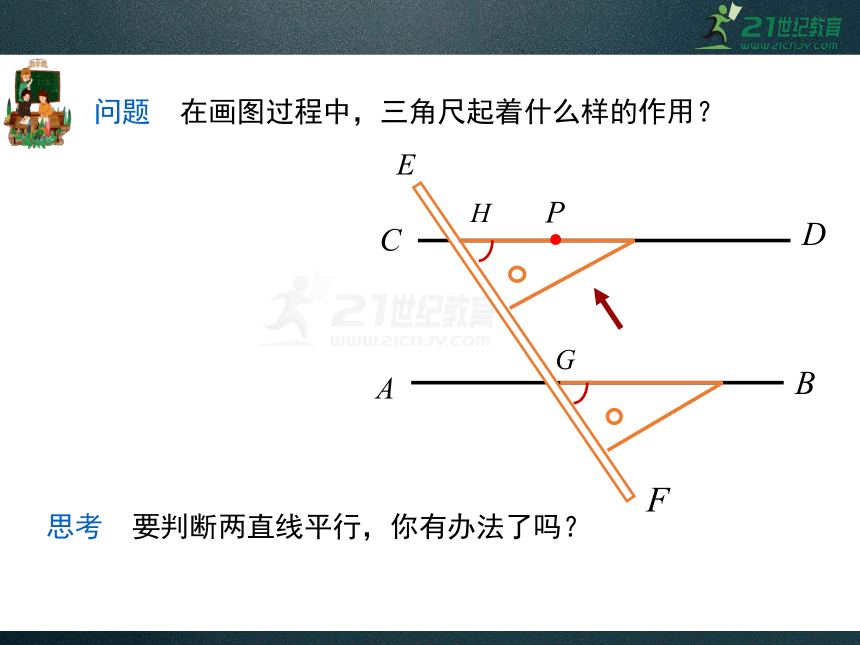
问题 在画图过程中,三角尺起着什么样的作用?
思考 要判断两直线平行,你有办法了吗?
b
A
2
1
a
B
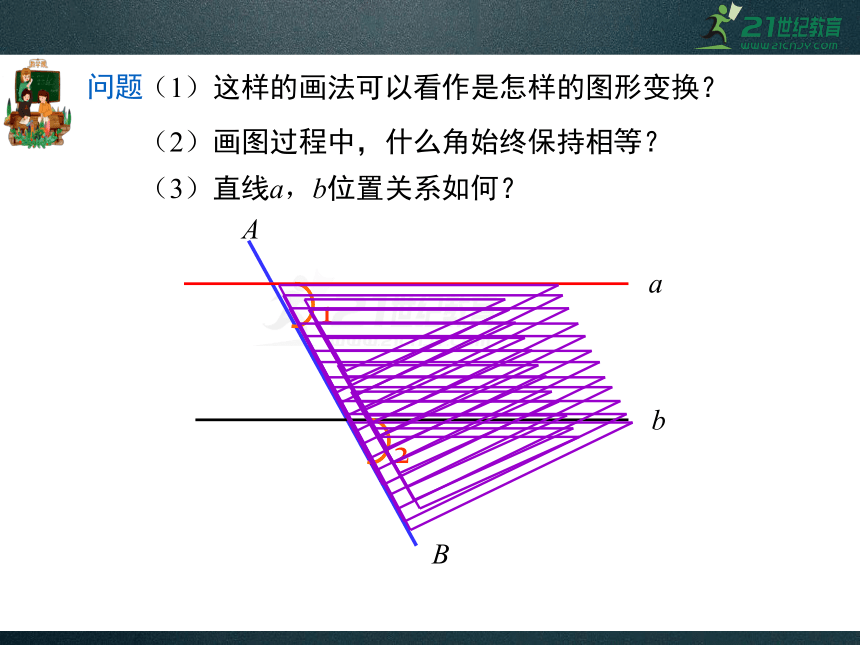
(1)这样的画法可以看作是怎样的图形变换?
(2)画图过程中,什么角始终保持相等?
(3)直线a,b位置关系如何?
问题
(4)请将其最初和最终的特殊位置抽象成几何图形:
1
2
l2
l1
A
B
(5) 由上面的操作过程,你能发现判定两直线平行的方法吗?
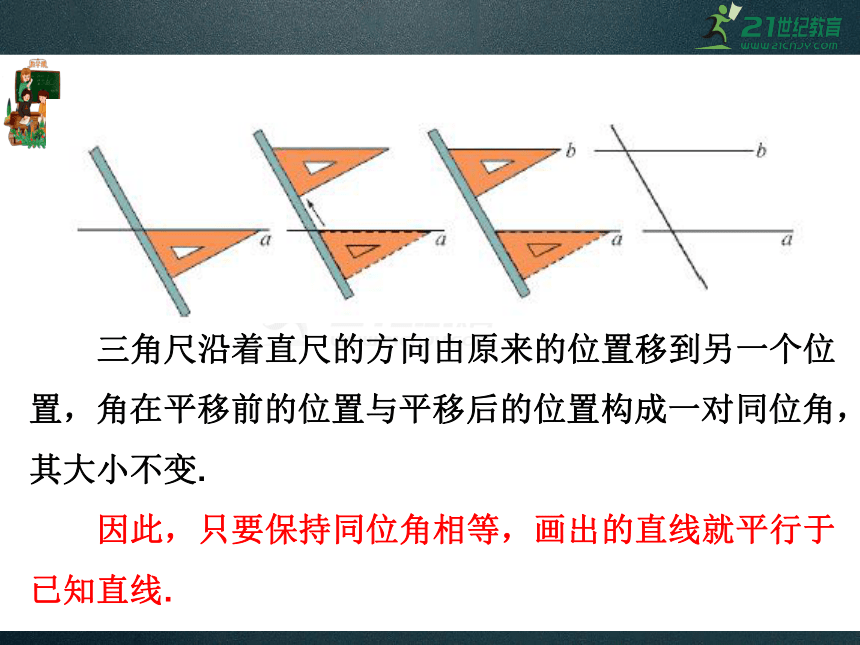
三角尺沿着直尺的方向由原来的位置移到另一个位置,角在平移前的位置与平移后的位置构成一对同位角,其大小不变.
因此,只要保持同位角相等,画出的直线就平行于已知直线.
一般地,判断两直线平行有下面的方法:
两条直线被第三条直线所截 ,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
应用格式:
∵∠1=∠2(已知)
∴a∥b (同位角相等,两直线平行)
1
2
l2
l1
A
B
总结归纳
1 如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD
C.AD∥EF D.EF∥BC
导引:要判定哪两条直线平行,就是要确定∠1,∠2
是哪两条直线被第三条直线
截得到的同位角, 即找出∠1,
∠2除公共边所在直线外的另
两边所在直线.
C
练一练
思考:两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
如图,由 3= 2,可推出a//b吗?如何推出?
解: ∵ 1= 3(已知)
3= 2(对顶角相等)
1= 2
a//b(同位角相等,两直线平行)
2
b
a
1
3
两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行。
2
b
a
1
3
∵∠3=∠2(已知)
∴a∥b (内错角相等,两直线平行)
应用格式:
总结归纳
如图,如果 1+ 2=180° 能判定a//b吗
c
解:能,
∵ 1+ 2=1800(已知)
1+ 3=1800(邻补角定义)
2= 3(同角的补角相等)
a//b (同位角相等,两直线平行)
2
b
a
1
3
两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
应用格式:
2
b
a
1
3
∵∠1+∠2=180°(已知)
∴a∥b (内错角相等,两直线平行)
总结归纳
例1. 如图,直线a、b被直线l所截,已知∠1=115°,∠2=115°,那么a∥b吗?为什么?
a
b
l
3
2
1
解: ∵
∴ ∠2= ∠1 (等量代换),
∴ a∥b (内错角相等,两直线平行).
∠1 =115°,∠2=115°
(已知),
例题精析
例2 如图,在四边形ABCD中,已知∠B=60°,
∠C=120°,AB
与CD平行吗?AD
与BC平行吗?
解: ∵∠B=60°, ∠C=120°(已知),
∴∠B+∠C=180°(等式的性质),
∴AB∥CD(同旁内角互补,两直线平行).
本题中,根据已知条件,无法判定AD与
BC是否平行.
例3 如图,在同一平面内,直线CD、EF均与直
线AB垂直,D、F为垂足.试判断CD与EF是
否平行.
解:∵ CD ⊥AB,EF⊥AB(已知),
∴∠ADC=∠AFE=90°,
∴ CD∥ EF(同位角相等,两直线平行).
思考:在同一平面内,两条直线垂直于同一条直线,这两条直线平行吗?为什么?
a
b
c
1
2
垂直于同一条直线的两条直线平行.
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(同位角相等,两直线平行)
你还能利用其他方法说明b//c吗?
平行线判定:垂直于同一条直线的两条直线平行.
判定两直线平行的方法:
方法一:平行线的定义:在同一平面内,不相交的两
条直线就是平行线.
方法二:如果两条直线都和第三条直线平行,那么这
两条直线也互相平行.
方法三:同位角相等,两直线平行.
方法四:内错角相等,两直线平行.
方法五:同旁内角互补,两直线平行.
方法六:在同一平面内,垂直于同一条直线的两条直
线平行.
总结归纳
1.如图,可以确定AB∥CE的条件是( )
A.∠2=∠B
B. ∠1=∠A
C. ∠3=∠B
D. ∠3=∠A
C
1
2
3
A
E
B
C
D
随堂练习
2.如图,∠AEF=∠EFC,则下列结论中正 确
的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF D.EF∥BC
导引:∠AEF和∠EFC是直线AB,CD被直线EF所截
得到的内错角,根据“内错角相等,两直线平
行”可知,AB∥CD.
B
3.如图,CD平分∠ACE,且∠B=∠ACD,可以得出的结论是( )
A.AD∥BC B.AB∥CD
C.CA平分∠BCD D.AC平分∠BAD
4.如图,已知∠1=30°,∠2或∠3满足条件___________________,
则a//b.
2
1
3
a
b
c
∠2=150°或∠3=30°
5.如图.(1)从∠1=∠4,可以推出 ∥ ,
理由是 .
(2)从∠ABC +∠ =180°,可以推出AB∥CD ,
理由是 .
A
B
C
D
1
2
3
4
5
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
(3)从∠ =∠ ,可以推出AD∥BC,
理由是 .
(4)从∠5=∠ ,可以推出AB∥CD,
理由是 .
2
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
A
B
C
D
1
2
3
4
5
6.如图,已知∠1= ∠3,AC平分∠DAB你能判断那两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
解: AB∥CD.
理由:
∵ AC平分∠DAB(已知)
∴ ∠1=∠2(角平分线定义)
又∵ ∠1= ∠3(已知)
∴ ∠2=∠3(等量代换)
∴ AB∥CD( 内错角相等,两直线平行)
7.如图,在四边形ABCD中,已知∠B=60°,∠C=120°,AB与CD平行吗?AD与BC平行吗?
解: AB∥CD.
∵ ∠B=60°,∠C=120°(已知),
∴ ∠B+∠C=180°,
∴ AB∥CD(同旁内角互补,两直线平行).
AD与BC不一定平行.
8.如图,已知∠ADE=60°,DF平分∠ADE,
∠1=30°,试
说明:DF∥BE.
导引:要想说明DF∥BE,可通过说明∠1=∠EDF
来实现,∵∠1=30°,∴只需求出∠EDF=
30°,而这个结论可通过DF是∠ADE的平分
线来求得.
解:∵DF平分∠ADE(已知),
∴∠EDF= ∠ADE(角平分线的定义).
又∵∠ADE=60°,
∴∠EDF=30°.
又∵∠1=30°(已知),
∴∠EDF=∠1,
∴DF∥BE(内错角相等,两直线平行).
9.如图所示,∠B=∠D,
∠CEF=∠A.试问CD
与EF平行吗?为什么?
导引:1.要说明CD∥EF,我们无法找出相等的同位
角、内错角,也无法说明其同旁内角互补,
因此需找第三条直线与它们平行(即AB∥CD,
AB∥EF),这都能由已知∠B=∠D,∠CEF
=∠A说明.
2.由已知∠B=∠D,∠CEF=∠A很容易就能得出
AB∥CD及EF∥AB,再由如果两条直线都和第三
条直线平行,那么这两条直线也互相平行就可得到
CD∥EF.
解:CD∥EF,理由:
∵∠B=∠D,∴AB∥CD(内错角相等,两直线平行).
∵∠CEF=∠A,
∴EF∥AB(同位角相等,两直线平行).
∴CD∥EF(平行于同一条直线的两条直线平行).
四、课堂小结
平行线判定的几种方法是什么?
通过今天的学习,你想进一步探究的问题是什么?
四、课堂小结
平行线的判定示意图
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
数量关系
位置关系
五、布置作业
教材第174页练习第1、2、3、4题.
https://www.21cnjy.com/help/help_extract.php
华师大版 初中数学
5.2 平行线
第2课时 平行线的判定
学习目标
1.掌握平行线的三种判定方法,会运用判定方法来判断两条
直线是否平行;(重点)
2.能够根据平行线的判定方法进行简单的推理.
问题1 两条直线的位置关系有哪几种?
问题2 怎样的两条直线平行?
问题3 上节课你学了平行线的哪些内容?
相交(包括垂直)和平行两种.
在同一平面内,不相交的两条直线平行.
如果两条直线都与第三条直线平行,那么这两条直线互相平行.
经过直线外一点,有且只有一条直线与已知直线平行.
回顾与思考
思考
根据平行线的定义,如果平面内的两条直线不相交,就可以判断这两条直线平行.但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据两条直线是否平行,那么有没有其他判定方法呢?
●
一、放
二、靠
三、推
四、画
我们已经学习过用三角尺和直尺画平行线的方法.
平行线的判定
●
问题 在画图过程中,三角尺起着什么样的作用?
思考 要判断两直线平行,你有办法了吗?
b
A
2
1
a
B
(1)这样的画法可以看作是怎样的图形变换?
(2)画图过程中,什么角始终保持相等?
(3)直线a,b位置关系如何?
问题
(4)请将其最初和最终的特殊位置抽象成几何图形:
1
2
l2
l1
A
B
(5) 由上面的操作过程,你能发现判定两直线平行的方法吗?
三角尺沿着直尺的方向由原来的位置移到另一个位置,角在平移前的位置与平移后的位置构成一对同位角,其大小不变.
因此,只要保持同位角相等,画出的直线就平行于已知直线.
一般地,判断两直线平行有下面的方法:
两条直线被第三条直线所截 ,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
应用格式:
∵∠1=∠2(已知)
∴a∥b (同位角相等,两直线平行)
1
2
l2
l1
A
B
总结归纳
1 如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD
C.AD∥EF D.EF∥BC
导引:要判定哪两条直线平行,就是要确定∠1,∠2
是哪两条直线被第三条直线
截得到的同位角, 即找出∠1,
∠2除公共边所在直线外的另
两边所在直线.
C
练一练
思考:两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
如图,由 3= 2,可推出a//b吗?如何推出?
解: ∵ 1= 3(已知)
3= 2(对顶角相等)
1= 2
a//b(同位角相等,两直线平行)
2
b
a
1
3
两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行。
2
b
a
1
3
∵∠3=∠2(已知)
∴a∥b (内错角相等,两直线平行)
应用格式:
总结归纳
如图,如果 1+ 2=180° 能判定a//b吗
c
解:能,
∵ 1+ 2=1800(已知)
1+ 3=1800(邻补角定义)
2= 3(同角的补角相等)
a//b (同位角相等,两直线平行)
2
b
a
1
3
两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
应用格式:
2
b
a
1
3
∵∠1+∠2=180°(已知)
∴a∥b (内错角相等,两直线平行)
总结归纳
例1. 如图,直线a、b被直线l所截,已知∠1=115°,∠2=115°,那么a∥b吗?为什么?
a
b
l
3
2
1
解: ∵
∴ ∠2= ∠1 (等量代换),
∴ a∥b (内错角相等,两直线平行).
∠1 =115°,∠2=115°
(已知),
例题精析
例2 如图,在四边形ABCD中,已知∠B=60°,
∠C=120°,AB
与CD平行吗?AD
与BC平行吗?
解: ∵∠B=60°, ∠C=120°(已知),
∴∠B+∠C=180°(等式的性质),
∴AB∥CD(同旁内角互补,两直线平行).
本题中,根据已知条件,无法判定AD与
BC是否平行.
例3 如图,在同一平面内,直线CD、EF均与直
线AB垂直,D、F为垂足.试判断CD与EF是
否平行.
解:∵ CD ⊥AB,EF⊥AB(已知),
∴∠ADC=∠AFE=90°,
∴ CD∥ EF(同位角相等,两直线平行).
思考:在同一平面内,两条直线垂直于同一条直线,这两条直线平行吗?为什么?
a
b
c
1
2
垂直于同一条直线的两条直线平行.
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(同位角相等,两直线平行)
你还能利用其他方法说明b//c吗?
平行线判定:垂直于同一条直线的两条直线平行.
判定两直线平行的方法:
方法一:平行线的定义:在同一平面内,不相交的两
条直线就是平行线.
方法二:如果两条直线都和第三条直线平行,那么这
两条直线也互相平行.
方法三:同位角相等,两直线平行.
方法四:内错角相等,两直线平行.
方法五:同旁内角互补,两直线平行.
方法六:在同一平面内,垂直于同一条直线的两条直
线平行.
总结归纳
1.如图,可以确定AB∥CE的条件是( )
A.∠2=∠B
B. ∠1=∠A
C. ∠3=∠B
D. ∠3=∠A
C
1
2
3
A
E
B
C
D
随堂练习
2.如图,∠AEF=∠EFC,则下列结论中正 确
的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF D.EF∥BC
导引:∠AEF和∠EFC是直线AB,CD被直线EF所截
得到的内错角,根据“内错角相等,两直线平
行”可知,AB∥CD.
B
3.如图,CD平分∠ACE,且∠B=∠ACD,可以得出的结论是( )
A.AD∥BC B.AB∥CD
C.CA平分∠BCD D.AC平分∠BAD
4.如图,已知∠1=30°,∠2或∠3满足条件___________________,
则a//b.
2
1
3
a
b
c
∠2=150°或∠3=30°
5.如图.(1)从∠1=∠4,可以推出 ∥ ,
理由是 .
(2)从∠ABC +∠ =180°,可以推出AB∥CD ,
理由是 .
A
B
C
D
1
2
3
4
5
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
(3)从∠ =∠ ,可以推出AD∥BC,
理由是 .
(4)从∠5=∠ ,可以推出AB∥CD,
理由是 .
2
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
A
B
C
D
1
2
3
4
5
6.如图,已知∠1= ∠3,AC平分∠DAB你能判断那两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
解: AB∥CD.
理由:
∵ AC平分∠DAB(已知)
∴ ∠1=∠2(角平分线定义)
又∵ ∠1= ∠3(已知)
∴ ∠2=∠3(等量代换)
∴ AB∥CD( 内错角相等,两直线平行)
7.如图,在四边形ABCD中,已知∠B=60°,∠C=120°,AB与CD平行吗?AD与BC平行吗?
解: AB∥CD.
∵ ∠B=60°,∠C=120°(已知),
∴ ∠B+∠C=180°,
∴ AB∥CD(同旁内角互补,两直线平行).
AD与BC不一定平行.
8.如图,已知∠ADE=60°,DF平分∠ADE,
∠1=30°,试
说明:DF∥BE.
导引:要想说明DF∥BE,可通过说明∠1=∠EDF
来实现,∵∠1=30°,∴只需求出∠EDF=
30°,而这个结论可通过DF是∠ADE的平分
线来求得.
解:∵DF平分∠ADE(已知),
∴∠EDF= ∠ADE(角平分线的定义).
又∵∠ADE=60°,
∴∠EDF=30°.
又∵∠1=30°(已知),
∴∠EDF=∠1,
∴DF∥BE(内错角相等,两直线平行).
9.如图所示,∠B=∠D,
∠CEF=∠A.试问CD
与EF平行吗?为什么?
导引:1.要说明CD∥EF,我们无法找出相等的同位
角、内错角,也无法说明其同旁内角互补,
因此需找第三条直线与它们平行(即AB∥CD,
AB∥EF),这都能由已知∠B=∠D,∠CEF
=∠A说明.
2.由已知∠B=∠D,∠CEF=∠A很容易就能得出
AB∥CD及EF∥AB,再由如果两条直线都和第三
条直线平行,那么这两条直线也互相平行就可得到
CD∥EF.
解:CD∥EF,理由:
∵∠B=∠D,∴AB∥CD(内错角相等,两直线平行).
∵∠CEF=∠A,
∴EF∥AB(同位角相等,两直线平行).
∴CD∥EF(平行于同一条直线的两条直线平行).
四、课堂小结
平行线判定的几种方法是什么?
通过今天的学习,你想进一步探究的问题是什么?
四、课堂小结
平行线的判定示意图
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
数量关系
位置关系
五、布置作业
教材第174页练习第1、2、3、4题.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
