第三章 整式及其加减单元测试题一(含答案)
文档属性
| 名称 | 第三章 整式及其加减单元测试题一(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 492.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-11 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大版七年级上册数学第三章整式及其加减
单元测试一
学校:___________姓名:___________班级:___________
一、单选题
1.用代数式表示:a的2倍与3
的和.下列表示正确的是(
)
A.2a-3
B.2a+3
C.2(a-3)
D.2(a+3)
2.小红要购买珠子串成一条手链,黑色珠子每个a元,白色珠子每个b元,要串成如图所示的手链,小红购买珠子应该花费(
)
A.(3a+4b)元
B.(4a+3b)元
C.4(a+b)元
D.3(a+b)元
3.2014年我省财政收入比2013年增长8.9%,2015年比2014年增长9.5%,若2013年和2015年我省财政收入分别为a亿元和b亿元,则a、b之间满足的关系式为( )
A.
B.
C.
D.
4.正方体的棱长为,当棱长增加时,体积增加了(
)
A.a3-x3
B.x3
C.(a+x)
3-a3
D.(a+x)
3-x3
5.如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长2b的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为( )
A.3a+2b
B.3a+4b
C.6a+2b
D.6a+4b
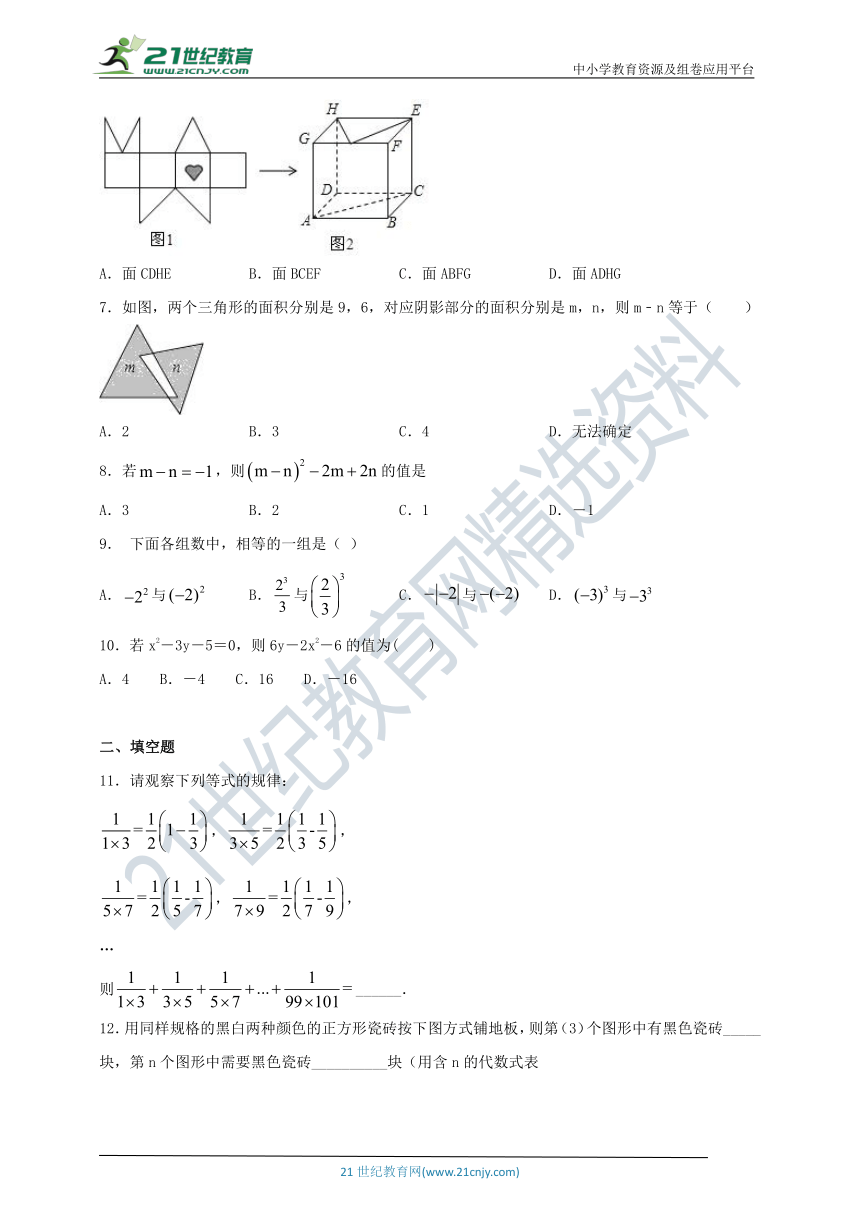
6.将图1围成图2的正方体,则图1中的红心“”标志所在的正方形是正方体中的( )
A.面CDHE
B.面BCEF
C.面ABFG
D.面ADHG
7.如图,两个三角形的面积分别是9,6,对应阴影部分的面积分别是m,n,则m﹣n等于( )
A.2
B.3
C.4
D.无法确定
8.若,则的值是
A.3
B.2
C.1
D.―1
9.
下面各组数中,相等的一组是(
)
A.与
B.与
C.与
D.与
10.若x2-3y-5=0,则6y-2x2-6的值为( )
A.4
B.-4
C.16
D.-16
二、填空题
11.请观察下列等式的规律:
,,
,,
…
则______.
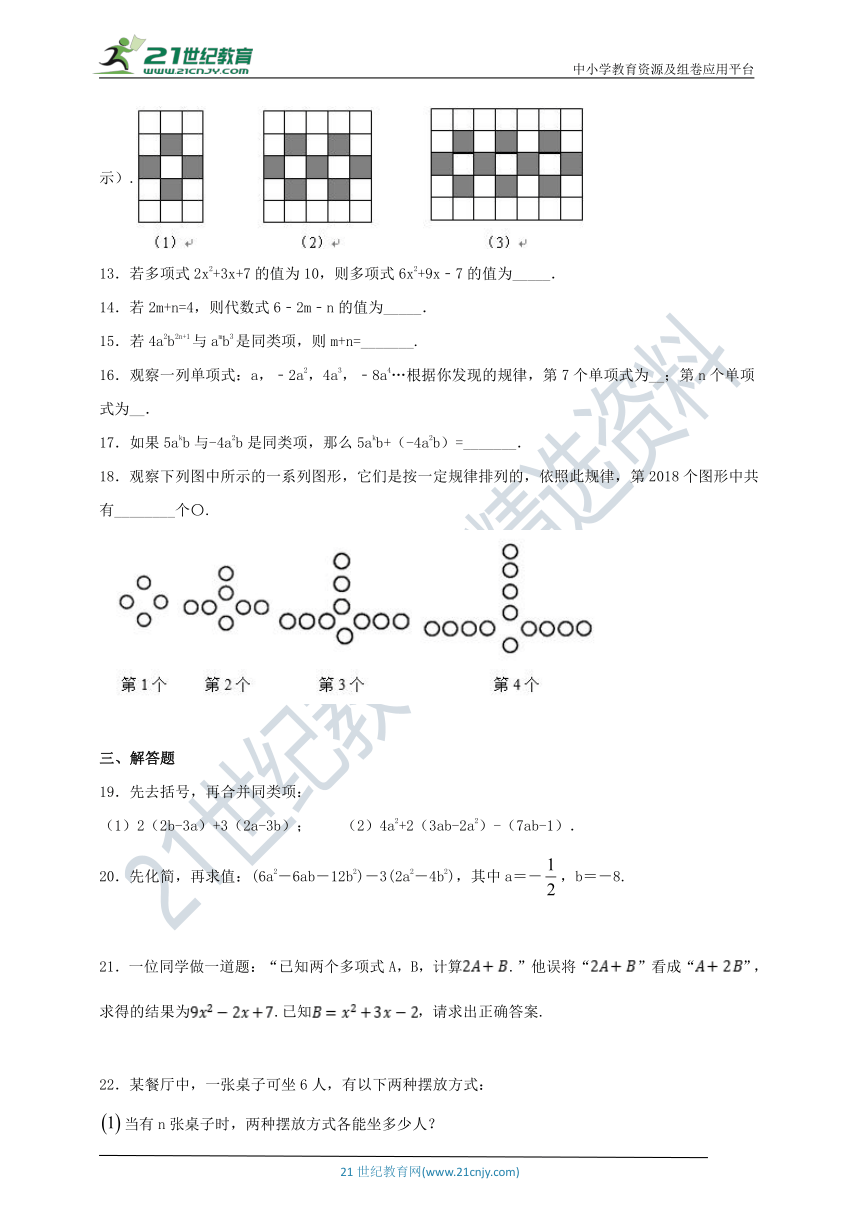
12.用同样规格的黑白两种颜色的正方形瓷砖按下图方式铺地板,则第(3)个图形中有黑色瓷砖_____块,第n个图形中需要黑色瓷砖__________块(用含n的代数式表示).
13.若多项式2x2+3x+7的值为10,则多项式6x2+9x﹣7的值为_____.
14.若2m+n=4,则代数式6﹣2m﹣n的值为_____.
15.若4a2b2n+1与amb3是同类项,则m+n=_______.
16.观察一列单项式:a,﹣2a2,4a3,﹣8a4…根据你发现的规律,第7个单项式为__;第n个单项式为__.
17.如果5akb与-4a2b是同类项,那么5akb+(-4a2b)=_______.
18.观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2018个图形中共有________个〇.
三、解答题
19.先去括号,再合并同类项:????????????????
(1)2(2b-3a)+3(2a-3b);
(2)4a2+2(3ab-2a2)-(7ab-1).
20.先化简,再求值:(6a2-6ab-12b2)-3(2a2-4b2),其中a=-,b=-8.
21.一位同学做一道题:“已知两个多项式A,B,计算.”他误将“”看成“”,求得的结果为.已知,请求出正确答案.
22.某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
当有n张桌子时,两种摆放方式各能坐多少人?
一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌为什么?
23.公安人员在破案时,常常根据案发现场作案人员留下的脚印推断犯人的身高,如果用表示脚印长度,表示身高,关系类似于.
(1)某人脚印长度为,则他的身高约为多少厘米?
(2)在某次案件中,抓获了两个可疑人员,一个身高为,另一个身高为,现场测量的脚印长度为,请你帮助侦察一下,哪个可疑人员的可能性更大?
24.小丽同学准备化简:(3x2﹣6x﹣8)﹣(x2﹣2x□6),算式中“□”是“+,﹣,×,÷”中的某一种运算符号.
(1)如果“□”是“×”,请你化简:(3x2﹣6x﹣8)﹣(x2﹣2x×6);
(2)若x2﹣2x﹣3=0,求(3x2﹣6x﹣8)﹣(x2﹣2x﹣6)的值;
(3)当x=1时,(3x2﹣6x﹣8)﹣(x2﹣2x□6)的结果是﹣8,请你通过计算说明“□”所代表的运算符号.
25.
将连续偶数2,4,6,…排成如下表格,用十字框框出5个数,问:
(1)十字框框出的5个数分别与框中间的数32有什么关系?
(2)5个数的和与32有什么关系?
(3)如果将十字框上下左右移动,仍框出5个数,这五个数还有这种规律吗?
(4)设中间数为a,用代数式表示十字框框出的5个数的和.
参考答案
1.B
【解析】
分析:a的2倍与3的和也就是用a乘2再加上3,列出代数式即可.
详解:“a的2倍与3
的和”是2a+3.
故选B.
点睛:此题考查列代数式,解决问题的关键是读懂题意,找到所求的量的数量关系,注意字母和数字相乘的简写方法.
2.A
【解析】
【分析】
直接利用两种颜色的珠子的价格进而求出手链的价格.
【详解】
解:∵黑色珠子每个a元,白色珠子每个b元,
∴要串成如图所示的手链,小红购买珠子应该花费为:3a+4b.
故选A.
【点睛】
本题考查列代数式,正确得出各种颜色珠子的数量是解题关键.
3.C
【解析】
【分析】
根据2013年我省财政收入和2014年我省财政收入比2013年增长8.9%,求出2014年我省财政收入,再根据出2015年比2014年增长9.5%,2015年我省财政收为b亿元,
即可得出a、b之间的关系式.
【详解】
∵2013年我省财政收入为a亿元,2014年我省财政收入比2013年增长8.9%,
∴2014年我省财政收入为a(1+8.9%)亿元,
∵2015年比2014年增长9.5%,2015年我省财政收为b亿元,
∴2015年我省财政收为b=a(1+8.9%)(1+9.5%);
故选C.
【点睛】
此题考查了列代数式,关键是根据题意求出2014年我省财政的收入,是一道基础题.
4.C
【解析】
本题考查正方体的体积公式
根据正方体的体积公式,用变化后的正方体体积减去原来的正方体体积即得答案.
根据题意,正方体的体积增加了(a+x)3-a3.故选C.
列代数式的关键是掌握好正方体的体积公式.
5.A
【解析】
【分析】
根据这块矩形较长的边长=边长为3a的正方形的边长-边长为2b的小正方形的边长+边长为2b的小正方形的边长的2倍代入数据即可.
【详解】
依题意有:3a﹣2b+2b×2=3a﹣2b+4b=3a+2b.
故这块矩形较长的边长为3a+2b.故选A.
【点睛】
本题主要考查矩形、正方形和整式的运算,熟读题目,理解题意,清楚题中的等量关系是解答本题的关键.
6.A
【解析】
试题分析:由平面图形的折叠及正方体的展开图解题.注意找准红心“”标志所在的相邻面.
解:由图1中的红心“”标志,
可知它与等边三角形相邻,折叠成正方体是正方体中的面CDHE.
故选A.
考点:展开图折叠成几何体.
7.B
【解析】
试题分析:设空白出图形的面积为x,根据题意得:m+x=9,n+x=6,则m﹣n=9﹣6=3.故选B.
考点:三角形的面积.
8.A
【解析】
试题分析:所求式子后两项提取﹣2变形后,将整体代入计算即可求出值:
∵,
∴.
故选A.
9.D
【解析】
试题分析:由-12=-1,而(-1)2=1,故A不正确;=,而=,故B不正确;由-=-2,而-(-2)=2,故C不正确;由=-27,且-=-27,故正确.
故选D
考点:幂的运算
10.D
【解析】
试题分析:由x2﹣3y﹣5=0可得x2﹣3y=5,所以6y﹣2x2﹣6=﹣2(x2﹣3y)﹣6=﹣2×5﹣6=﹣16,故答案选D.
考点:整体思想.
11.
【解析】
试题解析:
=
=
=
=
=.
12.10;3n+1
【解析】
【分析】
有图可知每一个图的黑色正方形都比前一个图多三个,一次写出图形n与黑色正方形的个数的关系式即可.
【详解】
解:本题考查的是规律探究问题.从图形观察每增加一个图形,黑色正方形瓷砖就增加3块,第一个黑色瓷砖有3块,则第3个图形黑色瓷砖有10块,第n个图形瓷砖有4+3(n-1)=3n+1(块).
【点睛】
分析几何模型,进行合理的运算,找到图形的变换的规律,并给出合理的数学模型.
13.2
【解析】
试题分析:由题意可得:2x2+3x+7=10,所以移项得:2x2+3x=10-7=3,所求多项式转化为:6x2+9x﹣7=3(6x2+9x)-7=3×3-7=9-7=2,故答案为2.
考点:求多项式的值.
14.2
【解析】
【分析】
将6-2m-n化成6-(2m+n)代值即可得出结论.
【详解】
∵2m+n=4,
∴6-2m-n=6-(2m+n)=6-4=2,
故答案为2.
【点睛】
此题是代数式求值问题,利用整体代入是解本题的关键.
15.3
【解析】
∵4a2b2n+1与amb3是同类项,
∴,∴,
∴m+n=3,
故答案为:3.
16.
【解析】
【分析】
本题须先通过观察已知条件,找出这列单项式的规律即可求出结果.
【详解】
根据观察可得
第7个单项式为64a7
第n个单项式为
(-2)n-1an.
故答案为64a7,(-2)n-1an.
【点睛】
本题主要考查了单项式的有关知识,在解题时要能通过观察得出规律是本题的关键.
17.a2b
【解析】
【分析】
根据同类项:所含字母相同,并且相同字母的指数也相同,可得出k的值,再合并同类项即可.
【详解】
∵5akb与-4a2b是同类项,
∴k=2,
∴5akb+(-4a2b)=5a2b-4a2b=a2b.
故答案为a2b.
【点睛】
本题考查了同类项的定义,关键是掌握同类项定义中的两个“相同”:相同字母的指数相同,是易混点,因此成了中考的常考点.
18.6055
【解析】
【分析】
每个图形的最下面一排都是1,另外三面随着图形的增加,每面的个数也增加,据此可得出规律,则可求得答案.
【详解】
解:
观察图形可知:
第1个图形共有:1+1×3,
第2个图形共有:1+2×3,
第3个图形共有:1+3×3,
…,
第n个图形共有:1+3n,
∴第2018个图形共有1+3×2018=6055,
故答案为6055.
【点睛】
本题为规律型题目,找出图形的变化规律是解题的关键,注意观察图形的变化.
19.(1)-5b;(2)-ab+1
【解析】
【分析】
(1)根据括号前是正号去括号不变号,括号前是负号去掉括号要变号,可去掉括号,根据合并同类项,可得答案;
(2)根据括号前是正号去括号不变号,括号前是负号去掉括号要变号,可去掉括号,根据合并同类项,可得答案;
【详解】
(1)2(2b-3a)+3(2a-3b)=4b-6a+6a-9b=-5b;
(2)4a2+2(3ab-2a2)-(7ab-1)=4a2+6ab-4a2-7ab+1=-ab+1.
【点睛】
本题考查了去括号与添括号,合并同类项,括号前是正号去掉括号不变号,括号前是负号去掉括号要变号.
20.-24.
【解析】
【分析】
原式去括号合并得到最简结果,把a与b的值代入计算即可求出值.
【详解】
原式=6a2﹣6ab﹣12b2﹣6a2+12b2=﹣6ab,
当a=﹣,b=﹣8时,原式=﹣6×(﹣)×(﹣8)=﹣24.
【点睛】
本题考查了整式的加减﹣化简求值,熟练掌握运算法则是解答本题的关键.
21.
【解析】
【分析】
根据题意列出式子,先求出A表示的多项式,然后再求2A+B.
【详解】
解:由,,
得.
所以.
【点睛】
本题考查整式的加减运算,整式的加减运算实际上就是去括号、合并同类项,这是各地中考的常考点.根据题中的关系可先求出A,进一步求得2A+B.
22.(1)第一种方式坐的人数:4n+2,第二种方式坐的人数:2n+4;(2)选第一种方式,理由见解析.
【解析】
解:(1)第一种中,有一张桌子时有6人,后边多一张桌子多4人.
即有张桌子时,有.
第二种中,有一张桌子时有6人,后边多一张桌子多2人,即.
(2)打算用第一种摆放方式来摆放餐桌.
因为当时,用第一种方式摆放餐桌:,
用第二种方式摆放餐桌:,
所以选用第一种摆放方式.
23.【答案】(1)168.43cm;(2)身高为的可疑人员可能性更大
【解析】(1)当时,
,
所以他的身高约为;
(2)当脚印的长度为时,
,
因为更接近,所以身高为的可疑人员可能性更大.
24.【答案】(1)2x2+6x﹣8;(2)4;(3)□处应为“﹣”.
【解析】(1)(3x2﹣6x﹣8)﹣(x2﹣2x×6)
=(3x2﹣6x﹣8)﹣(x2﹣12x)
=3x2﹣6x﹣8﹣x2+12x
=2x2+6x﹣8;
(2)(3x2﹣6x﹣8)﹣(x2﹣2x﹣6)
=3x2﹣6x﹣8﹣x2+2x+6
=2x2﹣4x﹣2,
∵x2﹣2x﹣3=0,
∴x2﹣2x=3,
∴2x2﹣4x﹣2=2(x2﹣2x)﹣2=6﹣2=4;
(3)“□”所代表的运算符号是“﹣”,
当x=1时,原式=(3﹣6﹣8)﹣(1﹣2□6),
∴﹣11﹣(1+2□6)=﹣8,
整理得:1+2□6=﹣3,
∴2□6=﹣4
∴即□处应为“﹣”.
25.解:(1)十字框框出的5个数,上面的数比中间的数小12,下面的数比中间的数大12,左面的数比中间的数小2,右面的数比中间的数大2.
(2)五个数之和为20+30+32+34+44=160.
160=32×5恰为中间的数的5倍.
(3)仍有这种规律.
(4)设中间数为a,则5个数之和为(a-12)+(a-2)+a+(a+2)+(a+12)=5a.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
北师大版七年级上册数学第三章整式及其加减
单元测试一
学校:___________姓名:___________班级:___________
一、单选题
1.用代数式表示:a的2倍与3
的和.下列表示正确的是(
)
A.2a-3
B.2a+3
C.2(a-3)
D.2(a+3)
2.小红要购买珠子串成一条手链,黑色珠子每个a元,白色珠子每个b元,要串成如图所示的手链,小红购买珠子应该花费(
)
A.(3a+4b)元
B.(4a+3b)元
C.4(a+b)元
D.3(a+b)元
3.2014年我省财政收入比2013年增长8.9%,2015年比2014年增长9.5%,若2013年和2015年我省财政收入分别为a亿元和b亿元,则a、b之间满足的关系式为( )
A.
B.
C.
D.
4.正方体的棱长为,当棱长增加时,体积增加了(
)
A.a3-x3
B.x3
C.(a+x)
3-a3
D.(a+x)
3-x3
5.如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长2b的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为( )
A.3a+2b
B.3a+4b
C.6a+2b
D.6a+4b
6.将图1围成图2的正方体,则图1中的红心“”标志所在的正方形是正方体中的( )
A.面CDHE
B.面BCEF
C.面ABFG
D.面ADHG
7.如图,两个三角形的面积分别是9,6,对应阴影部分的面积分别是m,n,则m﹣n等于( )
A.2
B.3
C.4
D.无法确定
8.若,则的值是
A.3
B.2
C.1
D.―1
9.
下面各组数中,相等的一组是(
)
A.与
B.与
C.与
D.与
10.若x2-3y-5=0,则6y-2x2-6的值为( )
A.4
B.-4
C.16
D.-16
二、填空题
11.请观察下列等式的规律:
,,
,,
…
则______.
12.用同样规格的黑白两种颜色的正方形瓷砖按下图方式铺地板,则第(3)个图形中有黑色瓷砖_____块,第n个图形中需要黑色瓷砖__________块(用含n的代数式表示).
13.若多项式2x2+3x+7的值为10,则多项式6x2+9x﹣7的值为_____.
14.若2m+n=4,则代数式6﹣2m﹣n的值为_____.
15.若4a2b2n+1与amb3是同类项,则m+n=_______.
16.观察一列单项式:a,﹣2a2,4a3,﹣8a4…根据你发现的规律,第7个单项式为__;第n个单项式为__.
17.如果5akb与-4a2b是同类项,那么5akb+(-4a2b)=_______.
18.观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2018个图形中共有________个〇.
三、解答题
19.先去括号,再合并同类项:????????????????
(1)2(2b-3a)+3(2a-3b);
(2)4a2+2(3ab-2a2)-(7ab-1).
20.先化简,再求值:(6a2-6ab-12b2)-3(2a2-4b2),其中a=-,b=-8.
21.一位同学做一道题:“已知两个多项式A,B,计算.”他误将“”看成“”,求得的结果为.已知,请求出正确答案.
22.某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
当有n张桌子时,两种摆放方式各能坐多少人?
一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌为什么?
23.公安人员在破案时,常常根据案发现场作案人员留下的脚印推断犯人的身高,如果用表示脚印长度,表示身高,关系类似于.
(1)某人脚印长度为,则他的身高约为多少厘米?
(2)在某次案件中,抓获了两个可疑人员,一个身高为,另一个身高为,现场测量的脚印长度为,请你帮助侦察一下,哪个可疑人员的可能性更大?
24.小丽同学准备化简:(3x2﹣6x﹣8)﹣(x2﹣2x□6),算式中“□”是“+,﹣,×,÷”中的某一种运算符号.
(1)如果“□”是“×”,请你化简:(3x2﹣6x﹣8)﹣(x2﹣2x×6);
(2)若x2﹣2x﹣3=0,求(3x2﹣6x﹣8)﹣(x2﹣2x﹣6)的值;
(3)当x=1时,(3x2﹣6x﹣8)﹣(x2﹣2x□6)的结果是﹣8,请你通过计算说明“□”所代表的运算符号.
25.
将连续偶数2,4,6,…排成如下表格,用十字框框出5个数,问:
(1)十字框框出的5个数分别与框中间的数32有什么关系?
(2)5个数的和与32有什么关系?
(3)如果将十字框上下左右移动,仍框出5个数,这五个数还有这种规律吗?
(4)设中间数为a,用代数式表示十字框框出的5个数的和.
参考答案
1.B
【解析】
分析:a的2倍与3的和也就是用a乘2再加上3,列出代数式即可.
详解:“a的2倍与3
的和”是2a+3.
故选B.
点睛:此题考查列代数式,解决问题的关键是读懂题意,找到所求的量的数量关系,注意字母和数字相乘的简写方法.
2.A
【解析】
【分析】
直接利用两种颜色的珠子的价格进而求出手链的价格.
【详解】
解:∵黑色珠子每个a元,白色珠子每个b元,
∴要串成如图所示的手链,小红购买珠子应该花费为:3a+4b.
故选A.
【点睛】
本题考查列代数式,正确得出各种颜色珠子的数量是解题关键.
3.C
【解析】
【分析】
根据2013年我省财政收入和2014年我省财政收入比2013年增长8.9%,求出2014年我省财政收入,再根据出2015年比2014年增长9.5%,2015年我省财政收为b亿元,
即可得出a、b之间的关系式.
【详解】
∵2013年我省财政收入为a亿元,2014年我省财政收入比2013年增长8.9%,
∴2014年我省财政收入为a(1+8.9%)亿元,
∵2015年比2014年增长9.5%,2015年我省财政收为b亿元,
∴2015年我省财政收为b=a(1+8.9%)(1+9.5%);
故选C.
【点睛】
此题考查了列代数式,关键是根据题意求出2014年我省财政的收入,是一道基础题.
4.C
【解析】
本题考查正方体的体积公式
根据正方体的体积公式,用变化后的正方体体积减去原来的正方体体积即得答案.
根据题意,正方体的体积增加了(a+x)3-a3.故选C.
列代数式的关键是掌握好正方体的体积公式.
5.A
【解析】
【分析】
根据这块矩形较长的边长=边长为3a的正方形的边长-边长为2b的小正方形的边长+边长为2b的小正方形的边长的2倍代入数据即可.
【详解】
依题意有:3a﹣2b+2b×2=3a﹣2b+4b=3a+2b.
故这块矩形较长的边长为3a+2b.故选A.
【点睛】
本题主要考查矩形、正方形和整式的运算,熟读题目,理解题意,清楚题中的等量关系是解答本题的关键.
6.A
【解析】
试题分析:由平面图形的折叠及正方体的展开图解题.注意找准红心“”标志所在的相邻面.
解:由图1中的红心“”标志,
可知它与等边三角形相邻,折叠成正方体是正方体中的面CDHE.
故选A.
考点:展开图折叠成几何体.
7.B
【解析】
试题分析:设空白出图形的面积为x,根据题意得:m+x=9,n+x=6,则m﹣n=9﹣6=3.故选B.
考点:三角形的面积.
8.A
【解析】
试题分析:所求式子后两项提取﹣2变形后,将整体代入计算即可求出值:
∵,
∴.
故选A.
9.D
【解析】
试题分析:由-12=-1,而(-1)2=1,故A不正确;=,而=,故B不正确;由-=-2,而-(-2)=2,故C不正确;由=-27,且-=-27,故正确.
故选D
考点:幂的运算
10.D
【解析】
试题分析:由x2﹣3y﹣5=0可得x2﹣3y=5,所以6y﹣2x2﹣6=﹣2(x2﹣3y)﹣6=﹣2×5﹣6=﹣16,故答案选D.
考点:整体思想.
11.
【解析】
试题解析:
=
=
=
=
=.
12.10;3n+1
【解析】
【分析】
有图可知每一个图的黑色正方形都比前一个图多三个,一次写出图形n与黑色正方形的个数的关系式即可.
【详解】
解:本题考查的是规律探究问题.从图形观察每增加一个图形,黑色正方形瓷砖就增加3块,第一个黑色瓷砖有3块,则第3个图形黑色瓷砖有10块,第n个图形瓷砖有4+3(n-1)=3n+1(块).
【点睛】
分析几何模型,进行合理的运算,找到图形的变换的规律,并给出合理的数学模型.
13.2
【解析】
试题分析:由题意可得:2x2+3x+7=10,所以移项得:2x2+3x=10-7=3,所求多项式转化为:6x2+9x﹣7=3(6x2+9x)-7=3×3-7=9-7=2,故答案为2.
考点:求多项式的值.
14.2
【解析】
【分析】
将6-2m-n化成6-(2m+n)代值即可得出结论.
【详解】
∵2m+n=4,
∴6-2m-n=6-(2m+n)=6-4=2,
故答案为2.
【点睛】
此题是代数式求值问题,利用整体代入是解本题的关键.
15.3
【解析】
∵4a2b2n+1与amb3是同类项,
∴,∴,
∴m+n=3,
故答案为:3.
16.
【解析】
【分析】
本题须先通过观察已知条件,找出这列单项式的规律即可求出结果.
【详解】
根据观察可得
第7个单项式为64a7
第n个单项式为
(-2)n-1an.
故答案为64a7,(-2)n-1an.
【点睛】
本题主要考查了单项式的有关知识,在解题时要能通过观察得出规律是本题的关键.
17.a2b
【解析】
【分析】
根据同类项:所含字母相同,并且相同字母的指数也相同,可得出k的值,再合并同类项即可.
【详解】
∵5akb与-4a2b是同类项,
∴k=2,
∴5akb+(-4a2b)=5a2b-4a2b=a2b.
故答案为a2b.
【点睛】
本题考查了同类项的定义,关键是掌握同类项定义中的两个“相同”:相同字母的指数相同,是易混点,因此成了中考的常考点.
18.6055
【解析】
【分析】
每个图形的最下面一排都是1,另外三面随着图形的增加,每面的个数也增加,据此可得出规律,则可求得答案.
【详解】
解:
观察图形可知:
第1个图形共有:1+1×3,
第2个图形共有:1+2×3,
第3个图形共有:1+3×3,
…,
第n个图形共有:1+3n,
∴第2018个图形共有1+3×2018=6055,
故答案为6055.
【点睛】
本题为规律型题目,找出图形的变化规律是解题的关键,注意观察图形的变化.
19.(1)-5b;(2)-ab+1
【解析】
【分析】
(1)根据括号前是正号去括号不变号,括号前是负号去掉括号要变号,可去掉括号,根据合并同类项,可得答案;
(2)根据括号前是正号去括号不变号,括号前是负号去掉括号要变号,可去掉括号,根据合并同类项,可得答案;
【详解】
(1)2(2b-3a)+3(2a-3b)=4b-6a+6a-9b=-5b;
(2)4a2+2(3ab-2a2)-(7ab-1)=4a2+6ab-4a2-7ab+1=-ab+1.
【点睛】
本题考查了去括号与添括号,合并同类项,括号前是正号去掉括号不变号,括号前是负号去掉括号要变号.
20.-24.
【解析】
【分析】
原式去括号合并得到最简结果,把a与b的值代入计算即可求出值.
【详解】
原式=6a2﹣6ab﹣12b2﹣6a2+12b2=﹣6ab,
当a=﹣,b=﹣8时,原式=﹣6×(﹣)×(﹣8)=﹣24.
【点睛】
本题考查了整式的加减﹣化简求值,熟练掌握运算法则是解答本题的关键.
21.
【解析】
【分析】
根据题意列出式子,先求出A表示的多项式,然后再求2A+B.
【详解】
解:由,,
得.
所以.
【点睛】
本题考查整式的加减运算,整式的加减运算实际上就是去括号、合并同类项,这是各地中考的常考点.根据题中的关系可先求出A,进一步求得2A+B.
22.(1)第一种方式坐的人数:4n+2,第二种方式坐的人数:2n+4;(2)选第一种方式,理由见解析.
【解析】
解:(1)第一种中,有一张桌子时有6人,后边多一张桌子多4人.
即有张桌子时,有.
第二种中,有一张桌子时有6人,后边多一张桌子多2人,即.
(2)打算用第一种摆放方式来摆放餐桌.
因为当时,用第一种方式摆放餐桌:,
用第二种方式摆放餐桌:,
所以选用第一种摆放方式.
23.【答案】(1)168.43cm;(2)身高为的可疑人员可能性更大
【解析】(1)当时,
,
所以他的身高约为;
(2)当脚印的长度为时,
,
因为更接近,所以身高为的可疑人员可能性更大.
24.【答案】(1)2x2+6x﹣8;(2)4;(3)□处应为“﹣”.
【解析】(1)(3x2﹣6x﹣8)﹣(x2﹣2x×6)
=(3x2﹣6x﹣8)﹣(x2﹣12x)
=3x2﹣6x﹣8﹣x2+12x
=2x2+6x﹣8;
(2)(3x2﹣6x﹣8)﹣(x2﹣2x﹣6)
=3x2﹣6x﹣8﹣x2+2x+6
=2x2﹣4x﹣2,
∵x2﹣2x﹣3=0,
∴x2﹣2x=3,
∴2x2﹣4x﹣2=2(x2﹣2x)﹣2=6﹣2=4;
(3)“□”所代表的运算符号是“﹣”,
当x=1时,原式=(3﹣6﹣8)﹣(1﹣2□6),
∴﹣11﹣(1+2□6)=﹣8,
整理得:1+2□6=﹣3,
∴2□6=﹣4
∴即□处应为“﹣”.
25.解:(1)十字框框出的5个数,上面的数比中间的数小12,下面的数比中间的数大12,左面的数比中间的数小2,右面的数比中间的数大2.
(2)五个数之和为20+30+32+34+44=160.
160=32×5恰为中间的数的5倍.
(3)仍有这种规律.
(4)设中间数为a,则5个数之和为(a-12)+(a-2)+a+(a+2)+(a+12)=5a.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
