高中物理人教版选修3-3课后练习题 8.2气体的等容变化和等压变化 Word版含解析
文档属性
| 名称 | 高中物理人教版选修3-3课后练习题 8.2气体的等容变化和等压变化 Word版含解析 | 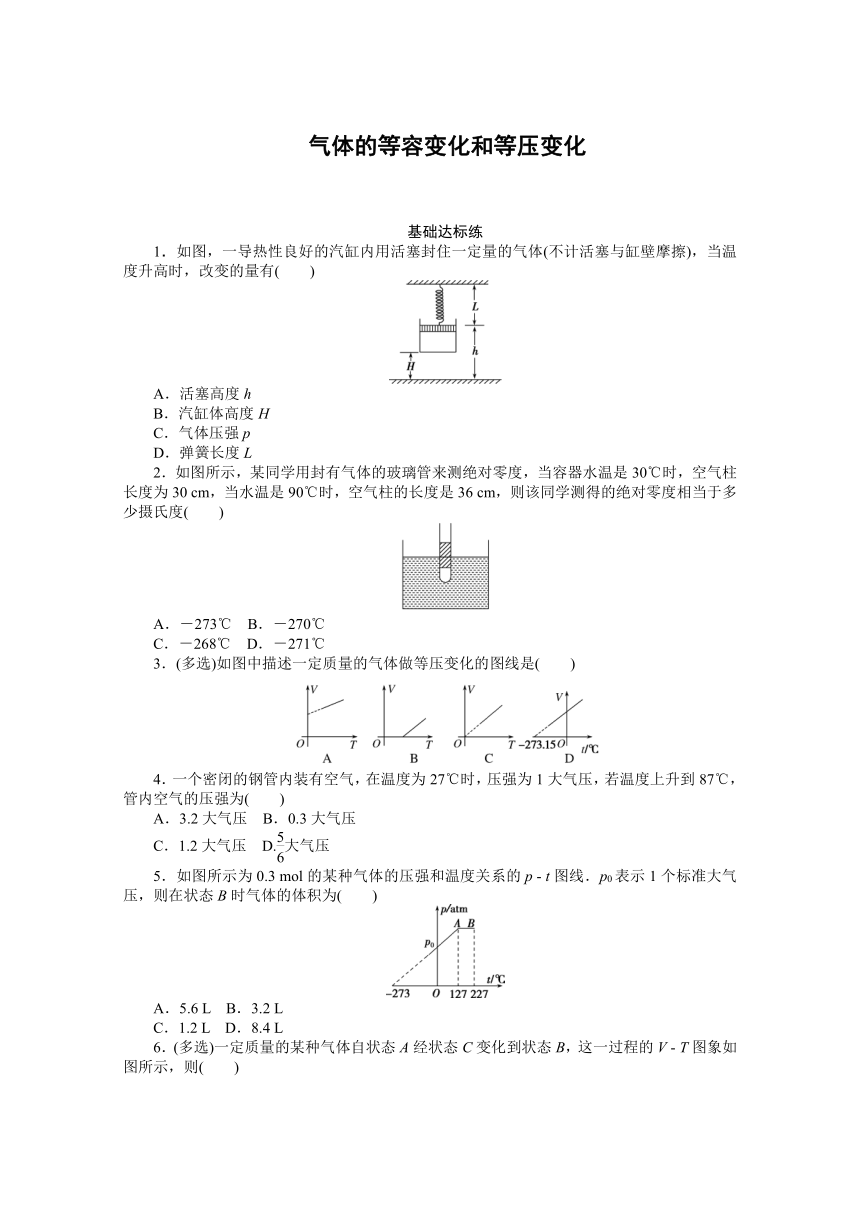 | |
| 格式 | doc | ||
| 文件大小 | 210.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-10 15:42:12 | ||
图片预览



文档简介
气体的等容变化和等压变化
基础达标练
1.如图,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),当温度升高时,改变的量有( )
A.活塞高度h
B.汽缸体高度H
C.气体压强p
D.弹簧长度L
2.如图所示,某同学用封有气体的玻璃管来测绝对零度,当容器水温是30℃时,空气柱长度为30 cm,当水温是90℃时,空气柱的长度是36 cm,则该同学测得的绝对零度相当于多少摄氏度( )
A.-273℃ B.-270℃
C.-268℃ D.-271℃
3.(多选)如图中描述一定质量的气体做等压变化的图线是( )
4.一个密闭的钢管内装有空气,在温度为27℃时,压强为1大气压,若温度上升到87℃,管内空气的压强为( )
A.3.2大气压 B.0.3大气压
C.1.2大气压 D.大气压
5.如图所示为0.3 mol的某种气体的压强和温度关系的p ? t图线.p0表示1个标准大气压,则在状态B时气体的体积为( )
A.5.6 L B.3.2 L
C.1.2 L D.8.4 L
6.(多选)一定质量的某种气体自状态A经状态C变化到状态B,这一过程的V ? T图象如图所示,则( )
A.在过程A→C中,气体的压强不断变小
B.在过程C→B中,气体的压强不断变大
C.在状态A时,气体的压强最小
D.在状态B时,气体的压强最大
7.(多选)如图所示,甲、乙为一定质量的某种气体的等容或等压变化图象,关于这两个图象的正确说法是( )
A.甲是等压线,乙是等容线
B.乙图中p ? t图线与t轴交点对应的温度是-273.15 ℃,而甲图中V ? t图线与t轴的交点不一定是-273.15 ℃
C.由乙图可知,一定质量的气体,在任何情况下都是p与t成直线关系
D.乙图表明温度每升高1 ℃,压强增加相同,但甲图表明随温度的升高压强不变
8.有一上端开口、竖直放置的玻璃管,管中有一段15 cm长的水银柱将一些空气封闭在管中,如图所示,此时气体的温度为27℃.当温度升高到30℃时,为了使气体体积不变,需要再注入多少水银?(设大气压强为p0=75 cmHg且不变,水银密度ρ=13.6 g/cm3)
9.如图所示,透热的汽缸内封有一定质量的理想气体,缸体质量M=200 kg,活塞质量m=10 kg,活塞面积S=100 cm2,活塞与汽缸壁无摩擦且不漏气,此时,缸内气体的温度为27 ℃,活塞位于汽缸正中,整个装置都静止,已知大气压强为p0=1.0×105 Pa,重力加速度为g=10 m/s2,T=t+273 K,求:
(1)缸内气体的压强p1;
(2)缸内气体的温度升高到多少摄氏度时,活塞恰好会静止在汽缸缸口AB处?
能力提升练
10.一定质量的理想气体在等压变化中体积增大了,若气体原来温度为27 ℃,则温度的变化是( )
A.升高了450 K B.升高了150 ℃
C.升高了40.5 ℃ D.升高了450 ℃
11.如图所示是一定质量的气体从状态A经过状态B到状态C,再到状态A的p ? T图象,由图可知( )
A.VA=VB B.VB>VC
C.VB=VC D.VA>VC
12.如图所示,带有刻度的注射器竖直固定在铁架台上,其下部放入盛水的烧杯中.注射器活塞的横截面积S=5×10-5 m2,活塞及框架的总质量m0=5×10-2 kg,大气压强p0=1.0×105 Pa.当水温为t0=13 ℃时,注射器内气体的体积为5.5 mL.求:(g取10 m/s2)
(1)向烧杯中加入热水,稳定后测得t1=65 ℃时,气体的体积为多大?
(2)保持水温t1=65 ℃不变,为使气体的体积恢复到5.5 mL,则要在框架上挂质量多大的钩码?
13.汽车行驶时轮胎的胎压太高容易造成爆胎事故,太低会造成耗油上升.已知某型号轮胎能在-40 ℃~90 ℃正常工作,为使轮胎在此温度范围内工作时的最高胎压不超过3.5 atm,最低胎压不低于1.6 atm,那么t=20 ℃时给该轮胎充气,充气后的胎压在什么范围内比较合适?(设轮胎容积不变)
分层训练(七) 气体的等容变化和等压变化
1.解析:气体做等压变化,温度升高时,体积变大,所以汽缸体高度H减小.
答案:B
2.解析:设绝对零度相当于T0
则初态:T1=-T0+30℃,V1=30S
末态:T2=-T0+90℃,V2=36S
由盖—吕萨克定律=
代入数据解得T0=-270℃.故选B.
答案:B
3.解析:等压线的延长线与横轴的交点为热力学温度的零度,故C、D正确.
答案:CD
4.解析:由查理定律得=,故p2=1.2个大气压,C正确.
答案:C
5.解析:此气体在0 ℃时,压强为标准大气压,所以它的体积应为22.4×0.3 L=6.72 L,根据图线所示,从p0到A状态,气体是等容变化,A状态的体积为6.72 L,温度为127 K+273 K=400 K,从A状态到B状态为等压变化,B状态的温度为227 K+273 K=500 K,根据盖—吕萨克定律=得,VB== L=8.4 L.
答案:D
6.解析:A→C过程中,气体的体积不变,发生等容变化,由=C可知,温度升高,压强增大,故A错误;在C→B过程中,发生等温变化,由pV=C可知,体积减小,压强增大,故B正确;综上所述,在A→C→B过程中,气体的压强始终增大,所以气体在状态B时的压强最大,在状态A时的压强最小,故C、D正确.
答案:BCD
7.解析:由查理定律p=CT=C(t+273.15)及盖—吕萨克定律V=CT=C(t+273.15)可知,甲图是等压线,乙图是等容线,故A正确;由“外推法”可知两种图线的反向延长线与t轴的交点温度为-273.15℃,即热力学温度的0 K,故B错;查理定律及盖—吕萨克定律是气体的实验定律,都是在温度不太低、压强不太大的条件下得出的,当压强很大,温度很低时,这些定律就不成立了,故C错;由于图线是直线,故D正确.
答案:AD
8.解析:设再注入的水银柱长为x,以封闭在管中的气体为研究对象,气体做等容变化.
初态:p1=p0+15 cmHg=90 cmHg,T1=(273+27) K=300 K;末态:p2=(90+x) cmHg,T2=(273+30) K=303 K.
由查理定律=得=,解得x=0.9 cm.则注入水银柱的长度为0.9 cm.
答案:注入水银柱的长度为0.9 cm
9.解析:(1)以汽缸为研究对象(不包括活塞),列汽缸受力平衡方程:p1S=Mg+p0S,
解得:p1=3×105 Pa.
(2)当活塞恰好静止在汽缸缸口AB处时,缸内气体温度为T2,压强为p2,
此时仍有p2S=Mg+p0S,
由题意知缸内气体为等压变化,对这一过程研究缸内气体,
由盖—吕萨克定律得:=
所以T2=2T1=600 K,故t2=(600-273)℃=327 ℃.
答案:(1)3×105 Pa (2)327 ℃
10.解析:根据盖—吕萨克定律,可得=,ΔT=ΔV= K×V=150 K.升高了150 K和升高了150℃是等效的,故B正确.
答案:B
11.解析:A沿直线到B是等容过程,因此VA=VB,故A项正确;连接OC可知,直线OC的斜率比直线OB的斜率小,因此VB<VC,VA<VC,故B、C、D均错误.
答案:A
12.解析:(1)由盖—吕萨克定律=,得V1=6.5 mL
(2)由玻意耳定律
ρ0+V1=p0+V0,
解得m=0.1 kg
答案:(1)6.5 mL (2)0.1 kg
13.解析:由于轮胎容积不变,轮胎内气体做等容变化.
设在T0=293 K充气后的最小胎压为pmin最大胎压为pmax.依题意知,当T1=233 K时胎压为p1=1.6 atm.
根据查理定律=,即=.
解得:pmin=2.01 atm.
当T2=363 K时胎压为p2=3.5 atm.根据查理定律=,即=.
解得:pmax=2.83 atm.
答案:2.01 atm~2.83 atm
基础达标练
1.如图,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),当温度升高时,改变的量有( )
A.活塞高度h
B.汽缸体高度H
C.气体压强p
D.弹簧长度L
2.如图所示,某同学用封有气体的玻璃管来测绝对零度,当容器水温是30℃时,空气柱长度为30 cm,当水温是90℃时,空气柱的长度是36 cm,则该同学测得的绝对零度相当于多少摄氏度( )
A.-273℃ B.-270℃
C.-268℃ D.-271℃
3.(多选)如图中描述一定质量的气体做等压变化的图线是( )
4.一个密闭的钢管内装有空气,在温度为27℃时,压强为1大气压,若温度上升到87℃,管内空气的压强为( )
A.3.2大气压 B.0.3大气压
C.1.2大气压 D.大气压
5.如图所示为0.3 mol的某种气体的压强和温度关系的p ? t图线.p0表示1个标准大气压,则在状态B时气体的体积为( )
A.5.6 L B.3.2 L
C.1.2 L D.8.4 L
6.(多选)一定质量的某种气体自状态A经状态C变化到状态B,这一过程的V ? T图象如图所示,则( )
A.在过程A→C中,气体的压强不断变小
B.在过程C→B中,气体的压强不断变大
C.在状态A时,气体的压强最小
D.在状态B时,气体的压强最大
7.(多选)如图所示,甲、乙为一定质量的某种气体的等容或等压变化图象,关于这两个图象的正确说法是( )
A.甲是等压线,乙是等容线
B.乙图中p ? t图线与t轴交点对应的温度是-273.15 ℃,而甲图中V ? t图线与t轴的交点不一定是-273.15 ℃
C.由乙图可知,一定质量的气体,在任何情况下都是p与t成直线关系
D.乙图表明温度每升高1 ℃,压强增加相同,但甲图表明随温度的升高压强不变
8.有一上端开口、竖直放置的玻璃管,管中有一段15 cm长的水银柱将一些空气封闭在管中,如图所示,此时气体的温度为27℃.当温度升高到30℃时,为了使气体体积不变,需要再注入多少水银?(设大气压强为p0=75 cmHg且不变,水银密度ρ=13.6 g/cm3)
9.如图所示,透热的汽缸内封有一定质量的理想气体,缸体质量M=200 kg,活塞质量m=10 kg,活塞面积S=100 cm2,活塞与汽缸壁无摩擦且不漏气,此时,缸内气体的温度为27 ℃,活塞位于汽缸正中,整个装置都静止,已知大气压强为p0=1.0×105 Pa,重力加速度为g=10 m/s2,T=t+273 K,求:
(1)缸内气体的压强p1;
(2)缸内气体的温度升高到多少摄氏度时,活塞恰好会静止在汽缸缸口AB处?
能力提升练
10.一定质量的理想气体在等压变化中体积增大了,若气体原来温度为27 ℃,则温度的变化是( )
A.升高了450 K B.升高了150 ℃
C.升高了40.5 ℃ D.升高了450 ℃
11.如图所示是一定质量的气体从状态A经过状态B到状态C,再到状态A的p ? T图象,由图可知( )
A.VA=VB B.VB>VC
C.VB=VC D.VA>VC
12.如图所示,带有刻度的注射器竖直固定在铁架台上,其下部放入盛水的烧杯中.注射器活塞的横截面积S=5×10-5 m2,活塞及框架的总质量m0=5×10-2 kg,大气压强p0=1.0×105 Pa.当水温为t0=13 ℃时,注射器内气体的体积为5.5 mL.求:(g取10 m/s2)
(1)向烧杯中加入热水,稳定后测得t1=65 ℃时,气体的体积为多大?
(2)保持水温t1=65 ℃不变,为使气体的体积恢复到5.5 mL,则要在框架上挂质量多大的钩码?
13.汽车行驶时轮胎的胎压太高容易造成爆胎事故,太低会造成耗油上升.已知某型号轮胎能在-40 ℃~90 ℃正常工作,为使轮胎在此温度范围内工作时的最高胎压不超过3.5 atm,最低胎压不低于1.6 atm,那么t=20 ℃时给该轮胎充气,充气后的胎压在什么范围内比较合适?(设轮胎容积不变)
分层训练(七) 气体的等容变化和等压变化
1.解析:气体做等压变化,温度升高时,体积变大,所以汽缸体高度H减小.
答案:B
2.解析:设绝对零度相当于T0
则初态:T1=-T0+30℃,V1=30S
末态:T2=-T0+90℃,V2=36S
由盖—吕萨克定律=
代入数据解得T0=-270℃.故选B.
答案:B
3.解析:等压线的延长线与横轴的交点为热力学温度的零度,故C、D正确.
答案:CD
4.解析:由查理定律得=,故p2=1.2个大气压,C正确.
答案:C
5.解析:此气体在0 ℃时,压强为标准大气压,所以它的体积应为22.4×0.3 L=6.72 L,根据图线所示,从p0到A状态,气体是等容变化,A状态的体积为6.72 L,温度为127 K+273 K=400 K,从A状态到B状态为等压变化,B状态的温度为227 K+273 K=500 K,根据盖—吕萨克定律=得,VB== L=8.4 L.
答案:D
6.解析:A→C过程中,气体的体积不变,发生等容变化,由=C可知,温度升高,压强增大,故A错误;在C→B过程中,发生等温变化,由pV=C可知,体积减小,压强增大,故B正确;综上所述,在A→C→B过程中,气体的压强始终增大,所以气体在状态B时的压强最大,在状态A时的压强最小,故C、D正确.
答案:BCD
7.解析:由查理定律p=CT=C(t+273.15)及盖—吕萨克定律V=CT=C(t+273.15)可知,甲图是等压线,乙图是等容线,故A正确;由“外推法”可知两种图线的反向延长线与t轴的交点温度为-273.15℃,即热力学温度的0 K,故B错;查理定律及盖—吕萨克定律是气体的实验定律,都是在温度不太低、压强不太大的条件下得出的,当压强很大,温度很低时,这些定律就不成立了,故C错;由于图线是直线,故D正确.
答案:AD
8.解析:设再注入的水银柱长为x,以封闭在管中的气体为研究对象,气体做等容变化.
初态:p1=p0+15 cmHg=90 cmHg,T1=(273+27) K=300 K;末态:p2=(90+x) cmHg,T2=(273+30) K=303 K.
由查理定律=得=,解得x=0.9 cm.则注入水银柱的长度为0.9 cm.
答案:注入水银柱的长度为0.9 cm
9.解析:(1)以汽缸为研究对象(不包括活塞),列汽缸受力平衡方程:p1S=Mg+p0S,
解得:p1=3×105 Pa.
(2)当活塞恰好静止在汽缸缸口AB处时,缸内气体温度为T2,压强为p2,
此时仍有p2S=Mg+p0S,
由题意知缸内气体为等压变化,对这一过程研究缸内气体,
由盖—吕萨克定律得:=
所以T2=2T1=600 K,故t2=(600-273)℃=327 ℃.
答案:(1)3×105 Pa (2)327 ℃
10.解析:根据盖—吕萨克定律,可得=,ΔT=ΔV= K×V=150 K.升高了150 K和升高了150℃是等效的,故B正确.
答案:B
11.解析:A沿直线到B是等容过程,因此VA=VB,故A项正确;连接OC可知,直线OC的斜率比直线OB的斜率小,因此VB<VC,VA<VC,故B、C、D均错误.
答案:A
12.解析:(1)由盖—吕萨克定律=,得V1=6.5 mL
(2)由玻意耳定律
ρ0+V1=p0+V0,
解得m=0.1 kg
答案:(1)6.5 mL (2)0.1 kg
13.解析:由于轮胎容积不变,轮胎内气体做等容变化.
设在T0=293 K充气后的最小胎压为pmin最大胎压为pmax.依题意知,当T1=233 K时胎压为p1=1.6 atm.
根据查理定律=,即=.
解得:pmin=2.01 atm.
当T2=363 K时胎压为p2=3.5 atm.根据查理定律=,即=.
解得:pmax=2.83 atm.
答案:2.01 atm~2.83 atm
