三角形中的边角关系

(共16张PPT)
生活中的三角形
生活中的三角形
生活中的三角形
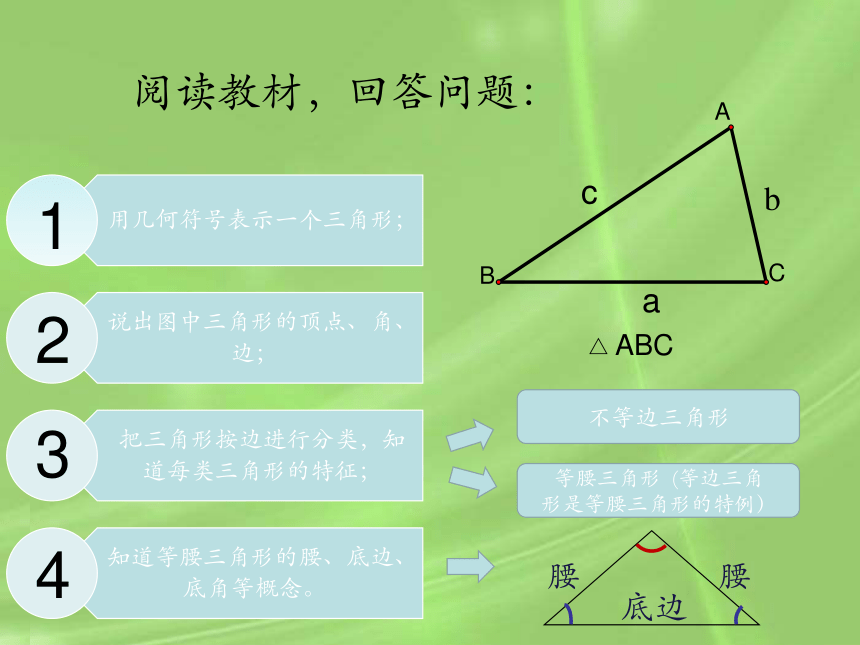
阅读教材，回答问题：
1
2
3
4
A
B
C
不等边三角形
等腰三角形 (等边三角
形是等腰三角形的特例）
腰
腰
底边
a
c
b
ABC
△
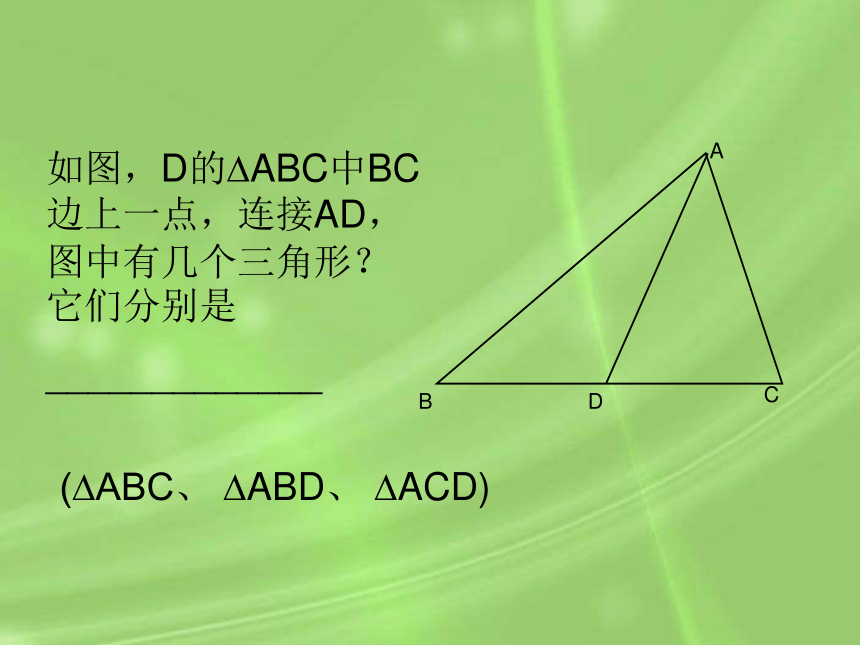
如图，D的 ABC中BC边上一点，连接AD，图中有几个三角形？它们分别是
_____________
A
B
D
C
( ABC、 ABD、 ACD)
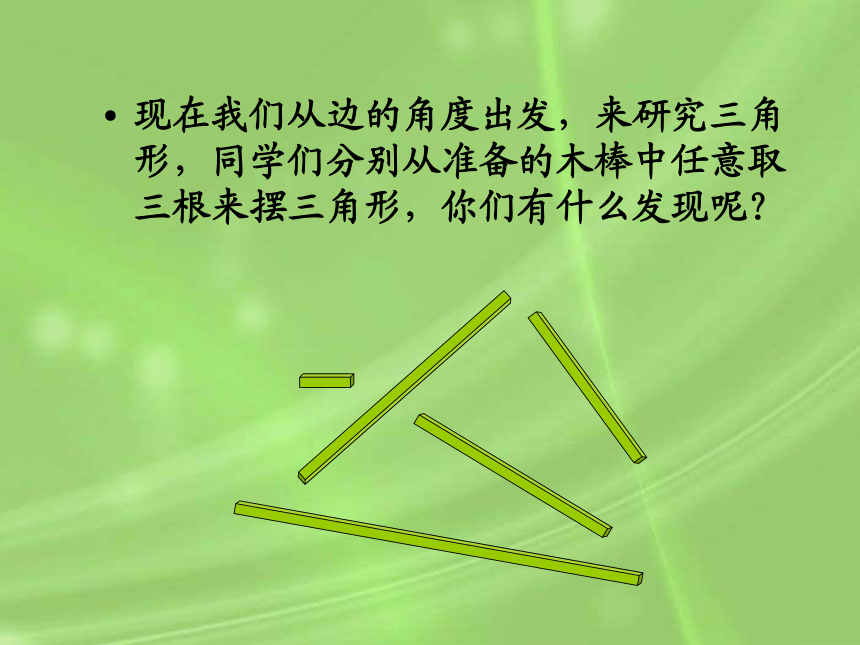
现在我们从边的角度出发，来研究三角形，同学们分别从准备的木棒中任意取三根来摆三角形，你们有什么发现呢？
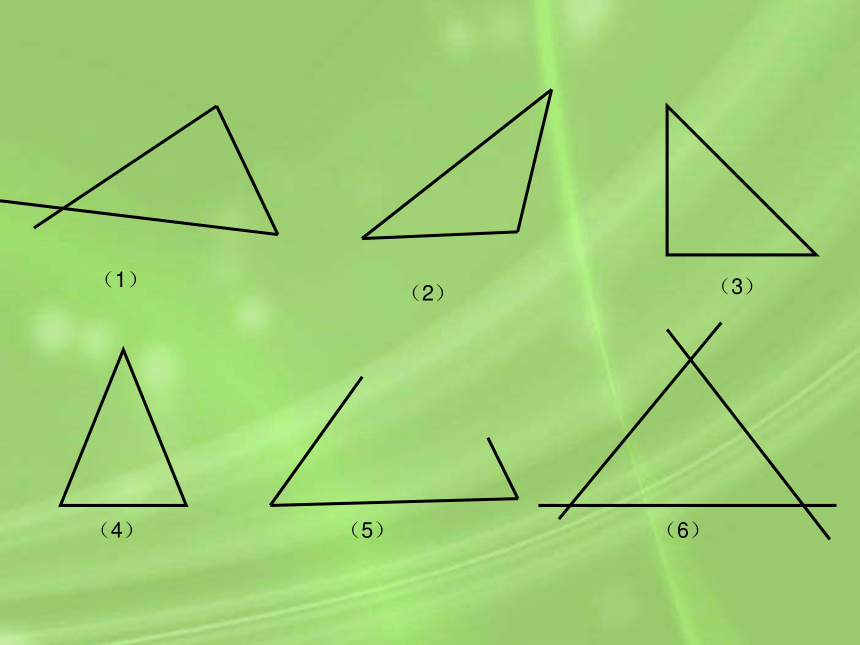
（1）
（6）
（5）
（4）
（3）
（2）
三角形任意两边之和大于第三边。
（三角形任意两边之差小于第三边。）
判断：用下列长度的三条线段能否组成一个三角形？
（1）1cm、2cm、3cm;
（2）2cm、3cm、4cm;
（3）4cm、5cm、6cm;
（4）5cm、6cm、10cm.
（1）不能；（2）（3）（4）能
例：等腰三角形中周长为18cm
（1）如果腰长是底边长的2倍，求各边的长；
（2）如果一边长为4cm，求另两边的长。
（1）设等腰三角形的底边长为xcm，
则腰长为2xcm，根据题意，得
x+2x+2x=18
解方程，得
x=3.6
解：
（2）若底边长为4cm，设腰长为xcm,则有
2x+4=18
解方程，得
x=7
若一条腰长为4cm，设底边长为xcm，则有
2×4+x=18
x=10
解方程，得
因为4+4<10，所以4cm为一腰不能构成三角形
所以，三角形的另两边长都是7cm
一根木棒长为7，另一根木棒长为2，那么用长度为9的木棒
能和它们拼成三角形吗？长度为11的木棒呢？若能拼成，则
第三条边应在什么范围呢？
小结：设x为三角形第三条边，
则 两边之差巩固新知
已知三角形三条边都是整数，其中两边长度分别
为7cm和2cm，且第三边为奇数，求此三角形周长。
提高训练
练习：
1、以长4 cm 的线段为底构造一个等腰三角形，这个三角形的腰长有什么限制？
2、若以整数a、b、c为三边长的三角形，满足等式（2a-b)2+|4-b| = 0,则这样的三角形的周长最小值是 __________ ，最大值是___________ 。
腰长大于2cm
9
11
请同学们回顾本节课所学的内容，你有哪些收获？
（1）三角形的概念及表示
（2）三角形三边的关系
（3）三角形三边关系的应用
小 结
习题14.1的第1题。
作 业