14.1 勾股定理(第1课时 直角三角形三边的关系)
文档属性
| 名称 | 14.1 勾股定理(第1课时 直角三角形三边的关系) |

|
|
| 格式 | rar | ||
| 文件大小 | 814.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-26 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
华东师大版八年级(上册)
第14章 勾股定理
14.1 勾股定理(第1课时)
直角三角形三边的关系
A
B
C
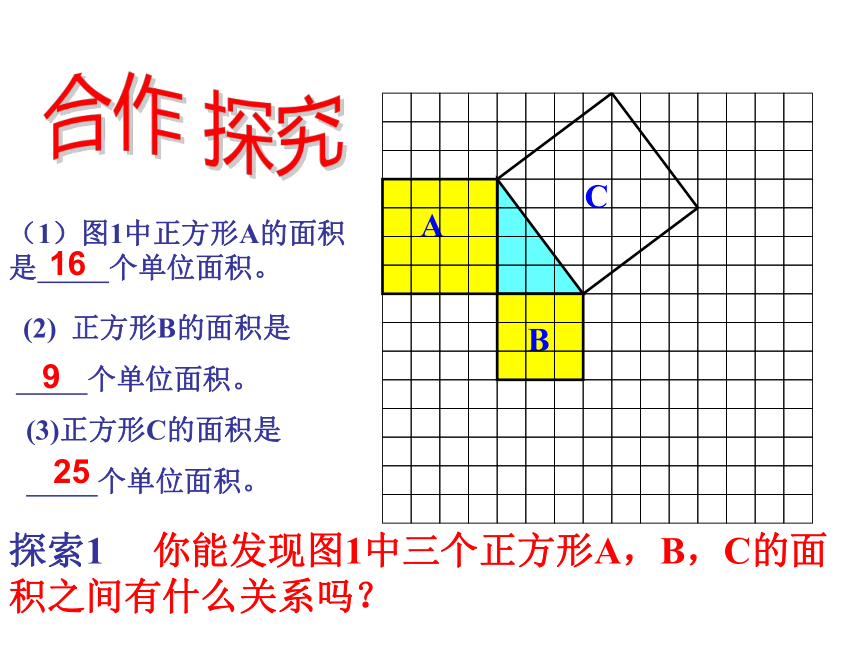
(1)图1中正方形A的面积是 个单位面积。
(2) 正方形B的面积是
个单位面积。
(3)正方形C的面积是
个单位面积。
16
9
25
探索1 你能发现图1中三个正方形A,B,C的面积之间有什么关系吗?
A
B
C
结论1 SA+SB=SC
探索2 你能用直角三角形的边长表示图中正方形的面积吗?
探索3 你能发现图中直角三角形三边长度之间存在什么关系吗?
a
c
b
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积。
勾股定理
如果直角三角形两直角边分别为a、b, 斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
在西方又称 毕达哥拉斯定理
勾
股
弦
b
a
c
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
已知一个三角形斜边长17厘米、一条直角边长15厘米的
直角三角形,求这个三角形的面积.
解: 如 图, 设另一条直角边长是 x 厘米.由勾股定理得:
152 + x2 = 172
而 x2 = 172 - 152
= 289 – 225 = 64
所以 :x=8
直角三角形的面积是:
(平方厘米)
x
15
17
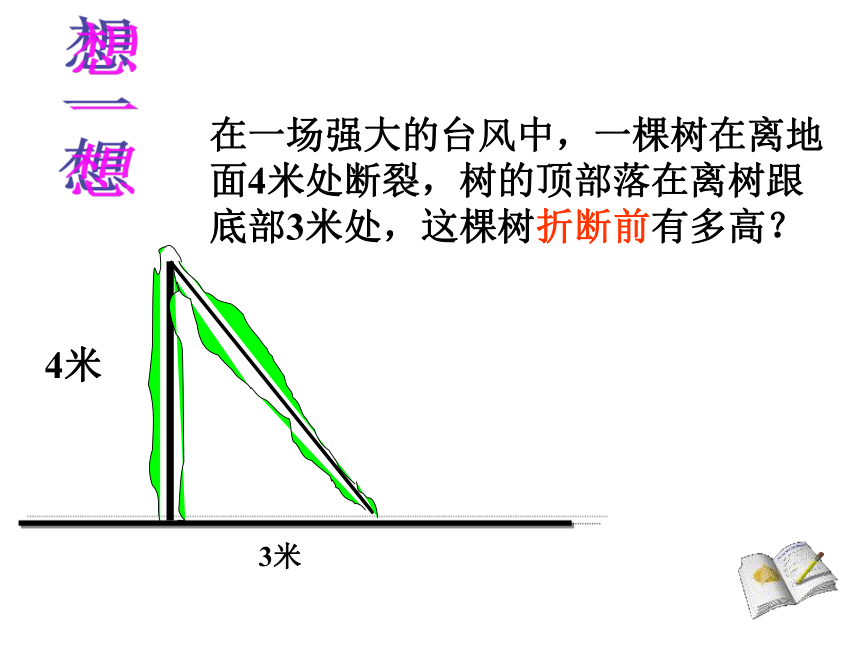
在一场强大的台风中,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
1、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.
=625
225
400
A
225
81
B
=144
想一想
2. 小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
我们通常所说的29英寸或74厘米的电视机,是指其荧屏对角线的长度
∴售货员没搞错
∵
荧屏对角线大约为74厘米
46
58
A
B
C
D
7cm
如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。
49
议一议
美丽的勾股树(一)
美丽的勾股树(二)
中国最早的一部数学著作《周髀(bì) 算经》中记录着在公元前1100年左右的西周时期数学家商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。” 后来人们就简单地把这个事实说成“勾三股四弦五”。这就是著名的勾股定理。
在稍后一点的《九章算术》( 约在 公元50至100年间)一书中,勾股定理得到了更加规范的一般性表达。书中的《勾股章》说:“把勾和股分别自乘,然后把它们的积加起来,再进行开方,便可以得到弦。”
我国最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。
毕达哥拉斯
在国外,相传勾股定理是公元前550年古希腊数学家兼哲学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。但毕达哥拉斯对勾股定理的证明方法已经失传。且他发现的时间比我国要迟得多。
小结
1、利用数格子的方法,探索了以直角三角形三边为边长的正方形面积的关系(即两个小正方形的面积之和等于大正方形的面积)
2、探索了直角三角形的三边关系, 得到勾股定理:
即直角三角形两直角边的平方和等于斜边的平方平
A的面积+B的面积=C的面积
a2+b2=c2
C
c
b
a
A
B
y=0
总结反思布置作业
华东师大版八年级(上册)
第14章 勾股定理
14.1 勾股定理(第1课时)
直角三角形三边的关系
A
B
C
(1)图1中正方形A的面积是 个单位面积。
(2) 正方形B的面积是
个单位面积。
(3)正方形C的面积是
个单位面积。
16
9
25
探索1 你能发现图1中三个正方形A,B,C的面积之间有什么关系吗?
A
B
C
结论1 SA+SB=SC
探索2 你能用直角三角形的边长表示图中正方形的面积吗?
探索3 你能发现图中直角三角形三边长度之间存在什么关系吗?
a
c
b
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积。
勾股定理
如果直角三角形两直角边分别为a、b, 斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
在西方又称 毕达哥拉斯定理
勾
股
弦
b
a
c
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
已知一个三角形斜边长17厘米、一条直角边长15厘米的
直角三角形,求这个三角形的面积.
解: 如 图, 设另一条直角边长是 x 厘米.由勾股定理得:
152 + x2 = 172
而 x2 = 172 - 152
= 289 – 225 = 64
所以 :x=8
直角三角形的面积是:
(平方厘米)
x
15
17
在一场强大的台风中,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
1、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.
=625
225
400
A
225
81
B
=144
想一想
2. 小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
我们通常所说的29英寸或74厘米的电视机,是指其荧屏对角线的长度
∴售货员没搞错
∵
荧屏对角线大约为74厘米
46
58
A
B
C
D
7cm
如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。
49
议一议
美丽的勾股树(一)
美丽的勾股树(二)
中国最早的一部数学著作《周髀(bì) 算经》中记录着在公元前1100年左右的西周时期数学家商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。” 后来人们就简单地把这个事实说成“勾三股四弦五”。这就是著名的勾股定理。
在稍后一点的《九章算术》( 约在 公元50至100年间)一书中,勾股定理得到了更加规范的一般性表达。书中的《勾股章》说:“把勾和股分别自乘,然后把它们的积加起来,再进行开方,便可以得到弦。”
我国最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。
毕达哥拉斯
在国外,相传勾股定理是公元前550年古希腊数学家兼哲学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。但毕达哥拉斯对勾股定理的证明方法已经失传。且他发现的时间比我国要迟得多。
小结
1、利用数格子的方法,探索了以直角三角形三边为边长的正方形面积的关系(即两个小正方形的面积之和等于大正方形的面积)
2、探索了直角三角形的三边关系, 得到勾股定理:
即直角三角形两直角边的平方和等于斜边的平方平
A的面积+B的面积=C的面积
a2+b2=c2
C
c
b
a
A
B
y=0
总结反思布置作业
