14.1 勾股定理(第2课时 直角三角形三边的关系)
文档属性
| 名称 | 14.1 勾股定理(第2课时 直角三角形三边的关系) |

|
|
| 格式 | rar | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-26 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
华东师大版八年级(上册)
第14章 勾股定理
14.1 勾股定理(第2课时)
直角三角形三边的关系
2002年国际数学家大会会标
赵爽
弦图
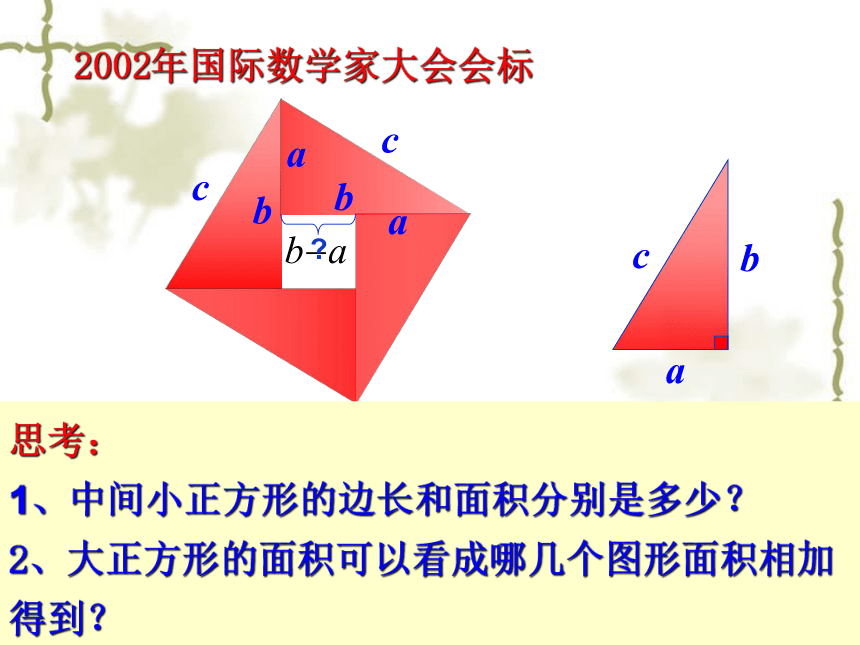
2002年国际数学家大会会标
思考:
1、中间小正方形的边长和面积分别是多少?
2、大正方形的面积可以看成哪几个图形面积相加得到?
3、根据上题可以写出怎样一个关系式?
a
b
c
b
c
a
c
b
a
b
c
a
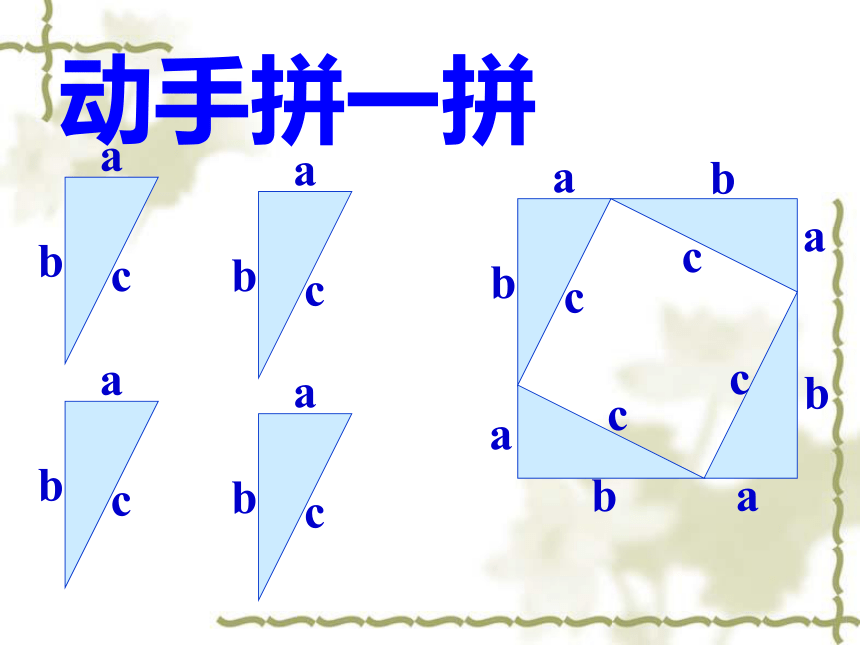
动手拼一拼
b
c
a
b
c
a
b
c
a
b
c
a
b
a
c
a
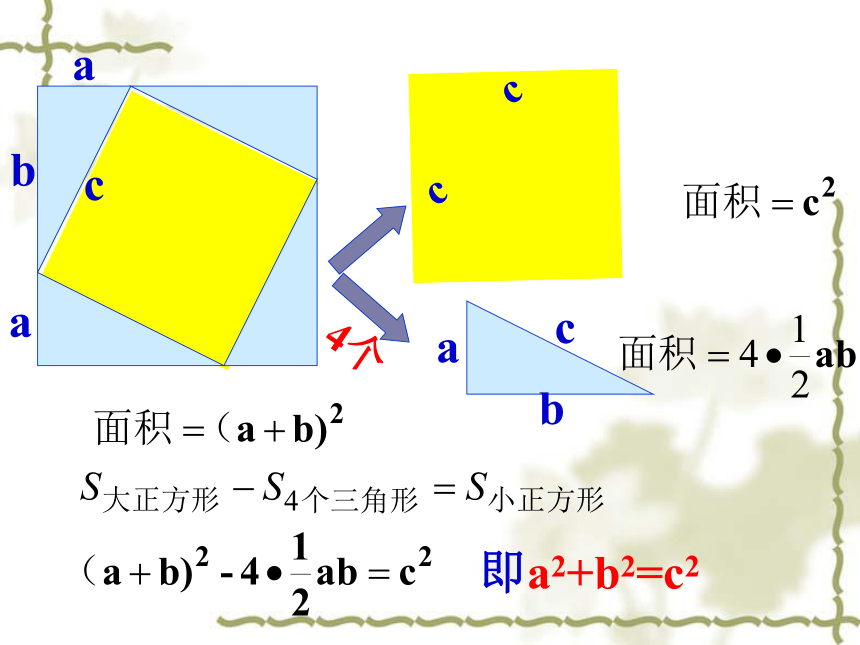
即a2+b2=c2
c
c
a
b
c
4个
伽菲尔德
1881 年成为美国第 20 任总统
1876 年提出有关证明,
证法称为“总统”证法
例1 我方侦察员小王在距离东西方向公路400米处侦察,发现一辆汽车在公路上行驶,他赶紧拿出红外线测距仪,测得汽车与他相距400米,10秒后,汽车与他相距500米,你能帮小王计算敌方汽车的速度吗?
C
A
B
公路
400米
500米
∟
例2 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000米处,过了20秒,飞机距离这个男孩5000米,飞机每小时飞行多少千米?
4000
5000
5000
4000
C
B
A
A
D
B
C
3
4
1.已知∠ACB=Rt∠,
CD⊥AB,AC=3,BC=4.
求CD的长.
C
80
60
25
24
B
A
2. 如图所示是某机械零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)
(1)直角三角形的两直角边为3和4,则斜边为___
(3)直角三角形的两直角边为6和8,则斜边为___
(2)直角三角形的两直角边为5和12,则斜边为___
(5)直角三角形的两条边为3和4,则斜边上的高是 。
(4)直角三角形的两条边为3和4,则这个直角三角形的周长为 。
12
或
5
10
13
补充练习:
1、放学以后,小红和小颖从学校分手,分别沿着东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米; B、800米; C、1000米; D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米; B、 8厘米; C、 80/13厘米;D、 60/13厘米;
C
D
3、等腰三角形底边上的高为8,周长为32,求这个三角形的面积
8
X
16-X
D
A
B
C
解:设这个三角形为ABC,高为AD,设BD为X,则AB为(16-X),
由勾股定理得:
X2+82=(16-X)2
即X2+64=256-32X+X2
∴ X=6
∴ S ABC=BC AD/2=2 6 8/2=48
你能想到不同的证明勾股定理的方法吗
华东师大版八年级(上册)
第14章 勾股定理
14.1 勾股定理(第2课时)
直角三角形三边的关系
2002年国际数学家大会会标
赵爽
弦图
2002年国际数学家大会会标
思考:
1、中间小正方形的边长和面积分别是多少?
2、大正方形的面积可以看成哪几个图形面积相加得到?
3、根据上题可以写出怎样一个关系式?
a
b
c
b
c
a
c
b
a
b
c
a
动手拼一拼
b
c
a
b
c
a
b
c
a
b
c
a
b
a
c
a
即a2+b2=c2
c
c
a
b
c
4个
伽菲尔德
1881 年成为美国第 20 任总统
1876 年提出有关证明,
证法称为“总统”证法
例1 我方侦察员小王在距离东西方向公路400米处侦察,发现一辆汽车在公路上行驶,他赶紧拿出红外线测距仪,测得汽车与他相距400米,10秒后,汽车与他相距500米,你能帮小王计算敌方汽车的速度吗?
C
A
B
公路
400米
500米
∟
例2 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000米处,过了20秒,飞机距离这个男孩5000米,飞机每小时飞行多少千米?
4000
5000
5000
4000
C
B
A
A
D
B
C
3
4
1.已知∠ACB=Rt∠,
CD⊥AB,AC=3,BC=4.
求CD的长.
C
80
60
25
24
B
A
2. 如图所示是某机械零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)
(1)直角三角形的两直角边为3和4,则斜边为___
(3)直角三角形的两直角边为6和8,则斜边为___
(2)直角三角形的两直角边为5和12,则斜边为___
(5)直角三角形的两条边为3和4,则斜边上的高是 。
(4)直角三角形的两条边为3和4,则这个直角三角形的周长为 。
12
或
5
10
13
补充练习:
1、放学以后,小红和小颖从学校分手,分别沿着东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米; B、800米; C、1000米; D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米; B、 8厘米; C、 80/13厘米;D、 60/13厘米;
C
D
3、等腰三角形底边上的高为8,周长为32,求这个三角形的面积
8
X
16-X
D
A
B
C
解:设这个三角形为ABC,高为AD,设BD为X,则AB为(16-X),
由勾股定理得:
X2+82=(16-X)2
即X2+64=256-32X+X2
∴ X=6
∴ S ABC=BC AD/2=2 6 8/2=48
你能想到不同的证明勾股定理的方法吗
