勾股定理

(共15张PPT)
渔洋中学数学组
折叠操作
　　折叠操作就是将图形的一部分沿着一条直线翻折180°，使它与另一部分图形在这条直线的同旁与其重叠或不重叠，其中“折”是过程，“叠”是结果.
折叠问题的实质是图形的轴对称变换，折叠更突出了轴对称问题的应用. 所以在解决有关的折叠问题时可以充分运用轴对称的思想和轴对称的性质.
根据轴对称的性质可以得到：
折叠重合部分一定全等，
折痕所在直线就是这两个全等形的对称轴；
互相重合两点（对称点）之间的连线必被折痕垂直平分；
对称两点与对称轴上任意一点连结所得的两条线段相等；
对称线段所在的直线与对称轴的夹角相等.
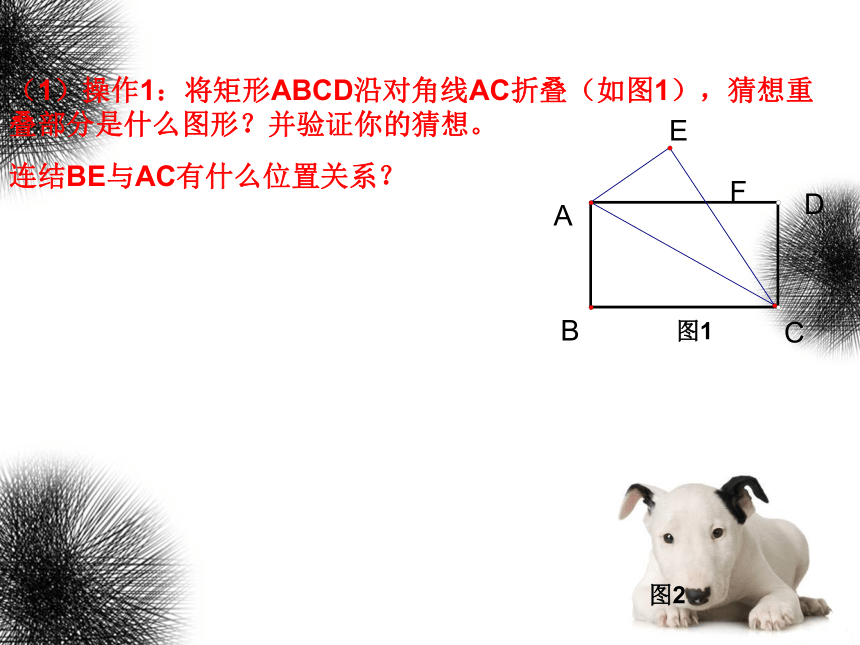
（1）操作1：将矩形ABCD沿对角线AC折叠（如图1），猜想重叠部分是什么图形？并验证你的猜想。
连结BE与AC有什么位置关系？
A
B
C
D
E
F
图1
图2
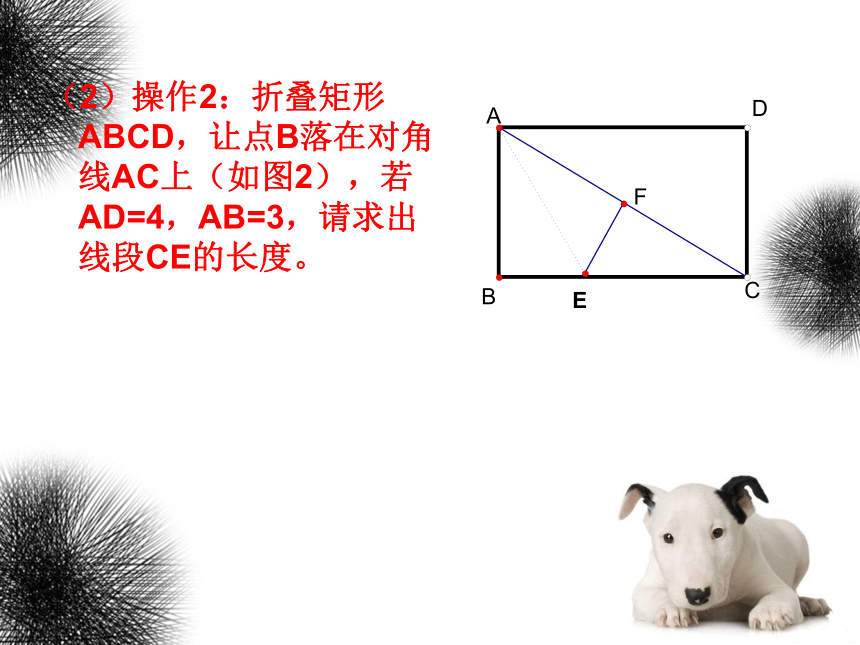
（2）操作2：折叠矩形ABCD，让点B落在对角线AC上（如图2），若AD=4，AB=3，请求出线段CE的长度。
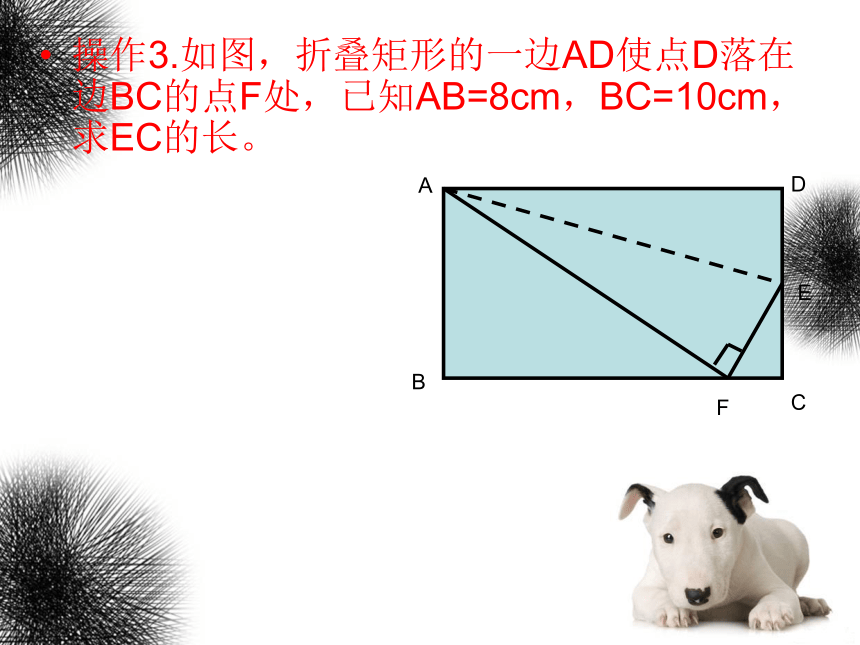
操作3.如图，折叠矩形的一边AD使点D落在边BC的点F处，已知AB=8cm，BC=10cm，求EC的长。
D
A
E
C
F
B
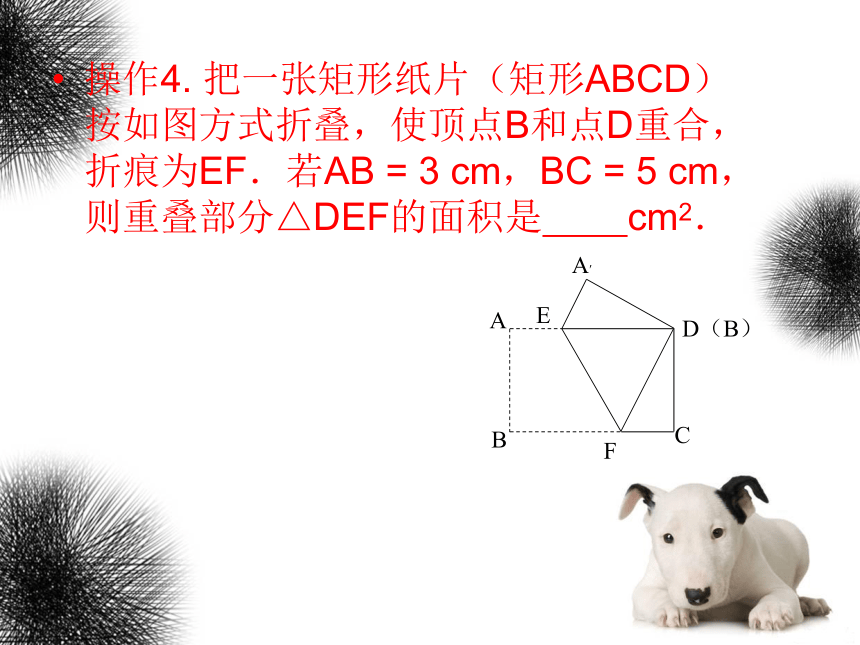
操作4. 把一张矩形纸片（矩形ABCD）按如图方式折叠，使顶点B和点D重合，折痕为EF．若AB = 3 cm，BC = 5 cm，则重叠部分△DEF的面积是 cm2．
A
B
C
F
E
A′
D（B）
分析：由于折叠易得AF=FC，再设BF=x，
从而FC=4-x，AF=x，在直角三角形ABF中
利用勾股定理就可以求出x。又能求出AC，
易求出OA，再在直角三角形AFO中求出OF，
从而求出EF。
如图，矩形ABCD中，AB=3，BC=4。若将该矩形折叠，使点C与点A重合，则折痕EF= 。
操作5.如图把矩形纸片ABCD沿EF折叠,
A
B
C
D
E
F
如图，将矩形纸片ABCD沿对角线AC折叠，使点B落在点B’ 处，AB ’交CD于点E.
A
B
C
D
B’
E
（1）△ACE是什么三角形？请说明理由.
（2）若AB=10，BC=8，则S△ACE= .
如图，将矩形纸片ABCD沿对角线AC折叠，使点B落在点B’ 处，AB ’交CD于点E.
（3）在第（2）题的条件下，设点F为BC边上的一个动点，若将纸片沿AF折叠后，点B恰好落在CD边上的点E处（如右图），则BF= .
A
B
C
D
F
E
1、把一张矩形纸片（矩形ABCD）按如图方式折叠，使顶点B和点D重合，折痕为EF．若AB = 3 cm，BC = 5 cm，则重叠部分△DEF的面积是 cm2．
A
B
C
F
E
A′
D（B）
2、如图，折叠矩形纸片ABCD，先折出折痕（对角线）BD，再折叠，使AD落在对角线BD上，得折痕DG，若AB = 2，BC = 1，则AG= .
G
A1
D
A
B
C
反思与小结
通过本节课的学习，你有哪些收获？
还有哪些困惑？
谢谢大家！请多指教！