3.1.2二分法与函数的零点 同步训练(含解析)
文档属性
| 名称 | 3.1.2二分法与函数的零点 同步训练(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2020-2021学年度高中数学必修一
二分法与函数的零点同步训练
第I卷(选择题)
一、单选题
1.设函数,
在用二分法求方程在内的近似解过程中得,则方程的解所在的区间是(
)
A.
B.
C.
D.
2.设,用二分法求方程在内近似解的过程中得,,,则方程的根落在区间
A.
B.
C.
D.不能确定
3.以下每个图象表示的函数都有零点,但不能用二分法求函数零点的是( )
A.
B.
C.
D.
4.函数的零点必落在区间(
)
A.
B.
C.
D.
5.函数的零点个数为(
)
A.
B.
C.
D.
6.下列函数的图象均与轴有交点,其中不宜用二分法求交点横坐标的是(
).
A.
B.
C.
D.
7.下列函数图像与x轴均有公共点,其中能用二分法求零点的是( )
A.
B.
C.
D.
8.函数f(x)=x+的零点个数为( )
A.0
B.1
C.2
D.3
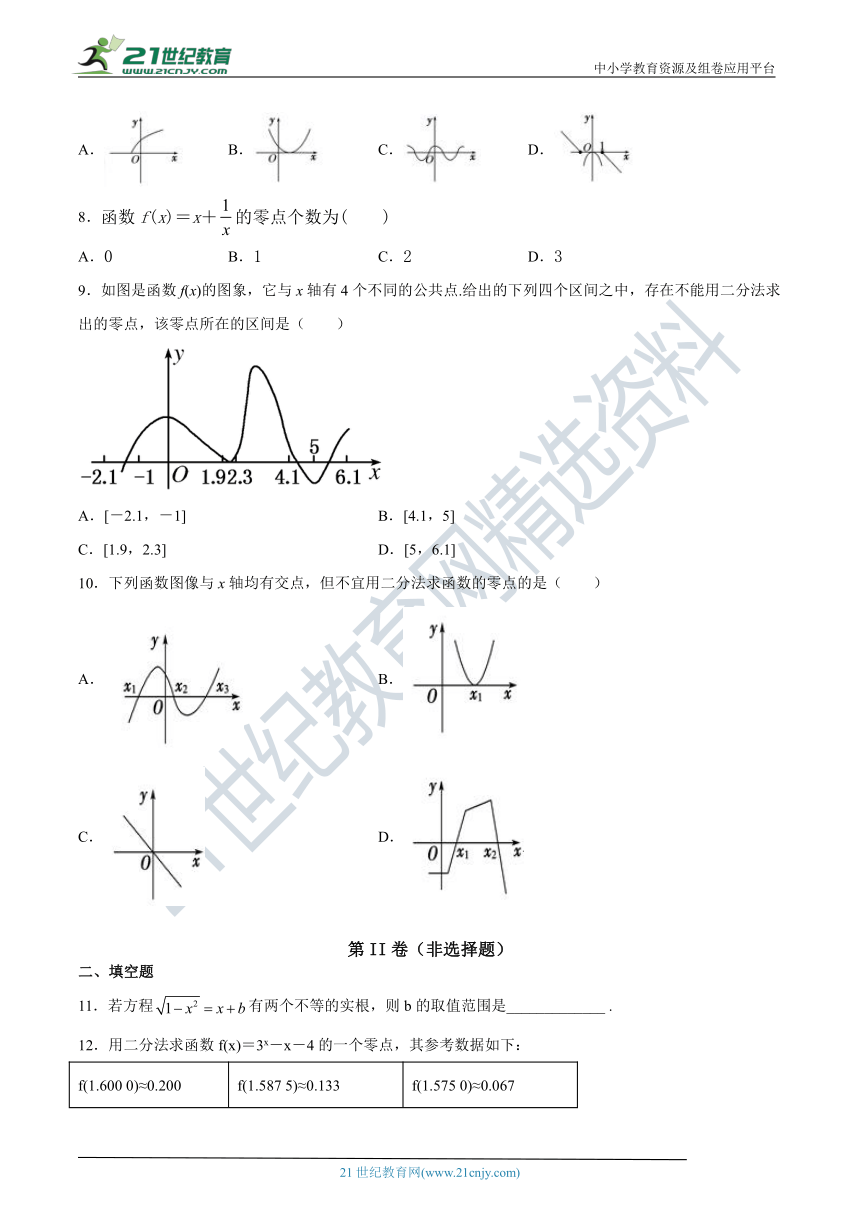
9.如图是函数f(x)的图象,它与x轴有4个不同的公共点.给出的下列四个区间之中,存在不能用二分法求出的零点,该零点所在的区间是(
)
A.[-2.1,-1]
B.[4.1,5]
C.[1.9,2.3]
D.[5,6.1]
10.下列函数图像与x轴均有交点,但不宜用二分法求函数的零点的是(
)
A.
B.
C.
D.
第II卷(非选择题)
二、填空题
11.若方程有两个不等的实根,则b的取值范围是_____________
.
12.用二分法求函数f(x)=3x-x-4的一个零点,其参考数据如下:
f(1.600
0)≈0.200
f(1.587
5)≈0.133
f(1.575
0)≈0.067
f(1.562
5)≈0.003
f(1.556
2)≈-0.029
f(1.550
0)≈-0.060
据此数据,可得方程3x-x-4=0的一个近似解为________(精确到0.01)
13.若关于的方程有实数解,则实数的取值范围是________
三、解答题
14.讨论函数f(x)=(ax-1)(x-2)(a∈R)的零点.
15.对于函数().
(Ⅰ)当时,求函数的零点;
(Ⅱ)若对任意实数,函数恒有两个相异的零点,求实数的取值范围
16.已知函数,且.
(1)若在区间上有零点,求实数的取值范围;
(2)若在上的最大值是2,求实数的的值.
参考答案
1.C
【解析】
函数在上为增函数,
又,
则方程的解所在的区间为.
故选:C.
2.B
【解析】
解:
又
由零点存在定理可得在区间存在零点.
方程的根落在区间
故选:B.
3.C
【解析】
根据二分法的思想,函数f(x)在区间[a,b]上的图象连续不断,且f(a)·f(b)<0,即函数的零点是变号零点,才能将区间[a,b]一分为二,逐步得到零点的近似值,对各图象分析可知,A,B,D都符合条件,而选项C不符合,因为图象经过零点时函数值不变号,因此不能用二分法求函数零点.
故选C
4.B
【解析】
由题得,,
而,
根据函数零点存在性定理可得函数在区间上存在零点。
故答案为B.
5.C
【解析】
因为函数的零点个数即方程的根的个数,,
故可化为与图象的交点的个数,
当时,,
,
令,可解的,
所以直线与相切于点,
作出函数与函数图象如图:
由图象可知,函数与函数图象有2个交点,
故函数的零点个数为2个,
故选:C
6.C
【解析】
由题可知:利用二分法求函数与轴交点的横坐标该函数的零点必须是变号零点,
所以根据这个条件可知,不宜用二分法求交点横坐标的是选项C
故选:C
7.C
【解析】
解:能用二分法求零点的函数必须在给定区间[a,b]上连续不断,并且有f(a)?f(b)<0A、B中不存在f(x)<0,D中函数不连续.
故选C.
8.A
【解析】
令,即,显然该方程无解,即函数的零点个数为0;故选A.
9.C
【解析】
结合图象可得:ABD选项每个区间的两个端点函数值异号,可以用二分法求出零点,
C选项区间两个端点函数值同号,不能用二分法求零点.
故选:C
10.B
【解析】
B选项中的零点不是变号零点,
该零点不宜用二分法求解,
故选:B.
11.
【解析】
,表示以圆的为圆心,半径为1的圆的上半部分,
表示斜率为1的一组平行线,
半圆与直线有两个交点,
直线与半圆相切时,
当这两个函数图象由两个交点时,根据图象,
纵截距的取值范围是,故答案为.
12.1.56
【解析】
注意到f(1.5562)=-0.029和f(1.5625)=0.003,显然f(1.5562)f(1.5625)<0,故区间的端点四舍五入可得1.56.
13.
【解析】
因为可化为,
又,
当且仅当,即时,取等号;
又关于的方程有实数解,
所以只需,
解得:.
故答案为:
14.详见解析.
【解析】
试题分析:根据函数解析式中a的情况可分三种情况①一次函数,②二次函数一个零点③二次函数两个零点讨论,将问题转化为求一元二次方程的根,就是函数的零点.
试题解析:当a=0时,函数为y=-x+2,则其零点为x=2.
当a=时,则由
(x-2)=0,
解得x1=x2=2,则其零点为x=2.
当a≠0且a≠时,则由(ax-1)(x-2)=0,
解得x=或x=2,
综上所述当a=0时,零点为x=2;
当a=时,零点为x=2.
当a≠0且a≠时,零点为x=和x=2.
15.(Ⅰ);(Ⅱ).
【解析】
试题分析:(Ⅰ)当时,,所以由可得;
(Ⅱ)由函数恒有两个相异的零点,得恒成立,即对于恒成立,这是一个关于的二次不等式,所以,即可解得.
试题解析:(Ⅰ)当时,代入得,所以由可得,所以函数的零点为;
(Ⅱ)由题意可得,则对于恒成立,所以,从而解得.
16.(1);(2)或.
【解析】
试题分析:(1)由,得.又在区间上有零点可得.或者可用求根公式求得另一零点,使其在区间内.
(2)函数的图像是开口向上的抛物线,对称轴为.讨论对称轴与区间的关系,根据函数的单调性求其最大值.
试题解析:解:(1)由,得.
又在区间上有零点,且的一个零点是1;
所以,.
(2),对称轴为.
①当时,,则;
②当时,,则,或(舍去);
③当时,,则(舍去);
综上:或.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
2020-2021学年度高中数学必修一
二分法与函数的零点同步训练
第I卷(选择题)
一、单选题
1.设函数,
在用二分法求方程在内的近似解过程中得,则方程的解所在的区间是(
)
A.
B.
C.
D.
2.设,用二分法求方程在内近似解的过程中得,,,则方程的根落在区间
A.
B.
C.
D.不能确定
3.以下每个图象表示的函数都有零点,但不能用二分法求函数零点的是( )
A.
B.
C.
D.
4.函数的零点必落在区间(
)
A.
B.
C.
D.
5.函数的零点个数为(
)
A.
B.
C.
D.
6.下列函数的图象均与轴有交点,其中不宜用二分法求交点横坐标的是(
).
A.
B.
C.
D.
7.下列函数图像与x轴均有公共点,其中能用二分法求零点的是( )
A.
B.
C.
D.
8.函数f(x)=x+的零点个数为( )
A.0
B.1
C.2
D.3
9.如图是函数f(x)的图象,它与x轴有4个不同的公共点.给出的下列四个区间之中,存在不能用二分法求出的零点,该零点所在的区间是(
)
A.[-2.1,-1]
B.[4.1,5]
C.[1.9,2.3]
D.[5,6.1]
10.下列函数图像与x轴均有交点,但不宜用二分法求函数的零点的是(
)
A.
B.
C.
D.
第II卷(非选择题)
二、填空题
11.若方程有两个不等的实根,则b的取值范围是_____________
.
12.用二分法求函数f(x)=3x-x-4的一个零点,其参考数据如下:
f(1.600
0)≈0.200
f(1.587
5)≈0.133
f(1.575
0)≈0.067
f(1.562
5)≈0.003
f(1.556
2)≈-0.029
f(1.550
0)≈-0.060
据此数据,可得方程3x-x-4=0的一个近似解为________(精确到0.01)
13.若关于的方程有实数解,则实数的取值范围是________
三、解答题
14.讨论函数f(x)=(ax-1)(x-2)(a∈R)的零点.
15.对于函数().
(Ⅰ)当时,求函数的零点;
(Ⅱ)若对任意实数,函数恒有两个相异的零点,求实数的取值范围
16.已知函数,且.
(1)若在区间上有零点,求实数的取值范围;
(2)若在上的最大值是2,求实数的的值.
参考答案
1.C
【解析】
函数在上为增函数,
又,
则方程的解所在的区间为.
故选:C.
2.B
【解析】
解:
又
由零点存在定理可得在区间存在零点.
方程的根落在区间
故选:B.
3.C
【解析】
根据二分法的思想,函数f(x)在区间[a,b]上的图象连续不断,且f(a)·f(b)<0,即函数的零点是变号零点,才能将区间[a,b]一分为二,逐步得到零点的近似值,对各图象分析可知,A,B,D都符合条件,而选项C不符合,因为图象经过零点时函数值不变号,因此不能用二分法求函数零点.
故选C
4.B
【解析】
由题得,,
而,
根据函数零点存在性定理可得函数在区间上存在零点。
故答案为B.
5.C
【解析】
因为函数的零点个数即方程的根的个数,,
故可化为与图象的交点的个数,
当时,,
,
令,可解的,
所以直线与相切于点,
作出函数与函数图象如图:
由图象可知,函数与函数图象有2个交点,
故函数的零点个数为2个,
故选:C
6.C
【解析】
由题可知:利用二分法求函数与轴交点的横坐标该函数的零点必须是变号零点,
所以根据这个条件可知,不宜用二分法求交点横坐标的是选项C
故选:C
7.C
【解析】
解:能用二分法求零点的函数必须在给定区间[a,b]上连续不断,并且有f(a)?f(b)<0A、B中不存在f(x)<0,D中函数不连续.
故选C.
8.A
【解析】
令,即,显然该方程无解,即函数的零点个数为0;故选A.
9.C
【解析】
结合图象可得:ABD选项每个区间的两个端点函数值异号,可以用二分法求出零点,
C选项区间两个端点函数值同号,不能用二分法求零点.
故选:C
10.B
【解析】
B选项中的零点不是变号零点,
该零点不宜用二分法求解,
故选:B.
11.
【解析】
,表示以圆的为圆心,半径为1的圆的上半部分,
表示斜率为1的一组平行线,
半圆与直线有两个交点,
直线与半圆相切时,
当这两个函数图象由两个交点时,根据图象,
纵截距的取值范围是,故答案为.
12.1.56
【解析】
注意到f(1.5562)=-0.029和f(1.5625)=0.003,显然f(1.5562)f(1.5625)<0,故区间的端点四舍五入可得1.56.
13.
【解析】
因为可化为,
又,
当且仅当,即时,取等号;
又关于的方程有实数解,
所以只需,
解得:.
故答案为:
14.详见解析.
【解析】
试题分析:根据函数解析式中a的情况可分三种情况①一次函数,②二次函数一个零点③二次函数两个零点讨论,将问题转化为求一元二次方程的根,就是函数的零点.
试题解析:当a=0时,函数为y=-x+2,则其零点为x=2.
当a=时,则由
(x-2)=0,
解得x1=x2=2,则其零点为x=2.
当a≠0且a≠时,则由(ax-1)(x-2)=0,
解得x=或x=2,
综上所述当a=0时,零点为x=2;
当a=时,零点为x=2.
当a≠0且a≠时,零点为x=和x=2.
15.(Ⅰ);(Ⅱ).
【解析】
试题分析:(Ⅰ)当时,,所以由可得;
(Ⅱ)由函数恒有两个相异的零点,得恒成立,即对于恒成立,这是一个关于的二次不等式,所以,即可解得.
试题解析:(Ⅰ)当时,代入得,所以由可得,所以函数的零点为;
(Ⅱ)由题意可得,则对于恒成立,所以,从而解得.
16.(1);(2)或.
【解析】
试题分析:(1)由,得.又在区间上有零点可得.或者可用求根公式求得另一零点,使其在区间内.
(2)函数的图像是开口向上的抛物线,对称轴为.讨论对称轴与区间的关系,根据函数的单调性求其最大值.
试题解析:解:(1)由,得.
又在区间上有零点,且的一个零点是1;
所以,.
(2),对称轴为.
①当时,,则;
②当时,,则,或(舍去);
③当时,,则(舍去);
综上:或.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
