3.2函数的增长率与函数模型 同步训练(含解析)
文档属性
| 名称 | 3.2函数的增长率与函数模型 同步训练(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2020-2021学年度高中数学必修一
函数的增长率与函数模型同步训练
第I卷(选择题)
一、单选题
1.某同学最近5年内的学习费用y(千元)与时间x(年)的关系如图所示,则可选择的模拟函数模型是(
)
A.y=ax+b
B.y=ax2+bx+c
C.y=aex+b
D.y=aln
x+b
2.下列函数中,随x的增大,增长速度最快的是(
)
A.
B.
C.
D.
3.高为、满缸水量为的鱼缸的轴截面如图所示,现底部有一个小洞,满缸水从洞中流出,若鱼缸水深为时水的体积为,则函数的大致图像是(
)
A.
B.
C.
D.
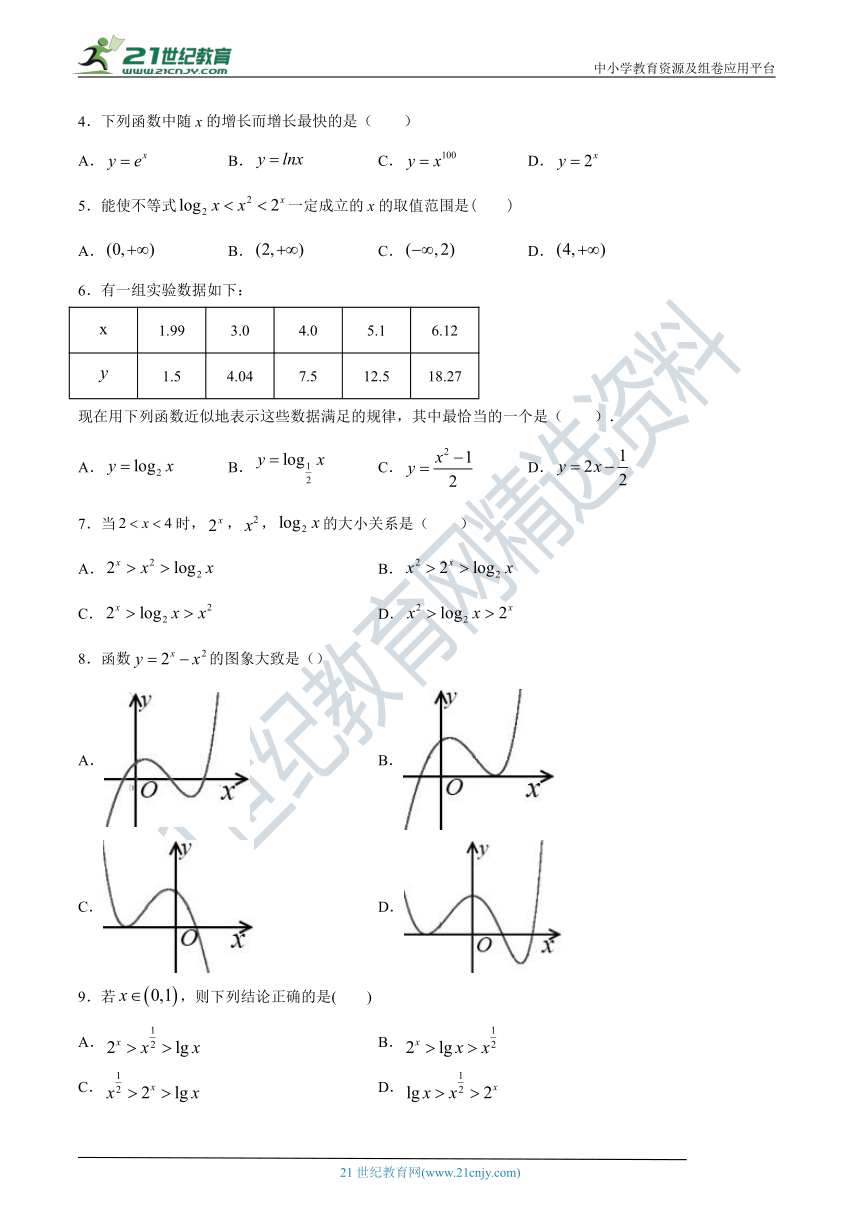
4.下列函数中随x的增长而增长最快的是(
)
A.
B.
C.
D.
5.能使不等式一定成立的x的取值范围是(
)
A.
B.
C.
D.
6.有一组实验数据如下:
1.99
3.0
4.0
5.1
6.12
1.5
4.04
7.5
12.5
18.27
现在用下列函数近似地表示这些数据满足的规律,其中最恰当的一个是(
).
A.
B.
C.
D.
7.当时,,,的大小关系是(
)
A.
B.
C.
D.
8.函数的图象大致是()
A.
B.
C.
D.
9.若,则下列结论正确的是( )
A.
B.
C.
D.
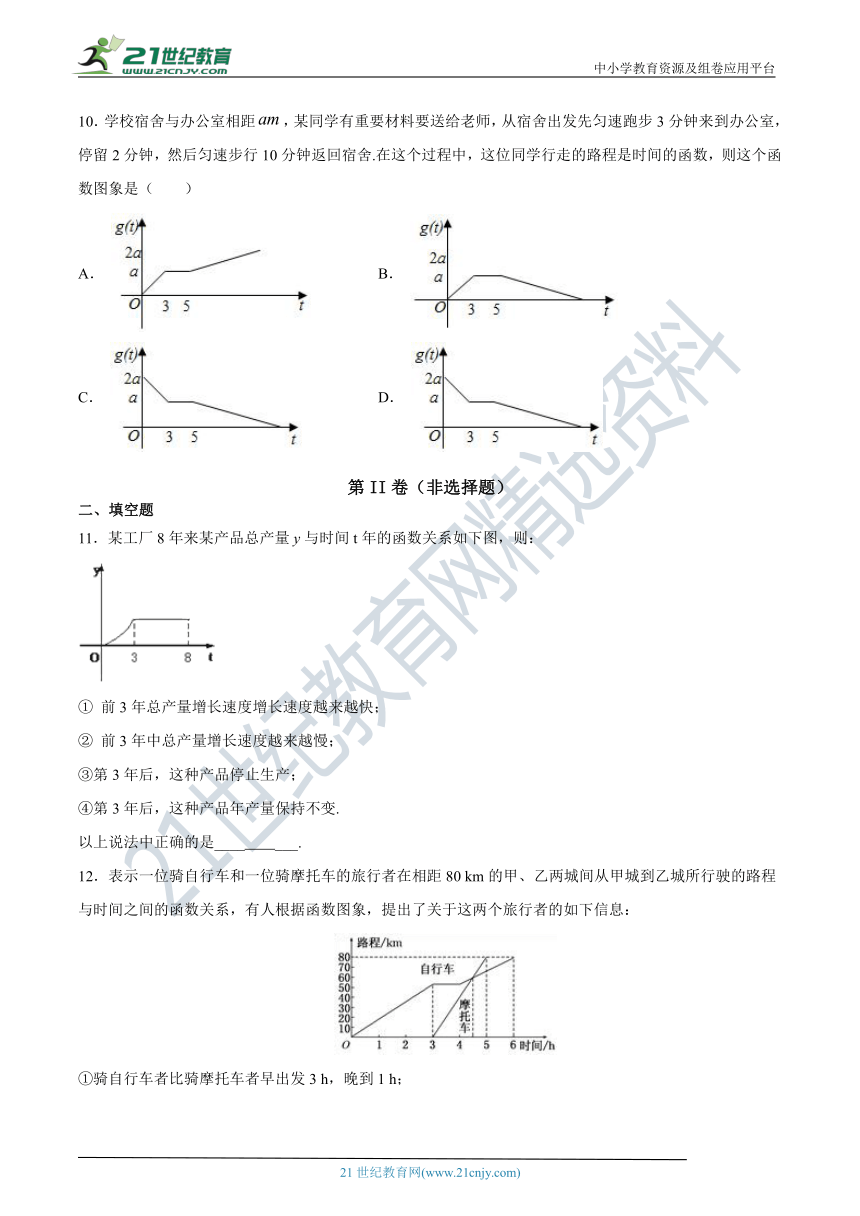
10.学校宿舍与办公室相距,某同学有重要材料要送给老师,从宿舍出发先匀速跑步3分钟来到办公室,停留2分钟,然后匀速步行10分钟返回宿舍.在这个过程中,这位同学行走的路程是时间的函数,则这个函数图象是(
)
A.
B.
C.
D.
第II卷(非选择题)
二、填空题
11.某工厂8年来某产品总产量y与时间t年的函数关系如下图,则:
①
前3年总产量增长速度增长速度越来越快;
②
前3年中总产量增长速度越来越慢;
③第3年后,这种产品停止生产;
④第3年后,这种产品年产量保持不变.
以上说法中正确的是____
___.
12.表示一位骑自行车和一位骑摩托车的旅行者在相距80
km的甲、乙两城间从甲城到乙城所行驶的路程与时间之间的函数关系,有人根据函数图象,提出了关于这两个旅行者的如下信息:
①骑自行车者比骑摩托车者早出发3
h,晚到1
h;
②骑自行车者是变速运动,骑摩托车者是匀速运动;
③骑摩托车者在出发1.5
h后追上了骑自行车者;
④骑摩托车者在出发1.5
h后与骑自行车者速度一样.
其中,正确信息的序号是________.
13.
在不考虑空气阻力的情况下,火箭的最大速度v(米/秒)和燃料的质量M(千克)、火箭(除燃料外)的质量m(千克)的函数关系式是v=2
000·ln.当燃料质量是火箭质量的________倍时,火箭的最大速度可达12千米/秒.
三、解答题
14.某市近郊有一块大约的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为平方米.
(1)分别用表示和的函数关系式,并给出定义域;
(2)怎样设计能使取得最大值,并求出最大值.
15.食品安全问题越来越引起人们的重视,农药、化肥的滥用对人民群众的健康带来一定的危害,为了给消费者带来放心的蔬菜,某农村合作社每年投入200万元,搭建了甲、乙两个无公害蔬菜大棚,每个大棚至少要投入20万元,其中甲大棚种西红柿,乙大棚种黄瓜,根据以往的种菜经验,发现种西红柿的年收益P、种黄瓜的年收益Q与投入a(单位:万元)满足P=80++120.设甲大棚的投入为x(单位:万元),每年两个大棚的总收益为f(x)(单位:万元).
(1)求f(50)的值;
(2)试问如何安排甲、乙两个大棚的投入,才能使总收益f(x)最大?
16.某市由甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同,甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.某公司准备下个月从两家中的一家租一张球台开展活动,活动时间不少于15小时,也不超过40小时,设在甲家租一张球台开展活动小时的收费为元,在乙家租一张球台开展活动小时的收费为元.
(1)写出与的解析式;
(2)选择哪家比较合算?请说明理由.
17.某公司拟投资100万元,有两种投资方案可供选择:一种是年利率为10%,按单利计算,5年后收回本金和利息;另一种是年利率为9%,按每年复利一次计算,5年后收回本金和利息.哪一种投资更有利?这种投资比另一种投资5年可多得利息多少元?(结果精确到0.01万元)
参考答案
1.B
【解析】
从所给的散点图可看出函数的变化趋势是先增后减,所以该函数模型是二次函数.
故选:B
2.C
【解析】
随x的增大,指数函数的增长速度最快,
的增长速度最快,
故选:C.
3.B
【解析】
根据题意知,函数的自变量为水深,函数值为鱼缸中水的体积,所以当时,体积,所以函数图像过原点,故排除A、C;
再根据鱼缸的形状,下边较细,中间较粗,上边较细,所以随着水深的增加,体积的变化速度是先慢后快再慢的,故选B.
4.A
【解析】
由于是指数函数,是对数函数,是幂函数,指数函数,
由于当x足够大时,指数函数的增长速度最快,呈爆炸式增长,且2个指数函数的底数分别为e?和
2,且,故增长速度最快的是.
故选:A.
5.D
【解析】
作出、(红色)、图像
由图像可知,当时,
故选:D.
6.C
【解析】
对于A选项,时,,与表格差距较大,故排除
对于B选项,时,,与表格差距较大,故排除
对于C选项,时,
对于D选项,时,,相对于C项误差较大,故排除
故选:C
7.B
【解析】
在平面直角坐标系中,作出,,在时的图象如下图所示:
由图象可知,当时,
故选
8.A
【解析】
因为2、4是函数的零点,所以排除B、C;
因为时,所以排除D,故选A
9.A
【解析】
如图所示,结合,及的图象易知,当时,,
本题选择A选项.
10.A
【解析】
由题意可得先匀速跑步3分钟来到办公室,路程是递增,停留2分钟,
路程不发生变化,再匀速步行10分钟返回宿舍,总路程也是增加的,只有A符合,
故选:A.
11.①③
【解析】
由函数图象可知
在区间上,图象图象凹陷上升的,表明年产量增长速度越来越快;
在区间上,如果图象是水平直线,表明总产量保持不变,即年产量为0.
①、③正确
故答案为:①③
12.①②③
【解析】
看时间轴易知①正确;骑摩托车者行驶的路程与时间的函数图象是直线,所以是匀速运动,而骑自行车者行驶的路程与时间的函数图象是折线,所以是变速运动,因此②正确;两条曲线的交点的横坐标对应着4.5,故③正确,④错误.
故答案为①②③.
点睛:研究函数问题离不开函数图象,函数图象反映了函数的所有性质,在研究函数问题时要时时刻刻想到函数的图象,学会从函数图象上去分析问题、寻找解决问题的方法.
13.
【解析】
由题意可得12000=2000,=6,解得,所以,填
14.(1),其定义域是.
(2)设计,时,运动场地面积最大,最大值为2430平方米.
【解析】
解:(1)由已知,,其定义域是.
,
,,
,其定义域是.
(2),
当且仅当,即时,上述不等式等号成立,
此时,,,.
答:设计,时,运动场地面积最大,最大值为2430平方米.
15.(1);(2)甲大棚万元,乙大棚万元时,总收益最大,
且最大收益为万元.
【解析】
试题分析:(1)当甲大棚投入万元,则乙大棚投入万元,此时直接计算即可;(2)列出总收益的函数式得,令,换元将函数转换为关于的二次函数,由二次函数知识可求其最大值及相应的值.
试题解析:
(1)∵甲大棚投入50万元,则乙大棚投入150万元,
∴
(2),
依题得,即,
故.
令,则,
当时,即时,,
∴甲大棚投入128万元,乙大棚投入72万元时,总收益最大,且最大收益为282万元.
16.(1),;
(2)见解析.
【解析】
(1)由题设有,.
(2)令时,解得;
令,解得,
所以:当时,,选甲家比较合算;
当时,,两家一样合算;
当时,,选乙家比较合.
17.按年利率为9%每年复利一次计算的投资方式要比按年利率为10%单利计算的更有利,5年后多得利息3.86万元.
【解析】
试题分析:最优方案问题,方案一的函数模型为,方案二的函数模型为,通过计算,得到方案二获利更多,解得答案.
试题解析:
本金100万元,年利率为10%,按单利计算,5年后的本息和是100×(1+10%×5)=150(万元).
本金100万元,年利率为9%,按每年复利一次计算,5年后的本息和是100×(1+9%)5≈153.86(万元).
由此可见,按年利率为9%每年复利一次计算的投资方式要比按年利率为10%单利计算的更有利,5年后多得利息3.86万元.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
2020-2021学年度高中数学必修一
函数的增长率与函数模型同步训练
第I卷(选择题)
一、单选题
1.某同学最近5年内的学习费用y(千元)与时间x(年)的关系如图所示,则可选择的模拟函数模型是(
)
A.y=ax+b
B.y=ax2+bx+c
C.y=aex+b
D.y=aln
x+b
2.下列函数中,随x的增大,增长速度最快的是(
)
A.
B.
C.
D.
3.高为、满缸水量为的鱼缸的轴截面如图所示,现底部有一个小洞,满缸水从洞中流出,若鱼缸水深为时水的体积为,则函数的大致图像是(
)
A.
B.
C.
D.
4.下列函数中随x的增长而增长最快的是(
)
A.
B.
C.
D.
5.能使不等式一定成立的x的取值范围是(
)
A.
B.
C.
D.
6.有一组实验数据如下:
1.99
3.0
4.0
5.1
6.12
1.5
4.04
7.5
12.5
18.27
现在用下列函数近似地表示这些数据满足的规律,其中最恰当的一个是(
).
A.
B.
C.
D.
7.当时,,,的大小关系是(
)
A.
B.
C.
D.
8.函数的图象大致是()
A.
B.
C.
D.
9.若,则下列结论正确的是( )
A.
B.
C.
D.
10.学校宿舍与办公室相距,某同学有重要材料要送给老师,从宿舍出发先匀速跑步3分钟来到办公室,停留2分钟,然后匀速步行10分钟返回宿舍.在这个过程中,这位同学行走的路程是时间的函数,则这个函数图象是(
)
A.
B.
C.
D.
第II卷(非选择题)
二、填空题
11.某工厂8年来某产品总产量y与时间t年的函数关系如下图,则:
①
前3年总产量增长速度增长速度越来越快;
②
前3年中总产量增长速度越来越慢;
③第3年后,这种产品停止生产;
④第3年后,这种产品年产量保持不变.
以上说法中正确的是____
___.
12.表示一位骑自行车和一位骑摩托车的旅行者在相距80
km的甲、乙两城间从甲城到乙城所行驶的路程与时间之间的函数关系,有人根据函数图象,提出了关于这两个旅行者的如下信息:
①骑自行车者比骑摩托车者早出发3
h,晚到1
h;
②骑自行车者是变速运动,骑摩托车者是匀速运动;
③骑摩托车者在出发1.5
h后追上了骑自行车者;
④骑摩托车者在出发1.5
h后与骑自行车者速度一样.
其中,正确信息的序号是________.
13.
在不考虑空气阻力的情况下,火箭的最大速度v(米/秒)和燃料的质量M(千克)、火箭(除燃料外)的质量m(千克)的函数关系式是v=2
000·ln.当燃料质量是火箭质量的________倍时,火箭的最大速度可达12千米/秒.
三、解答题
14.某市近郊有一块大约的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为平方米.
(1)分别用表示和的函数关系式,并给出定义域;
(2)怎样设计能使取得最大值,并求出最大值.
15.食品安全问题越来越引起人们的重视,农药、化肥的滥用对人民群众的健康带来一定的危害,为了给消费者带来放心的蔬菜,某农村合作社每年投入200万元,搭建了甲、乙两个无公害蔬菜大棚,每个大棚至少要投入20万元,其中甲大棚种西红柿,乙大棚种黄瓜,根据以往的种菜经验,发现种西红柿的年收益P、种黄瓜的年收益Q与投入a(单位:万元)满足P=80++120.设甲大棚的投入为x(单位:万元),每年两个大棚的总收益为f(x)(单位:万元).
(1)求f(50)的值;
(2)试问如何安排甲、乙两个大棚的投入,才能使总收益f(x)最大?
16.某市由甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同,甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.某公司准备下个月从两家中的一家租一张球台开展活动,活动时间不少于15小时,也不超过40小时,设在甲家租一张球台开展活动小时的收费为元,在乙家租一张球台开展活动小时的收费为元.
(1)写出与的解析式;
(2)选择哪家比较合算?请说明理由.
17.某公司拟投资100万元,有两种投资方案可供选择:一种是年利率为10%,按单利计算,5年后收回本金和利息;另一种是年利率为9%,按每年复利一次计算,5年后收回本金和利息.哪一种投资更有利?这种投资比另一种投资5年可多得利息多少元?(结果精确到0.01万元)
参考答案
1.B
【解析】
从所给的散点图可看出函数的变化趋势是先增后减,所以该函数模型是二次函数.
故选:B
2.C
【解析】
随x的增大,指数函数的增长速度最快,
的增长速度最快,
故选:C.
3.B
【解析】
根据题意知,函数的自变量为水深,函数值为鱼缸中水的体积,所以当时,体积,所以函数图像过原点,故排除A、C;
再根据鱼缸的形状,下边较细,中间较粗,上边较细,所以随着水深的增加,体积的变化速度是先慢后快再慢的,故选B.
4.A
【解析】
由于是指数函数,是对数函数,是幂函数,指数函数,
由于当x足够大时,指数函数的增长速度最快,呈爆炸式增长,且2个指数函数的底数分别为e?和
2,且,故增长速度最快的是.
故选:A.
5.D
【解析】
作出、(红色)、图像
由图像可知,当时,
故选:D.
6.C
【解析】
对于A选项,时,,与表格差距较大,故排除
对于B选项,时,,与表格差距较大,故排除
对于C选项,时,
对于D选项,时,,相对于C项误差较大,故排除
故选:C
7.B
【解析】
在平面直角坐标系中,作出,,在时的图象如下图所示:
由图象可知,当时,
故选
8.A
【解析】
因为2、4是函数的零点,所以排除B、C;
因为时,所以排除D,故选A
9.A
【解析】
如图所示,结合,及的图象易知,当时,,
本题选择A选项.
10.A
【解析】
由题意可得先匀速跑步3分钟来到办公室,路程是递增,停留2分钟,
路程不发生变化,再匀速步行10分钟返回宿舍,总路程也是增加的,只有A符合,
故选:A.
11.①③
【解析】
由函数图象可知
在区间上,图象图象凹陷上升的,表明年产量增长速度越来越快;
在区间上,如果图象是水平直线,表明总产量保持不变,即年产量为0.
①、③正确
故答案为:①③
12.①②③
【解析】
看时间轴易知①正确;骑摩托车者行驶的路程与时间的函数图象是直线,所以是匀速运动,而骑自行车者行驶的路程与时间的函数图象是折线,所以是变速运动,因此②正确;两条曲线的交点的横坐标对应着4.5,故③正确,④错误.
故答案为①②③.
点睛:研究函数问题离不开函数图象,函数图象反映了函数的所有性质,在研究函数问题时要时时刻刻想到函数的图象,学会从函数图象上去分析问题、寻找解决问题的方法.
13.
【解析】
由题意可得12000=2000,=6,解得,所以,填
14.(1),其定义域是.
(2)设计,时,运动场地面积最大,最大值为2430平方米.
【解析】
解:(1)由已知,,其定义域是.
,
,,
,其定义域是.
(2),
当且仅当,即时,上述不等式等号成立,
此时,,,.
答:设计,时,运动场地面积最大,最大值为2430平方米.
15.(1);(2)甲大棚万元,乙大棚万元时,总收益最大,
且最大收益为万元.
【解析】
试题分析:(1)当甲大棚投入万元,则乙大棚投入万元,此时直接计算即可;(2)列出总收益的函数式得,令,换元将函数转换为关于的二次函数,由二次函数知识可求其最大值及相应的值.
试题解析:
(1)∵甲大棚投入50万元,则乙大棚投入150万元,
∴
(2),
依题得,即,
故.
令,则,
当时,即时,,
∴甲大棚投入128万元,乙大棚投入72万元时,总收益最大,且最大收益为282万元.
16.(1),;
(2)见解析.
【解析】
(1)由题设有,.
(2)令时,解得;
令,解得,
所以:当时,,选甲家比较合算;
当时,,两家一样合算;
当时,,选乙家比较合.
17.按年利率为9%每年复利一次计算的投资方式要比按年利率为10%单利计算的更有利,5年后多得利息3.86万元.
【解析】
试题分析:最优方案问题,方案一的函数模型为,方案二的函数模型为,通过计算,得到方案二获利更多,解得答案.
试题解析:
本金100万元,年利率为10%,按单利计算,5年后的本息和是100×(1+10%×5)=150(万元).
本金100万元,年利率为9%,按每年复利一次计算,5年后的本息和是100×(1+9%)5≈153.86(万元).
由此可见,按年利率为9%每年复利一次计算的投资方式要比按年利率为10%单利计算的更有利,5年后多得利息3.86万元.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
