2020年北师大版七年级数学上册3.2 《代数式》课件(共25张ppt)
文档属性
| 名称 | 2020年北师大版七年级数学上册3.2 《代数式》课件(共25张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 345.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-11 12:34:56 | ||
图片预览





文档简介
整式及其加减
第三章
北师大版七年级数学上册
3.2 代数式
上节课我们通过用火柴棒拼摆如图所示的正方形.
找到了拼摆正方形的个数与所用火柴棒根数之间的数量关系,并引进了字母,即用字母表示数来表达了这个问题的数量关系.想一想:如何用字母表示这个数量关系?
搭x个这样的正方形需要火柴棒根数:[4+3(x-1)]根,或[x+x+(x+1)]根,或(1+3x)根等.
引入课题
用字母表示下列数量关系:
1.长为a m , 宽为b m 的长方形的周长是___m ,面积是__________m2 .
2.边长为a m 的立方体的体积是___ m3.
3.小亮用t秒走了s米,他的速度为___米/秒.
2(a+b)
ab
a3
t
s
注:运算符号包括加.减.乘.除.乘方及开方 .
像4+3(x-1), x+x+(x+1), 2(a+b), ab, , 等式子都是代数式.它们就是用基本的运算符号把数和字母连接而成的,单独一个数或一个字母也是代数式.
t
s
给出概念
复习
1.一个两位数的个位数字是a,十位数字是b,请用代数式表示这个两位数;
2.如何用代数式表示一个三位数?
3.代数式(1+8%)x可以表示什么?
4.用具体数值代替(1+8%)x中的x,并解释所得代数式值的意义.
5.f的11倍再加上2可以表示为_____.
6.数a的1/8与这个数的和可以表示为_____.
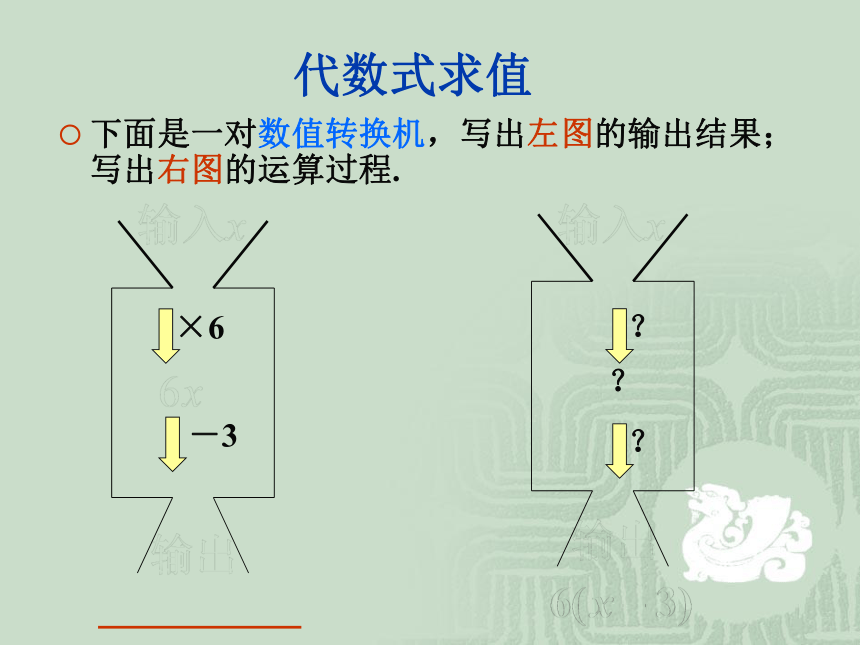
代数式求值
下面是一对数值转换机,写出左图的输出结果;写出右图的运算过程.
×6
-3
?
?
?
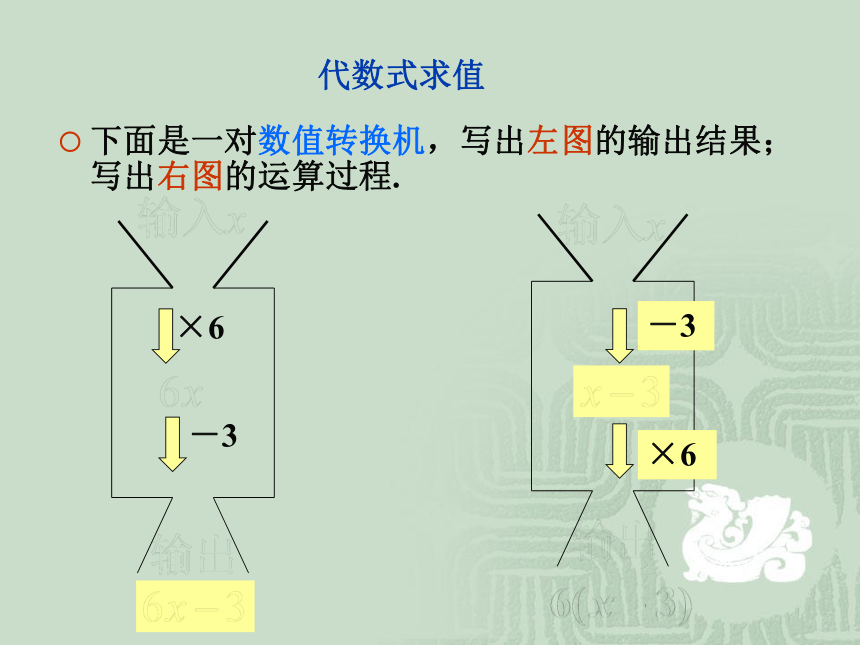
代数式求值
下面是一对数值转换机,写出左图的输出结果;写出右图的运算过程.
×6
-3
-3
×6
输入
-2
- 1/2
0
0.26
1/3
5/2
4.5
图1的输出
图2的输出
-15
-6
-3
-1.44
-1
12
24
-30
-21
-18
-16.44
-16
-3
9
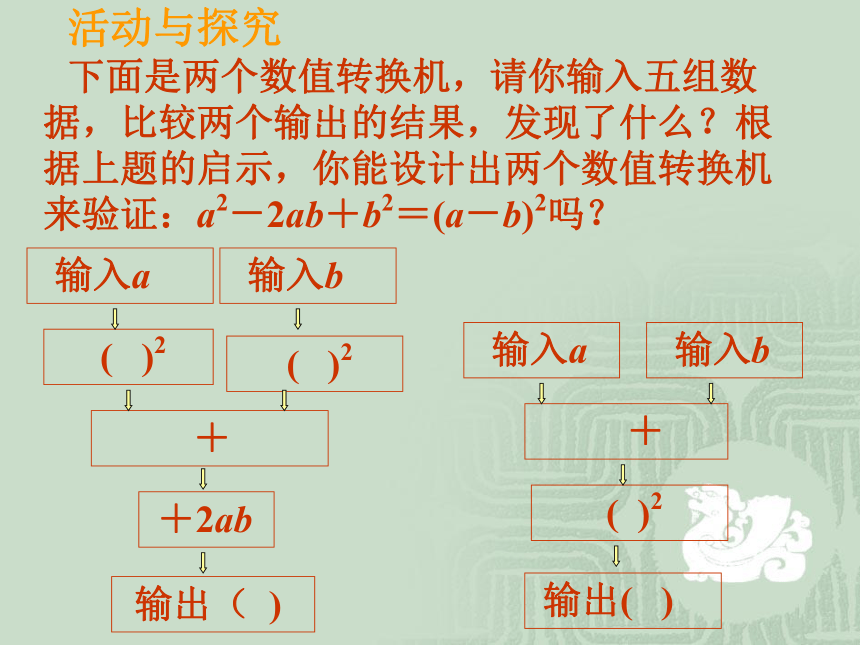
活动与探究
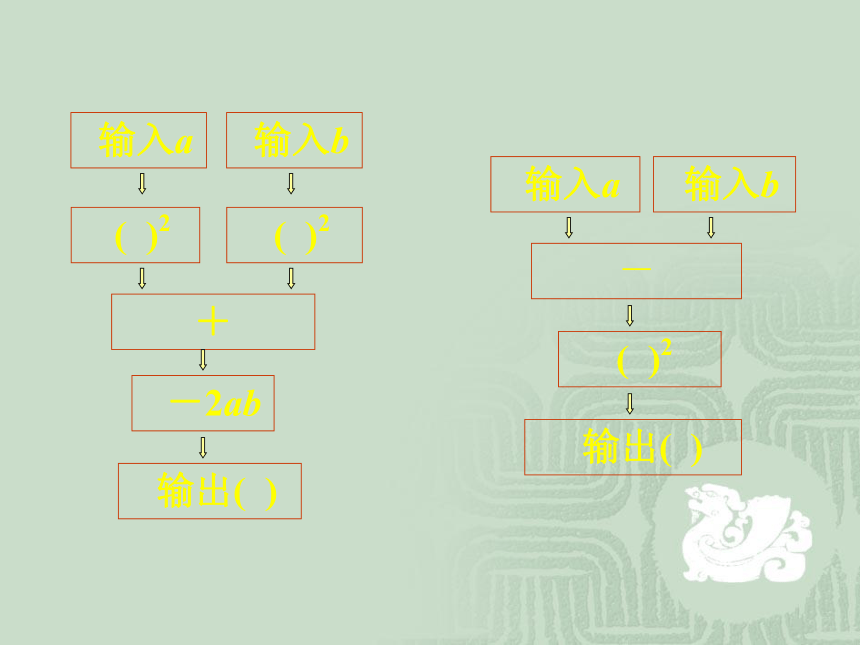
下面是两个数值转换机,请你输入五组数据,比较两个输出的结果,发现了什么?根据上题的启示,你能设计出两个数值转换机来验证:a2-2ab+b2=(a-b)2吗?
输入a
输入b
( )2
+2ab
输出( )
+
( )2
输入b
( )2
输出( )
+
输入a
输入a
输入b
( )2
-2ab
输出( )
+
( )2
输入b
( )2
输出( )
-
输入a
填写下表,并观察下列两个代数式的值的变化情况
n
1
2
3
4
5
6
7
8
5n+6
16
11
21
26
31
36
41
46
1
4
9
16
25
36
49
64
思考
(1)随着n的值逐渐变大,两个代数式的值如何变化?
(2)估计一下,哪个代数式的值先超过100.
例题
(1)某公园的门票价格是:成人票每张10元,学生票每张5元.一个旅游团有成人x人.学生y人,那么该旅游团应付多少门票费?
解:该旅游团应付的门票费是(10x + 5y)元.
(2)如果该旅游团有37个成人.15个学生,那么他们应付多少门票费?
解:把x =37, y=15代入代数式10x+5y,得
10×37+5×15=445.
因此,他们应付445元门票费.
例1:列出代数式,并求值.
想一想:代数式10x+5y可以表示什么?
如果用x(米/ 秒)表示小明跑步的速度,用y(米/秒)表示小明走路的速度,那么10 x+5y表示他跑步10秒和走路5秒所经过的路程.
如果用x和y分别表示1元和5角硬币的枚数,那么10 x+5y就表示x枚1元硬币和y枚5角硬币共是多少角钱.
我国载人飞船的造价约为10亿,人造卫星造价约为5亿,在未来的二十年内将造x架载人飞船,和y架人造卫星,那么10x+5y就表示造x架载人飞船和y架人造卫星共需花的钱.
在某地,人们发现某种蟋蟀叫的次数与温度之间有如下的近似关系:用蟋蟀1分钟叫的次数除以7,然后再加上3,就近似地得到该地当时的温度(℃).
(1) 用代数式表示该地当时的温度;
(2) 当蟋蟀1分钟叫的次数分别是80,100和120时,该地当时的温度约是多少?
例2
(1) 张宇身高1.2 米,在某时刻测得他影子的长度
是2 米.此时张宇的身高是他影长的多少倍?
(2)如果用l 表示物体的影长,那么如何用代数式
表示此时此地物体的高度?
(3) 该地某建筑物影长 5.5 米,此时它的高度是
多少米?
例3
解: (1)1.2÷2= ,即此时张宇的身高是他影
长的 倍.
5
3
5
3
(2)此时此地物体的高度为 米.
l
5
3
(3)将l=5.5代入 , 得 ×5.5=3.3(米).
l
5
3
5
3
因此,建筑物此时的高度是3.3米.
随n的值的增大,每个代数式的值都是增加的趋势.
n2的值先超过100,因为在n=6时,n2的值就开始超过5n+6的值.
由代数式求值可以推断每个代数式所反映的规律,不同的代数式反映的规律不同.
结论:
课堂练习
1. 根据下面a.b的值,求代数式 的值.
(1) ; (2)
从填好的表中,你发现了什么规律?若发现了,请
写在下面的横线上_________.
2. 填表
2
1
1/2
0
人体血液的质量约占体重的6%-7.5%.
(1)如果某人体重是a千克,那么他的血液质量大约在什么范围内?
(2)亮亮体重是40千克,他的血液质量大约在什么范围内?
(3)估计你自己的血液质量.
算一算:
物体自由下落的高度h(米)和下落时间t(秒)的关系,在地球上大约是:
h=4.9 t2,在月球上大约是:h=0.8 t2.
(1)填写下表
(2)物体在哪儿下落得快?
(3)当h=20米时,比较物体在地球上和月球上自由下落所需的时间.
t
0
2
4
6
8
10
h=4.9t2
h=0.8t2
t
0
2
4
6
8
10
h=4.9t2
0
19.6
78.4
176.4
313.6
490
h=0.8t2
0
3.2
12.8
28.8
51.2
80
通过表格我们可估计
t(地球)≈2秒,t(月球)≈5秒
游戏1
班级同学按4个同学一组进行分组,做一个传数游戏.第一个同学任意报一个数给第二个同学,第二个同学把这个数加1传给第三个同学,第三个同学再把听到的数平方后传给第四个同学,第四个同学把听到的数减去1报出答案.
(1)如果第一个同学报给第二个同学的数是5,第四个同学报出的答案是35,这个结果对吗?
(2)如果已知第一个同学报给第二个同学的数,你如何最快得出答案?
x
x+1
(x+1)2
(x+1)2-1
游戏2 看谁算的快,猜的准
(1)填表:
x
0.25
0.5
1
10
100
1000
10000
100000
(2)当x非常大时, 的值接近于什么数?
思维拓展:
已知:2x-y=3,
那么4x-3-2y=?
解:原式=2(2x-y)-3
=2×3-3
=3
小结:本节课你的收获是什么?
认识到代数式能把生活中的数和数量之间的关系简明地表示出来,我们可以根据代数式求值推断代数式所反映的规律,从而学会判断事物.估算问题以及用代数知识去解决一些简单问题.
代数式求值就是用数值代替代数式中的字母,按运算法则计算出的结果.
谢谢!
第三章
北师大版七年级数学上册
3.2 代数式
上节课我们通过用火柴棒拼摆如图所示的正方形.
找到了拼摆正方形的个数与所用火柴棒根数之间的数量关系,并引进了字母,即用字母表示数来表达了这个问题的数量关系.想一想:如何用字母表示这个数量关系?
搭x个这样的正方形需要火柴棒根数:[4+3(x-1)]根,或[x+x+(x+1)]根,或(1+3x)根等.
引入课题
用字母表示下列数量关系:
1.长为a m , 宽为b m 的长方形的周长是___m ,面积是__________m2 .
2.边长为a m 的立方体的体积是___ m3.
3.小亮用t秒走了s米,他的速度为___米/秒.
2(a+b)
ab
a3
t
s
注:运算符号包括加.减.乘.除.乘方及开方 .
像4+3(x-1), x+x+(x+1), 2(a+b), ab, , 等式子都是代数式.它们就是用基本的运算符号把数和字母连接而成的,单独一个数或一个字母也是代数式.
t
s
给出概念
复习
1.一个两位数的个位数字是a,十位数字是b,请用代数式表示这个两位数;
2.如何用代数式表示一个三位数?
3.代数式(1+8%)x可以表示什么?
4.用具体数值代替(1+8%)x中的x,并解释所得代数式值的意义.
5.f的11倍再加上2可以表示为_____.
6.数a的1/8与这个数的和可以表示为_____.
代数式求值
下面是一对数值转换机,写出左图的输出结果;写出右图的运算过程.
×6
-3
?
?
?
代数式求值
下面是一对数值转换机,写出左图的输出结果;写出右图的运算过程.
×6
-3
-3
×6
输入
-2
- 1/2
0
0.26
1/3
5/2
4.5
图1的输出
图2的输出
-15
-6
-3
-1.44
-1
12
24
-30
-21
-18
-16.44
-16
-3
9
活动与探究
下面是两个数值转换机,请你输入五组数据,比较两个输出的结果,发现了什么?根据上题的启示,你能设计出两个数值转换机来验证:a2-2ab+b2=(a-b)2吗?
输入a
输入b
( )2
+2ab
输出( )
+
( )2
输入b
( )2
输出( )
+
输入a
输入a
输入b
( )2
-2ab
输出( )
+
( )2
输入b
( )2
输出( )
-
输入a
填写下表,并观察下列两个代数式的值的变化情况
n
1
2
3
4
5
6
7
8
5n+6
16
11
21
26
31
36
41
46
1
4
9
16
25
36
49
64
思考
(1)随着n的值逐渐变大,两个代数式的值如何变化?
(2)估计一下,哪个代数式的值先超过100.
例题
(1)某公园的门票价格是:成人票每张10元,学生票每张5元.一个旅游团有成人x人.学生y人,那么该旅游团应付多少门票费?
解:该旅游团应付的门票费是(10x + 5y)元.
(2)如果该旅游团有37个成人.15个学生,那么他们应付多少门票费?
解:把x =37, y=15代入代数式10x+5y,得
10×37+5×15=445.
因此,他们应付445元门票费.
例1:列出代数式,并求值.
想一想:代数式10x+5y可以表示什么?
如果用x(米/ 秒)表示小明跑步的速度,用y(米/秒)表示小明走路的速度,那么10 x+5y表示他跑步10秒和走路5秒所经过的路程.
如果用x和y分别表示1元和5角硬币的枚数,那么10 x+5y就表示x枚1元硬币和y枚5角硬币共是多少角钱.
我国载人飞船的造价约为10亿,人造卫星造价约为5亿,在未来的二十年内将造x架载人飞船,和y架人造卫星,那么10x+5y就表示造x架载人飞船和y架人造卫星共需花的钱.
在某地,人们发现某种蟋蟀叫的次数与温度之间有如下的近似关系:用蟋蟀1分钟叫的次数除以7,然后再加上3,就近似地得到该地当时的温度(℃).
(1) 用代数式表示该地当时的温度;
(2) 当蟋蟀1分钟叫的次数分别是80,100和120时,该地当时的温度约是多少?
例2
(1) 张宇身高1.2 米,在某时刻测得他影子的长度
是2 米.此时张宇的身高是他影长的多少倍?
(2)如果用l 表示物体的影长,那么如何用代数式
表示此时此地物体的高度?
(3) 该地某建筑物影长 5.5 米,此时它的高度是
多少米?
例3
解: (1)1.2÷2= ,即此时张宇的身高是他影
长的 倍.
5
3
5
3
(2)此时此地物体的高度为 米.
l
5
3
(3)将l=5.5代入 , 得 ×5.5=3.3(米).
l
5
3
5
3
因此,建筑物此时的高度是3.3米.
随n的值的增大,每个代数式的值都是增加的趋势.
n2的值先超过100,因为在n=6时,n2的值就开始超过5n+6的值.
由代数式求值可以推断每个代数式所反映的规律,不同的代数式反映的规律不同.
结论:
课堂练习
1. 根据下面a.b的值,求代数式 的值.
(1) ; (2)
从填好的表中,你发现了什么规律?若发现了,请
写在下面的横线上_________.
2. 填表
2
1
1/2
0
人体血液的质量约占体重的6%-7.5%.
(1)如果某人体重是a千克,那么他的血液质量大约在什么范围内?
(2)亮亮体重是40千克,他的血液质量大约在什么范围内?
(3)估计你自己的血液质量.
算一算:
物体自由下落的高度h(米)和下落时间t(秒)的关系,在地球上大约是:
h=4.9 t2,在月球上大约是:h=0.8 t2.
(1)填写下表
(2)物体在哪儿下落得快?
(3)当h=20米时,比较物体在地球上和月球上自由下落所需的时间.
t
0
2
4
6
8
10
h=4.9t2
h=0.8t2
t
0
2
4
6
8
10
h=4.9t2
0
19.6
78.4
176.4
313.6
490
h=0.8t2
0
3.2
12.8
28.8
51.2
80
通过表格我们可估计
t(地球)≈2秒,t(月球)≈5秒
游戏1
班级同学按4个同学一组进行分组,做一个传数游戏.第一个同学任意报一个数给第二个同学,第二个同学把这个数加1传给第三个同学,第三个同学再把听到的数平方后传给第四个同学,第四个同学把听到的数减去1报出答案.
(1)如果第一个同学报给第二个同学的数是5,第四个同学报出的答案是35,这个结果对吗?
(2)如果已知第一个同学报给第二个同学的数,你如何最快得出答案?
x
x+1
(x+1)2
(x+1)2-1
游戏2 看谁算的快,猜的准
(1)填表:
x
0.25
0.5
1
10
100
1000
10000
100000
(2)当x非常大时, 的值接近于什么数?
思维拓展:
已知:2x-y=3,
那么4x-3-2y=?
解:原式=2(2x-y)-3
=2×3-3
=3
小结:本节课你的收获是什么?
认识到代数式能把生活中的数和数量之间的关系简明地表示出来,我们可以根据代数式求值推断代数式所反映的规律,从而学会判断事物.估算问题以及用代数知识去解决一些简单问题.
代数式求值就是用数值代替代数式中的字母,按运算法则计算出的结果.
谢谢!
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
