不等关系与不等式
图片预览






文档简介
(共15张PPT)
欢迎光临
现实世界和日常生活中,既有相等关系,又存在着大量的不等关系.如两点之间线段最短,三角形两边之和大于第三边,等等.人们还经常用长与短、高与矮、轻与重、大与小、不超过或不少于等来描述某种客观事物在数量上存在的不等关系。
课程导入
讲授新课
一、不等关系是普遍存在的
想一想, 举出几个现实生活中与不等关系有关的例子
限速10km/h的路标,指示司机前方路段行驶时,应使汽车的速度v不超过10km/h.表示出不等关系是 。
V≤10
1、不等式定义
用不等号(<、>、≤、≥、≠)表示不等关系的式子叫不等式。用“<”或“>”连接的不等式叫严格不等式,用“≤”或“≥”连接的不等式叫非严格不等式。
二、用不等式(组)来表示不等关系
问题1 设点A与平面的距离为d, B为平面上的任意一点,则可得到不等式.
二、用不等式(组)来表示不等关系
答案:d≤|AB|
问题2 今天的天气预报说:明天早晨最低温度为9℃,明天白天的最高温度为16℃ ,那么明天白天的温度t℃满足什么关系?
答案: 9≤t≤16
二、用不等式(组)来表示不等关系
问题3 某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍。怎样写出满足上述所有不等关系的不等式呢?
分析:设截得500mm的钢管x根,截得600mm的钢管y根,则:
考虑到实际问题的意义,还应有x,y∈N*
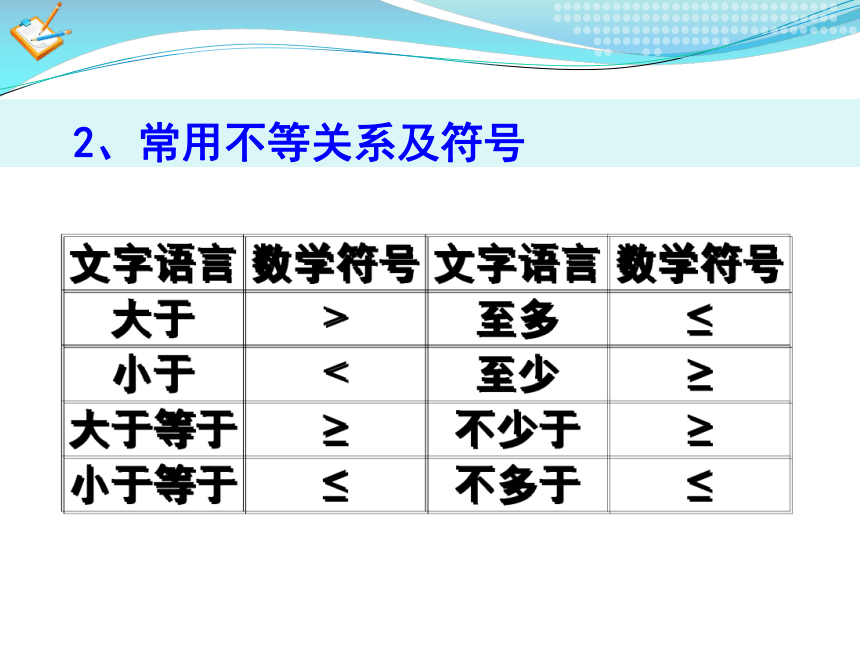
2、常用不等关系及符号
三、不等式基本原理
1、数轴上的任意两点中,右边点对应的实数比左边点对应的实数大。
A(a)
B(b)
x
O
在数轴上,如果表示实数a和b的两个点分别为A和B,则点A和点B在数轴上的位置关系有以下三种:
(1)点A和点B重合;
(2)点A在点B的右侧;
(3)点A在点B的左侧。
a - b < 0 <=> a < b
a - b > 0 <=> a > b
a - b = 0 <=> a = b
在这三种位置关系中,有且仅有一种成立,由此可得到结论:
对于任意两个实数a和b,在a=b,a>b,a1》作差法
.作差比较法的步骤是
★作差;
★变形:配方、因式分解、通分、分母
(分子)有理化等;
★判断符号;
★作出结论.
2》作商法
★对于两个正数a,b,如果a/b >1,那么a > b;如果a/b <1,那么a <b;如果a/b =1,那么a=b。反之也成立,即对于两个正数a,b,有 : a/b >1 a >b; a/b =1 a=b; a/b<1 a<b
★对于两个负数a,b呢?
2、实数比较大小的方法
四、不等式的基本性质
(同向不等式的可加性)
(同向不等式的可乘性)
(可乘方性、可开方性)
1 1
a b
b< a < 0
>
=
<
五、小结:
1.不等关系是普遍存在的
2.用不等式(组)来表示不等关系
3.不等式基本原理
a - b > 0 <=> a > b
a - b = 0 <=> a = b
a - b < 0 <=> a < b
4.不等式的基本性质
谢谢大家,再见!
敬请多提宝贵意见!
欢迎光临
现实世界和日常生活中,既有相等关系,又存在着大量的不等关系.如两点之间线段最短,三角形两边之和大于第三边,等等.人们还经常用长与短、高与矮、轻与重、大与小、不超过或不少于等来描述某种客观事物在数量上存在的不等关系。
课程导入
讲授新课
一、不等关系是普遍存在的
想一想, 举出几个现实生活中与不等关系有关的例子
限速10km/h的路标,指示司机前方路段行驶时,应使汽车的速度v不超过10km/h.表示出不等关系是 。
V≤10
1、不等式定义
用不等号(<、>、≤、≥、≠)表示不等关系的式子叫不等式。用“<”或“>”连接的不等式叫严格不等式,用“≤”或“≥”连接的不等式叫非严格不等式。
二、用不等式(组)来表示不等关系
问题1 设点A与平面的距离为d, B为平面上的任意一点,则可得到不等式.
二、用不等式(组)来表示不等关系
答案:d≤|AB|
问题2 今天的天气预报说:明天早晨最低温度为9℃,明天白天的最高温度为16℃ ,那么明天白天的温度t℃满足什么关系?
答案: 9≤t≤16
二、用不等式(组)来表示不等关系
问题3 某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格。按照生产的要求,600mm的钢管的数量不能超过500mm钢管的3倍。怎样写出满足上述所有不等关系的不等式呢?
分析:设截得500mm的钢管x根,截得600mm的钢管y根,则:
考虑到实际问题的意义,还应有x,y∈N*
2、常用不等关系及符号
三、不等式基本原理
1、数轴上的任意两点中,右边点对应的实数比左边点对应的实数大。
A(a)
B(b)
x
O
在数轴上,如果表示实数a和b的两个点分别为A和B,则点A和点B在数轴上的位置关系有以下三种:
(1)点A和点B重合;
(2)点A在点B的右侧;
(3)点A在点B的左侧。
a - b < 0 <=> a < b
a - b > 0 <=> a > b
a - b = 0 <=> a = b
在这三种位置关系中,有且仅有一种成立,由此可得到结论:
对于任意两个实数a和b,在a=b,a>b,a
.作差比较法的步骤是
★作差;
★变形:配方、因式分解、通分、分母
(分子)有理化等;
★判断符号;
★作出结论.
2》作商法
★对于两个正数a,b,如果a/b >1,那么a > b;如果a/b <1,那么a <b;如果a/b =1,那么a=b。反之也成立,即对于两个正数a,b,有 : a/b >1 a >b; a/b =1 a=b; a/b<1 a<b
★对于两个负数a,b呢?
2、实数比较大小的方法
四、不等式的基本性质
(同向不等式的可加性)
(同向不等式的可乘性)
(可乘方性、可开方性)
1 1
a b
b< a < 0
>
=
<
五、小结:
1.不等关系是普遍存在的
2.用不等式(组)来表示不等关系
3.不等式基本原理
a - b > 0 <=> a > b
a - b = 0 <=> a = b
a - b < 0 <=> a < b
4.不等式的基本性质
谢谢大家,再见!
敬请多提宝贵意见!
