初中数学湘教版九年级上册3.5相似三角形的应用练习题(Word版 含解析)
文档属性
| 名称 | 初中数学湘教版九年级上册3.5相似三角形的应用练习题(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 211.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 22:45:56 | ||
图片预览



文档简介
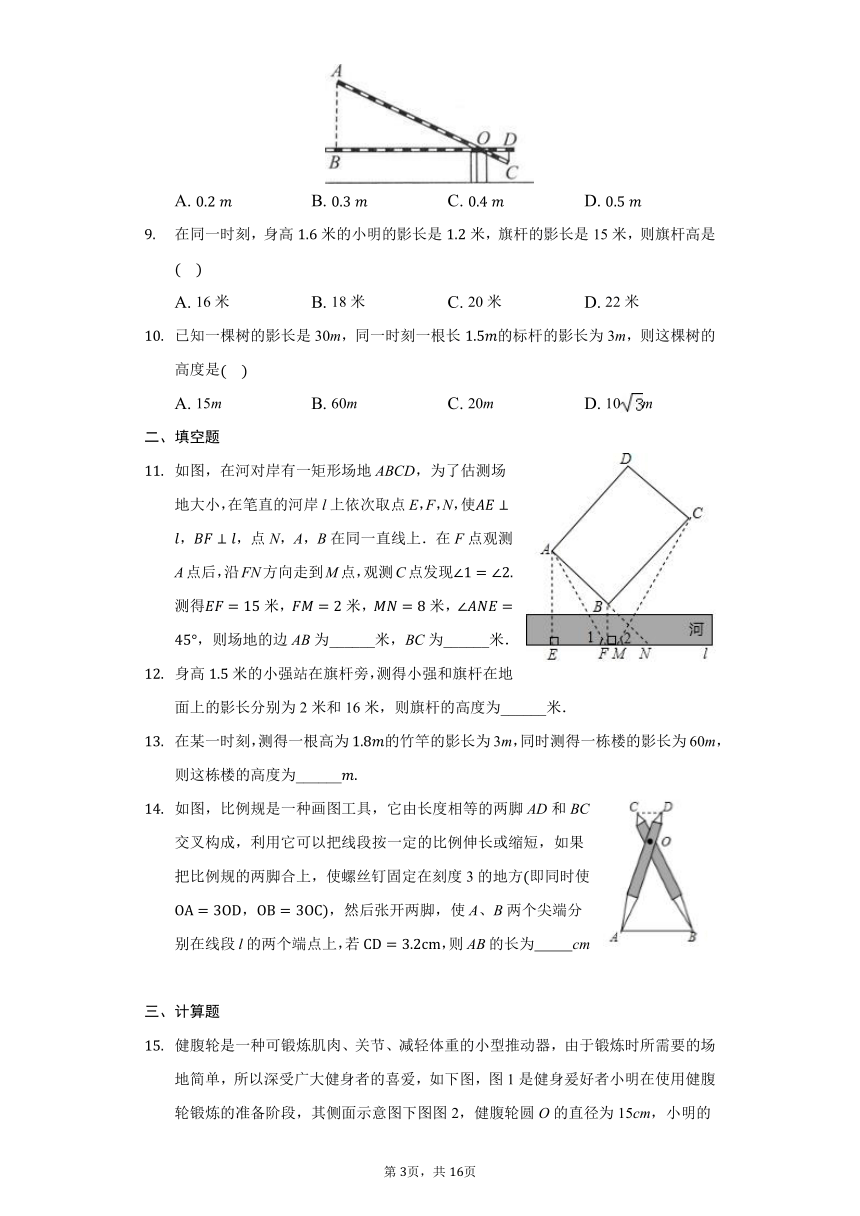
初中数学湘教版九年级上册第三章3.5相似三角形的应用练习题
一、选择题
在如图所示的象棋盘各个小正方形的边长均相等中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似
A.
处
B.
处
C.
处
D.
处
如图是小明利用等腰直角三角板测量旗杆高度的示意图.等腰直角三角板的斜边BD与地面AF平行,当小明的视线恰好沿BC经过旗杆顶部点E时,测量出此时他所在的位置点A与旗杆底部点F的距离为10米.如果小明的眼睛距离地面米,那么旗杆EF的高度为
A.
10米
B.
米
C.
米
D.
米
如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知,,且测得米,米,米,那么该古城墙的高度是
A.
6米
B.
8米
C.
18米
D.
24米
学校门口的栏杆如图所示,栏杆从水平位置BD绕点O旋转到AC位置,已知,,垂足分别为B,D,,,,则栏杆C端应下降的垂直距离CD为
A.
B.
C.
D.
如图,某人拿着一把分度值为厘米的刻度尺,站在距电线杆25m的地方,手臂向前伸直,将刻度尺竖直,看到刻度尺上14cm的长度恰好遮住电线杆.已知臂长为70cm,则电线杆的高是???????????????????????????????????????????????????????????????????
A.
5m
B.
6m
C.
125m
D.
4m
如图所示,利用标杆BE测量建筑物的高度.已知标杆BE高,测得,则建筑物CD的高是
A.
B.
C.
D.
如图,有一块三角形余料ABC,,高线,要把它加工成一个矩形零件,使矩形的一边在BC上,点P,M分别在AB,AC上,若满足PM::2,则PM的长为
A.
60mm
B.
C.
20mm
D.
学校门口的栏杆示意图如图所示,栏杆从水平位置BD绕点O旋转到AC位置,已知,,垂足分别为B,D,,,,则栏杆C端应下降的垂直距离CD为?
?
A.
B.
C.
D.
在同一时刻,身高米的小明的影长是米,旗杆的影长是15米,则旗杆高是
A.
16米
B.
18米
C.
20米
D.
22米
已知一棵树的影长是30m,同一时刻一根长的标杆的影长为3m,则这棵树的高度是
A.
15m
B.
60m
C.
20m
D.
10m
二、填空题
如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使,,点N,A,B在同一直线上.在F点观测A点后,沿FN方向走到M点,观测C点发现测得米,米,米,,则场地的边AB为______米,BC为______米.
身高米的小强站在旗杆旁,测得小强和旗杆在地面上的影长分别为2米和16米,则旗杆的高度为______米.
在某一时刻,测得一根高为的竹竿的影长为3m,同时测得一栋楼的影长为60m,则这栋楼的高度为______
如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短,如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方即同时使,,然后张开两脚,使A、B两个尖端分别在线段l的两个端点上,若,则AB的长为??????????cm.
三、计算题
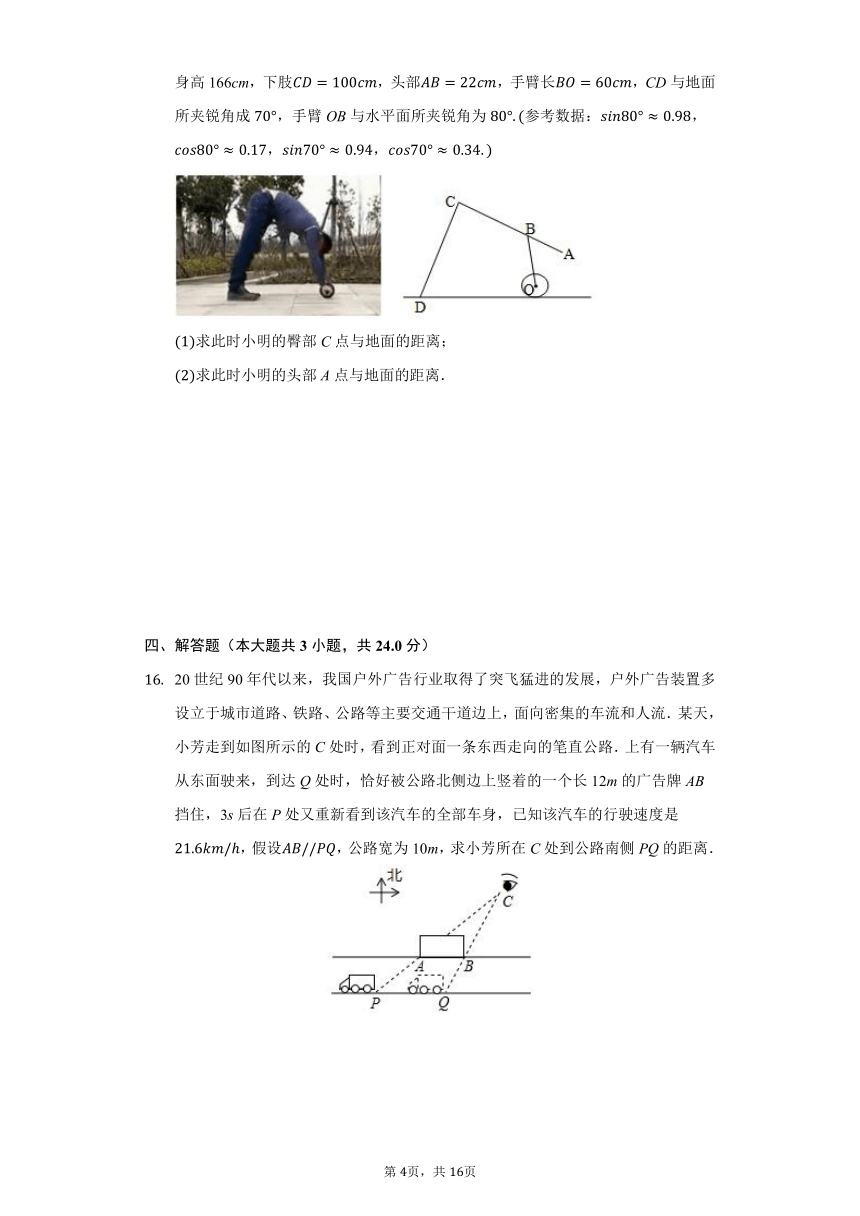
健腹轮是一种可锻炼肌肉、关节、减轻体重的小型推动器,由于锻炼时所需要的场地简单,所以深受广大健身者的喜爱,如下图,图1是健身爰好者小明在使用健腹轮锻炼的准备阶段,其侧面示意图下图图2,健腹轮圆O的直径为15cm,小明的身高166cm,下肢,头部,手臂长,CD与地面所夹锐角成,手臂OB与水平面所夹锐角为参考数据:,,,
求此时小明的臀部C点与地面的距离;
求此时小明的头部A点与地面的距离.
四、解答题(本大题共3小题,共24.0分)
20世纪90年代以来,我国户外广告行业取得了突飞猛进的发展,户外广告装置多设立于城市道路、铁路、公路等主要交通干道边上,面向密集的车流和人流.某天,小芳走到如图所示的C处时,看到正对面一条东西走向的笔直公路.上有一辆汽车从东面驶来,到达Q处时,恰好被公路北侧边上竖着的一个长12m的广告牌AB挡住,3s后在P处又重新看到该汽车的全部车身,已知该汽车的行驶速度是,假设,公路宽为10m,求小芳所在C处到公路南侧PQ的距离.
小明准备利用所学的知识测量旗杆AB的高度.他设计了如下的测量方案:选取一个合适观测点,在地面C处垂直地面竖立高度为2米的标杆CD,小明调整自己的位置到F处,使得视线与D、B在同一直线上,此时测得米,然后小明沿着FC方向前进11米到G处,利用随身携带的等腰直角三角形测得B点的仰角为,已知小明眼睛到地面距离为米米,请你根据题中所给的数据计算旗杆的高度.
西安市的大雁塔又名“慈恩寺塔”,是国家级文物保护单位,玄奘为保存由天竺经丝绸之路带回长安的经卷主持修建了大雁塔,最初五层,后加盖至九层,是西安市的标志性建筑之一,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,大雁塔的塔尖点B正好在同一直线上,测得米,将标杆CD向后平移到点G处,这时地面上的点F,标杆的顶端点H,大雁塔的塔尖点B正好在同一直线上点F,点G,点E,点C与塔底处的点A在同一直线上,这时测得米,米,请你根据以上数据,计算大雁塔的高度AB.
答案和解析
1.【答案】B
【解析】
【分析】
本题考查了相似三角形的知识,解题的关键是利用勾股定理求得三角形的各边的长,难度不大.
确定“帅”、“相”、“兵”所在位置的格点构成的三角形的三边的长,然后利用相似三角形的对应边的比相等确定第三个顶点的位置即可.
【解答】
解:帅”、“相”、“兵”所在位置的格点构成的三角形的三边的长分别为2、、;
“车”、“炮”之间的距离为1,
“炮”之间的距离为,“车”之间的距离为,
,
马应该落在的位置,
故选:B.
2.【答案】B
【解析】解:延长BD交EF于H,如图,
,,
,
易得四边形ABHF为矩形,
,,
为等腰直角三角形,
,
为等腰直角三角形,
,
.
答:旗杆EF的高度为.
故选:B.
延长BD交EF于H,如图,利用四边形ABHF为矩形得到,,再利用为等腰直角三角形,可判断为等腰直角三角形,所以,
然后计算即可.
本题考查了相似三角形的应用:利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.也考查了等腰直角三角形的性质.
3.【答案】B
【解析】
【分析】
本题综合考查了平面镜反射和相似形的知识,是一道较为简单的题,考查相似三角形在测量中的应用.
由已知得∽,则根据相似形的性质可得,解答即可.
【解答】
解:由题意知:光线AP与光线PC,,
∽,
,米.
故选B.
4.【答案】C
【解析】
【分析】
本题主要考查相似三角形的应用,解题的关键是熟练掌握相似三角形的判定与性质由,可证∽,据此得,将已知数据代入即可求解.
【解答】
解:,,
,
又,
∽,
则,
,,,
,
解得:.
故选C.
5.【答案】A
【解析】
【分析】
此题主要考查了相似三角形的应用,利用相似三角形对应高的比等于对应边的比解题是关键.先求出∽,再根据三角形对应高的比等于对应边的比,这样就可以求出电线杆EF的高.
【解答】
解:作于N,交BC于M,
,
于M,
∽,
,
.,,
.
故选:A.
6.【答案】B
【解析】解:,
∽,
,即,
米.
故选:B.
先证明∽,则利用相似三角形的性质得,然后利用比例性质求出CD即可.
本题考查了相似三角形的应用:借助标杆或直尺测量物体的高度.利用杆或直尺测量物体的高度就是利用杆或直尺的高长作为三角形的边,利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.
7.【答案】A
【解析】
【分析】本题考查相似三角形的应用,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型,利用相似三角形的性质构建方程即可解决问题.
【解答】解:,可设,则,
由条件可得APMABC,
,即,解得,
,
故选A.
8.【答案】C
【解析】
【分析】
本题主要考查相似三角形的应用,相似三角形的判定及性质的有关知识,属于中档题.
由、知∽,据此得,将已知数据代入即可得.
【解答】
解:,,
,
又,
∽,
则,
,,,
,
解得:.
故选C.
9.【答案】C
【解析】
【分析】
本题考查了相似三角形的应用,根据相似三角形的对应边的比相等,
【解答】
解:?
设旗杆高是x米
根据题意得,
,
故选C.
10.【答案】A
【解析】
【分析】
本题主要考查的是相似三角形的应用的有关知识,在同一时刻,物体的实际高度和影长成比例,据此列方程即可解答.
【解答】
解:设这棵树的高度为xm,根据在同一时刻同一地点任何物体的高与其影子的比值是相同的得:,
这棵树的高度是15m.
故选:A.
11.【答案】?
【解析】解:,,
,
和是等腰直角三角形,
,,
米,米,米,
米,米,
,,
米;
过C作于H,过B作交AE于P,交CH于Q,
,
四边形PEHQ和四边形PEFB是矩形,
,,,
,,
∽,
,
设,,
,,
,
,
,
∽,
,
,
,
,
,
故答案为:,.
根据已知条件得到和是等腰直角三角形,求得米,米,于是得到米;过C作于H,过B作交AE于P,交CH于Q,根据矩形的性质得到,,,根据相似三角形的性质即可得到结论.
本题考查了相似三角形的应用,矩形的性质,等腰直角三角形的判定和性质,正确的识别图形是解题的关键.
12.【答案】12
【解析】解:设旗杆高度为x米,
根据题意得:,
解得:,
故答案为:12.
根据同一时刻同一地点物高与影长成正比求得答案即可.
本题考查相似三角形性质的应用.解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
13.【答案】36
【解析】解:设这栋楼的高度为hm,
在某一时刻,测得一根高为的竹竿的影长为3m,同时测得一栋楼的影长为60m,
,解得.
故答案为:36.
根据同一时刻物高与影长成正比即可得出结论.
本题考查的是相似三角形的应用,熟知同一时刻物高与影长成正比是解答此题的关键.
14.【答案】
【解析】
【分析】
本题考查相似三角形的应用,解题的关键是熟练掌握相似三角形的判定方法,学会利用相似三角形的性质解决问题,属于中考常考题型.
首先根据题意利用两组对边的比相等且夹角相等的三角形是相似三角形判定相似,然后利用相似三角形的性质求解.
【解答】
解:,,
:::1,,
∽,
,
,
,
,
故答案为.
15.【答案】解:如图,
过C点作于E点
在中
,
此时小明的臀部C点与地面的距离94cm;
过A作于M,
过O作于N
过B作交AM、ON于F、G点
在中
,
,
∽
,
,,
,
,
,
答:小明的头部A点与地面的距离为.
【解析】过C点作于E点,根据三角函数即可求解;
过A作于M,过O作于N过B作交AM、ON于F、G点,可以证明∽,对应边成比例可得,再根据三角函数即可求解.
本题考查了解直角三角形的应用、相似三角形的判定与性质,解决本题的关键是熟练运用三角函数.
16.【答案】解:设小芳所在C处到公路南侧PQ的距离为xm,
,
,
∽,
,
,
,
小芳所在C处到公路南侧PQ的距离为30m.
【解析】通过证明∽可得,可求解.
本题考查了相似三角形的应用,证明∽是本题的关键.
17.【答案】解:如图,延长EH交AB于点N,
由题意得,,,,,,
,
,,
设,
,
∽,
,
,
解得:,
,
答:旗杆的高度为.
【解析】如图,延长EH交AB于点N,设,根据相似三角形的性质列方程即可得到结论.
本题考查了相似三角形的应用,根据相似三角形对应边成比例列出比例式是解题的关键,要注意加上人的视线的高度.
18.【答案】解:∽,∽,
,,
,
,
,
米,
,
,
米,
答:大雁塔的高度AB为55米.
【解析】易知∽,∽,可得,,因为,推出,列出方程求出米,由,可得,由此即可解决问题.
本题考查相似三角形的应用,解题的关键是灵活运用所学知识解决问题,学会构建方程解决问题,属于中考常考题型.
第2页,共2页
第1页,共1页
一、选择题
在如图所示的象棋盘各个小正方形的边长均相等中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似
A.
处
B.
处
C.
处
D.
处
如图是小明利用等腰直角三角板测量旗杆高度的示意图.等腰直角三角板的斜边BD与地面AF平行,当小明的视线恰好沿BC经过旗杆顶部点E时,测量出此时他所在的位置点A与旗杆底部点F的距离为10米.如果小明的眼睛距离地面米,那么旗杆EF的高度为
A.
10米
B.
米
C.
米
D.
米
如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知,,且测得米,米,米,那么该古城墙的高度是
A.
6米
B.
8米
C.
18米
D.
24米
学校门口的栏杆如图所示,栏杆从水平位置BD绕点O旋转到AC位置,已知,,垂足分别为B,D,,,,则栏杆C端应下降的垂直距离CD为
A.
B.
C.
D.
如图,某人拿着一把分度值为厘米的刻度尺,站在距电线杆25m的地方,手臂向前伸直,将刻度尺竖直,看到刻度尺上14cm的长度恰好遮住电线杆.已知臂长为70cm,则电线杆的高是???????????????????????????????????????????????????????????????????
A.
5m
B.
6m
C.
125m
D.
4m
如图所示,利用标杆BE测量建筑物的高度.已知标杆BE高,测得,则建筑物CD的高是
A.
B.
C.
D.
如图,有一块三角形余料ABC,,高线,要把它加工成一个矩形零件,使矩形的一边在BC上,点P,M分别在AB,AC上,若满足PM::2,则PM的长为
A.
60mm
B.
C.
20mm
D.
学校门口的栏杆示意图如图所示,栏杆从水平位置BD绕点O旋转到AC位置,已知,,垂足分别为B,D,,,,则栏杆C端应下降的垂直距离CD为?
?
A.
B.
C.
D.
在同一时刻,身高米的小明的影长是米,旗杆的影长是15米,则旗杆高是
A.
16米
B.
18米
C.
20米
D.
22米
已知一棵树的影长是30m,同一时刻一根长的标杆的影长为3m,则这棵树的高度是
A.
15m
B.
60m
C.
20m
D.
10m
二、填空题
如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使,,点N,A,B在同一直线上.在F点观测A点后,沿FN方向走到M点,观测C点发现测得米,米,米,,则场地的边AB为______米,BC为______米.
身高米的小强站在旗杆旁,测得小强和旗杆在地面上的影长分别为2米和16米,则旗杆的高度为______米.
在某一时刻,测得一根高为的竹竿的影长为3m,同时测得一栋楼的影长为60m,则这栋楼的高度为______
如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短,如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方即同时使,,然后张开两脚,使A、B两个尖端分别在线段l的两个端点上,若,则AB的长为??????????cm.
三、计算题
健腹轮是一种可锻炼肌肉、关节、减轻体重的小型推动器,由于锻炼时所需要的场地简单,所以深受广大健身者的喜爱,如下图,图1是健身爰好者小明在使用健腹轮锻炼的准备阶段,其侧面示意图下图图2,健腹轮圆O的直径为15cm,小明的身高166cm,下肢,头部,手臂长,CD与地面所夹锐角成,手臂OB与水平面所夹锐角为参考数据:,,,
求此时小明的臀部C点与地面的距离;
求此时小明的头部A点与地面的距离.
四、解答题(本大题共3小题,共24.0分)
20世纪90年代以来,我国户外广告行业取得了突飞猛进的发展,户外广告装置多设立于城市道路、铁路、公路等主要交通干道边上,面向密集的车流和人流.某天,小芳走到如图所示的C处时,看到正对面一条东西走向的笔直公路.上有一辆汽车从东面驶来,到达Q处时,恰好被公路北侧边上竖着的一个长12m的广告牌AB挡住,3s后在P处又重新看到该汽车的全部车身,已知该汽车的行驶速度是,假设,公路宽为10m,求小芳所在C处到公路南侧PQ的距离.
小明准备利用所学的知识测量旗杆AB的高度.他设计了如下的测量方案:选取一个合适观测点,在地面C处垂直地面竖立高度为2米的标杆CD,小明调整自己的位置到F处,使得视线与D、B在同一直线上,此时测得米,然后小明沿着FC方向前进11米到G处,利用随身携带的等腰直角三角形测得B点的仰角为,已知小明眼睛到地面距离为米米,请你根据题中所给的数据计算旗杆的高度.
西安市的大雁塔又名“慈恩寺塔”,是国家级文物保护单位,玄奘为保存由天竺经丝绸之路带回长安的经卷主持修建了大雁塔,最初五层,后加盖至九层,是西安市的标志性建筑之一,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,大雁塔的塔尖点B正好在同一直线上,测得米,将标杆CD向后平移到点G处,这时地面上的点F,标杆的顶端点H,大雁塔的塔尖点B正好在同一直线上点F,点G,点E,点C与塔底处的点A在同一直线上,这时测得米,米,请你根据以上数据,计算大雁塔的高度AB.
答案和解析
1.【答案】B
【解析】
【分析】
本题考查了相似三角形的知识,解题的关键是利用勾股定理求得三角形的各边的长,难度不大.
确定“帅”、“相”、“兵”所在位置的格点构成的三角形的三边的长,然后利用相似三角形的对应边的比相等确定第三个顶点的位置即可.
【解答】
解:帅”、“相”、“兵”所在位置的格点构成的三角形的三边的长分别为2、、;
“车”、“炮”之间的距离为1,
“炮”之间的距离为,“车”之间的距离为,
,
马应该落在的位置,
故选:B.
2.【答案】B
【解析】解:延长BD交EF于H,如图,
,,
,
易得四边形ABHF为矩形,
,,
为等腰直角三角形,
,
为等腰直角三角形,
,
.
答:旗杆EF的高度为.
故选:B.
延长BD交EF于H,如图,利用四边形ABHF为矩形得到,,再利用为等腰直角三角形,可判断为等腰直角三角形,所以,
然后计算即可.
本题考查了相似三角形的应用:利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.也考查了等腰直角三角形的性质.
3.【答案】B
【解析】
【分析】
本题综合考查了平面镜反射和相似形的知识,是一道较为简单的题,考查相似三角形在测量中的应用.
由已知得∽,则根据相似形的性质可得,解答即可.
【解答】
解:由题意知:光线AP与光线PC,,
∽,
,米.
故选B.
4.【答案】C
【解析】
【分析】
本题主要考查相似三角形的应用,解题的关键是熟练掌握相似三角形的判定与性质由,可证∽,据此得,将已知数据代入即可求解.
【解答】
解:,,
,
又,
∽,
则,
,,,
,
解得:.
故选C.
5.【答案】A
【解析】
【分析】
此题主要考查了相似三角形的应用,利用相似三角形对应高的比等于对应边的比解题是关键.先求出∽,再根据三角形对应高的比等于对应边的比,这样就可以求出电线杆EF的高.
【解答】
解:作于N,交BC于M,
,
于M,
∽,
,
.,,
.
故选:A.
6.【答案】B
【解析】解:,
∽,
,即,
米.
故选:B.
先证明∽,则利用相似三角形的性质得,然后利用比例性质求出CD即可.
本题考查了相似三角形的应用:借助标杆或直尺测量物体的高度.利用杆或直尺测量物体的高度就是利用杆或直尺的高长作为三角形的边,利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.
7.【答案】A
【解析】
【分析】本题考查相似三角形的应用,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型,利用相似三角形的性质构建方程即可解决问题.
【解答】解:,可设,则,
由条件可得APMABC,
,即,解得,
,
故选A.
8.【答案】C
【解析】
【分析】
本题主要考查相似三角形的应用,相似三角形的判定及性质的有关知识,属于中档题.
由、知∽,据此得,将已知数据代入即可得.
【解答】
解:,,
,
又,
∽,
则,
,,,
,
解得:.
故选C.
9.【答案】C
【解析】
【分析】
本题考查了相似三角形的应用,根据相似三角形的对应边的比相等,
【解答】
解:?
设旗杆高是x米
根据题意得,
,
故选C.
10.【答案】A
【解析】
【分析】
本题主要考查的是相似三角形的应用的有关知识,在同一时刻,物体的实际高度和影长成比例,据此列方程即可解答.
【解答】
解:设这棵树的高度为xm,根据在同一时刻同一地点任何物体的高与其影子的比值是相同的得:,
这棵树的高度是15m.
故选:A.
11.【答案】?
【解析】解:,,
,
和是等腰直角三角形,
,,
米,米,米,
米,米,
,,
米;
过C作于H,过B作交AE于P,交CH于Q,
,
四边形PEHQ和四边形PEFB是矩形,
,,,
,,
∽,
,
设,,
,,
,
,
,
∽,
,
,
,
,
,
故答案为:,.
根据已知条件得到和是等腰直角三角形,求得米,米,于是得到米;过C作于H,过B作交AE于P,交CH于Q,根据矩形的性质得到,,,根据相似三角形的性质即可得到结论.
本题考查了相似三角形的应用,矩形的性质,等腰直角三角形的判定和性质,正确的识别图形是解题的关键.
12.【答案】12
【解析】解:设旗杆高度为x米,
根据题意得:,
解得:,
故答案为:12.
根据同一时刻同一地点物高与影长成正比求得答案即可.
本题考查相似三角形性质的应用.解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
13.【答案】36
【解析】解:设这栋楼的高度为hm,
在某一时刻,测得一根高为的竹竿的影长为3m,同时测得一栋楼的影长为60m,
,解得.
故答案为:36.
根据同一时刻物高与影长成正比即可得出结论.
本题考查的是相似三角形的应用,熟知同一时刻物高与影长成正比是解答此题的关键.
14.【答案】
【解析】
【分析】
本题考查相似三角形的应用,解题的关键是熟练掌握相似三角形的判定方法,学会利用相似三角形的性质解决问题,属于中考常考题型.
首先根据题意利用两组对边的比相等且夹角相等的三角形是相似三角形判定相似,然后利用相似三角形的性质求解.
【解答】
解:,,
:::1,,
∽,
,
,
,
,
故答案为.
15.【答案】解:如图,
过C点作于E点
在中
,
此时小明的臀部C点与地面的距离94cm;
过A作于M,
过O作于N
过B作交AM、ON于F、G点
在中
,
,
∽
,
,,
,
,
,
答:小明的头部A点与地面的距离为.
【解析】过C点作于E点,根据三角函数即可求解;
过A作于M,过O作于N过B作交AM、ON于F、G点,可以证明∽,对应边成比例可得,再根据三角函数即可求解.
本题考查了解直角三角形的应用、相似三角形的判定与性质,解决本题的关键是熟练运用三角函数.
16.【答案】解:设小芳所在C处到公路南侧PQ的距离为xm,
,
,
∽,
,
,
,
小芳所在C处到公路南侧PQ的距离为30m.
【解析】通过证明∽可得,可求解.
本题考查了相似三角形的应用,证明∽是本题的关键.
17.【答案】解:如图,延长EH交AB于点N,
由题意得,,,,,,
,
,,
设,
,
∽,
,
,
解得:,
,
答:旗杆的高度为.
【解析】如图,延长EH交AB于点N,设,根据相似三角形的性质列方程即可得到结论.
本题考查了相似三角形的应用,根据相似三角形对应边成比例列出比例式是解题的关键,要注意加上人的视线的高度.
18.【答案】解:∽,∽,
,,
,
,
,
米,
,
,
米,
答:大雁塔的高度AB为55米.
【解析】易知∽,∽,可得,,因为,推出,列出方程求出米,由,可得,由此即可解决问题.
本题考查相似三角形的应用,解题的关键是灵活运用所学知识解决问题,学会构建方程解决问题,属于中考常考题型.
第2页,共2页
第1页,共1页
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
