人教版数学六年级上册第四单元第2课时 比的基本性质 课件(28张ppt)
文档属性
| 名称 | 人教版数学六年级上册第四单元第2课时 比的基本性质 课件(28张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 22:59:55 | ||
图片预览






文档简介
六年级数学上册(RJ)教学课件
第四单元 比
第2课时 比的基本性质
目录
CONTENTS
情景导入
01
学习目标
02
探究与发现
03
学以致用
04
课后作业
06
课堂小结
05
情景导学
第一部分
情景导学
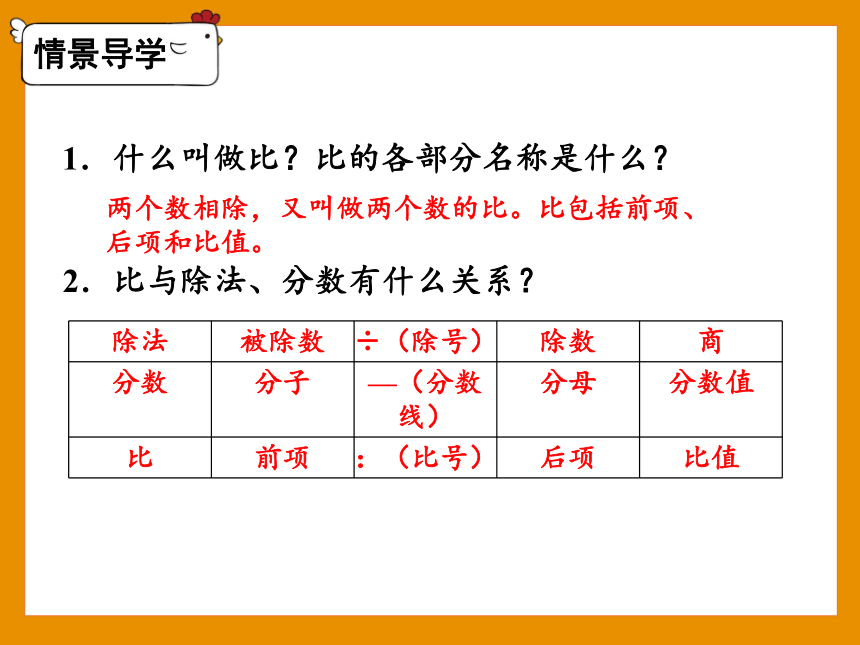
两个数相除,又叫做两个数的比。比包括前项、后项和比值。
1.什么叫做比?比的各部分名称是什么?
2.比与除法、分数有什么关系?
{5940675A-B579-460E-94D1-54222C63F5DA}除法
被除数
÷(除号)
除数
商
分数
分子
—(分数线)
分母
分数值
比
前项
:(比号)
后项
比值
第二部分
学习目标
学习目标
1. 掌握比的基本性质,能根据比的基本性质化简比。
2.练习商不变的性质和分数的基本性质迁移到比的基本性质。
第三部分
探究与发现
探索与发现
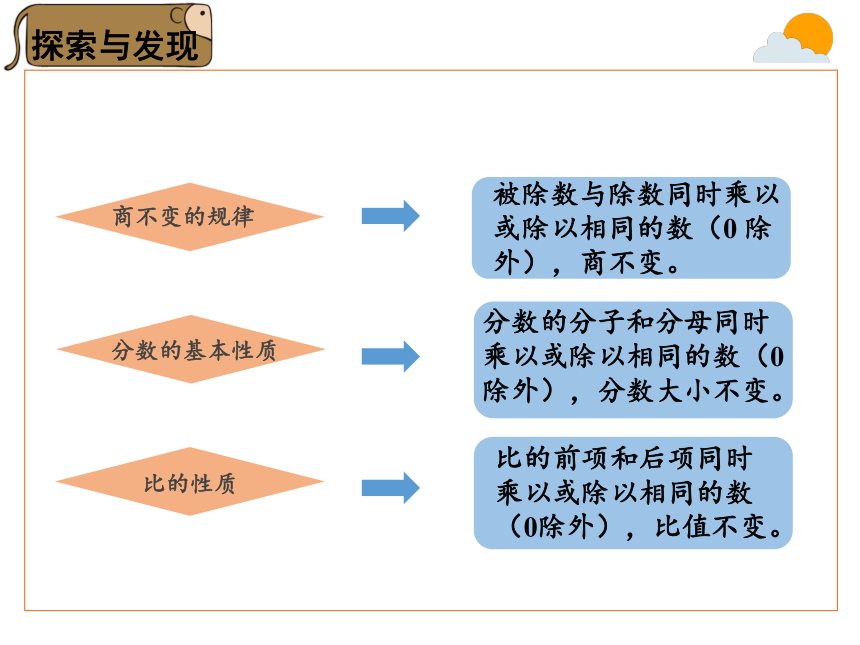
商不变的规律
被除数与除数同时乘以或除以相同的数(0 除外),商不变。
分数的基本性质
分数的分子和分母同时乘以或除以相同的数(0除外),分数大小不变。
比的性质
比的前项和后项同时乘以或除以相同的数(0除外),比值不变。
探索与发现
1 . 为什么在比中要同时乘以或除以相同的数不能是0?
请思考:
【解析】因为如果乘以0,比的后项就变成了0,没有意义。且0不能作除数,更不能同时除以0。
2 . 比的基本性质有什么样的用途?
【解析】利用比的基本性质,我们可以把比化成最简单的整数比,最简整数比的前项和后项是互质数。
探索与发现
被除数和除数同时乘以或者除以相同的数(零除外),商不变。
除法中的商不变规律是什么?
举例:6÷8=(6×2)÷(8×2)=12÷16?
探索与发现
(1)通过比较的过程你有什么发现?
(2)这三个比中有什么规律?
6︰8=6÷8= =
3︰4=3÷4=
12︰16=12÷16= =
8
6
4
3
4
3
16
12
4
3
探索与发现
6÷8=(6×2)÷(8×2)=12÷16
6÷8=(6÷2)÷(8÷2)=3÷4
6:8
6:8
=(6×2):(8×2)
=12:16
=(6÷2):(8÷2)
=3:4
比中有什么样的规律?请你借助学过的知识独立进行研究。
比的前项和后项同时乘或除以相同的数(0除外),比值不变,这叫做比的基本性质。
探索与发现
根据比的基本性质,可以把比化成最简单的整数比。
哪些是整数比?哪些比的前项和后项是互质的?
前项和后项都是整数,而且又互质,这样的比就叫最简单整数比。
18:27 4:9 3:15
4.5:9 5:6 7:11
4:9
5:6
7:11
探索与发现
“神州”五号搭载了两面联合国旗,一面长15cm,宽10cm,另一面长180cm,宽120cm。这两面联合国旗长和宽的最简单的整数比分别是多少?
15 : 10 = (15÷5):(10÷5)= 3:2
180 : 120 = (180÷60):(120÷60)= 3:2
【解析】“15 :10 ”和“180 :120”的前项和后项都是整数,要化最简整数比,就要将前、后项同时除以它们最大的公约数。
15cm
10cm
180cm
120cm
探索与发现
例1:(2)把下面各比化成最简单的整数比。
6
1
9
2
︰
0.75:2
6
1
9
2
︰
=( ×18)︰
6
1
( ×18) =3:4
9
2
化简分数比时:先将前项和后项化成整数比,然后再进行化简。
化简分数比
探索与发现
例1:(2)把下面各比化成最简单的整数比。
6
1
9
2
︰
0.75:2
化简小数比
0.75:2=(0.75×100)︰(2×100)=75:200=3:8
化简小数比时:先将前项和后项化成整数比,然后再进行化简。
探索与发现
6
1
9
2
︰
=( ×18)︰
6
1
( ×18) =3:4
9
2
0.75:2=(0.75×100)︰(2×100)=75:200=3:8
小结:当一个比的前项和后项不是整数时,怎样把它化成最简单整数比?
先把比转化成整数比,然后按照化简整数比的方法化简。
第四部分
学以致用
学以致用
×
×
6:7=(6×0):(7×0)=0
1:2=(1+2):(2+2)=0.75
比的前项和后项不能乘0.
比的前项和后项同时乘或者除以非0的数.
学以致用
把下面各比化成最简单的整数比。
32:16
=(32÷16): (16÷16)=2:1
48:40
=(48÷8): (40÷8)=6:5
0.15:0.3
6
5
6
1
︰
8
3
︰
12
7
8
5
0.125︰
=(0.15×100):(0.3×100)=15︰30=1:2
=( ×6)︰
6
5
( ×6)=5:1
6
1
=( ×24)︰
12
7
( ×24)=14:9
8
3
=(0.125×1000)︰
( ×1000)=125:625=1:5
8
5
学以致用
填空。
(1)2:4的比值是( )。
(2)12:4=( ):8=( ):2=3:( )。
(3)相同时间内,钟表上时针转动圈数与分针转动圈数的比是( )。
(4)2:5中,前项加上4,要使比值不变,后项加上( ),变成( )。
(5)两个正方形的边长是1:2,这两个正方形的面积比是( )。
0.5
24
6
1
1:12
10
15
1:4
学以致用
选择。
(1)比的( )不能为0?
A. 前项 B. 后项 C. 比值 D. 前项或后项
(2)比的前项和后项都除以2,比值( )。
A. 变大 B. 变小 C. 不变 D. 无法确定
(3)在8:10中,如果前项增加8,要使比值不变,后项( )。
A. 增加8 B. 增加16 C. 增加10 D. 不变
B
C
C
学以致用
问题:1. 你听说过“黄金比”吗?
4. 你还了解生活中的黄金比吗?课下查阅相关的资料。
把一条线段分成两部分,如果较短部分与较长部分长度之比等于较长部分与整体长度之比,我们把这个比称为黄金比(约为 0.618︰1)。当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
3. 找一找除了a︰b之外还有其他线段长度符合黄金比吗?
2. 出示图片欣赏,介绍黄金比。
c
c
(c和a也符合黄金比)
第五部分
课堂小结
知识小结
2. 验证方法:① 根据分数、比、除法的关系验证;② 根据比值验证。
1. 比的基本性质:比的前项和后项同时乘以或者同时除以相同的数(0除外),比值不变。
3. 化简比:① 整数比:同时乘以或除以相同的数;② 分数比:前项除以后项;③小数比:先同时扩大化为整数。
第六部分
课后作业
完成同步练习。
课后作业
谢谢观看
下课!
第四单元 比
第2课时 比的基本性质
目录
CONTENTS
情景导入
01
学习目标
02
探究与发现
03
学以致用
04
课后作业
06
课堂小结
05
情景导学
第一部分
情景导学
两个数相除,又叫做两个数的比。比包括前项、后项和比值。
1.什么叫做比?比的各部分名称是什么?
2.比与除法、分数有什么关系?
{5940675A-B579-460E-94D1-54222C63F5DA}除法
被除数
÷(除号)
除数
商
分数
分子
—(分数线)
分母
分数值
比
前项
:(比号)
后项
比值
第二部分
学习目标
学习目标
1. 掌握比的基本性质,能根据比的基本性质化简比。
2.练习商不变的性质和分数的基本性质迁移到比的基本性质。
第三部分
探究与发现
探索与发现
商不变的规律
被除数与除数同时乘以或除以相同的数(0 除外),商不变。
分数的基本性质
分数的分子和分母同时乘以或除以相同的数(0除外),分数大小不变。
比的性质
比的前项和后项同时乘以或除以相同的数(0除外),比值不变。
探索与发现
1 . 为什么在比中要同时乘以或除以相同的数不能是0?
请思考:
【解析】因为如果乘以0,比的后项就变成了0,没有意义。且0不能作除数,更不能同时除以0。
2 . 比的基本性质有什么样的用途?
【解析】利用比的基本性质,我们可以把比化成最简单的整数比,最简整数比的前项和后项是互质数。
探索与发现
被除数和除数同时乘以或者除以相同的数(零除外),商不变。
除法中的商不变规律是什么?
举例:6÷8=(6×2)÷(8×2)=12÷16?
探索与发现
(1)通过比较的过程你有什么发现?
(2)这三个比中有什么规律?
6︰8=6÷8= =
3︰4=3÷4=
12︰16=12÷16= =
8
6
4
3
4
3
16
12
4
3
探索与发现
6÷8=(6×2)÷(8×2)=12÷16
6÷8=(6÷2)÷(8÷2)=3÷4
6:8
6:8
=(6×2):(8×2)
=12:16
=(6÷2):(8÷2)
=3:4
比中有什么样的规律?请你借助学过的知识独立进行研究。
比的前项和后项同时乘或除以相同的数(0除外),比值不变,这叫做比的基本性质。
探索与发现
根据比的基本性质,可以把比化成最简单的整数比。
哪些是整数比?哪些比的前项和后项是互质的?
前项和后项都是整数,而且又互质,这样的比就叫最简单整数比。
18:27 4:9 3:15
4.5:9 5:6 7:11
4:9
5:6
7:11
探索与发现
“神州”五号搭载了两面联合国旗,一面长15cm,宽10cm,另一面长180cm,宽120cm。这两面联合国旗长和宽的最简单的整数比分别是多少?
15 : 10 = (15÷5):(10÷5)= 3:2
180 : 120 = (180÷60):(120÷60)= 3:2
【解析】“15 :10 ”和“180 :120”的前项和后项都是整数,要化最简整数比,就要将前、后项同时除以它们最大的公约数。
15cm
10cm
180cm
120cm
探索与发现
例1:(2)把下面各比化成最简单的整数比。
6
1
9
2
︰
0.75:2
6
1
9
2
︰
=( ×18)︰
6
1
( ×18) =3:4
9
2
化简分数比时:先将前项和后项化成整数比,然后再进行化简。
化简分数比
探索与发现
例1:(2)把下面各比化成最简单的整数比。
6
1
9
2
︰
0.75:2
化简小数比
0.75:2=(0.75×100)︰(2×100)=75:200=3:8
化简小数比时:先将前项和后项化成整数比,然后再进行化简。
探索与发现
6
1
9
2
︰
=( ×18)︰
6
1
( ×18) =3:4
9
2
0.75:2=(0.75×100)︰(2×100)=75:200=3:8
小结:当一个比的前项和后项不是整数时,怎样把它化成最简单整数比?
先把比转化成整数比,然后按照化简整数比的方法化简。
第四部分
学以致用
学以致用
×
×
6:7=(6×0):(7×0)=0
1:2=(1+2):(2+2)=0.75
比的前项和后项不能乘0.
比的前项和后项同时乘或者除以非0的数.
学以致用
把下面各比化成最简单的整数比。
32:16
=(32÷16): (16÷16)=2:1
48:40
=(48÷8): (40÷8)=6:5
0.15:0.3
6
5
6
1
︰
8
3
︰
12
7
8
5
0.125︰
=(0.15×100):(0.3×100)=15︰30=1:2
=( ×6)︰
6
5
( ×6)=5:1
6
1
=( ×24)︰
12
7
( ×24)=14:9
8
3
=(0.125×1000)︰
( ×1000)=125:625=1:5
8
5
学以致用
填空。
(1)2:4的比值是( )。
(2)12:4=( ):8=( ):2=3:( )。
(3)相同时间内,钟表上时针转动圈数与分针转动圈数的比是( )。
(4)2:5中,前项加上4,要使比值不变,后项加上( ),变成( )。
(5)两个正方形的边长是1:2,这两个正方形的面积比是( )。
0.5
24
6
1
1:12
10
15
1:4
学以致用
选择。
(1)比的( )不能为0?
A. 前项 B. 后项 C. 比值 D. 前项或后项
(2)比的前项和后项都除以2,比值( )。
A. 变大 B. 变小 C. 不变 D. 无法确定
(3)在8:10中,如果前项增加8,要使比值不变,后项( )。
A. 增加8 B. 增加16 C. 增加10 D. 不变
B
C
C
学以致用
问题:1. 你听说过“黄金比”吗?
4. 你还了解生活中的黄金比吗?课下查阅相关的资料。
把一条线段分成两部分,如果较短部分与较长部分长度之比等于较长部分与整体长度之比,我们把这个比称为黄金比(约为 0.618︰1)。当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
3. 找一找除了a︰b之外还有其他线段长度符合黄金比吗?
2. 出示图片欣赏,介绍黄金比。
c
c
(c和a也符合黄金比)
第五部分
课堂小结
知识小结
2. 验证方法:① 根据分数、比、除法的关系验证;② 根据比值验证。
1. 比的基本性质:比的前项和后项同时乘以或者同时除以相同的数(0除外),比值不变。
3. 化简比:① 整数比:同时乘以或除以相同的数;② 分数比:前项除以后项;③小数比:先同时扩大化为整数。
第六部分
课后作业
完成同步练习。
课后作业
谢谢观看
下课!
