人教版数学六年级上册第五单元第2课时 圆的周长 课件(34张ppt)
文档属性
| 名称 | 人教版数学六年级上册第五单元第2课时 圆的周长 课件(34张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 23:07:23 | ||
图片预览







文档简介
六年级数学上册(RJ)教学课件
第五单元 圆
第2课时 圆的周长
目录
CONTENTS
情景导入
01
学习目标
02
探究与发现
03
学以致用
04
课后作业
06
课堂小结
05
情景导学
第一部分
情景导学
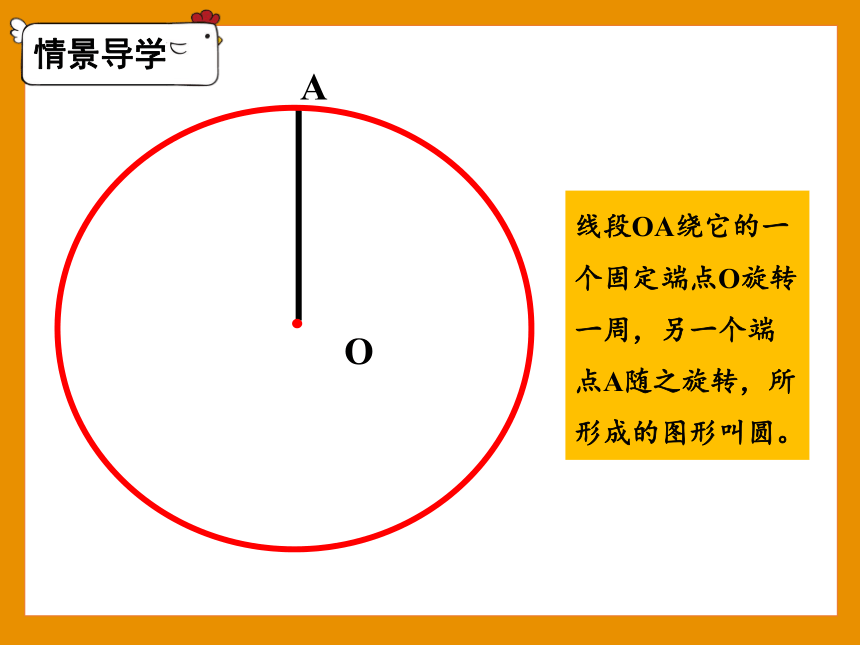
线段OA绕它的一个固定端点O旋转一周,另一个端点A随之旋转,所形成的图形叫圆。
O
A
第二部分
学习目标
学习目标
1.经历探究过程,理解圆的周长和圆周率的关系。
2.理解并掌握圆的周长公式,能利用圆的周长公式解决简单的问题。
3.培养学生逻辑推理能力。
第三部分
探究与发现
探索与发现
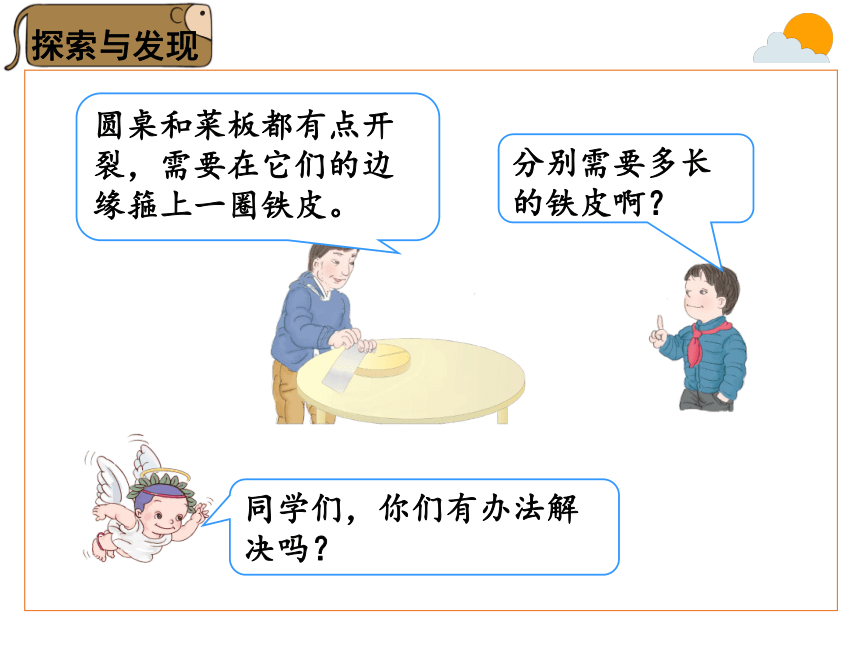
圆桌和菜板都有点开裂,需要在它们的边缘箍上一圈铁皮。
分别需要多长的铁皮啊?
同学们,你们有办法解决吗?
探索与发现
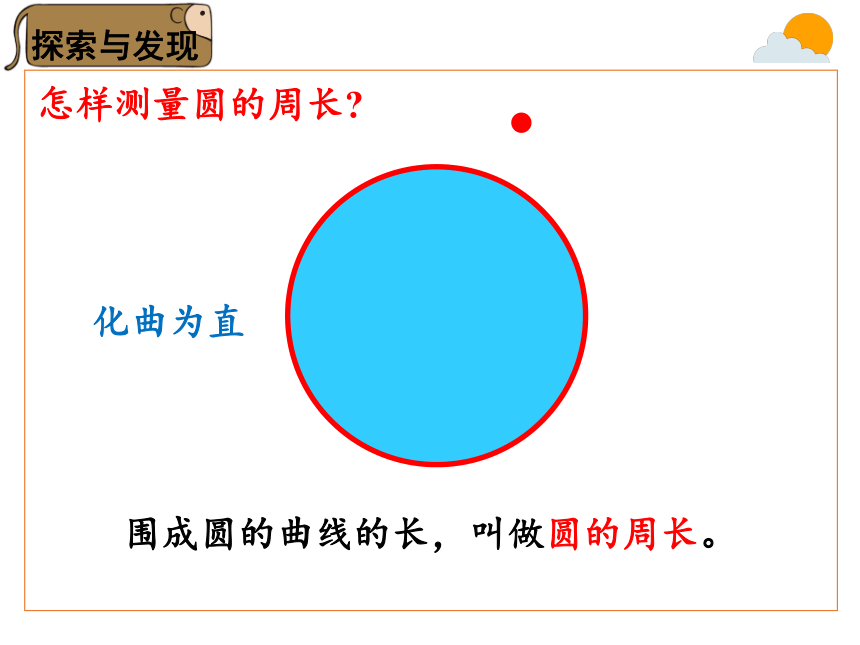
围成圆的曲线的长,叫做圆的周长。
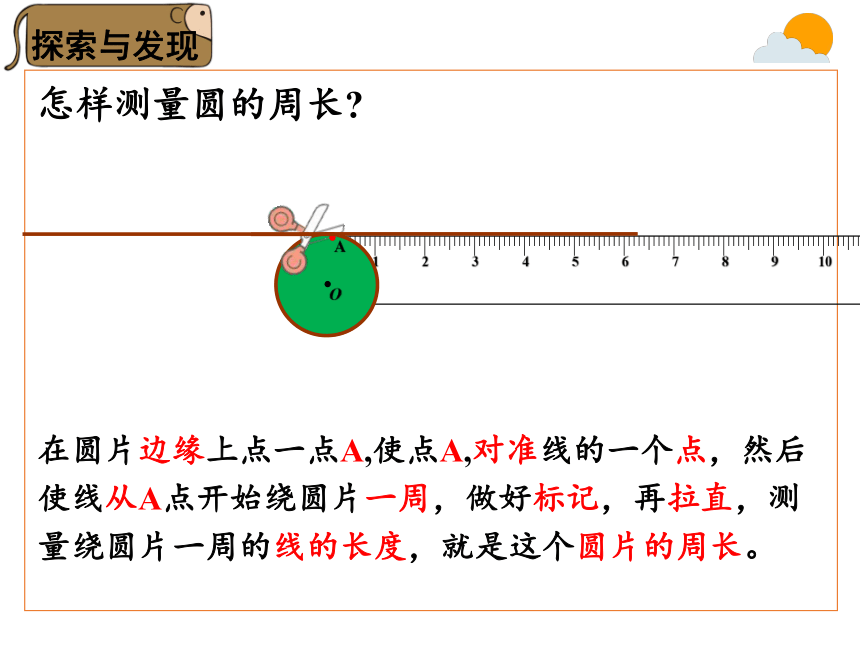
怎样测量圆的周长?
化曲为直
探索与发现
探索与发现
怎样测量圆的周长?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0cm
圆片向右滚动一周,量它的长度。
3厘米
滚动法
探索与发现
在圆片边缘上点一点A,使点A,对准线的一个点,然后使线从A点开始绕圆片一周,做好标记,再拉直,测量绕圆片一周的线的长度,就是这个圆片的周长。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0cm
O
A
怎样测量圆的周长?
探索与发现
像这样,围成圆的曲线的长是圆的周长。除了上面的方法,还可以怎样求圆的周长呢?
圆的周长和圆的大小有关系,圆的大小取决于圆的半径……
探索与发现
让我们来做一个实验:找一些圆形的物品,分别量出它们的周长和直径,并算出周长和直径的比值,把结果填入下表中,看看有什么发现。
原来一个圆的周长总是它的直径的3倍多一些。
物品名称
周长
直径
(保留两位小数)
直径
周长
的比值
茶杯盖
28.3cm
9cm
3.14
光盘
37.85cm
12cm
3.15
硬币
7.85cm
2.5cm
3.14
玩具车车轮
23.5cm
7.5cm
3.13
探索与发现
圆的周长除以直径的商是一个固定的数。我们把它叫做圆周率,用字母π表示。
π=3.141592653……
圆周率
π≈3.14
探索与发现
如果用C表示圆的周长,就有:
C =πd 或 C=2πr
其实,早就有人研究了周长与直径的关系,发现任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率,用字母π表示。它是一个无限不循环小数,π=3.1415926535……但在实际应用中常常只取它的近似值,例如π≈3.14。
探索与发现
这辆自行车后轮转一圈,大约可以走多远?小明家离学校1km,后轮转480圈够吗?
这辆自行车后轮轮胎的半径大约是33cm。
探索与发现
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}已知条件
(1)自行车轮子的半径大约是33cm
(2)小明家离学校1km
所求问题
(1)自行车轮子转1圈,大约可以走多远
(2)小明家到学校,轮子大约转多少圈
信息提取
探索与发现
规范解答
C =2πr
2×3.14×33=207.24(cm)≈2(m)
1km=1000m
1000÷2=500(圈)
答:这辆自行车轮子转1圈,大约可以走2m。骑车从家到学校,轮子大约转了500圈。
本题所求的问题有两个,问题(1)实际就是求轮子的周长,已知半径求周长,应用公式C=2πr 直接计算,注意计算结果要保留整米数。问题(2)是在问题(1)的基础上提出来的,1km的单位名称与问题(1)中的单位名称“米”不统一,应先进行单位换算。
探索与发现
当已知圆的半径,求
圆的周长时,可以用
公式:C=2πr计算 。
求需要转的圈数时:
圈数=距离÷轮子的周长。
第四部分
学以致用
学以致用
(1)圆的周长是直径的( )
A 3.14159倍; B 3.14倍; C 3倍; D π倍
(2)圆的半径扩大为原来的3倍,( )
A 周长扩大为原来的9倍 B 周长扩大为原来的6倍
C 周长扩大为原来的3倍 D 周长不变
D
C
选择题。
学以致用
2×3.14×3
=18.84(cm)
3.14×6
=18.84(cm)
2×3.14×5
=31.4(cm)
求下面各圆的周长。
学以致用
4.71÷3.14=1.5(m)
答:这个圆桌面的直径是1.5 m。
这个圆桌面的直径是多少?
我用卷尺量得圆桌面的周长是4.71 m。
学以致用
有一根长12.56厘米的铁丝,如果把它围成一个正方形,这个正方形的边长是多少厘米?如果把它围成一个圆,这个圆的直径是多少厘米?
分析:
(1)逆推:因为12.66=边长×4
所以 长方形的边长=12.56÷4 =3.14(厘米)
(2)因为12.56=πd
所以圆的 直径=12.56÷3.14=4(厘米)
学以致用
有一根长12.56厘米的铁丝,如果把它围成一个正方形,这个正方形的边长是多少厘米?如果把它围成一个圆,这个圆的直径是多少厘米?
解答:
12.56÷4 =3.14(厘米)
12.56÷3.14=4(厘米)
答:正方形的变长是3.14厘米,圆的直径是4厘米。
1.已知圆的周长,怎样求直径?
2.已知圆的周长,怎样求半径?
d=C÷π
r=C÷2π
学以致用
我国最高的摩天轮—“南昌之星”,转盘直径为153 m,坐着它转动一周,在空中转过的米数是多少?
C=πd
=3.14×153=480.42(m)
答:在空中转过的米数是480.42 m。
学以致用
一个铁环直径是60厘米,从操场东端滚到西端转了90圈,另一个铁环的直径是40厘米,它从东端滚到西端要转多少圈?
【答案】
(3.14×60×90)÷(3.14×40)
=16956÷125.6
=135(圈)
答:直径为40厘米的铁环从东端滚到西端要转135圈。
【解析】根据题意,可利用圆的周长公式分别计算出两个铁环的周长,然后再用第一个铁环的周长乘90就是操场从东到西的长度,再用操场从东到西的长度除以第二个铁环的周长就是第二个铁环转动的圈数,列式解答即可得到答案。
学以致用
第五部分
课堂小结
知识小结
当已知圆的半径,求圆的周长时,可以用
公式:C=2πr计算 。
根据圆的周长求出圆的直径或半径。
利用圆的周长的计算方法可以解决很多问题。通过联系,可以体会到数学知识与日常生活的密切关系,可以感受到数学知识的价值。
第六部分
课后作业
完成》同步练习。
课后作业
谢谢观看
下课!
第五单元 圆
第2课时 圆的周长
目录
CONTENTS
情景导入
01
学习目标
02
探究与发现
03
学以致用
04
课后作业
06
课堂小结
05
情景导学
第一部分
情景导学
线段OA绕它的一个固定端点O旋转一周,另一个端点A随之旋转,所形成的图形叫圆。
O
A
第二部分
学习目标
学习目标
1.经历探究过程,理解圆的周长和圆周率的关系。
2.理解并掌握圆的周长公式,能利用圆的周长公式解决简单的问题。
3.培养学生逻辑推理能力。
第三部分
探究与发现
探索与发现
圆桌和菜板都有点开裂,需要在它们的边缘箍上一圈铁皮。
分别需要多长的铁皮啊?
同学们,你们有办法解决吗?
探索与发现
围成圆的曲线的长,叫做圆的周长。
怎样测量圆的周长?
化曲为直
探索与发现
探索与发现
怎样测量圆的周长?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0cm
圆片向右滚动一周,量它的长度。
3厘米
滚动法
探索与发现
在圆片边缘上点一点A,使点A,对准线的一个点,然后使线从A点开始绕圆片一周,做好标记,再拉直,测量绕圆片一周的线的长度,就是这个圆片的周长。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0cm
O
A
怎样测量圆的周长?
探索与发现
像这样,围成圆的曲线的长是圆的周长。除了上面的方法,还可以怎样求圆的周长呢?
圆的周长和圆的大小有关系,圆的大小取决于圆的半径……
探索与发现
让我们来做一个实验:找一些圆形的物品,分别量出它们的周长和直径,并算出周长和直径的比值,把结果填入下表中,看看有什么发现。
原来一个圆的周长总是它的直径的3倍多一些。
物品名称
周长
直径
(保留两位小数)
直径
周长
的比值
茶杯盖
28.3cm
9cm
3.14
光盘
37.85cm
12cm
3.15
硬币
7.85cm
2.5cm
3.14
玩具车车轮
23.5cm
7.5cm
3.13
探索与发现
圆的周长除以直径的商是一个固定的数。我们把它叫做圆周率,用字母π表示。
π=3.141592653……
圆周率
π≈3.14
探索与发现
如果用C表示圆的周长,就有:
C =πd 或 C=2πr
其实,早就有人研究了周长与直径的关系,发现任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率,用字母π表示。它是一个无限不循环小数,π=3.1415926535……但在实际应用中常常只取它的近似值,例如π≈3.14。
探索与发现
这辆自行车后轮转一圈,大约可以走多远?小明家离学校1km,后轮转480圈够吗?
这辆自行车后轮轮胎的半径大约是33cm。
探索与发现
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}已知条件
(1)自行车轮子的半径大约是33cm
(2)小明家离学校1km
所求问题
(1)自行车轮子转1圈,大约可以走多远
(2)小明家到学校,轮子大约转多少圈
信息提取
探索与发现
规范解答
C =2πr
2×3.14×33=207.24(cm)≈2(m)
1km=1000m
1000÷2=500(圈)
答:这辆自行车轮子转1圈,大约可以走2m。骑车从家到学校,轮子大约转了500圈。
本题所求的问题有两个,问题(1)实际就是求轮子的周长,已知半径求周长,应用公式C=2πr 直接计算,注意计算结果要保留整米数。问题(2)是在问题(1)的基础上提出来的,1km的单位名称与问题(1)中的单位名称“米”不统一,应先进行单位换算。
探索与发现
当已知圆的半径,求
圆的周长时,可以用
公式:C=2πr计算 。
求需要转的圈数时:
圈数=距离÷轮子的周长。
第四部分
学以致用
学以致用
(1)圆的周长是直径的( )
A 3.14159倍; B 3.14倍; C 3倍; D π倍
(2)圆的半径扩大为原来的3倍,( )
A 周长扩大为原来的9倍 B 周长扩大为原来的6倍
C 周长扩大为原来的3倍 D 周长不变
D
C
选择题。
学以致用
2×3.14×3
=18.84(cm)
3.14×6
=18.84(cm)
2×3.14×5
=31.4(cm)
求下面各圆的周长。
学以致用
4.71÷3.14=1.5(m)
答:这个圆桌面的直径是1.5 m。
这个圆桌面的直径是多少?
我用卷尺量得圆桌面的周长是4.71 m。
学以致用
有一根长12.56厘米的铁丝,如果把它围成一个正方形,这个正方形的边长是多少厘米?如果把它围成一个圆,这个圆的直径是多少厘米?
分析:
(1)逆推:因为12.66=边长×4
所以 长方形的边长=12.56÷4 =3.14(厘米)
(2)因为12.56=πd
所以圆的 直径=12.56÷3.14=4(厘米)
学以致用
有一根长12.56厘米的铁丝,如果把它围成一个正方形,这个正方形的边长是多少厘米?如果把它围成一个圆,这个圆的直径是多少厘米?
解答:
12.56÷4 =3.14(厘米)
12.56÷3.14=4(厘米)
答:正方形的变长是3.14厘米,圆的直径是4厘米。
1.已知圆的周长,怎样求直径?
2.已知圆的周长,怎样求半径?
d=C÷π
r=C÷2π
学以致用
我国最高的摩天轮—“南昌之星”,转盘直径为153 m,坐着它转动一周,在空中转过的米数是多少?
C=πd
=3.14×153=480.42(m)
答:在空中转过的米数是480.42 m。
学以致用
一个铁环直径是60厘米,从操场东端滚到西端转了90圈,另一个铁环的直径是40厘米,它从东端滚到西端要转多少圈?
【答案】
(3.14×60×90)÷(3.14×40)
=16956÷125.6
=135(圈)
答:直径为40厘米的铁环从东端滚到西端要转135圈。
【解析】根据题意,可利用圆的周长公式分别计算出两个铁环的周长,然后再用第一个铁环的周长乘90就是操场从东到西的长度,再用操场从东到西的长度除以第二个铁环的周长就是第二个铁环转动的圈数,列式解答即可得到答案。
学以致用
第五部分
课堂小结
知识小结
当已知圆的半径,求圆的周长时,可以用
公式:C=2πr计算 。
根据圆的周长求出圆的直径或半径。
利用圆的周长的计算方法可以解决很多问题。通过联系,可以体会到数学知识与日常生活的密切关系,可以感受到数学知识的价值。
第六部分
课后作业
完成》同步练习。
课后作业
谢谢观看
下课!
