人教版数学六年级上册第五单元第5课时 扇形 课件(27张ppt)
文档属性
| 名称 | 人教版数学六年级上册第五单元第5课时 扇形 课件(27张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 00:00:00 | ||
图片预览








文档简介
六年级数学上册(RJ)教学课件
第五单元 圆
第5课时 扇形
目录
CONTENTS
情景导入
01
学习目标
02
探究与发现
03
学以致用
04
课后作业
06
课堂小结
05
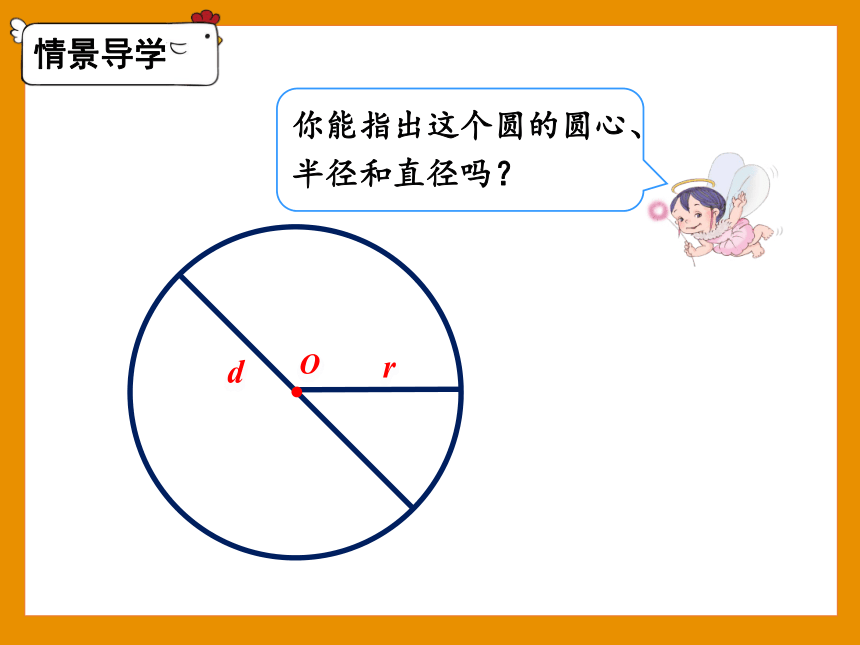
情景导学
第一部分
情景导学
O
r
d
你能指出这个圆的圆心、半径和直径吗?
情景导学
一个底面是圆形的蒙古包,沿地面量得周长25.12m,它的占地面积是多少平方米?
25.12÷3.14=8(m)
答:它的占地面积是50.24m?。
8÷2=4(m)
3.14×4?=50.24(m?)
第二部分
学习目标
学习目标
1.认识弧、圆心角以及他们之间的对应关系,认识扇形。
2.能准确判断圆心角和扇形。
3.理解扇形的大小在同一圆中与圆心角有关,了解扇形与所在圆的关系。
第三部分
探究与发现
探索与发现
什么是扇形?
这些物体的外形有什么相同的地方?
它们的外形都是扇形的。
探索与发现
A
B
O
圆心角
半径
半径
弧
图上A、B两点之间的部分叫做弧,读作“弧AB”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
顶点在圆心的角叫做圆心角。
探索与发现
A
B
C
D
O
O
O
O
下面各图中,哪些角是圆心角?
√
√
探索与发现
在同一个圆中,扇形的大小与什么有关系呢?
我发现在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。
探索与发现
180°
90°
以半圆为弧的扇形的圆心角是多少度?以 圆为弧的扇形呢?
4
1
以半圆为弧的扇形的圆心角是180°。
360× =90(度)
4
1
探索与发现
半径相同的两个扇形比较
圆心角大的那个扇形大。
O
O
探索与发现
圆心角相同的两个扇形比较
半径大的那个扇形大。
O
O
探索与发现
什么是圆环?
两个半径不相等的同心圆,大圆面积比小圆面积多的部分就是圆环 。
什么是扇环?
一个圆环被截得的部分叫做扇环 。
你知道如何求扇环的面积吗?
第四部分
学以致用
学以致用
指出下列物体中的扇形。
学以致用
A
B
C
D
O
O
O
O
下面各图中的实线围成的图形是扇形吗?
√
√
学以致用
在下列圆中画四个圆心角分别为45°、60°、90°、120°的扇形。
45°
60°
90°
120°
学以致用
你能求出下图中扇环的面积吗?
【解析】由图可判断出此扇环的面积为一个以5dm为外圆半径,2dm为内圆半径的圆环面积的1/4,根据圆环面积=外圆面积-内圆的面积求出圆环面积,就可求出扇环的面积。
外圆面积:3.14×5?=78.5 (dm?)
内圆面积:3.14×2?=12.56 (dm?)
圆环面积:78.5 – 12.56 = 65.94(dm?)
扇环面积:65.94÷4=16.458 ≈16.46(dm?)
(1)
学以致用
【解析】由图可判断出此扇环的面积由两个部分组成。均是一个以4dm为外圆半径,1dm为内圆半径的圆环面积的1/4,合在一起就是1/2个圆环。求出圆环面积,就可求出扇环的面积。
外圆面积:3.14×4?=50.24 (dm?)
内圆面积:3.14×1?=3.14 (dm?)
圆环面积:50.24 – 3.14 = 47.1(dm?)
扇环面积:47.1÷2=23.55(dm?)
(2)
第五部分
课堂小结
知识小结
1 . 圆上A、B两点之间的部分叫做弧,读作弧AB。一条弧和经过这个弧两端的两条半径所围成的图形叫做扇形。像∠AOB这样,顶点在圆心的角叫做圆心角。
0
A
B
半径
半径
2 . 一个圆环被截得的部分叫做扇环 。
第六部分
课后作业
完成同步练习。
课后作业
谢谢观看
下课!
第五单元 圆
第5课时 扇形
目录
CONTENTS
情景导入
01
学习目标
02
探究与发现
03
学以致用
04
课后作业
06
课堂小结
05
情景导学
第一部分
情景导学
O
r
d
你能指出这个圆的圆心、半径和直径吗?
情景导学
一个底面是圆形的蒙古包,沿地面量得周长25.12m,它的占地面积是多少平方米?
25.12÷3.14=8(m)
答:它的占地面积是50.24m?。
8÷2=4(m)
3.14×4?=50.24(m?)
第二部分
学习目标
学习目标
1.认识弧、圆心角以及他们之间的对应关系,认识扇形。
2.能准确判断圆心角和扇形。
3.理解扇形的大小在同一圆中与圆心角有关,了解扇形与所在圆的关系。
第三部分
探究与发现
探索与发现
什么是扇形?
这些物体的外形有什么相同的地方?
它们的外形都是扇形的。
探索与发现
A
B
O
圆心角
半径
半径
弧
图上A、B两点之间的部分叫做弧,读作“弧AB”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
顶点在圆心的角叫做圆心角。
探索与发现
A
B
C
D
O
O
O
O
下面各图中,哪些角是圆心角?
√
√
探索与发现
在同一个圆中,扇形的大小与什么有关系呢?
我发现在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。
探索与发现
180°
90°
以半圆为弧的扇形的圆心角是多少度?以 圆为弧的扇形呢?
4
1
以半圆为弧的扇形的圆心角是180°。
360× =90(度)
4
1
探索与发现
半径相同的两个扇形比较
圆心角大的那个扇形大。
O
O
探索与发现
圆心角相同的两个扇形比较
半径大的那个扇形大。
O
O
探索与发现
什么是圆环?
两个半径不相等的同心圆,大圆面积比小圆面积多的部分就是圆环 。
什么是扇环?
一个圆环被截得的部分叫做扇环 。
你知道如何求扇环的面积吗?
第四部分
学以致用
学以致用
指出下列物体中的扇形。
学以致用
A
B
C
D
O
O
O
O
下面各图中的实线围成的图形是扇形吗?
√
√
学以致用
在下列圆中画四个圆心角分别为45°、60°、90°、120°的扇形。
45°
60°
90°
120°
学以致用
你能求出下图中扇环的面积吗?
【解析】由图可判断出此扇环的面积为一个以5dm为外圆半径,2dm为内圆半径的圆环面积的1/4,根据圆环面积=外圆面积-内圆的面积求出圆环面积,就可求出扇环的面积。
外圆面积:3.14×5?=78.5 (dm?)
内圆面积:3.14×2?=12.56 (dm?)
圆环面积:78.5 – 12.56 = 65.94(dm?)
扇环面积:65.94÷4=16.458 ≈16.46(dm?)
(1)
学以致用
【解析】由图可判断出此扇环的面积由两个部分组成。均是一个以4dm为外圆半径,1dm为内圆半径的圆环面积的1/4,合在一起就是1/2个圆环。求出圆环面积,就可求出扇环的面积。
外圆面积:3.14×4?=50.24 (dm?)
内圆面积:3.14×1?=3.14 (dm?)
圆环面积:50.24 – 3.14 = 47.1(dm?)
扇环面积:47.1÷2=23.55(dm?)
(2)
第五部分
课堂小结
知识小结
1 . 圆上A、B两点之间的部分叫做弧,读作弧AB。一条弧和经过这个弧两端的两条半径所围成的图形叫做扇形。像∠AOB这样,顶点在圆心的角叫做圆心角。
0
A
B
半径
半径
2 . 一个圆环被截得的部分叫做扇环 。
第六部分
课后作业
完成同步练习。
课后作业
谢谢观看
下课!
