人教版八年级上册数学 13.4 课题学习 最短路径问题同步课件(17张)
文档属性
| 名称 | 人教版八年级上册数学 13.4 课题学习 最短路径问题同步课件(17张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 00:00:00 | ||
图片预览






文档简介
轴对称
?
第十三章
13.4 课题学习 最短路径问题
课堂导案
……………..…
1
课前学案
……………..…
2
3
课后练案
……………..…
4
能力培优
……………..…
5
核心目标
……………..…
核心目标
通过对最短路径问题的探索,进一步理解和掌握两点之间线段最短和垂线段最短.
课前学案
1.两点的所有连线中,_________最短.
2.连接直线外一点与直线上各点的所有连线中,__________最短.
线段
垂线段
课堂导案
【例题】如下图,小河CD边有两个村庄A村、B村,现要在河边建一自来水厂E为A村与B村供水,自来水厂建在什么地方到A村、B村的距离和最小?请在下图中找出点E的位置.(保留作图痕迹,不写作法)
课堂导案
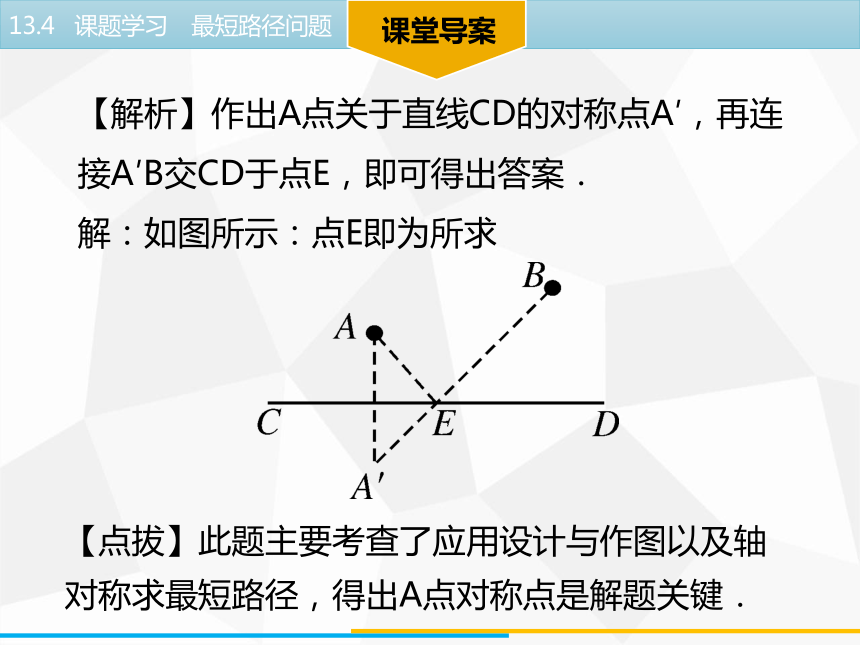
【解析】作出A点关于直线CD的对称点A′,再连接A′B交CD于点E,即可得出答案.
解:如图所示:点E即为所求
【点拔】此题主要考查了应用设计与作图以及轴对称求最短路径,得出A点对称点是解题关键.
课堂导案
1.已知:如下图所示,
(1)作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
(2)在x轴上画出点P,使PA+PC最小.
A'
B'
C'
C''
P
课堂导案
2.如下图,已知线段AB,在直线l上找到一点C,使得△ABC的周长最小,在图中作出C点.(尺规作图,不写作法,保留作图痕迹)
C
B'
课后练案
3.如下图,△ABC,AB=5,BC=4,AC=3.
(1)用直尺和圆规作边AB的垂直平分线MN;
(2)在直线MN上找一点D,使△ADC周长最小,并写出△ADC最小周长是__________.
7
N
D
C’
M
课后练案
4.如下图,两个村庄A和B被一条河隔开,现要在河上架设一座桥CD.请你为两村设计桥址,使由A村到B村的距离最小(假定两河岸m、n是平行的,且桥要与河垂直).要求写出作法,并说明理由.
过点B作BE⊥n且使BE等于河宽,连接AE交直线m于C,作CD∥BE交直线n于D,则CD为所求的桥址.理由:两点之间,线段最短.
D
E
C
能力培优
5.如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.
(1)若∠ABC=70°,则∠NMA的度数是________度.
50
能力培优
(2)若AB=8cm,△MBC的周长是14cm.
①求BC的长度;
∵MN是AB的垂直平分线,
∴AM=BM,
∴△MBC的周长=BM+CM+BC=AM+CM+BC=AC+BC,
∵AB=8,△MBC的周长是14,
∴BC=14-8=6;
能力培优
②若点P为直线MN上一点,请你直接写出△PBC周长的最小值.
当点P与M重合时,△PBC周长的值最小,
理由:∵PB+PC=PA+PC,PA+PC≥AC,∴P与M重合时,PA+PC=AC,此时PB+PC最小,
∴△PBC周长的最小值=AC+BC=8+6=14.
能力培优
6.如图,在△ABC的一边AB上有一点P.
能力培优
(1)能否在另外两边AC和BC上各找一点M、N,使得△PMN的周长最短?若能,请画出点M、N的位置,若不能,请说明理由;
①作出点P关于AC、BC的对称点D、G.
②连接DG交AC、BC于点M、N.点M、N即为所求.
能力培优
(2)若∠ACB=52°,在(1)的条件下,求出∠MPN的度数.
设PD交AC于E,PG交BC于F,
∵PD⊥AC,PG⊥BC,∴∠PEC=∠PFC=90°.
∴∠C+∠EPF=180°.
∵∠C=52°,∴∠EPF=128°.
∵∠D+∠G+∠EPF=180°,∴∠D+∠G=52°.由对称可知:∠G=∠GPN,∠D=∠DPM,∴∠GPN+∠DPM=52°.
∴∠MPN=128°-52°=76°.
感谢聆听
?
第十三章
13.4 课题学习 最短路径问题
课堂导案
……………..…
1
课前学案
……………..…
2
3
课后练案
……………..…
4
能力培优
……………..…
5
核心目标
……………..…
核心目标
通过对最短路径问题的探索,进一步理解和掌握两点之间线段最短和垂线段最短.
课前学案
1.两点的所有连线中,_________最短.
2.连接直线外一点与直线上各点的所有连线中,__________最短.
线段
垂线段
课堂导案
【例题】如下图,小河CD边有两个村庄A村、B村,现要在河边建一自来水厂E为A村与B村供水,自来水厂建在什么地方到A村、B村的距离和最小?请在下图中找出点E的位置.(保留作图痕迹,不写作法)
课堂导案
【解析】作出A点关于直线CD的对称点A′,再连接A′B交CD于点E,即可得出答案.
解:如图所示:点E即为所求
【点拔】此题主要考查了应用设计与作图以及轴对称求最短路径,得出A点对称点是解题关键.
课堂导案
1.已知:如下图所示,
(1)作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
(2)在x轴上画出点P,使PA+PC最小.
A'
B'
C'
C''
P
课堂导案
2.如下图,已知线段AB,在直线l上找到一点C,使得△ABC的周长最小,在图中作出C点.(尺规作图,不写作法,保留作图痕迹)
C
B'
课后练案
3.如下图,△ABC,AB=5,BC=4,AC=3.
(1)用直尺和圆规作边AB的垂直平分线MN;
(2)在直线MN上找一点D,使△ADC周长最小,并写出△ADC最小周长是__________.
7
N
D
C’
M
课后练案
4.如下图,两个村庄A和B被一条河隔开,现要在河上架设一座桥CD.请你为两村设计桥址,使由A村到B村的距离最小(假定两河岸m、n是平行的,且桥要与河垂直).要求写出作法,并说明理由.
过点B作BE⊥n且使BE等于河宽,连接AE交直线m于C,作CD∥BE交直线n于D,则CD为所求的桥址.理由:两点之间,线段最短.
D
E
C
能力培优
5.如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.
(1)若∠ABC=70°,则∠NMA的度数是________度.
50
能力培优
(2)若AB=8cm,△MBC的周长是14cm.
①求BC的长度;
∵MN是AB的垂直平分线,
∴AM=BM,
∴△MBC的周长=BM+CM+BC=AM+CM+BC=AC+BC,
∵AB=8,△MBC的周长是14,
∴BC=14-8=6;
能力培优
②若点P为直线MN上一点,请你直接写出△PBC周长的最小值.
当点P与M重合时,△PBC周长的值最小,
理由:∵PB+PC=PA+PC,PA+PC≥AC,∴P与M重合时,PA+PC=AC,此时PB+PC最小,
∴△PBC周长的最小值=AC+BC=8+6=14.
能力培优
6.如图,在△ABC的一边AB上有一点P.
能力培优
(1)能否在另外两边AC和BC上各找一点M、N,使得△PMN的周长最短?若能,请画出点M、N的位置,若不能,请说明理由;
①作出点P关于AC、BC的对称点D、G.
②连接DG交AC、BC于点M、N.点M、N即为所求.
能力培优
(2)若∠ACB=52°,在(1)的条件下,求出∠MPN的度数.
设PD交AC于E,PG交BC于F,
∵PD⊥AC,PG⊥BC,∴∠PEC=∠PFC=90°.
∴∠C+∠EPF=180°.
∵∠C=52°,∴∠EPF=128°.
∵∠D+∠G+∠EPF=180°,∴∠D+∠G=52°.由对称可知:∠G=∠GPN,∠D=∠DPM,∴∠GPN+∠DPM=52°.
∴∠MPN=128°-52°=76°.
感谢聆听
