人教版数学九年级上册:22.1.4《二次函数y=ɑx?+bx+c的图象和性质》 课件(第一课时 共66张)
文档属性
| 名称 | 人教版数学九年级上册:22.1.4《二次函数y=ɑx?+bx+c的图象和性质》 课件(第一课时 共66张) |  | |
| 格式 | pptx | ||
| 文件大小 | 936.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 11:05:08 | ||
图片预览







文档简介
(共66张PPT)
二次函数y=ɑx?+bx+c的图象和性质
第一课时
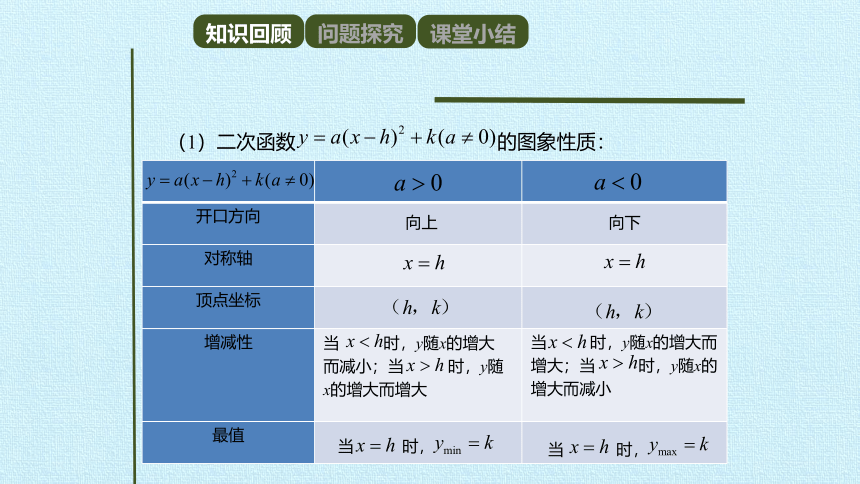
开口方向
对称轴
顶点坐标
增减性
最值
知识回顾
问题探究
课堂小结
(1)二次函数
的图象性质:
向上
当
时,y随x的增大而减小;当
时,y随x的增大而增大
当
时,y随x的增大而增大;当
时,y随x的增大而减小
向下
当
时,
当
时,
知识回顾
问题探究
课堂小结
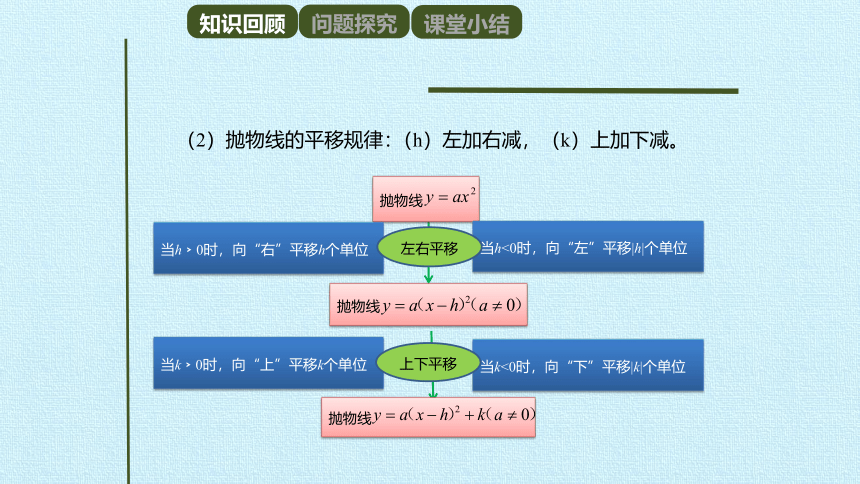
(2)抛物线的平移规律:
(h)左加右减,(k)上加下减。
抛物线
抛物线
当h﹥0时,向“右”平移h个单位
当h<0时,向“左”平移|h|个单位
当k﹥0时,向“上”平移k个单位
当k<0时,向“下”平移|k|个单位
抛物线
左右平移
上下平移
知识回顾
问题探究
课堂小结
活动1
探究一:从旧知识过渡到新知识。
复习配方
填空:(1)x2+4x+9=(x+
)2+
;
(2)x2-5x+8=(x-
)2+
。
2
5
总结规律:
当二次项的系数为1时,常数项须配一次项系数一半的平方。
知识回顾
问题探究
课堂小结
活动1
探究二:用配方法求抛物线y=ax2+bx+c的顶点坐标、对称轴。
合作探究
重点、难点知识★▲
例1画函数
的图象,并指出它的开口方向、对称轴和顶点坐标。
分析:首先要用配方法将函数写成y=a(x-h)2+k的形式;然后,确定函数图象的开口方向、对称轴与顶点坐标;接下来,利用函数的对称性列表、描点、连线。
知识回顾
问题探究
课堂小结
活动1
探究二:用配方法求抛物线y=ax2+bx+c的顶点坐标、对称轴。
重点、难点知识★▲
解:
所以它的开口向上,对称轴是x=6,
顶点坐标是(6,3)。
同学们自己画图!
归纳:
一般式化为顶点式的思路:
(1)二次项系数化为1;
(2)加、减一次项系数一半的平方;
(3)写成平方的形式。
例1画函数
的图象,并指出它的开口方向、对称轴和顶点坐标。
合作探究
知识回顾
问题探究
课堂小结
活动2
探究二:用配方法求抛物线y=ax2+bx+c的顶点坐标、对称轴。
小组讨论
重点、难点知识★▲
如果每次都采取“配方”,岂不是很麻烦?有更好的办法吗?
例2求二次函数y=ax?+bx+c的对称轴和顶点坐标。
解:把二次函数y=ax?+bx+c的右边配方,得
知识回顾
问题探究
课堂小结
活动2
探究二:用配方法求抛物线y=ax2+bx+c的顶点坐标、对称轴。
重点、难点知识★▲
点拨:
1.运用配方法,可以将二次函数表达式的两种形式y=ax2+bx+c与y=a(x-h)2+k相互转化。
将二次函数y=ax2+bx+c(一般式)转化为y=a(x-h)2+k(顶点式)的形式,
即:
则:
2.在二次函数y=ax2+bx+c与二次函数y=a(x-h)2+k中,
小组讨论
知识回顾
问题探究
课堂小结
活动
重点、难点知识★▲
探究三:二次函数的图象及性质。
师生共研,探究性质
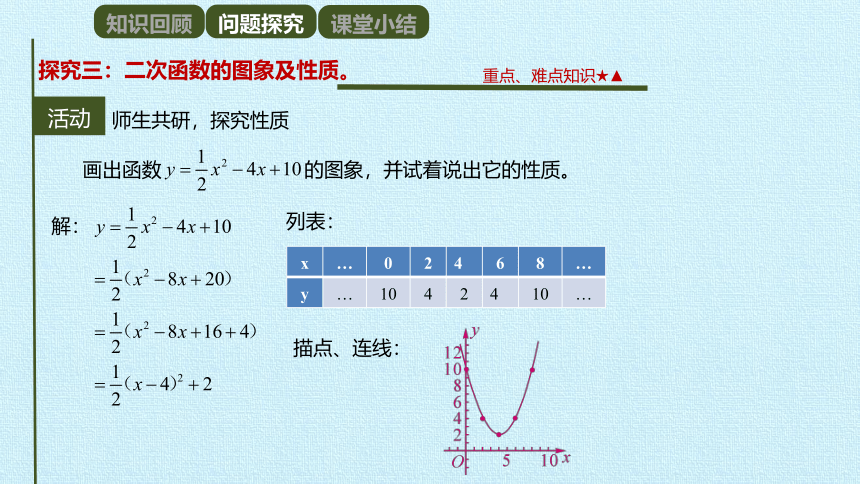
画出函数
的图象,并试着说出它的性质。
解:
列表:
x
…
0
2
4
6
8
…
y
…
10
4
2
4
10
…
描点、连线:
知识回顾
问题探究
课堂小结
活动
重点、难点知识★▲
探究三:二次函数的图象及性质。
观察图象知:
开口向上,对称轴是x=4,
顶点坐标是(4,2)。
当x>4时,y随x的增大而增大;
当x<4时,y随x的增大而减小。
当x=4时,函数y取最小值2。
师生共研,探究性质
画出函数
的图象,并试着说出它的性质。
知识回顾
问题探究
课堂小结
重点、难点知识★▲
探究三:二次函数的图象及性质。
思考、讨论下列问题:
1.对于任意一个二次函数y=ax2+bx+c(a≠0),如何确定它的图象的开口方向、对称轴和顶点坐标?你能把结果写出来吗?
2.观察二次函数y=ax2+bx+c(a≠0)的图象,在对称轴的左右两侧,y随x的增大有什么变化规律?
3.函数的最大值或最小值与函数图象的开口方向有什么关系?这个值与函数图象的顶点坐标有什么关系?
4.你能归纳总结二次函数y=ax2+bx+c(a≠0)的图象和性质吗?
活动
师生共研,探究性质。
知识回顾
问题探究
课堂小结
重点、难点知识★▲
探究三:二次函数的图象及性质
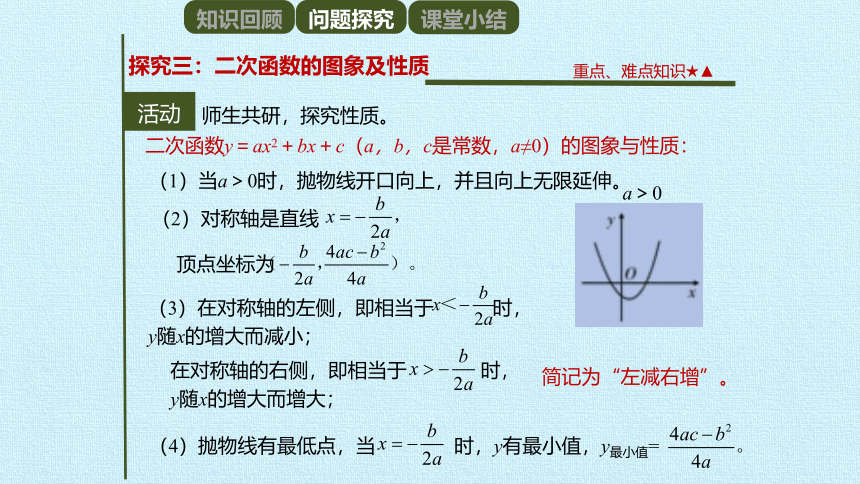
二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象与性质:
a>0
(1)当a>0时,抛物线开口向上,并且向上无限延伸。
(2)对称轴是直线
顶点坐标为
(3)在对称轴的左侧,即相当于
时,
y随x的增大而减小;
在对称轴的右侧,即相当于
时,
y随x的增大而增大;
简记为“左减右增”。
(4)抛物线有最低点,当
时,y有最小值,y最小值=
活动
师生共研,探究性质。
知识回顾
问题探究
课堂小结
重点、难点知识★▲
探究三:二次函数的图象及性质
二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象与性质:
a<0
(1)当a<0时,抛物线开口向下,并且向下无限延伸。
(2)对称轴是直线
顶点坐标为
(3)在对称轴的左侧,即相当于
时,
y随x的增大而增大;
在对称轴的右侧,即相当于
时,
y随x的增大而减小;
简记为“左增右减”。
(4)抛物线有最高点,当
时,y有最大值,y最大值=
活动
师生共研,探究性质
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动1
基础型例题
例1把下面的二次函数的一般式化成顶点式:
【解题过程】
解法一:用配方法:
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动1
【思路点拨】一般式化为顶点式有两种方法,一种是配方法,另一种是代入公式法。
例1把下面的二次函数的一般式化成顶点式:
基础型例题
【解题过程】
解法二:用公式法:
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动1
基础型例题
练习:若二次函数y=x2+bx+5配方后为y=(x-2)2+k,则b,k的值分别为(
)
A.0,5B.0,1C.-4,5D.-4,1
解:∵y=(x-2)2+k=x2-4x+4+k,∴b=-4,4+k=5,∴k=1,
故选D。
D
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动1
基础型例题
例2已知:抛物线
(1)直接写出抛物线的开口方向、对称轴、顶点坐标;
(2)求抛物线与x轴的交点坐标、与y轴的交点坐标;
(3)当x为何值时,y随x的增大而增大?
【解题过程】
解:(1)开口向上,对称轴为直线x=1,顶点坐标为(1,-8)。
(2)令y=0,得
解得
所以与x轴的交点坐标为(-1,0),(3,0)。
令x=0,得y=-6,所以与y轴的交点坐标为(0,-6)。
(3)当x≥1时,y随x的增大而增大。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动1
基础型例题
练习:若点A(2,y1)、B(3,y2)是二次函数y=x2-2x+1的图象上两点,则y1与y2的大小关系为y1 y2(填“>”、“<”、“=”)。
【解题过程】
解:∵二次函数y=x2﹣2x+1的图象的对称轴是x=1,在对称轴的右侧y随x的增大而增大,
∵点A(2,y1)、B(3,y2)是二次函数y=x2﹣2x+1的图象上两点,1<2<3,
∴y1<y2。
<
【思路点拨】根据已知条件求出二次函数的图象的对称轴,再根据点A、B的横坐标的大小即可判断出y1与y2的大小关系。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动2
提升型例题
例3已知
那么函数y=﹣2x2+8x﹣6的最大值是( )
﹣10.5B.2C.﹣2.5D.﹣6
【解题过程】
解:∵y=﹣2x2+8x﹣6=﹣2(x﹣2)2+2。
∴该抛物线的对称轴是x=2,且在x<2上y随x的增大而增大。
又∵
∴当
时,y取最大值,
C
【思路点拨】确定一个二次函数的最值,首先看自变量的取值范围,当自变量取全体实数时,其最值为抛物线顶点坐标的纵坐标;当自变量取某个范围时,要分别求出顶点和函数端点处的函数值,比较这些函数值,从而获得最值。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动2
提升型例题
…
-2
-1
0
1
2
…
…
0
4
6
6
4
…
从上表可知,下列说法中正确的是 。(填写序号)
①抛物线与x轴的一个交点为(3,0);
②函数
的最大值为6;
③抛物线的对称轴是
④在对称轴左侧,y随x增大而增大。
【思路点拨】题中给出表格,可根据所给数据,求出函数解析式,再据此即可作出判断;也可根据表格中的数据,抛物线的对称性,以及二次函数的图象性质,进行判断。
练习:抛
物线
上部分点的横坐标x,纵坐标y的对应值如下表:
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动2
提升型例题
【解题过程】
解法一:略。(请同学们自己完成)
解法二:
根据表格中的数据,抛物线的对称性,观察抛物线的对称轴是
③选项正确;
∵抛物线与x轴的一个交点为(-2,0),∴抛物线与x轴的另一个交点为(3,0),①选项正确;
∵抛物线过(0,6)、(1,6)两点,∴函数
的最大值不可能为6,②选项错误;
观察表格知,在对称轴左侧,y随x增大而增大,④选项正确。
故正确的是①③④。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动2
提升型例题
例4将抛物线y=ax?+bx+c向右平移3个单位长度,再向下平移2个单位长度,得到抛物线y=x?+2x+3,求a,b,c的值。
【解题过程】
解:∵y=x?+2x+3=(x+1)?+2,
∴把抛物线y=(x+1)?+2向左平移3个单位长度,再向上平移2个单位长度,
得到抛物线y=(x+4)?+4,
∴ax?+bx+c=(x+4)?+4=x?+8x+20,
∴a=1,b=8,c=20。
【思路点拨】此题应用了逆向思维。由抛物线y=ax?+bx+c变到抛物线y=x?+2x+3,不易求a,b,c的值;但反过来由抛物线y=x?+2x+3平移成抛物线y=ax?+bx+c就可轻松求解。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动2
提升型例题
练习:将抛物线
向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为
【思路点拨】先将一般式化为顶点式,根据左加右减,上加下减来平移。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用
活动3
探究型例题
例5如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C。
(1)求m的值;
【解题过程】
解:(1)将(3,0)代入二次函数解析式,得-32+2×3+m=0。
解得,m=3。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动3
(2)求点B的坐标;
解:(2)二次函数解析式为y=-x2+2x+3,令y=0,得-x2+2x+3=0。
解得x=3或x=-1。
∴点B的坐标为(-1,0)。
探究型例题
例5如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C。
【解题过程】
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动3
【思路点拨】解题的关键是掌握二次函数与一元二次方程的关系,底相同且面积相等的两个三角形高相等。
探究型例题
例5如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C。
【解题过程】
(3)该二次函数图象上有一点D(x,y)(其中x>0,y>0),使
求点D的坐标。
解:(3)∵
点D在第一象限,
∴点C、D关于二次函数对称轴对称。
∵由二次函数解析式可得其对称轴为x=1,点C的坐标为(0,3),
∴点D的坐标为(2,3)。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动3
探究型例题
练习:两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用
表示,而且左右两条抛物线关于y轴对称。
⑴钢缆的最低点到桥面的距离是多少?
【解题过程】
解:(1)
因此钢缆的最低点到桥面的距离是1m。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动3
【解题过程】
解:(2)
(2)两条钢缆最低点之间的距离是多少?
探究型例题
练习:两条钢缆具有相同的抛物线形状。按照图中的直角坐标系,左面的一条抛物线可以用
表示,而且左右两条抛物线关于y轴对称。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动3
(1)钢缆的最低点到桥面的距离是多少?
(2)两条钢缆最低点之间的距离是多少?
【思路点拨】
(1)将二次函数解析式配方,求得顶点坐标,从而获得钢缆的最低点到桥面的距离;
(2)由左右两条抛物线关于y轴对称,得出另一条抛物线解析式,可知它们的顶点坐标,从而求得两条钢缆最低点之间的距离。
探究型例题
练习:两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用
表示,而且左右两条抛物线关于y轴对称。
知识梳理
知识回顾
问题探究
课堂小结
归纳二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象与性质:
a>0
(1)当a>0时,抛物线开口向上,并且向上无限延伸.
(2)对称轴是直线
顶点坐标为
(3)在对称轴的左侧,即相当于
时,
y随x的增大而减小;
在对称轴的右侧,即相当于
时,
y随x的增大而增大;
简记为“左减右增”。
(4)抛物线有最低点,当
时,y有最小值,y最小值=
知识梳理
知识回顾
问题探究
课堂小结
归纳二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象与性质:
a<0
(1)当a<0时,抛物线开口向下,并且向下无限延伸。
(2)对称轴是直线
顶点坐标为
(3)在对称轴的左侧,即相当于
时,
y随x的增大而增大;
在对称轴的右侧,即相当于
时,
y随x的增大而减小;
简记为“左增右减”。
(4)抛物线有最高点,当
时,y有最大值,y最大值=
重难点归纳
知识回顾
问题探究
课堂小结
1.在画函数图象时,要在顶点的两边对称取点,画出的抛物线才能准确反映这个抛物线的特征。
2.抛物线y=ax2+bx+c是以直线为
对称轴的轴对称图形,有以下性质:
(1)抛物线上关于对称轴对称的两点纵坐标相等;抛物线上纵坐标相等的两点一定关于对称轴对称。
(2)如果抛物线交x轴于两点,那么这两点一定关于对称轴对称。
(3)若设抛物线上关于对称轴对称的两点横坐标为x1,x2,则抛物线的对称轴是直线
重难点归纳
知识回顾
问题探究
课堂小结
3.直接运用公式确定对称轴和顶点坐标时,不能忽视a,b,c的值的符号。
4.一般式的二次函数图象的平移法:对于一般式的图象平移,是先将一般式化成顶点式,再利用“左加右减,上加下减”规则来求解。
特别提醒:对于一般式的图象平移,一般式也可以不化成顶点式,只要熟记左加右减在所有的x上加减,上加下减在函数表达式的末尾加减即可。
重难点归纳
知识回顾
问题探究
课堂小结
5.二次函数
的最大值和最小值可以通过以下几种方法来解:
(1)配方法:
重难点归纳
知识回顾
问题探究
课堂小结
(2)公式法:
(3)图象法:
作出二次函数的图象,通过图象可以直观地观察到图象的最高点和最低点,此时的函数值为函数的最大值和最小值。
注意:通过二次函数的最值解答实际问题时,要注意自变量x的取值范围,要考虑实际问题的需要,有时
的函数值不在函数的取值范围内。
5.二次函数
的最大值和最小值可以通过以下几种方法来解:
二次函数y=ax?+bx+c的图象和性质
第二课时
知识回顾
问题探究
课堂小结
(1)二次函数表达式常见的三种形式是:
一般式:
y=ax?+bx+c
顶点式:
交点式:
(2)抛物线
的顶点坐标是:
(h,k)
知识回顾
问题探究
课堂小结
活动1
探究一:利用一般式求二次函数解析式。
回顾旧知,引出新知。
重点、难点知识★▲
问题1:一次函数y=kx+b(k≠0)有几个待定系数?通常需要已知几个点的坐标求出它的解析式?
2个
问题2:求一次函数解析式的方法是什么?它的一般步骤是什么?
待定系数法:(1)设:(表达式);(2)代:(坐标代入);(3)解:方程(组);(4)还原:(写解析式)
问题3:二次函数y=ax?+bx+c(a≠0)有几个待定系数?通常需要已知几个点的坐标求出它的解析式?
3个
知识回顾
问题探究
课堂小结
活动2
探究一:利用一般式求二次函数解析式。
重点、难点知识★▲
已知二次函数图象经过点(-3,0),(-1,0),(0,-3),试求出这个二次函数的解析式。
解析:设一般式y=ax2+bx+c,再把已知三点坐标代入得到关于a、b、c的方程组,然后解方程组求出a、b、c即可。
解:设这个二次函数的表达式是y=ax2+bx+c,
把(-3,0),(-1,0),(0,-3)代入y=ax2+bx+c得
解得
∴所求的二次函数的表达式是y=-x2-4x-3。
问题:已知抛物线上三个点如何确定二次函数解析式?
知识回顾
问题探究
课堂小结
活动2
探究一:利用一般式求二次函数解析式。
重点、难点知识★▲
一般式法求二次函数解析式的方法:
这种已知三点求二次函数解析式的方法叫做一般式法。
其步骤是:
①设函数解析式为y=ax2+bx+c;
②代入后得到一个三元一次方程组;
③解方程组得到a,b,c的值;
④把待定系数用数字换掉,写出函数解析式。
若题目给出了二次函数图象上三个点的坐标,则可采用一般式求解。
知识回顾
问题探究
课堂小结
活动
探究二:利用顶点式求二次函数解析式。
重点、难点知识★▲
问题:已知顶点坐标及图象上另一点坐标,能否求出二次函数解析式?如何进行?
已知抛物线的顶点坐标为M(1,-2),且经过点N(2,3),求此二次函数的解析式。
解析:因为抛物线的顶点坐标为M(1,-2),所以设此二次函数的解析式为y=a(x-1)2-2,把点N(2,3)代入解析式解答。
解:已知抛物线的顶点坐标为M(1,-2),
设此二次函数的解析式为y=a(x-1)2-2,
把点N(2,3)代入解析式,得a-2=3,即a=5,
∴此函数的解析式为y=5(x-1)2-2。
知识回顾
问题探究
课堂小结
活动
探究二:利用顶点式求二次函数解析式。
重点、难点知识★▲
顶点式法求二次函数解析式的方法:
这种知道抛物线的顶点坐标,求解析式的方法叫做顶点式法。
①设函数解析式是y=a(x-h)2+k;
②先代入顶点坐标,得到关于a的一元一次方程;
③将另一点的坐标代入原方程求出a值;
④a用数值换掉,写出函数解析式。
若题目给出了二次函数的顶点坐标,则采用顶点式求解简单。
知识回顾
问题探究
课堂小结
活动
探究三:利用交点式求二次函数解析式。
重点、难点知识★▲
问题:已知抛物线与x轴两交点坐标或一交点坐标和对称轴如何确定二次函数解析式?
已知抛物线经过两点A(1,0),B(0,-3),且对称轴是直线x=2,求此二次函数的解析式。
解析:可设交点式y=a(x-1)(x-3),然后把B点坐标代入求出a即可;
解:∵对称轴是直线x=2,
∴抛物线与x轴另一个交点坐标为(3,0)。
设抛物线解析式为y=a(x-1)(x-3),
把B(0,-3)代入得a(-1)×(-3)=-3,解得a=-1,
∴抛物线解析式为y=-(x-1)(x-3)=-x2+4x-3。
知识回顾
问题探究
课堂小结
活动
探究三:利用交点式求二次函数解析式。
重点、难点知识★▲
交点式法求二次函数解析式的步骤:
这种知道抛物线与x轴的交点坐标,求解析式的方法叫做交点式法。
①设函数解析式是
②先把两交点的横坐标x1,x2代入到解析式中,得到关于a的一元一次方程;
③将另一点的坐标代入原方程求出a值;
④a用数值换掉,写出函数解析式。
已知抛物线与x轴两交点或一交点和对称轴,则采用交点式求解简单。
知识回顾
问题探究
课堂小结
活动1
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
基础型例题
例1已知二次函数的图象与y轴交点的纵坐标为1,且经过点(2,5)和(-2,13),求这个二次函数的表达式。
【解题过程】
解:因为二次函数图象与y轴交点的纵坐标为1,所以c=1。
设二次函数的表达式为y=ax2+bx+1,
将点(2,5)和(-2,13)代入y=ax2+bx+1,得
解得
所以所求二次函数的表达式为y=2x2-2x+1。
【思路点拨】已知二次函数图象经过任意三点,可直接设表达式为一般式,代入可得三元一次方程组,解之即可求出待定系数。
知识回顾
问题探究
课堂小结
活动1
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
练习:已知二次函数的图象经过点A(3,0),B(2,-3),C(0,-3),求函数的表达式和对称轴。
【解题过程】
解:设函数表达式为y=ax2+bx+c,
因为二次函数的图象经过点A(3,0),B(2,-3),C(0,-3),则有
解得
∴函数的表达式为y=x2-2x-3,其对称轴为直线x=1。
基础型例题
知识回顾
问题探究
课堂小结
活动1
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
例2.已知抛物线的顶点是(1,2)且过点(2,3),求这个二次函数的表达式。
【解题过程】
解:已知顶点坐标设顶点式y=a(x-h)2+k,
∵顶点是(1,2),
∴设y=a(x-1)2+2,
又过点(2,3),
∴a(2-1)2+2=3,
∴a=1
∴y=(x-1)2+2,
即y=x2-2x+3。
【思路点拨】此题只告诉了两个点的坐标,但其中一点为顶点坐标,所以表达式可设顶点式:y=a(x-h)2+k,即可得到一个关于字母a的一元一次方程,再把另一点代入即可求出待定系数。在设表达式时注意h的符号。
基础型例题
知识回顾
问题探究
课堂小结
活动1
探究四:用待定系数法求二次函数解析式的训练
重点、难点知识★▲
【解题过程】
练习:已知一个二次函数的图象的顶点是(-1,2),且过点(0,
),求这个二次函数的表达式及与x轴交点的坐标。
解:已知顶点坐标设顶点式y=a(x-h)2+k,
∵顶点是(-1,2)
∴设y=a(x+1)2+2,
又过点(0,),
令y=0,
解得
∴与x轴交点坐标为(-3,0)、(1,0)。
基础型例题
知识回顾
问题探究
课堂小结
活动2
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
提升型例题
例3:已知抛物线经过三点(-3,0),(-1,0),(0,-3),试求出这个二次函数的表达式。
【解题过程】
解:∵(-3,0)(-1,0)是抛物线y=ax2+bx+c与x轴的交点。
所以可设这个二次函数的表达式是
(其中x1,x2为交点的横坐标)
因此得y=a(x+3)(x+1)。
再把点(0,-3)代入上式得
∴a(0+3)(0+1)=-3,解得a=-1,
∴所求的二次函数的表达式是y=-(x+3)(x+1),
即y=-x2-4x-3。
【思路点拨】因为已知点为抛物线与x轴的交点,表达式可设为交点式,再把第三点代入可得一元一次方程,较一般式所得的三元一次方程组简单,而顶点可根据顶点公式求出。
知识回顾
问题探究
课堂小结
活动2
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
练习:已知一抛物线经过三点A(-2,0)、B(1,0)、C(2,8)。试求该抛物线的表达式及顶点坐标。
【解题过程】
解:∵A(-2,0)、B(1,0)是抛物线与x轴两交点,
∴设表达式为y=a(x+2)(x-1),
把C(2,8)代入上式,
则有a(2+2)(2-1)=8,∴a=2。
∴此函数的表达式为y=2x2+2x-4。
提升型例题
其顶点坐标为
知识回顾
问题探究
课堂小结
活动2
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
例4:如图,已知二次函数的图象过A、C、B三点,点A的坐标为(﹣1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC。
(1)求点C的坐标;
(2)求二次函数的解析式,并化成一般形式。
【解题过程】
解:(1)∵点A的坐标为(﹣1,0),
点B的坐标为(4,0),∴OC=AB=5,
∴点C的坐标为(0,5);
(2)设二次函数解析式为:y=ax2+bx+5,
把A(﹣1,0)、B(4,0)代入原函数解析式得出:
所以这个二次函数的解析式为:
提升型例题
知识回顾
问题探究
课堂小结
活动2
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
【思路点拨】(1)根据题目所给的信息可以知道OC=AB=5,点C在y轴上可以写出点C的坐标;
(2)二次函数图象经过点A、B、C;这三个点的坐标已知,根据三点法确定这个二次函数解析式。
提升型例题
例4:如图,已知二次函数的图象过A、C、B三点,点A的坐标为(﹣1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC。
(1)求点C的坐标;
(2)求二次函数的解析式,并化成一般形式。
知识回顾
问题探究
课堂小结
活动2
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
练习:已知在直角坐标平面内,抛物线y=x2+bx+6经过x轴上两点A,B,点B的坐标为(3,0),与y轴相交于点C。
【解题过程】
解:(1)把点B的坐标(3,0)代入抛物线y=x2+bx+6,
得0=9+3b+6,解得b=﹣5,
所以抛物线的表达式y=x2﹣5x+6;
(2)∵抛物线的表达式y=x2﹣5x+6;
∴A(2,0),B(3,0),C(0,6),
提升型例题
(1)求抛物线的表达式;
(2)求
的面积。
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
探究型例题
例5:一个二次函数的图象经过点A(0,1),B(1,2),C(2,1),你能确定这个二次函数的表达式吗?你有几种方法?
【解题过程】
解法1:
∵二次函数图象与y轴的交点的纵坐标为1,∴c=1。
设二次函数的表达式为y=ax2+bx+1,
将点(1,2)和(2,1)分别代入y=ax2+bx+1,得
∴二次函数的表达式为y=-x2+2x+1。
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
由A(0,1),B(1,2),C(2,1)三个点的特征以及二次函数图象的对称性,可得点B(1,2)是函数图象的顶点坐标。
∴二次函数的表达式为y=a(x-1)2+2,
将点(0,1)代入y=a(x-1)2+2,
得a=-1。
∴二次函数的表达式为y=-(x-1)2+2,
即y=-x2+2x+1。
探究型例题
例5:一个二次函数的图象经过点A(0,1),B(1,2),C(2,1),你能确定这个二次函数的表达式吗?你有几种方法?
【解题过程】
解法2:
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
设二次函数的表达式为y=ax2+bx+c,
将点(0,1),(1,2)和(2,1)分别代入y=ax2+bx+c,得
∴二次函数的表达式为y=-x2+2x+1。
【思路点拨】分别找出用三种方法求解析式的条件,分别求解。
探究型例题
例5:一个二次函数的图象经过点A(0,1),B(1,2),C(2,1),你能确定这个二次函数的表达式吗?你有几种方法?
【解题过程】
解法3:
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练
重点、难点知识★▲
练习:如图所示,这是一名学生推铅球时,铅球行进高度y(m)与水平距离x(m)之间的图象,请求出其表达式。
【解题过程】
解:∵(4,3)是抛物线的顶点坐标,
∴设二次函数表达式为y=a(x-4)2+3,
把点(10,0)代入y=a(x-4)2+3,解得
因此铅球行进高度y(m)与水平距离x(m)之间的函数表达式为
【思路点拨】观察图象知,已知抛物线的顶点和另一点坐标,用顶点式求解。
探究型例题
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
例6:如图,已知二次函数
的图象经过点A和点B。
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
【解题过程】
解:(1)将x=-1,y=-1;x=3,y=-9分别代入
得
解得
∴二次函数的表达式为
(2)对称轴为x=2;顶点坐标为(2,-10)。
探究型例题
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
(3)点P(m,m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离。
(3)将(m,m)代入得
解得
∵m>0
∴
不合题意,舍去,
∴m=6。
∵点P与点Q关于对称轴x=2对称,
∴点Q到x轴的距离为6。
探究型例题
例6:如图,已知二次函数
的图象经过点A和点B。
【解题过程】
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m,m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离。
【思路点拨】
(1)用待定系数法求解析式;
(2)用对称轴方程和顶点坐标公式写出,也可用配方法写出;
(3)先将P(m,m)代入抛物线解析式求出m值,再求Q点坐标。
探究型例题
例6:如图,已知二次函数
的图象经过点A和点B。
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
练习:如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
【解题过程】
解:(1)∵抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),
∴将A与B坐标代入得:
解得:
则抛物线解析式为y=﹣x2+2x+3;
探究型例题
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练
重点、难点知识★▲
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长。
(2)点D为抛物线顶点,得D(1,4),
∵对称轴与x轴交于点E,
∴DE=4,OE=1,
∵B(﹣1,0),
∴BO=1,∴BE=2,
探究型例题
练习:如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
【解题过程】
在Rt
中,根据勾股定理得:
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
探究型例题
练习:如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长。
【思路点拨】
(1)将A与B代入抛物线解析式求出a与c的值,即可确定出抛物线解析式;
(2)利用顶点坐标公式表示出D点坐标,进而确定出E点坐标,得到DE与OE的长,根据B点
坐标求出BO的长,进而求出BE的长,在直角三角形BED中,利用勾股定理求出BD的长。
知识梳理
知识回顾
问题探究
课堂小结
(1)待定系数法求解析式的一般步骤:
①设:(表达式);②代:(坐标代入);③解:方程(组);④还原:(写解析式)
(2)待定系数法求二次函数解析式的一般方法:
已知条件
所选方法
已知三点坐标
用一般式法:
已知顶点坐标或对称轴或最值
用顶点法:
已知抛物线与x轴的两个交点
用交点法:
(其中x1,x2为交点的横坐标)
重难点归纳
知识回顾
问题探究
课堂小结
在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解。
一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;
当已知抛物线的顶点或对称轴或最大(小)值,常设其解析式为顶点式来求解;
当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解。
谢
谢
二次函数y=ɑx?+bx+c的图象和性质
第一课时
开口方向
对称轴
顶点坐标
增减性
最值
知识回顾
问题探究
课堂小结
(1)二次函数
的图象性质:
向上
当
时,y随x的增大而减小;当
时,y随x的增大而增大
当
时,y随x的增大而增大;当
时,y随x的增大而减小
向下
当
时,
当
时,
知识回顾
问题探究
课堂小结
(2)抛物线的平移规律:
(h)左加右减,(k)上加下减。
抛物线
抛物线
当h﹥0时,向“右”平移h个单位
当h<0时,向“左”平移|h|个单位
当k﹥0时,向“上”平移k个单位
当k<0时,向“下”平移|k|个单位
抛物线
左右平移
上下平移
知识回顾
问题探究
课堂小结
活动1
探究一:从旧知识过渡到新知识。
复习配方
填空:(1)x2+4x+9=(x+
)2+
;
(2)x2-5x+8=(x-
)2+
。
2
5
总结规律:
当二次项的系数为1时,常数项须配一次项系数一半的平方。
知识回顾
问题探究
课堂小结
活动1
探究二:用配方法求抛物线y=ax2+bx+c的顶点坐标、对称轴。
合作探究
重点、难点知识★▲
例1画函数
的图象,并指出它的开口方向、对称轴和顶点坐标。
分析:首先要用配方法将函数写成y=a(x-h)2+k的形式;然后,确定函数图象的开口方向、对称轴与顶点坐标;接下来,利用函数的对称性列表、描点、连线。
知识回顾
问题探究
课堂小结
活动1
探究二:用配方法求抛物线y=ax2+bx+c的顶点坐标、对称轴。
重点、难点知识★▲
解:
所以它的开口向上,对称轴是x=6,
顶点坐标是(6,3)。
同学们自己画图!
归纳:
一般式化为顶点式的思路:
(1)二次项系数化为1;
(2)加、减一次项系数一半的平方;
(3)写成平方的形式。
例1画函数
的图象,并指出它的开口方向、对称轴和顶点坐标。
合作探究
知识回顾
问题探究
课堂小结
活动2
探究二:用配方法求抛物线y=ax2+bx+c的顶点坐标、对称轴。
小组讨论
重点、难点知识★▲
如果每次都采取“配方”,岂不是很麻烦?有更好的办法吗?
例2求二次函数y=ax?+bx+c的对称轴和顶点坐标。
解:把二次函数y=ax?+bx+c的右边配方,得
知识回顾
问题探究
课堂小结
活动2
探究二:用配方法求抛物线y=ax2+bx+c的顶点坐标、对称轴。
重点、难点知识★▲
点拨:
1.运用配方法,可以将二次函数表达式的两种形式y=ax2+bx+c与y=a(x-h)2+k相互转化。
将二次函数y=ax2+bx+c(一般式)转化为y=a(x-h)2+k(顶点式)的形式,
即:
则:
2.在二次函数y=ax2+bx+c与二次函数y=a(x-h)2+k中,
小组讨论
知识回顾
问题探究
课堂小结
活动
重点、难点知识★▲
探究三:二次函数的图象及性质。
师生共研,探究性质
画出函数
的图象,并试着说出它的性质。
解:
列表:
x
…
0
2
4
6
8
…
y
…
10
4
2
4
10
…
描点、连线:
知识回顾
问题探究
课堂小结
活动
重点、难点知识★▲
探究三:二次函数的图象及性质。
观察图象知:
开口向上,对称轴是x=4,
顶点坐标是(4,2)。
当x>4时,y随x的增大而增大;
当x<4时,y随x的增大而减小。
当x=4时,函数y取最小值2。
师生共研,探究性质
画出函数
的图象,并试着说出它的性质。
知识回顾
问题探究
课堂小结
重点、难点知识★▲
探究三:二次函数的图象及性质。
思考、讨论下列问题:
1.对于任意一个二次函数y=ax2+bx+c(a≠0),如何确定它的图象的开口方向、对称轴和顶点坐标?你能把结果写出来吗?
2.观察二次函数y=ax2+bx+c(a≠0)的图象,在对称轴的左右两侧,y随x的增大有什么变化规律?
3.函数的最大值或最小值与函数图象的开口方向有什么关系?这个值与函数图象的顶点坐标有什么关系?
4.你能归纳总结二次函数y=ax2+bx+c(a≠0)的图象和性质吗?
活动
师生共研,探究性质。
知识回顾
问题探究
课堂小结
重点、难点知识★▲
探究三:二次函数的图象及性质
二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象与性质:
a>0
(1)当a>0时,抛物线开口向上,并且向上无限延伸。
(2)对称轴是直线
顶点坐标为
(3)在对称轴的左侧,即相当于
时,
y随x的增大而减小;
在对称轴的右侧,即相当于
时,
y随x的增大而增大;
简记为“左减右增”。
(4)抛物线有最低点,当
时,y有最小值,y最小值=
活动
师生共研,探究性质。
知识回顾
问题探究
课堂小结
重点、难点知识★▲
探究三:二次函数的图象及性质
二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象与性质:
a<0
(1)当a<0时,抛物线开口向下,并且向下无限延伸。
(2)对称轴是直线
顶点坐标为
(3)在对称轴的左侧,即相当于
时,
y随x的增大而增大;
在对称轴的右侧,即相当于
时,
y随x的增大而减小;
简记为“左增右减”。
(4)抛物线有最高点,当
时,y有最大值,y最大值=
活动
师生共研,探究性质
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动1
基础型例题
例1把下面的二次函数的一般式化成顶点式:
【解题过程】
解法一:用配方法:
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动1
【思路点拨】一般式化为顶点式有两种方法,一种是配方法,另一种是代入公式法。
例1把下面的二次函数的一般式化成顶点式:
基础型例题
【解题过程】
解法二:用公式法:
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动1
基础型例题
练习:若二次函数y=x2+bx+5配方后为y=(x-2)2+k,则b,k的值分别为(
)
A.0,5B.0,1C.-4,5D.-4,1
解:∵y=(x-2)2+k=x2-4x+4+k,∴b=-4,4+k=5,∴k=1,
故选D。
D
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动1
基础型例题
例2已知:抛物线
(1)直接写出抛物线的开口方向、对称轴、顶点坐标;
(2)求抛物线与x轴的交点坐标、与y轴的交点坐标;
(3)当x为何值时,y随x的增大而增大?
【解题过程】
解:(1)开口向上,对称轴为直线x=1,顶点坐标为(1,-8)。
(2)令y=0,得
解得
所以与x轴的交点坐标为(-1,0),(3,0)。
令x=0,得y=-6,所以与y轴的交点坐标为(0,-6)。
(3)当x≥1时,y随x的增大而增大。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动1
基础型例题
练习:若点A(2,y1)、B(3,y2)是二次函数y=x2-2x+1的图象上两点,则y1与y2的大小关系为y1 y2(填“>”、“<”、“=”)。
【解题过程】
解:∵二次函数y=x2﹣2x+1的图象的对称轴是x=1,在对称轴的右侧y随x的增大而增大,
∵点A(2,y1)、B(3,y2)是二次函数y=x2﹣2x+1的图象上两点,1<2<3,
∴y1<y2。
<
【思路点拨】根据已知条件求出二次函数的图象的对称轴,再根据点A、B的横坐标的大小即可判断出y1与y2的大小关系。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动2
提升型例题
例3已知
那么函数y=﹣2x2+8x﹣6的最大值是( )
﹣10.5B.2C.﹣2.5D.﹣6
【解题过程】
解:∵y=﹣2x2+8x﹣6=﹣2(x﹣2)2+2。
∴该抛物线的对称轴是x=2,且在x<2上y随x的增大而增大。
又∵
∴当
时,y取最大值,
C
【思路点拨】确定一个二次函数的最值,首先看自变量的取值范围,当自变量取全体实数时,其最值为抛物线顶点坐标的纵坐标;当自变量取某个范围时,要分别求出顶点和函数端点处的函数值,比较这些函数值,从而获得最值。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动2
提升型例题
…
-2
-1
0
1
2
…
…
0
4
6
6
4
…
从上表可知,下列说法中正确的是 。(填写序号)
①抛物线与x轴的一个交点为(3,0);
②函数
的最大值为6;
③抛物线的对称轴是
④在对称轴左侧,y随x增大而增大。
【思路点拨】题中给出表格,可根据所给数据,求出函数解析式,再据此即可作出判断;也可根据表格中的数据,抛物线的对称性,以及二次函数的图象性质,进行判断。
练习:抛
物线
上部分点的横坐标x,纵坐标y的对应值如下表:
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动2
提升型例题
【解题过程】
解法一:略。(请同学们自己完成)
解法二:
根据表格中的数据,抛物线的对称性,观察抛物线的对称轴是
③选项正确;
∵抛物线与x轴的一个交点为(-2,0),∴抛物线与x轴的另一个交点为(3,0),①选项正确;
∵抛物线过(0,6)、(1,6)两点,∴函数
的最大值不可能为6,②选项错误;
观察表格知,在对称轴左侧,y随x增大而增大,④选项正确。
故正确的是①③④。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动2
提升型例题
例4将抛物线y=ax?+bx+c向右平移3个单位长度,再向下平移2个单位长度,得到抛物线y=x?+2x+3,求a,b,c的值。
【解题过程】
解:∵y=x?+2x+3=(x+1)?+2,
∴把抛物线y=(x+1)?+2向左平移3个单位长度,再向上平移2个单位长度,
得到抛物线y=(x+4)?+4,
∴ax?+bx+c=(x+4)?+4=x?+8x+20,
∴a=1,b=8,c=20。
【思路点拨】此题应用了逆向思维。由抛物线y=ax?+bx+c变到抛物线y=x?+2x+3,不易求a,b,c的值;但反过来由抛物线y=x?+2x+3平移成抛物线y=ax?+bx+c就可轻松求解。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动2
提升型例题
练习:将抛物线
向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为
【思路点拨】先将一般式化为顶点式,根据左加右减,上加下减来平移。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用
活动3
探究型例题
例5如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C。
(1)求m的值;
【解题过程】
解:(1)将(3,0)代入二次函数解析式,得-32+2×3+m=0。
解得,m=3。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动3
(2)求点B的坐标;
解:(2)二次函数解析式为y=-x2+2x+3,令y=0,得-x2+2x+3=0。
解得x=3或x=-1。
∴点B的坐标为(-1,0)。
探究型例题
例5如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C。
【解题过程】
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动3
【思路点拨】解题的关键是掌握二次函数与一元二次方程的关系,底相同且面积相等的两个三角形高相等。
探究型例题
例5如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C。
【解题过程】
(3)该二次函数图象上有一点D(x,y)(其中x>0,y>0),使
求点D的坐标。
解:(3)∵
点D在第一象限,
∴点C、D关于二次函数对称轴对称。
∵由二次函数解析式可得其对称轴为x=1,点C的坐标为(0,3),
∴点D的坐标为(2,3)。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动3
探究型例题
练习:两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用
表示,而且左右两条抛物线关于y轴对称。
⑴钢缆的最低点到桥面的距离是多少?
【解题过程】
解:(1)
因此钢缆的最低点到桥面的距离是1m。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动3
【解题过程】
解:(2)
(2)两条钢缆最低点之间的距离是多少?
探究型例题
练习:两条钢缆具有相同的抛物线形状。按照图中的直角坐标系,左面的一条抛物线可以用
表示,而且左右两条抛物线关于y轴对称。
知识回顾
问题探究
课堂小结
探究四:二次函数的图象及性质的应用。
活动3
(1)钢缆的最低点到桥面的距离是多少?
(2)两条钢缆最低点之间的距离是多少?
【思路点拨】
(1)将二次函数解析式配方,求得顶点坐标,从而获得钢缆的最低点到桥面的距离;
(2)由左右两条抛物线关于y轴对称,得出另一条抛物线解析式,可知它们的顶点坐标,从而求得两条钢缆最低点之间的距离。
探究型例题
练习:两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用
表示,而且左右两条抛物线关于y轴对称。
知识梳理
知识回顾
问题探究
课堂小结
归纳二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象与性质:
a>0
(1)当a>0时,抛物线开口向上,并且向上无限延伸.
(2)对称轴是直线
顶点坐标为
(3)在对称轴的左侧,即相当于
时,
y随x的增大而减小;
在对称轴的右侧,即相当于
时,
y随x的增大而增大;
简记为“左减右增”。
(4)抛物线有最低点,当
时,y有最小值,y最小值=
知识梳理
知识回顾
问题探究
课堂小结
归纳二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象与性质:
a<0
(1)当a<0时,抛物线开口向下,并且向下无限延伸。
(2)对称轴是直线
顶点坐标为
(3)在对称轴的左侧,即相当于
时,
y随x的增大而增大;
在对称轴的右侧,即相当于
时,
y随x的增大而减小;
简记为“左增右减”。
(4)抛物线有最高点,当
时,y有最大值,y最大值=
重难点归纳
知识回顾
问题探究
课堂小结
1.在画函数图象时,要在顶点的两边对称取点,画出的抛物线才能准确反映这个抛物线的特征。
2.抛物线y=ax2+bx+c是以直线为
对称轴的轴对称图形,有以下性质:
(1)抛物线上关于对称轴对称的两点纵坐标相等;抛物线上纵坐标相等的两点一定关于对称轴对称。
(2)如果抛物线交x轴于两点,那么这两点一定关于对称轴对称。
(3)若设抛物线上关于对称轴对称的两点横坐标为x1,x2,则抛物线的对称轴是直线
重难点归纳
知识回顾
问题探究
课堂小结
3.直接运用公式确定对称轴和顶点坐标时,不能忽视a,b,c的值的符号。
4.一般式的二次函数图象的平移法:对于一般式的图象平移,是先将一般式化成顶点式,再利用“左加右减,上加下减”规则来求解。
特别提醒:对于一般式的图象平移,一般式也可以不化成顶点式,只要熟记左加右减在所有的x上加减,上加下减在函数表达式的末尾加减即可。
重难点归纳
知识回顾
问题探究
课堂小结
5.二次函数
的最大值和最小值可以通过以下几种方法来解:
(1)配方法:
重难点归纳
知识回顾
问题探究
课堂小结
(2)公式法:
(3)图象法:
作出二次函数的图象,通过图象可以直观地观察到图象的最高点和最低点,此时的函数值为函数的最大值和最小值。
注意:通过二次函数的最值解答实际问题时,要注意自变量x的取值范围,要考虑实际问题的需要,有时
的函数值不在函数的取值范围内。
5.二次函数
的最大值和最小值可以通过以下几种方法来解:
二次函数y=ax?+bx+c的图象和性质
第二课时
知识回顾
问题探究
课堂小结
(1)二次函数表达式常见的三种形式是:
一般式:
y=ax?+bx+c
顶点式:
交点式:
(2)抛物线
的顶点坐标是:
(h,k)
知识回顾
问题探究
课堂小结
活动1
探究一:利用一般式求二次函数解析式。
回顾旧知,引出新知。
重点、难点知识★▲
问题1:一次函数y=kx+b(k≠0)有几个待定系数?通常需要已知几个点的坐标求出它的解析式?
2个
问题2:求一次函数解析式的方法是什么?它的一般步骤是什么?
待定系数法:(1)设:(表达式);(2)代:(坐标代入);(3)解:方程(组);(4)还原:(写解析式)
问题3:二次函数y=ax?+bx+c(a≠0)有几个待定系数?通常需要已知几个点的坐标求出它的解析式?
3个
知识回顾
问题探究
课堂小结
活动2
探究一:利用一般式求二次函数解析式。
重点、难点知识★▲
已知二次函数图象经过点(-3,0),(-1,0),(0,-3),试求出这个二次函数的解析式。
解析:设一般式y=ax2+bx+c,再把已知三点坐标代入得到关于a、b、c的方程组,然后解方程组求出a、b、c即可。
解:设这个二次函数的表达式是y=ax2+bx+c,
把(-3,0),(-1,0),(0,-3)代入y=ax2+bx+c得
解得
∴所求的二次函数的表达式是y=-x2-4x-3。
问题:已知抛物线上三个点如何确定二次函数解析式?
知识回顾
问题探究
课堂小结
活动2
探究一:利用一般式求二次函数解析式。
重点、难点知识★▲
一般式法求二次函数解析式的方法:
这种已知三点求二次函数解析式的方法叫做一般式法。
其步骤是:
①设函数解析式为y=ax2+bx+c;
②代入后得到一个三元一次方程组;
③解方程组得到a,b,c的值;
④把待定系数用数字换掉,写出函数解析式。
若题目给出了二次函数图象上三个点的坐标,则可采用一般式求解。
知识回顾
问题探究
课堂小结
活动
探究二:利用顶点式求二次函数解析式。
重点、难点知识★▲
问题:已知顶点坐标及图象上另一点坐标,能否求出二次函数解析式?如何进行?
已知抛物线的顶点坐标为M(1,-2),且经过点N(2,3),求此二次函数的解析式。
解析:因为抛物线的顶点坐标为M(1,-2),所以设此二次函数的解析式为y=a(x-1)2-2,把点N(2,3)代入解析式解答。
解:已知抛物线的顶点坐标为M(1,-2),
设此二次函数的解析式为y=a(x-1)2-2,
把点N(2,3)代入解析式,得a-2=3,即a=5,
∴此函数的解析式为y=5(x-1)2-2。
知识回顾
问题探究
课堂小结
活动
探究二:利用顶点式求二次函数解析式。
重点、难点知识★▲
顶点式法求二次函数解析式的方法:
这种知道抛物线的顶点坐标,求解析式的方法叫做顶点式法。
①设函数解析式是y=a(x-h)2+k;
②先代入顶点坐标,得到关于a的一元一次方程;
③将另一点的坐标代入原方程求出a值;
④a用数值换掉,写出函数解析式。
若题目给出了二次函数的顶点坐标,则采用顶点式求解简单。
知识回顾
问题探究
课堂小结
活动
探究三:利用交点式求二次函数解析式。
重点、难点知识★▲
问题:已知抛物线与x轴两交点坐标或一交点坐标和对称轴如何确定二次函数解析式?
已知抛物线经过两点A(1,0),B(0,-3),且对称轴是直线x=2,求此二次函数的解析式。
解析:可设交点式y=a(x-1)(x-3),然后把B点坐标代入求出a即可;
解:∵对称轴是直线x=2,
∴抛物线与x轴另一个交点坐标为(3,0)。
设抛物线解析式为y=a(x-1)(x-3),
把B(0,-3)代入得a(-1)×(-3)=-3,解得a=-1,
∴抛物线解析式为y=-(x-1)(x-3)=-x2+4x-3。
知识回顾
问题探究
课堂小结
活动
探究三:利用交点式求二次函数解析式。
重点、难点知识★▲
交点式法求二次函数解析式的步骤:
这种知道抛物线与x轴的交点坐标,求解析式的方法叫做交点式法。
①设函数解析式是
②先把两交点的横坐标x1,x2代入到解析式中,得到关于a的一元一次方程;
③将另一点的坐标代入原方程求出a值;
④a用数值换掉,写出函数解析式。
已知抛物线与x轴两交点或一交点和对称轴,则采用交点式求解简单。
知识回顾
问题探究
课堂小结
活动1
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
基础型例题
例1已知二次函数的图象与y轴交点的纵坐标为1,且经过点(2,5)和(-2,13),求这个二次函数的表达式。
【解题过程】
解:因为二次函数图象与y轴交点的纵坐标为1,所以c=1。
设二次函数的表达式为y=ax2+bx+1,
将点(2,5)和(-2,13)代入y=ax2+bx+1,得
解得
所以所求二次函数的表达式为y=2x2-2x+1。
【思路点拨】已知二次函数图象经过任意三点,可直接设表达式为一般式,代入可得三元一次方程组,解之即可求出待定系数。
知识回顾
问题探究
课堂小结
活动1
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
练习:已知二次函数的图象经过点A(3,0),B(2,-3),C(0,-3),求函数的表达式和对称轴。
【解题过程】
解:设函数表达式为y=ax2+bx+c,
因为二次函数的图象经过点A(3,0),B(2,-3),C(0,-3),则有
解得
∴函数的表达式为y=x2-2x-3,其对称轴为直线x=1。
基础型例题
知识回顾
问题探究
课堂小结
活动1
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
例2.已知抛物线的顶点是(1,2)且过点(2,3),求这个二次函数的表达式。
【解题过程】
解:已知顶点坐标设顶点式y=a(x-h)2+k,
∵顶点是(1,2),
∴设y=a(x-1)2+2,
又过点(2,3),
∴a(2-1)2+2=3,
∴a=1
∴y=(x-1)2+2,
即y=x2-2x+3。
【思路点拨】此题只告诉了两个点的坐标,但其中一点为顶点坐标,所以表达式可设顶点式:y=a(x-h)2+k,即可得到一个关于字母a的一元一次方程,再把另一点代入即可求出待定系数。在设表达式时注意h的符号。
基础型例题
知识回顾
问题探究
课堂小结
活动1
探究四:用待定系数法求二次函数解析式的训练
重点、难点知识★▲
【解题过程】
练习:已知一个二次函数的图象的顶点是(-1,2),且过点(0,
),求这个二次函数的表达式及与x轴交点的坐标。
解:已知顶点坐标设顶点式y=a(x-h)2+k,
∵顶点是(-1,2)
∴设y=a(x+1)2+2,
又过点(0,),
令y=0,
解得
∴与x轴交点坐标为(-3,0)、(1,0)。
基础型例题
知识回顾
问题探究
课堂小结
活动2
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
提升型例题
例3:已知抛物线经过三点(-3,0),(-1,0),(0,-3),试求出这个二次函数的表达式。
【解题过程】
解:∵(-3,0)(-1,0)是抛物线y=ax2+bx+c与x轴的交点。
所以可设这个二次函数的表达式是
(其中x1,x2为交点的横坐标)
因此得y=a(x+3)(x+1)。
再把点(0,-3)代入上式得
∴a(0+3)(0+1)=-3,解得a=-1,
∴所求的二次函数的表达式是y=-(x+3)(x+1),
即y=-x2-4x-3。
【思路点拨】因为已知点为抛物线与x轴的交点,表达式可设为交点式,再把第三点代入可得一元一次方程,较一般式所得的三元一次方程组简单,而顶点可根据顶点公式求出。
知识回顾
问题探究
课堂小结
活动2
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
练习:已知一抛物线经过三点A(-2,0)、B(1,0)、C(2,8)。试求该抛物线的表达式及顶点坐标。
【解题过程】
解:∵A(-2,0)、B(1,0)是抛物线与x轴两交点,
∴设表达式为y=a(x+2)(x-1),
把C(2,8)代入上式,
则有a(2+2)(2-1)=8,∴a=2。
∴此函数的表达式为y=2x2+2x-4。
提升型例题
其顶点坐标为
知识回顾
问题探究
课堂小结
活动2
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
例4:如图,已知二次函数的图象过A、C、B三点,点A的坐标为(﹣1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC。
(1)求点C的坐标;
(2)求二次函数的解析式,并化成一般形式。
【解题过程】
解:(1)∵点A的坐标为(﹣1,0),
点B的坐标为(4,0),∴OC=AB=5,
∴点C的坐标为(0,5);
(2)设二次函数解析式为:y=ax2+bx+5,
把A(﹣1,0)、B(4,0)代入原函数解析式得出:
所以这个二次函数的解析式为:
提升型例题
知识回顾
问题探究
课堂小结
活动2
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
【思路点拨】(1)根据题目所给的信息可以知道OC=AB=5,点C在y轴上可以写出点C的坐标;
(2)二次函数图象经过点A、B、C;这三个点的坐标已知,根据三点法确定这个二次函数解析式。
提升型例题
例4:如图,已知二次函数的图象过A、C、B三点,点A的坐标为(﹣1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC。
(1)求点C的坐标;
(2)求二次函数的解析式,并化成一般形式。
知识回顾
问题探究
课堂小结
活动2
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
练习:已知在直角坐标平面内,抛物线y=x2+bx+6经过x轴上两点A,B,点B的坐标为(3,0),与y轴相交于点C。
【解题过程】
解:(1)把点B的坐标(3,0)代入抛物线y=x2+bx+6,
得0=9+3b+6,解得b=﹣5,
所以抛物线的表达式y=x2﹣5x+6;
(2)∵抛物线的表达式y=x2﹣5x+6;
∴A(2,0),B(3,0),C(0,6),
提升型例题
(1)求抛物线的表达式;
(2)求
的面积。
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
探究型例题
例5:一个二次函数的图象经过点A(0,1),B(1,2),C(2,1),你能确定这个二次函数的表达式吗?你有几种方法?
【解题过程】
解法1:
∵二次函数图象与y轴的交点的纵坐标为1,∴c=1。
设二次函数的表达式为y=ax2+bx+1,
将点(1,2)和(2,1)分别代入y=ax2+bx+1,得
∴二次函数的表达式为y=-x2+2x+1。
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
由A(0,1),B(1,2),C(2,1)三个点的特征以及二次函数图象的对称性,可得点B(1,2)是函数图象的顶点坐标。
∴二次函数的表达式为y=a(x-1)2+2,
将点(0,1)代入y=a(x-1)2+2,
得a=-1。
∴二次函数的表达式为y=-(x-1)2+2,
即y=-x2+2x+1。
探究型例题
例5:一个二次函数的图象经过点A(0,1),B(1,2),C(2,1),你能确定这个二次函数的表达式吗?你有几种方法?
【解题过程】
解法2:
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
设二次函数的表达式为y=ax2+bx+c,
将点(0,1),(1,2)和(2,1)分别代入y=ax2+bx+c,得
∴二次函数的表达式为y=-x2+2x+1。
【思路点拨】分别找出用三种方法求解析式的条件,分别求解。
探究型例题
例5:一个二次函数的图象经过点A(0,1),B(1,2),C(2,1),你能确定这个二次函数的表达式吗?你有几种方法?
【解题过程】
解法3:
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练
重点、难点知识★▲
练习:如图所示,这是一名学生推铅球时,铅球行进高度y(m)与水平距离x(m)之间的图象,请求出其表达式。
【解题过程】
解:∵(4,3)是抛物线的顶点坐标,
∴设二次函数表达式为y=a(x-4)2+3,
把点(10,0)代入y=a(x-4)2+3,解得
因此铅球行进高度y(m)与水平距离x(m)之间的函数表达式为
【思路点拨】观察图象知,已知抛物线的顶点和另一点坐标,用顶点式求解。
探究型例题
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
例6:如图,已知二次函数
的图象经过点A和点B。
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
【解题过程】
解:(1)将x=-1,y=-1;x=3,y=-9分别代入
得
解得
∴二次函数的表达式为
(2)对称轴为x=2;顶点坐标为(2,-10)。
探究型例题
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
(3)点P(m,m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离。
(3)将(m,m)代入得
解得
∵m>0
∴
不合题意,舍去,
∴m=6。
∵点P与点Q关于对称轴x=2对称,
∴点Q到x轴的距离为6。
探究型例题
例6:如图,已知二次函数
的图象经过点A和点B。
【解题过程】
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m,m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离。
【思路点拨】
(1)用待定系数法求解析式;
(2)用对称轴方程和顶点坐标公式写出,也可用配方法写出;
(3)先将P(m,m)代入抛物线解析式求出m值,再求Q点坐标。
探究型例题
例6:如图,已知二次函数
的图象经过点A和点B。
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
练习:如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
【解题过程】
解:(1)∵抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),
∴将A与B坐标代入得:
解得:
则抛物线解析式为y=﹣x2+2x+3;
探究型例题
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练
重点、难点知识★▲
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长。
(2)点D为抛物线顶点,得D(1,4),
∵对称轴与x轴交于点E,
∴DE=4,OE=1,
∵B(﹣1,0),
∴BO=1,∴BE=2,
探究型例题
练习:如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
【解题过程】
在Rt
中,根据勾股定理得:
知识回顾
问题探究
课堂小结
活动3
探究四:用待定系数法求二次函数解析式的训练。
重点、难点知识★▲
探究型例题
练习:如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长。
【思路点拨】
(1)将A与B代入抛物线解析式求出a与c的值,即可确定出抛物线解析式;
(2)利用顶点坐标公式表示出D点坐标,进而确定出E点坐标,得到DE与OE的长,根据B点
坐标求出BO的长,进而求出BE的长,在直角三角形BED中,利用勾股定理求出BD的长。
知识梳理
知识回顾
问题探究
课堂小结
(1)待定系数法求解析式的一般步骤:
①设:(表达式);②代:(坐标代入);③解:方程(组);④还原:(写解析式)
(2)待定系数法求二次函数解析式的一般方法:
已知条件
所选方法
已知三点坐标
用一般式法:
已知顶点坐标或对称轴或最值
用顶点法:
已知抛物线与x轴的两个交点
用交点法:
(其中x1,x2为交点的横坐标)
重难点归纳
知识回顾
问题探究
课堂小结
在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解。
一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;
当已知抛物线的顶点或对称轴或最大(小)值,常设其解析式为顶点式来求解;
当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解。
谢
谢
同课章节目录
