人教版数学九年级上册:22.3《实际问题与二次函数》 课件(共33张)
文档属性
| 名称 | 人教版数学九年级上册:22.3《实际问题与二次函数》 课件(共33张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 382.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 00:00:00 | ||
图片预览











文档简介
实际问题与二次函数
知识回顾
问题探究
课堂小结
(1)营销问题的基本等量关系:
利润=每件利润×销售量
每件利润=每件售价﹣每件进价。
(2)抛物线 的最值问题:
①若a>0,则当x= 时,y最小值= 。
②若a<0,则当x= 时,y最大值= 。
活动1
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
回顾旧知,回忆销售问题中常见概念和公式。
成本价;定价;售价;利润;销量;利润率;定价;
销售问题中一般都会涉及哪些名词?它们之间的数量关系是什么?
利润=每件利润×销售量
每件利润=每件售价﹣每件进价。
知识回顾
问题探究
课堂小结
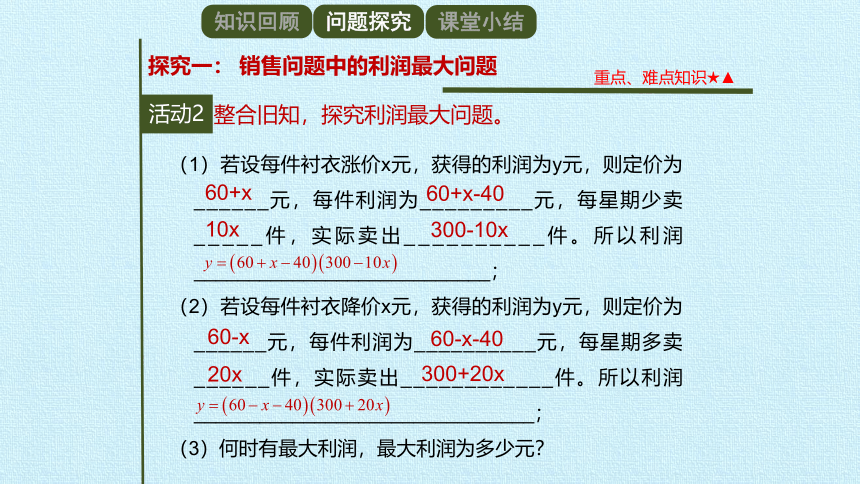
活动2
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
整合旧知,探究利润最大问题。
例1.小红的爸爸出售一批衬衣,这批衬衣现在的售价是60元每件,每星期可卖出300件,市场调查反映:如果调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件,已知该衬衣的进价为每件40元,如何定价才能使利润最大?
1.问题中的定价可能在现在售价的基础上涨价或降价,获取的利润会一样吗?
2.如果你是老板,你会怎样定价?
思考
知识回顾
问题探究
课堂小结
活动2
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
(1)若设每件衬衣涨价x元,获得的利润为y元,则定价为______元,每件利润为_________元,每星期少卖_____件,实际卖出__________件。所以利润___________________________;
(2)若设每件衬衣降价x元,获得的利润为y元,则定价为______元,每件利润为__________元,每星期多卖______件,实际卖出____________件。所以利润_______________________________;
(3)何时有最大利润,最大利润为多少元?
整合旧知,探究利润最大问题。
60+x
60+x-40
10x
300-10x
60-x
60-x-40
20x
300+20x
知识回顾
问题探究
课堂小结
活动2
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
例1.小红的爸爸出售一批衬衣,这批衬衣现在的售价是60元每件,每星期可卖出300件,市场调查反映:如果调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件,已知该衬衣的进价为每件40元,如何定价才能使利润最大?
整合旧知,探究利润最大问题。
解:涨价时:
当x=5时,取得最大值为6250元。
降价时:
当x=2.5时,取得最大值为6125元。
得出结论,当涨价5元时,取得的最大值为6250元。
知识回顾
问题探究
课堂小结
活动2
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
练习:小红的爸爸是个服装店老板,将进价为100元的服装按x元出售,每天可销售(200-x)件,若想获得最大利润,则x应定为( )
A.150元 B.160元 C.170元 D.180元
整合旧知,探究利润最大问题
【解题过程】最大利润y=(x-100) (200-x)=-(x-150)2+2500, 当x=150时,取得最大值。
A
【思路点拨】列出最大利润的关系式是本题关键。
知识回顾
问题探究
课堂小结
活动3
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
探究复杂问题中的利润最大问题
例2.某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元)。设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元。
(1)求y与x的函数关系式并直接写出自变量x的取值范围。
知识回顾
问题探究
课堂小结
解:y=(210-10x)(50+x-40)
=-10x2+110x+2100(0【思路点拨】
根据利润=每件利润×销售量,列出表达式即可,注意自变量范围;
活动3
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
探究复杂问题中的利润最大问题
例2.某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元)。设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元。
(2)每件商品的售价定为多少元时,所获月利润最大,最大月利润是多少元?
(3)每件商品的售价定为多少元时,月利润恰好是2200元?根据以上的结论,请你直接写出售价在什么范围时,月利润不低于2200元?
知识回顾
问题探究
课堂小结
【思路点拨】(2)求二次函数最值即可,注意自变量取整数;(3)列方程求解。
活动3
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
探究复杂问题中的利润最大问题
解:y=-10(x-5.5)2+2402.5,
∵a=-10<0,
∴当x=5.5时,y有最大值2402.5,
∵0当x=5时,50+x=55,y=2400(元),
当x=6时,50+x=56,y=2400(元),
∴当售价定为每件55或56元时,每个月的利润最大,最大的月利润是2400元;
知识回顾
问题探究
课堂小结
(2)每件商品的售价定为多少元时,所获月利润最大,最大月利润是多少元?
活动3
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
探究复杂问题中的利润最大问题
解:当y=2200时,-10x2+110x+2100=2200,
解得x1=1,x2=10,
∴当x=1时,50+x=51; 当x=10时,50+x=60,
∴当售价定为每件51或60元时,每个月的利润为2200元,
当售价不低于51元且不高于60元且为整数时,每个月的利润不低于2200元。
知识回顾
问题探究
课堂小结
(3)每件商品的售价定为多少元时,月利润恰好是2200元?根据以上的结论,请你直接写出售价在什么范围时,月利润不低于2200元?
活动3
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
探究复杂问题中的利润最大问题
练习:将进货价为70元/件的某种商品按零售价100元/件出售时每天能卖出20件,若这种商品的零售价在一定范围内每降价1元,其日销售量就增加1件。为了获得最大利润决定降价x元,则单件的利润为 元,每日的销售量为 件,每日的利润y= ,所以每件降价____元时,每日获得的利润最大为______元。
【思路点拨】能用未知数表示清楚销售问题中的各种关系。
(30-x)
(20+x)
(20+x)( 30-x)
625
5
知识回顾
问题探究
课堂小结
活动1
探究二:销售问题中的利润最大问题综合训练
基础性例题
例1.某经销店代销一种材料,当每吨售价为260元时,月销售量为45吨,该经销店为提高经营利润,准备采取降价的方式进行促销,经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7。5吨,每售出1吨建筑材料共需支付厂家及其他费用100元,设每吨材料售价为x(元),该经销店的月利润为y(元)。
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的函数关系式;(不要求写出x的取值范围)
(3)该经销店要获得最大月利润,售价应定为每吨多少元?
(4)王强说:“当月利润最大时,月销售额也最大。”你认为对吗?请说明理由。
知识回顾
问题探究
课堂小结
探究二:销售问题中的利润最大问题综合训练
知识回顾
问题探究
课堂小结
解:(1)
(3)
此经销店要获得最大月利润,材料的售价应定为每吨210元。
(2)
化简,得
(4)我认为,王强说得不对。
理由:当月利润最大时,x为210元,而月销售额为:
当x为160元时,月销售额W最大,
∴当x为210元时,月销售额W不是最大。∴王强说得不对。
探究二:销售问题中的利润最大问题综合训练
知识回顾
问题探究
课堂小结
【思路点拨】列出最大利润的关系式是本题的关键。
探究二:销售问题中的利润最大问题综合训练
练习:某网店销售某款童装,每件售价60元,每星期可卖300件。 为了促俏,该店决定降价销售,市场调查反映:每降价1元,每星期可多卖30件。 已知该款童装每件成本价40元。 设该款童装每件售价x元,每星期的销售量为y件。
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
知识回顾
问题探究
课堂小结
探究二:销售问题中的利润最大问题综合训练
知识回顾
问题探究
课堂小结
解:(1)y=300+30(60-x)=-30x+2100。
(2)设每星期的销售利润为W元,依题意,得
W=(x-40)(-30x+2100)=-30x2+3300x-84000
= -30(x-55)2+6750。
∵a= -30<0,
∴x=55时,W最大值=6750(元)。
即每件售价定为55元时,每星期的销售利润最大,最大利润是6750元。
探究二:销售问题中的利润最大问题综合训练
知识回顾
问题探究
课堂小结
(3)由题意,得:- 30(x-55)2+6750=6480。
解这个方程,得 x1=52,x2=58。
∵抛物线W= - 30(x-55)2+6750的开口向下,
∴当52≤x≤58时,每星期销售利润不低于6480元。
∴在y=- 30x+2100中,k=-30<0,y随x的增大而减小。
∴当x=58时,y最小值= - 30×58+2100=360。
即每星期至少要销售该款童装360件。
活动2
探究二:销售问题中的利润最大问题综合训练
提升型例题
例2.某商品进价为每件40元,售价为每件60元时,每个月可卖出100件;如果每件商品售价每上涨1元,则每个月少卖2件。设每件商品的售价为x元(x为正整数),每个月的销售利润为y元。
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,所获月利润最大,最大月利润是多少元?
(3)当售价的范围是多少时,使得每件商品的利润率不超过80%且每个月的利润不低于2250元?
知识回顾
问题探究
课堂小结
探究二:销售问题中的利润最大问题综合训练
解:(1)由题意解得:y= [100﹣2(x﹣60)](x﹣40)
=﹣2x2+300x﹣8800(60≤x≤110且x为正整数);
(2)y=﹣2(x﹣75)2+2450,当x=75时,y有最大值为2450元;
(3)当y=2250时,﹣2(x﹣75)2+2450=2250,
解得x1=65,x2=85,
∵a=﹣2<0,开口向下,当y≥2250时,65≤x≤85。
∵每件商品的利润率不超过80%,即 < 80%,
∴x≤72,故65≤x≤72。
答:当售价x的范围是65≤x≤72时,每件商品的利润率不超过80%且每个月的利润不低于2250元。
知识回顾
问题探究
课堂小结
探究二:销售问题中的利润最大问题综合训练
练习:东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为
且其日销售量y(kg)与时间t(天)的关系如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 时间t(天)
1
3
6
10
20
30
…
日销售量y(kg)
118
114
108
100
80
40
…
知识回顾
问题探究
课堂小结
探究二:销售问题中的利润最大问题综合训练
知识回顾
问题探究
课堂小结
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
解:依题意,设y=kt+b,
将(10,100),(20,80)代入y=kt+b,
解得:
∴日销售量y(kg)与时间t(天)的关系 y=120-2t。
当t=30时,y=120-60=60。
∴在第30天的日销售量为60千克。
探究二:销售问题中的利润最大问题综合训练
知识回顾
问题探究
课堂小结
(2)问哪一天的销售利润最大?最大日销售利润为多少?
解:设日销售利润为W元,则W=(p-20)y。
当1≤t≤24时,W
当t=10时,W最大=1250。
当25≤t≤48时,W
由二次函数的图象及性质知:
当t=25时,W最大=1085。
∵1250>1085,
∴在第10天的销售利润最大,最大利润为1250元。
探究二:销售问题中的利润最大问题综合训练
知识回顾
问题探究
课堂小结
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象。现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围。
解:设每天扣除捐赠后的日销售利润为m元。
由题意得m=
∵前24天,每天扣除捐赠后的日销售利润随时间t的增大而增大,
∴2n+10=24,∴n=7。
又∵n<9,
∴n的取值范围为7=n<9。
探究二:销售问题中的利润最大问题综合训练
【思路点拨】(1)根据日销售量y(kg)与时间t(天)的关系表,设y=kt+b,将表中对应数值代入即可求出k,b,从而求出一次函数关系式,再将t=30代入所求的一次函数关系式中,即可求出第30天的日销售量。
(2)日销售利润=日销售量×(销售单价-成本);分1≤t≤24和25≤t≤48两种情况,按照题目中所给出的销售单价p(元/kg)与时间t(天)之间的函数关系式分别得出销售利润的关系式,再运用二次函数的图象及性质即可得出结果。
(3)根据题意列出日销售利润函数,根据日销售利润随t的增大而增大,得n与t的关系,即可得出n的取值范围。
知识回顾
问题探究
课堂小结
活动3
探究二:销售问题中的利润最大问题综合训练
例3.一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg,且不高于180元/kg,经销一段时间后得到如下数据:
设y与x的关系是我们所学过的某一种函数关系。
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}销售单价x(元/kg)
120
130
…
180
每天销量y(kg)
100
95
…
70
探究型例题
知识回顾
问题探究
课堂小结
探究二:销售问题中的利润最大问题综合训练
解:(1)y=-0.5x+160(120≤x≤180)
知识回顾
问题探究
课堂小结
(2)设销售利润为W元,则
W=(x-80)(-0.5x+160)= ,
∵a= -<0,
∴当x<200时,y随x的增大而增大,
∴当x=180时, =7000,
则当销售单价为180元时,销售利润最大,最大利润是7000元。
【思路点拨】先列出销售利润的关系式,用关系式求最值;设销售利润为W元,则W=(x-80)(-0.5x+160)
结合二次函数图象和自变量取值范围,可确定x=180时,利润最大。
探究二:销售问题中的利润最大问题综合训练
练习:某蔬菜经销商到蔬菜种植基地采购一种蔬菜,经销商一次性采购蔬菜的采购单价y(元/千克)与采购量x(千克)之间的函数关系图象如图中折线AB——BC——CD所示(不包括端点A)。
(1)当100<x<200时,直接写y与x之间的函数关系式。
(2)蔬菜的种植成本为2元/千克,某经销商一次性采购蔬菜的采购量不超过200千克,当采购量是多少时,蔬菜种植基地获利最大,最大利润是多少元?
知识回顾
问题探究
课堂小结
探究二:销售问题中的利润最大问题综合训练
解:(1)设当100<x<200时,y与x之间的函数关系式为:y=ax+b,则
∴y与x之间的函数关系式为:y=-0.02x+8;
知识回顾
问题探究
课堂小结
解得:
【思路点拨】(1)利用待定系数法求出当100<x<200时,y与x之间的函数关系式即可;
探究二:销售问题中的利润最大问题综合训练
(2)当采购量是x千克时,蔬菜种植基地获利W元,
当0<x≤100时,W=(6-2)x=4x,
当x=100时,W有最大值400元,
当100<x≤200时,
W=(y-2)x =(-0.02x+6)x=-0.02(x-150)2+450,
∵当x=150时,W有最大值为450元,
综上所述,一次性采购量为150千克时,蔬菜种植基地能获得最大利润为450元。
知识回顾
问题探究
课堂小结
【思路点拨】(2)当0<x≤100时和100<x≤200时,分别求出获利W与x的函数关系式,进而求出最值即可。
知识梳理
知识回顾
问题探究
课堂小结
(2)利润=每件利润×销售量,
每件利润=每件售价﹣每件进价。
(3)建立函数关系,用函数的观点、思想分析解决实际问题。
(1)抛物线 的最值问题:
①若a>0,则当x= 时,y最小值= 。
②若a<0,则当x= 时,y最大值= 。
重难点突破
知识回顾
问题探究
课堂小结
(1)根据题意列出实际问题中变量之间的二次函数关系;
(2)运用二次函数的知识求出实际问题中的最值,有的是要在区间求最值;
(3)建立函数关系,用函数的观点、思想分析解决实际问题。
谢 谢
知识回顾
问题探究
课堂小结
(1)营销问题的基本等量关系:
利润=每件利润×销售量
每件利润=每件售价﹣每件进价。
(2)抛物线 的最值问题:
①若a>0,则当x= 时,y最小值= 。
②若a<0,则当x= 时,y最大值= 。
活动1
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
回顾旧知,回忆销售问题中常见概念和公式。
成本价;定价;售价;利润;销量;利润率;定价;
销售问题中一般都会涉及哪些名词?它们之间的数量关系是什么?
利润=每件利润×销售量
每件利润=每件售价﹣每件进价。
知识回顾
问题探究
课堂小结
活动2
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
整合旧知,探究利润最大问题。
例1.小红的爸爸出售一批衬衣,这批衬衣现在的售价是60元每件,每星期可卖出300件,市场调查反映:如果调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件,已知该衬衣的进价为每件40元,如何定价才能使利润最大?
1.问题中的定价可能在现在售价的基础上涨价或降价,获取的利润会一样吗?
2.如果你是老板,你会怎样定价?
思考
知识回顾
问题探究
课堂小结
活动2
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
(1)若设每件衬衣涨价x元,获得的利润为y元,则定价为______元,每件利润为_________元,每星期少卖_____件,实际卖出__________件。所以利润___________________________;
(2)若设每件衬衣降价x元,获得的利润为y元,则定价为______元,每件利润为__________元,每星期多卖______件,实际卖出____________件。所以利润_______________________________;
(3)何时有最大利润,最大利润为多少元?
整合旧知,探究利润最大问题。
60+x
60+x-40
10x
300-10x
60-x
60-x-40
20x
300+20x
知识回顾
问题探究
课堂小结
活动2
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
例1.小红的爸爸出售一批衬衣,这批衬衣现在的售价是60元每件,每星期可卖出300件,市场调查反映:如果调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件,已知该衬衣的进价为每件40元,如何定价才能使利润最大?
整合旧知,探究利润最大问题。
解:涨价时:
当x=5时,取得最大值为6250元。
降价时:
当x=2.5时,取得最大值为6125元。
得出结论,当涨价5元时,取得的最大值为6250元。
知识回顾
问题探究
课堂小结
活动2
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
练习:小红的爸爸是个服装店老板,将进价为100元的服装按x元出售,每天可销售(200-x)件,若想获得最大利润,则x应定为( )
A.150元 B.160元 C.170元 D.180元
整合旧知,探究利润最大问题
【解题过程】最大利润y=(x-100) (200-x)=-(x-150)2+2500, 当x=150时,取得最大值。
A
【思路点拨】列出最大利润的关系式是本题关键。
知识回顾
问题探究
课堂小结
活动3
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
探究复杂问题中的利润最大问题
例2.某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元)。设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元。
(1)求y与x的函数关系式并直接写出自变量x的取值范围。
知识回顾
问题探究
课堂小结
解:y=(210-10x)(50+x-40)
=-10x2+110x+2100(0
根据利润=每件利润×销售量,列出表达式即可,注意自变量范围;
活动3
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
探究复杂问题中的利润最大问题
例2.某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元)。设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元。
(2)每件商品的售价定为多少元时,所获月利润最大,最大月利润是多少元?
(3)每件商品的售价定为多少元时,月利润恰好是2200元?根据以上的结论,请你直接写出售价在什么范围时,月利润不低于2200元?
知识回顾
问题探究
课堂小结
【思路点拨】(2)求二次函数最值即可,注意自变量取整数;(3)列方程求解。
活动3
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
探究复杂问题中的利润最大问题
解:y=-10(x-5.5)2+2402.5,
∵a=-10<0,
∴当x=5.5时,y有最大值2402.5,
∵0
当x=6时,50+x=56,y=2400(元),
∴当售价定为每件55或56元时,每个月的利润最大,最大的月利润是2400元;
知识回顾
问题探究
课堂小结
(2)每件商品的售价定为多少元时,所获月利润最大,最大月利润是多少元?
活动3
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
探究复杂问题中的利润最大问题
解:当y=2200时,-10x2+110x+2100=2200,
解得x1=1,x2=10,
∴当x=1时,50+x=51; 当x=10时,50+x=60,
∴当售价定为每件51或60元时,每个月的利润为2200元,
当售价不低于51元且不高于60元且为整数时,每个月的利润不低于2200元。
知识回顾
问题探究
课堂小结
(3)每件商品的售价定为多少元时,月利润恰好是2200元?根据以上的结论,请你直接写出售价在什么范围时,月利润不低于2200元?
活动3
重点、难点知识★▲
探究一: 销售问题中的利润最大问题
探究复杂问题中的利润最大问题
练习:将进货价为70元/件的某种商品按零售价100元/件出售时每天能卖出20件,若这种商品的零售价在一定范围内每降价1元,其日销售量就增加1件。为了获得最大利润决定降价x元,则单件的利润为 元,每日的销售量为 件,每日的利润y= ,所以每件降价____元时,每日获得的利润最大为______元。
【思路点拨】能用未知数表示清楚销售问题中的各种关系。
(30-x)
(20+x)
(20+x)( 30-x)
625
5
知识回顾
问题探究
课堂小结
活动1
探究二:销售问题中的利润最大问题综合训练
基础性例题
例1.某经销店代销一种材料,当每吨售价为260元时,月销售量为45吨,该经销店为提高经营利润,准备采取降价的方式进行促销,经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7。5吨,每售出1吨建筑材料共需支付厂家及其他费用100元,设每吨材料售价为x(元),该经销店的月利润为y(元)。
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的函数关系式;(不要求写出x的取值范围)
(3)该经销店要获得最大月利润,售价应定为每吨多少元?
(4)王强说:“当月利润最大时,月销售额也最大。”你认为对吗?请说明理由。
知识回顾
问题探究
课堂小结
探究二:销售问题中的利润最大问题综合训练
知识回顾
问题探究
课堂小结
解:(1)
(3)
此经销店要获得最大月利润,材料的售价应定为每吨210元。
(2)
化简,得
(4)我认为,王强说得不对。
理由:当月利润最大时,x为210元,而月销售额为:
当x为160元时,月销售额W最大,
∴当x为210元时,月销售额W不是最大。∴王强说得不对。
探究二:销售问题中的利润最大问题综合训练
知识回顾
问题探究
课堂小结
【思路点拨】列出最大利润的关系式是本题的关键。
探究二:销售问题中的利润最大问题综合训练
练习:某网店销售某款童装,每件售价60元,每星期可卖300件。 为了促俏,该店决定降价销售,市场调查反映:每降价1元,每星期可多卖30件。 已知该款童装每件成本价40元。 设该款童装每件售价x元,每星期的销售量为y件。
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
知识回顾
问题探究
课堂小结
探究二:销售问题中的利润最大问题综合训练
知识回顾
问题探究
课堂小结
解:(1)y=300+30(60-x)=-30x+2100。
(2)设每星期的销售利润为W元,依题意,得
W=(x-40)(-30x+2100)=-30x2+3300x-84000
= -30(x-55)2+6750。
∵a= -30<0,
∴x=55时,W最大值=6750(元)。
即每件售价定为55元时,每星期的销售利润最大,最大利润是6750元。
探究二:销售问题中的利润最大问题综合训练
知识回顾
问题探究
课堂小结
(3)由题意,得:- 30(x-55)2+6750=6480。
解这个方程,得 x1=52,x2=58。
∵抛物线W= - 30(x-55)2+6750的开口向下,
∴当52≤x≤58时,每星期销售利润不低于6480元。
∴在y=- 30x+2100中,k=-30<0,y随x的增大而减小。
∴当x=58时,y最小值= - 30×58+2100=360。
即每星期至少要销售该款童装360件。
活动2
探究二:销售问题中的利润最大问题综合训练
提升型例题
例2.某商品进价为每件40元,售价为每件60元时,每个月可卖出100件;如果每件商品售价每上涨1元,则每个月少卖2件。设每件商品的售价为x元(x为正整数),每个月的销售利润为y元。
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,所获月利润最大,最大月利润是多少元?
(3)当售价的范围是多少时,使得每件商品的利润率不超过80%且每个月的利润不低于2250元?
知识回顾
问题探究
课堂小结
探究二:销售问题中的利润最大问题综合训练
解:(1)由题意解得:y= [100﹣2(x﹣60)](x﹣40)
=﹣2x2+300x﹣8800(60≤x≤110且x为正整数);
(2)y=﹣2(x﹣75)2+2450,当x=75时,y有最大值为2450元;
(3)当y=2250时,﹣2(x﹣75)2+2450=2250,
解得x1=65,x2=85,
∵a=﹣2<0,开口向下,当y≥2250时,65≤x≤85。
∵每件商品的利润率不超过80%,即 < 80%,
∴x≤72,故65≤x≤72。
答:当售价x的范围是65≤x≤72时,每件商品的利润率不超过80%且每个月的利润不低于2250元。
知识回顾
问题探究
课堂小结
探究二:销售问题中的利润最大问题综合训练
练习:东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为
且其日销售量y(kg)与时间t(天)的关系如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 时间t(天)
1
3
6
10
20
30
…
日销售量y(kg)
118
114
108
100
80
40
…
知识回顾
问题探究
课堂小结
探究二:销售问题中的利润最大问题综合训练
知识回顾
问题探究
课堂小结
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
解:依题意,设y=kt+b,
将(10,100),(20,80)代入y=kt+b,
解得:
∴日销售量y(kg)与时间t(天)的关系 y=120-2t。
当t=30时,y=120-60=60。
∴在第30天的日销售量为60千克。
探究二:销售问题中的利润最大问题综合训练
知识回顾
问题探究
课堂小结
(2)问哪一天的销售利润最大?最大日销售利润为多少?
解:设日销售利润为W元,则W=(p-20)y。
当1≤t≤24时,W
当t=10时,W最大=1250。
当25≤t≤48时,W
由二次函数的图象及性质知:
当t=25时,W最大=1085。
∵1250>1085,
∴在第10天的销售利润最大,最大利润为1250元。
探究二:销售问题中的利润最大问题综合训练
知识回顾
问题探究
课堂小结
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象。现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围。
解:设每天扣除捐赠后的日销售利润为m元。
由题意得m=
∵前24天,每天扣除捐赠后的日销售利润随时间t的增大而增大,
∴2n+10=24,∴n=7。
又∵n<9,
∴n的取值范围为7=n<9。
探究二:销售问题中的利润最大问题综合训练
【思路点拨】(1)根据日销售量y(kg)与时间t(天)的关系表,设y=kt+b,将表中对应数值代入即可求出k,b,从而求出一次函数关系式,再将t=30代入所求的一次函数关系式中,即可求出第30天的日销售量。
(2)日销售利润=日销售量×(销售单价-成本);分1≤t≤24和25≤t≤48两种情况,按照题目中所给出的销售单价p(元/kg)与时间t(天)之间的函数关系式分别得出销售利润的关系式,再运用二次函数的图象及性质即可得出结果。
(3)根据题意列出日销售利润函数,根据日销售利润随t的增大而增大,得n与t的关系,即可得出n的取值范围。
知识回顾
问题探究
课堂小结
活动3
探究二:销售问题中的利润最大问题综合训练
例3.一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg,且不高于180元/kg,经销一段时间后得到如下数据:
设y与x的关系是我们所学过的某一种函数关系。
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}销售单价x(元/kg)
120
130
…
180
每天销量y(kg)
100
95
…
70
探究型例题
知识回顾
问题探究
课堂小结
探究二:销售问题中的利润最大问题综合训练
解:(1)y=-0.5x+160(120≤x≤180)
知识回顾
问题探究
课堂小结
(2)设销售利润为W元,则
W=(x-80)(-0.5x+160)= ,
∵a= -<0,
∴当x<200时,y随x的增大而增大,
∴当x=180时, =7000,
则当销售单价为180元时,销售利润最大,最大利润是7000元。
【思路点拨】先列出销售利润的关系式,用关系式求最值;设销售利润为W元,则W=(x-80)(-0.5x+160)
结合二次函数图象和自变量取值范围,可确定x=180时,利润最大。
探究二:销售问题中的利润最大问题综合训练
练习:某蔬菜经销商到蔬菜种植基地采购一种蔬菜,经销商一次性采购蔬菜的采购单价y(元/千克)与采购量x(千克)之间的函数关系图象如图中折线AB——BC——CD所示(不包括端点A)。
(1)当100<x<200时,直接写y与x之间的函数关系式。
(2)蔬菜的种植成本为2元/千克,某经销商一次性采购蔬菜的采购量不超过200千克,当采购量是多少时,蔬菜种植基地获利最大,最大利润是多少元?
知识回顾
问题探究
课堂小结
探究二:销售问题中的利润最大问题综合训练
解:(1)设当100<x<200时,y与x之间的函数关系式为:y=ax+b,则
∴y与x之间的函数关系式为:y=-0.02x+8;
知识回顾
问题探究
课堂小结
解得:
【思路点拨】(1)利用待定系数法求出当100<x<200时,y与x之间的函数关系式即可;
探究二:销售问题中的利润最大问题综合训练
(2)当采购量是x千克时,蔬菜种植基地获利W元,
当0<x≤100时,W=(6-2)x=4x,
当x=100时,W有最大值400元,
当100<x≤200时,
W=(y-2)x =(-0.02x+6)x=-0.02(x-150)2+450,
∵当x=150时,W有最大值为450元,
综上所述,一次性采购量为150千克时,蔬菜种植基地能获得最大利润为450元。
知识回顾
问题探究
课堂小结
【思路点拨】(2)当0<x≤100时和100<x≤200时,分别求出获利W与x的函数关系式,进而求出最值即可。
知识梳理
知识回顾
问题探究
课堂小结
(2)利润=每件利润×销售量,
每件利润=每件售价﹣每件进价。
(3)建立函数关系,用函数的观点、思想分析解决实际问题。
(1)抛物线 的最值问题:
①若a>0,则当x= 时,y最小值= 。
②若a<0,则当x= 时,y最大值= 。
重难点突破
知识回顾
问题探究
课堂小结
(1)根据题意列出实际问题中变量之间的二次函数关系;
(2)运用二次函数的知识求出实际问题中的最值,有的是要在区间求最值;
(3)建立函数关系,用函数的观点、思想分析解决实际问题。
谢 谢
同课章节目录
