苏科版八年级上册 第一章《全等三角形》中的运动类问题特优生专练(1)(Word版 含解析)
文档属性
| 名称 | 苏科版八年级上册 第一章《全等三角形》中的运动类问题特优生专练(1)(Word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 326.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-11 00:00:00 | ||
图片预览


文档简介
2020苏科版八上第一章《全等三角形》中的运动类问题特优生专练(1)
班级:___________姓名:___________得分:___________
一、解答题
如图,已知中,,厘米,厘米,点D为AB的中点.如果点P在线段BC上以每秒4厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为秒.
用的代数式表示PC的长度;
若点P、Q的运动速度相等,经过1秒后,与是否全等,请说明理由;
若点P、Q的运动速度不相等,当点Q的运动速度a为多少时,能够使与全等?
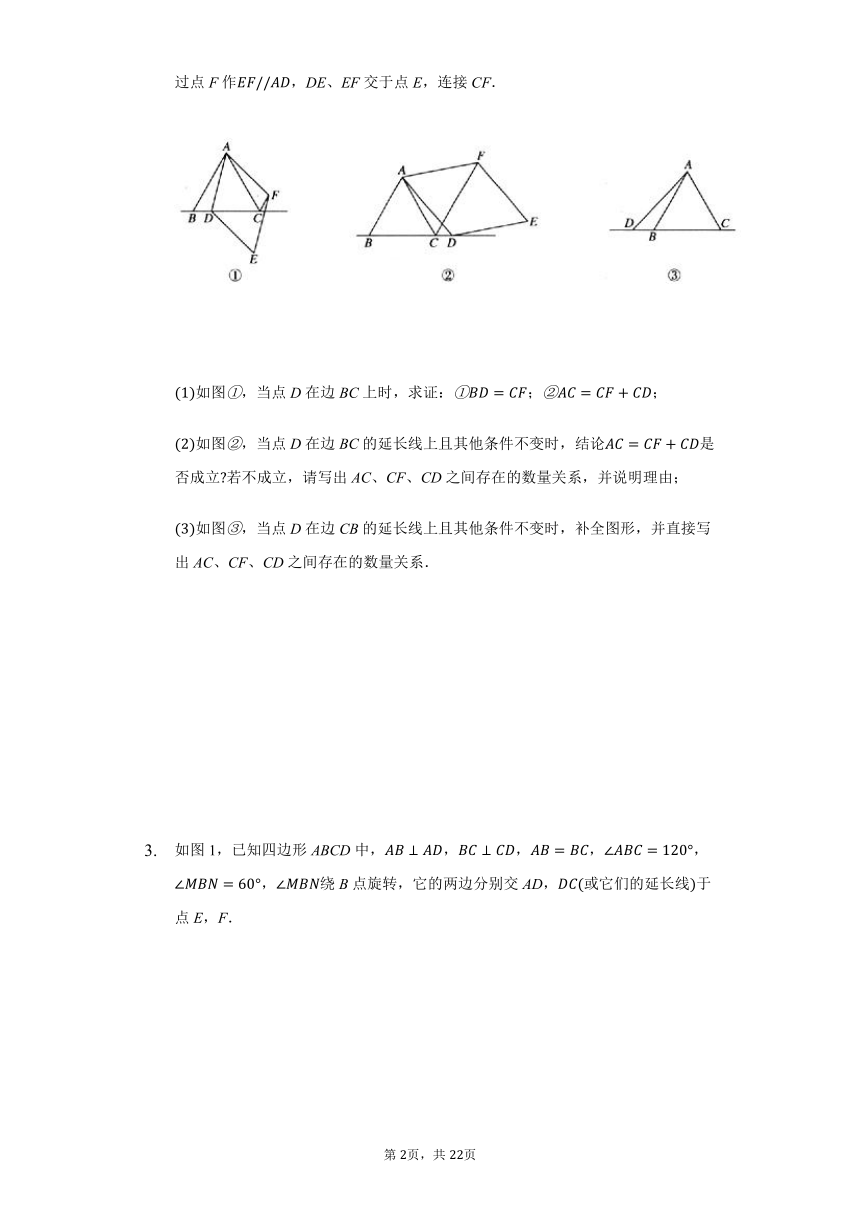
已知为等边三角形,点D为直线BC上的一动点点D不与点B、C重合,以AD为边作,在射线AF上截取点F,使,过点D作,过点F作,DE、EF交于点E,连接CF.
如图,当点D在边BC上时,求证:;;
如图,当点D在边BC的延长线上且其他条件不变时,结论是否成立若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;
如图,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.
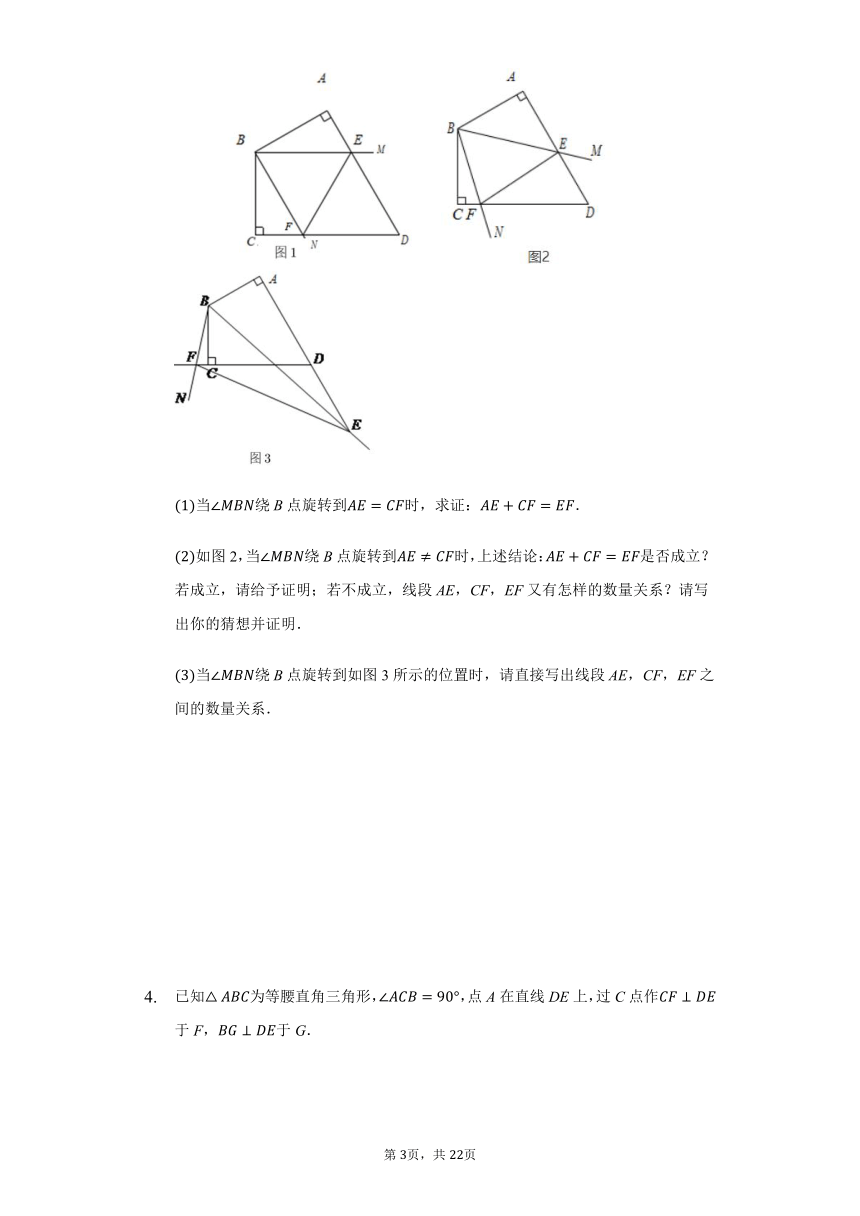
如图1,已知四边形ABCD中,,,,,,绕B点旋转,它的两边分别交AD,或它们的延长线于点E,F.
?
?
??
?
当绕B点旋转到时,求证:.
如图2,当绕B点旋转到时,上述结论:是否成立?若成立,请给予证明;若不成立,线段AE,CF,EF又有怎样的数量关系?请写出你的猜想并证明.
当绕B点旋转到如图3所示的位置时,请直接写出线段AE,CF,EF之间的数量关系.
已知为等腰直角三角形,,点A在直线DE上,过C点作于F,于G.
发现问题:如图1,当B、C两点均在直线DE上方时,线段AG、BG和CF存在的数量关系是________;
类比探究:当绕点A顺时针旋转至图2的位置时,线段AG、BG和CF之间的数量关系是否会发生变化如果不变,请说明理由;如果变化、请写出你的猜想,并给予证明;
拓展延伸:当绕点A顺时针旋转至图3的位置时,若,,请直接写出的面积.
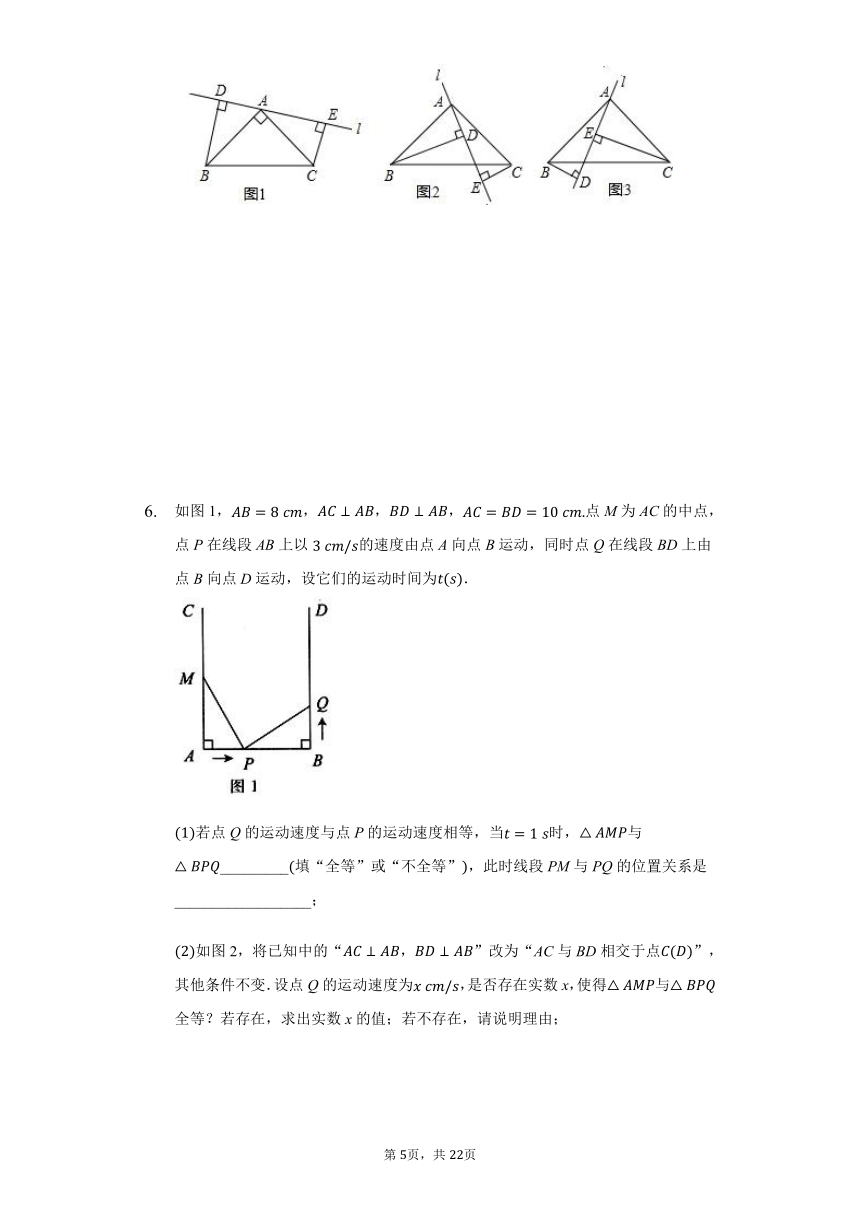
在中,,,l是过A的一条直线,于D,于求证:
当直线l绕点A旋转到如图1位置时,试说明:.
若直线l绕点A旋转到如图2位置时,试说明:.
若直线l绕点A旋转到如图3位置时,试问:BD与DE,CE具有怎样的等量关系?请写出结果,不必证明.
如图1,,,,点M为AC的中点,点P在线段AB上以的速度由点A向点B运动,同时点Q在线段BD上由点B向点D运动,设它们的运动时间为.
若点Q的运动速度与点P的运动速度相等,当时,与_________填“全等”或“不全等”,此时线段PM与PQ的位置关系是__________________;
如图2,将已知中的“,”改为“AC与BD相交于点”,其他条件不变.设点Q的运动速度为,是否存在实数x,使得与全等?若存在,求出实数x的值;若不存在,请说明理由;
如图3,点Q以中的速度从点B出发,同时点P以原来的速度从点A出发,都按逆时针沿的三边运动.直
接写出点P与点Q第一次相遇时,两个点所在三角形的边和所经过的时间.
已知等腰三角形ABC中,,点E在AC边的延长线上,点D在直线BC上,且,点M,N分别是DE,AE的中点,连接MN,交直线BE与点当点D在边CB的延长线上时,如图1所示,易证.
当点D在CB边上时,如图2所示,上述结论是否成立?若成立,请给出证明;若不成立,请写出关于线段MF、FN与BE之间关系的结论,并说明理由.
当点D在BC边的延长线上时,如图3所示,分析MF、FN与BE的关系,请直接写出你的结论不需要的证明
如图1,,,,点P在线段AB上以的速度由A向B运动同时点Q在线段BD上由点B向点D运动它们运动的时间为.
若点Q的运动速度与点P的运动速度相等,当时,与是否全等?请说明理由,并判断此时线段PC和线段PQ的位置关系.
如图2,将“,”改为“”,其他条件不变,设点Q运动速度为,是否存在实数x,使得与全等?若存在,求出相应x,t的值;若不存在,说明理由.
判断与说理
如图1,中,且,,EC、DB分别平分、,交AD、AE于点C、B,连接请你判断AB、AC是否相等,并说明理由;
的位置保持不变,将绕点A逆时针旋转至图2的位置,AD、BE相交于O,请你判断线段BE与CD的关系,并说明理由.
已知≌,.
如图,当C、A、D在同一直线上时,连CE、BD,判断CE和BD的位置关系,填空:CE_____BD.
如图,把绕点A旋转到如图所示的位置,试问中的结论是否仍然成立,写出你的结论,并说明理由.
如图,在图的基础上,将绕点A旋转一个角度到如图所示的的位置,连接、,过点A作于点N,反向延长AN交于点求的值.
答案和解析
解:;
经过1秒后,与全等.
,点D为AB的中点,
,
经过1秒后,,
,,
,
,
在和中,
,
≌;
点P、Q的运动速度不相等时,与全等,则,
即秒,
,点D为AB的中点,
,
则,
点Q的运动速度,
当点Q的运动速度a为厘米秒时,与全等.
2.
证明:是等边三角形,,?
,,
,?
即.
?
在和中,
?
≌,
,
,?
即,;
?
解:不成立,AC、CF、CD之间存在的数量关系是.
理由如下:?
由知:,,,?
,即.
?
在和中,
?
≌,
,
,即;
?
解:补全图形如图,此时理由如下:
?
,
?
在和中,
?
≌,
,
,?
即.
3.
证明:和中,,,
≌,,
,
,,
,是等边三角形,
,,
;
如图2,将顺时针旋转,
,,
点与C点重合,
,,
,,,
,
在和中,
,
≌,
,
;
不成立,新结论为.
理由:如图3,将顺时针旋转,
,,
点与C点重合,,
,,
,
,
,
,
在和中,
,
≌,
,
.
4.
解:;
变化,猜想:.
证明:过C点作于H,
,
;
,四边形CFGH为矩形,
又为等腰直角三角形,,
,
,
,
四边形CFGH为正方形,
,;
的面积是5.
证明:如图,过点C做,交GB的延长线于点K,
,
,
,
四边形CFGK为矩形,
,
又,
,
即,
又为等腰直角三角形,
,
在和中,
≌,
,,
又四边形CFGK为矩形,
四边形CFGK为正方形,
,
;
见答案;
如图3,过点C做于点H,
可得,
,
≌,
,,
四边形CFGH是正方形,
,
,
,
,
,,
,,
的面积的面积梯形CFGB的面积的面积
.
5.
证明:如图1,,,
,
.
,
,
.
在和中,
,
≌,
,.
,
;
如图2,,,
,
.
,
,
.
在和中,
,
≌,
,
,
.
如图3,,,
,
.
,
,
.
在和中,
,
≌,
,
,
.
6.
解:全等,互相垂直;
存在实数x,使得与全等,
由题意,可知,,,.
,
.
当,时,≌,即,
,此时符合题意
当,时,≌,即,
,
,,即符合题意
综上所述,实数x为3或时,与全等
,则只可能Q点追上P点,
,即点Q比点P多走的路程,
设经过t秒Q追上P,则有
,
解得,
经过秒,P点走过的位移为,
在AC边第一次相遇.
点P,Q在出发时在AC边上第一次相遇。
解:点M为AC的中点,
,
,,
,,
,,
,
≌,
,
,
,
,
;
故答案为全等,互相垂直;
7.
证明:答:不成立,?
,?
理由如下:?
证明:如图2,连接AD,?
、N分别是DE、AE的中点,?
,?
又在与中,?
,?
≌,?
,?
,?
;?
图3结论:,?
证明:如图3,连接AD,
?
、N分别是DE、AE的中点,?
,?
在与中,?
,?
≌,?
,?
,?
,?
.
8.
解:当时,,,
又,
在和中,
≌.
,
,
,
即线段PC与线段PQ垂直;
若≌,
则,,
所以,
解得;
若≌,
则,,
,
解得;
综上所述,存在或使得与全等.
9.
解:
说理如下:平分,DB平分,
,,
,
,
在和中,
,,,
≌
;
,
,
,
,
在和中,,
≌,
,,
,
,
,
得,,
,
综上可得:,且.
10.
解:.
延长CE交BD于M,设AB与EM交于点F,
,
,
又≌,
,,
,,
,
又,,
,
,
;
过作于G,过D作交延长线于点H.
,
,,
,
,
≌,
,
同理可证≌,,
,
在与中,
,,,
≌,
,
.
第2页,共2页
第1页,共1页
班级:___________姓名:___________得分:___________
一、解答题
如图,已知中,,厘米,厘米,点D为AB的中点.如果点P在线段BC上以每秒4厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为秒.
用的代数式表示PC的长度;
若点P、Q的运动速度相等,经过1秒后,与是否全等,请说明理由;
若点P、Q的运动速度不相等,当点Q的运动速度a为多少时,能够使与全等?
已知为等边三角形,点D为直线BC上的一动点点D不与点B、C重合,以AD为边作,在射线AF上截取点F,使,过点D作,过点F作,DE、EF交于点E,连接CF.
如图,当点D在边BC上时,求证:;;
如图,当点D在边BC的延长线上且其他条件不变时,结论是否成立若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;
如图,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.
如图1,已知四边形ABCD中,,,,,,绕B点旋转,它的两边分别交AD,或它们的延长线于点E,F.
?
?
??
?
当绕B点旋转到时,求证:.
如图2,当绕B点旋转到时,上述结论:是否成立?若成立,请给予证明;若不成立,线段AE,CF,EF又有怎样的数量关系?请写出你的猜想并证明.
当绕B点旋转到如图3所示的位置时,请直接写出线段AE,CF,EF之间的数量关系.
已知为等腰直角三角形,,点A在直线DE上,过C点作于F,于G.
发现问题:如图1,当B、C两点均在直线DE上方时,线段AG、BG和CF存在的数量关系是________;
类比探究:当绕点A顺时针旋转至图2的位置时,线段AG、BG和CF之间的数量关系是否会发生变化如果不变,请说明理由;如果变化、请写出你的猜想,并给予证明;
拓展延伸:当绕点A顺时针旋转至图3的位置时,若,,请直接写出的面积.
在中,,,l是过A的一条直线,于D,于求证:
当直线l绕点A旋转到如图1位置时,试说明:.
若直线l绕点A旋转到如图2位置时,试说明:.
若直线l绕点A旋转到如图3位置时,试问:BD与DE,CE具有怎样的等量关系?请写出结果,不必证明.
如图1,,,,点M为AC的中点,点P在线段AB上以的速度由点A向点B运动,同时点Q在线段BD上由点B向点D运动,设它们的运动时间为.
若点Q的运动速度与点P的运动速度相等,当时,与_________填“全等”或“不全等”,此时线段PM与PQ的位置关系是__________________;
如图2,将已知中的“,”改为“AC与BD相交于点”,其他条件不变.设点Q的运动速度为,是否存在实数x,使得与全等?若存在,求出实数x的值;若不存在,请说明理由;
如图3,点Q以中的速度从点B出发,同时点P以原来的速度从点A出发,都按逆时针沿的三边运动.直
接写出点P与点Q第一次相遇时,两个点所在三角形的边和所经过的时间.
已知等腰三角形ABC中,,点E在AC边的延长线上,点D在直线BC上,且,点M,N分别是DE,AE的中点,连接MN,交直线BE与点当点D在边CB的延长线上时,如图1所示,易证.
当点D在CB边上时,如图2所示,上述结论是否成立?若成立,请给出证明;若不成立,请写出关于线段MF、FN与BE之间关系的结论,并说明理由.
当点D在BC边的延长线上时,如图3所示,分析MF、FN与BE的关系,请直接写出你的结论不需要的证明
如图1,,,,点P在线段AB上以的速度由A向B运动同时点Q在线段BD上由点B向点D运动它们运动的时间为.
若点Q的运动速度与点P的运动速度相等,当时,与是否全等?请说明理由,并判断此时线段PC和线段PQ的位置关系.
如图2,将“,”改为“”,其他条件不变,设点Q运动速度为,是否存在实数x,使得与全等?若存在,求出相应x,t的值;若不存在,说明理由.
判断与说理
如图1,中,且,,EC、DB分别平分、,交AD、AE于点C、B,连接请你判断AB、AC是否相等,并说明理由;
的位置保持不变,将绕点A逆时针旋转至图2的位置,AD、BE相交于O,请你判断线段BE与CD的关系,并说明理由.
已知≌,.
如图,当C、A、D在同一直线上时,连CE、BD,判断CE和BD的位置关系,填空:CE_____BD.
如图,把绕点A旋转到如图所示的位置,试问中的结论是否仍然成立,写出你的结论,并说明理由.
如图,在图的基础上,将绕点A旋转一个角度到如图所示的的位置,连接、,过点A作于点N,反向延长AN交于点求的值.
答案和解析
解:;
经过1秒后,与全等.
,点D为AB的中点,
,
经过1秒后,,
,,
,
,
在和中,
,
≌;
点P、Q的运动速度不相等时,与全等,则,
即秒,
,点D为AB的中点,
,
则,
点Q的运动速度,
当点Q的运动速度a为厘米秒时,与全等.
2.
证明:是等边三角形,,?
,,
,?
即.
?
在和中,
?
≌,
,
,?
即,;
?
解:不成立,AC、CF、CD之间存在的数量关系是.
理由如下:?
由知:,,,?
,即.
?
在和中,
?
≌,
,
,即;
?
解:补全图形如图,此时理由如下:
?
,
?
在和中,
?
≌,
,
,?
即.
3.
证明:和中,,,
≌,,
,
,,
,是等边三角形,
,,
;
如图2,将顺时针旋转,
,,
点与C点重合,
,,
,,,
,
在和中,
,
≌,
,
;
不成立,新结论为.
理由:如图3,将顺时针旋转,
,,
点与C点重合,,
,,
,
,
,
,
在和中,
,
≌,
,
.
4.
解:;
变化,猜想:.
证明:过C点作于H,
,
;
,四边形CFGH为矩形,
又为等腰直角三角形,,
,
,
,
四边形CFGH为正方形,
,;
的面积是5.
证明:如图,过点C做,交GB的延长线于点K,
,
,
,
四边形CFGK为矩形,
,
又,
,
即,
又为等腰直角三角形,
,
在和中,
≌,
,,
又四边形CFGK为矩形,
四边形CFGK为正方形,
,
;
见答案;
如图3,过点C做于点H,
可得,
,
≌,
,,
四边形CFGH是正方形,
,
,
,
,
,,
,,
的面积的面积梯形CFGB的面积的面积
.
5.
证明:如图1,,,
,
.
,
,
.
在和中,
,
≌,
,.
,
;
如图2,,,
,
.
,
,
.
在和中,
,
≌,
,
,
.
如图3,,,
,
.
,
,
.
在和中,
,
≌,
,
,
.
6.
解:全等,互相垂直;
存在实数x,使得与全等,
由题意,可知,,,.
,
.
当,时,≌,即,
,此时符合题意
当,时,≌,即,
,
,,即符合题意
综上所述,实数x为3或时,与全等
,则只可能Q点追上P点,
,即点Q比点P多走的路程,
设经过t秒Q追上P,则有
,
解得,
经过秒,P点走过的位移为,
在AC边第一次相遇.
点P,Q在出发时在AC边上第一次相遇。
解:点M为AC的中点,
,
,,
,,
,,
,
≌,
,
,
,
,
;
故答案为全等,互相垂直;
7.
证明:答:不成立,?
,?
理由如下:?
证明:如图2,连接AD,?
、N分别是DE、AE的中点,?
,?
又在与中,?
,?
≌,?
,?
,?
;?
图3结论:,?
证明:如图3,连接AD,
?
、N分别是DE、AE的中点,?
,?
在与中,?
,?
≌,?
,?
,?
,?
.
8.
解:当时,,,
又,
在和中,
≌.
,
,
,
即线段PC与线段PQ垂直;
若≌,
则,,
所以,
解得;
若≌,
则,,
,
解得;
综上所述,存在或使得与全等.
9.
解:
说理如下:平分,DB平分,
,,
,
,
在和中,
,,,
≌
;
,
,
,
,
在和中,,
≌,
,,
,
,
,
得,,
,
综上可得:,且.
10.
解:.
延长CE交BD于M,设AB与EM交于点F,
,
,
又≌,
,,
,,
,
又,,
,
,
;
过作于G,过D作交延长线于点H.
,
,,
,
,
≌,
,
同理可证≌,,
,
在与中,
,,,
≌,
,
.
第2页,共2页
第1页,共1页
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
