北师大版九年级上册数学 4.4探索三角形相似的条件 同步练习(Word版 含答案)
文档属性
| 名称 | 北师大版九年级上册数学 4.4探索三角形相似的条件 同步练习(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 109.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-11 11:15:10 | ||
图片预览


文档简介
4.4探索三角形相似的条件 同步练习
一.选择题
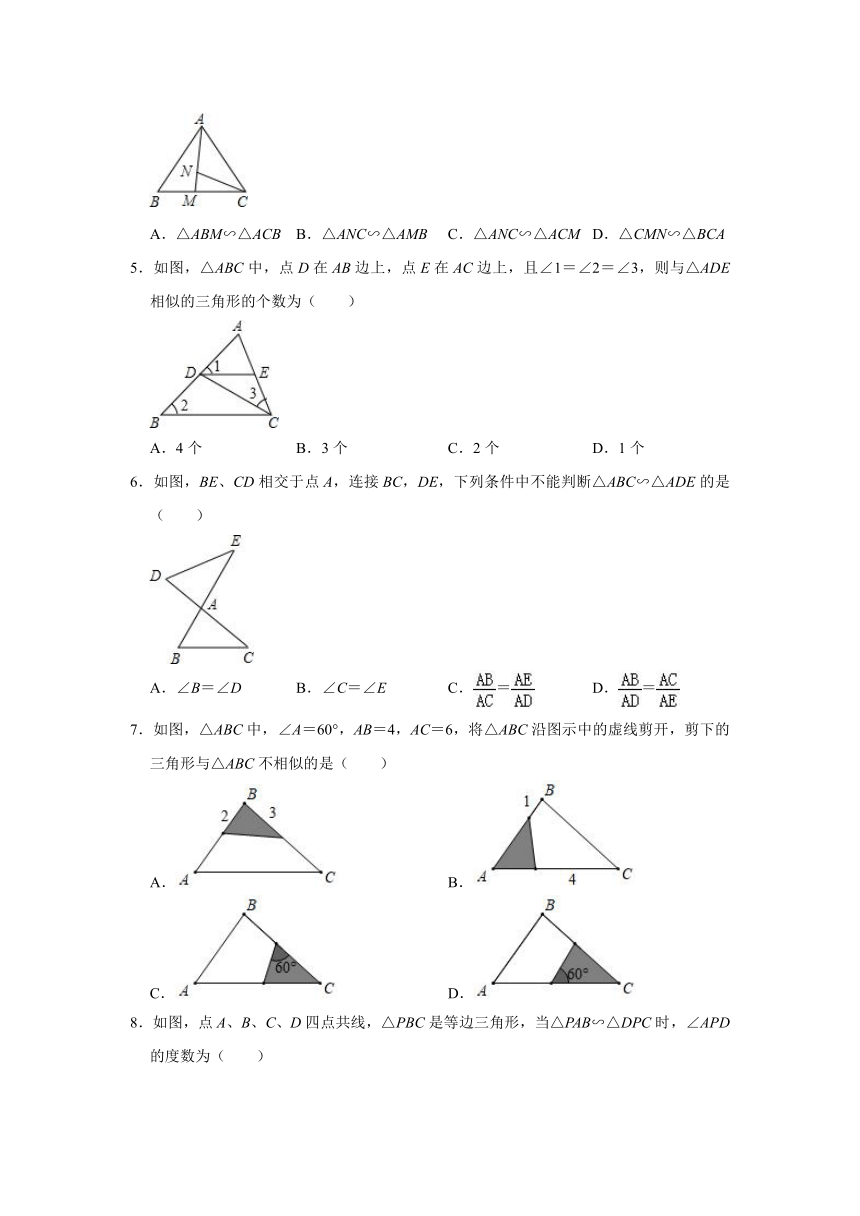
1.如图,已知在△ABC中,P为AB上一点,连接CP,以下条件中不能判定△ACP∽△ABC的是( )
A.∠ACP=∠B B.∠APC=∠ACB C. D.
2.下列正方形方格中四个三角形中,与甲图中的三角形相似的是( )
A. B.
C. D.
3.下列说法正确的是( )
A.所有等边三角形都相似
B.有一个角相等的两个等腰三角形相似
C.所有直角三角形都相似
D.所有矩形都相似
4.如图,点M在BC上,点N在AM上,CM=CN,,下列结论正确的是( )
A.△ABM∽△ACB B.△ANC∽△AMB C.△ANC∽△ACM D.△CMN∽△BCA
5.如图,△ABC中,点D在AB边上,点E在AC边上,且∠1=∠2=∠3,则与△ADE相似的三角形的个数为( )
A.4个 B.3个 C.2个 D.1个
6.如图,BE、CD相交于点A,连接BC,DE,下列条件中不能判断△ABC∽△ADE的是( )
A.∠B=∠D B.∠C=∠E C.= D.=
7.如图,△ABC中,∠A=60°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的三角形与△ABC不相似的是( )
A. B.
C. D.
8.如图,点A、B、C、D四点共线,△PBC是等边三角形,当△PAB∽△DPC时,∠APD的度数为( )
A.120° B.100° C.110° D.125°
9.在△ABC中,D、E分别在AB、AC上,给出下列条件:其中能判断△ADE∽△ABC的有( )
①;
②∠AED=∠B;
③;
④DE∥BC,
A.1个 B.2个 C.3个 D.4个
10.如图,在矩形ABCD中,点E,F分别在BC,CD边上,EF⊥AE,BH⊥AC于点H,EF与AC交于点M,BH与AE交于点N.则下列结论错误的是( )
A.△EFC∽△AEB B.△ECM∽△ABN C.△CFM∽△BEN D.△ANH∽△EFC
二.填空题
11.在△ABC中,AB=10,AC=5,点M在边AB上,且AM=2,点N在AC边上.当AN= 时,△AMN与原三角形相似.
12.如图,AB⊥BD,CD⊥BD,AB=6,CD=4,BD=14.点P在BD上移动,当以P,C,D为顶点的三角形与△ABP相似时,则PB的长为 .
13.如图,∠DAB=∠EAC,请补充一个条件: ,使△ADE∽△ABC(只写一个答案即可).
14.如图,矩形ABCD,AD=2,AB=5,P为CD边上的动点,当DP= 时,△ADP与△BCP相似.
15.如图,四边形ABCD中,∠A=∠B=90°,AB=5cm,AD=3cm,BC=2cm,P是AB上一点,若以P、A、D为顶点的三角形与△PBC相似,则PA= cm.
三.解答题
16.如图,D是△ABC的边AB上的一点,BD=2,AB=,BC=3.求证:△BCD∽△BAC.
17.如图,在△ABC中,AB=AC,点D、E分别在BC、AB上,且∠BDE=∠CAD.
(1)求证:△BDE∽△CAD;
(2)求证:△ADE∽△ABD.
18.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB?AD;
(2)求证:△AFD∽△CFE.
参考答案
1.C
2.B
3.A
4.B
5.C
6.C
7.A
8.A
9.B
10.D
11.1或4
12.8.4或2或12
13.∠D=∠B(答案不唯一).
14.1或4或2.5
15.2或3
16.解:∵BD=2,AB=,BC=3.
∴=,==,
∴=,
而∠CBD=∠ABC,
∴△BCD∽△BAC.
17.(1)证明:∵AB=AC,
∴∠B=∠C,
又∵∠BDE=∠CAD,
∴△BDE∽△CAD;
(2)证明:∵△BDE∽△CAD,
∴∠BED=∠CDA,
∴180°﹣∠BED=180°﹣∠CDA
即∠AED=∠ADB.
又∵∠BAD=∠DAE,
∴△ADE∽△ABD.
18.(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB?AD;
(2)证明:∵E为AB的中点,
∴CE=BE=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD,
∴△AFD∽△CFE.
一.选择题
1.如图,已知在△ABC中,P为AB上一点,连接CP,以下条件中不能判定△ACP∽△ABC的是( )
A.∠ACP=∠B B.∠APC=∠ACB C. D.
2.下列正方形方格中四个三角形中,与甲图中的三角形相似的是( )
A. B.
C. D.
3.下列说法正确的是( )
A.所有等边三角形都相似
B.有一个角相等的两个等腰三角形相似
C.所有直角三角形都相似
D.所有矩形都相似
4.如图,点M在BC上,点N在AM上,CM=CN,,下列结论正确的是( )
A.△ABM∽△ACB B.△ANC∽△AMB C.△ANC∽△ACM D.△CMN∽△BCA
5.如图,△ABC中,点D在AB边上,点E在AC边上,且∠1=∠2=∠3,则与△ADE相似的三角形的个数为( )
A.4个 B.3个 C.2个 D.1个
6.如图,BE、CD相交于点A,连接BC,DE,下列条件中不能判断△ABC∽△ADE的是( )
A.∠B=∠D B.∠C=∠E C.= D.=
7.如图,△ABC中,∠A=60°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的三角形与△ABC不相似的是( )
A. B.
C. D.
8.如图,点A、B、C、D四点共线,△PBC是等边三角形,当△PAB∽△DPC时,∠APD的度数为( )
A.120° B.100° C.110° D.125°
9.在△ABC中,D、E分别在AB、AC上,给出下列条件:其中能判断△ADE∽△ABC的有( )
①;
②∠AED=∠B;
③;
④DE∥BC,
A.1个 B.2个 C.3个 D.4个
10.如图,在矩形ABCD中,点E,F分别在BC,CD边上,EF⊥AE,BH⊥AC于点H,EF与AC交于点M,BH与AE交于点N.则下列结论错误的是( )
A.△EFC∽△AEB B.△ECM∽△ABN C.△CFM∽△BEN D.△ANH∽△EFC
二.填空题
11.在△ABC中,AB=10,AC=5,点M在边AB上,且AM=2,点N在AC边上.当AN= 时,△AMN与原三角形相似.
12.如图,AB⊥BD,CD⊥BD,AB=6,CD=4,BD=14.点P在BD上移动,当以P,C,D为顶点的三角形与△ABP相似时,则PB的长为 .
13.如图,∠DAB=∠EAC,请补充一个条件: ,使△ADE∽△ABC(只写一个答案即可).
14.如图,矩形ABCD,AD=2,AB=5,P为CD边上的动点,当DP= 时,△ADP与△BCP相似.
15.如图,四边形ABCD中,∠A=∠B=90°,AB=5cm,AD=3cm,BC=2cm,P是AB上一点,若以P、A、D为顶点的三角形与△PBC相似,则PA= cm.
三.解答题
16.如图,D是△ABC的边AB上的一点,BD=2,AB=,BC=3.求证:△BCD∽△BAC.
17.如图,在△ABC中,AB=AC,点D、E分别在BC、AB上,且∠BDE=∠CAD.
(1)求证:△BDE∽△CAD;
(2)求证:△ADE∽△ABD.
18.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB?AD;
(2)求证:△AFD∽△CFE.
参考答案
1.C
2.B
3.A
4.B
5.C
6.C
7.A
8.A
9.B
10.D
11.1或4
12.8.4或2或12
13.∠D=∠B(答案不唯一).
14.1或4或2.5
15.2或3
16.解:∵BD=2,AB=,BC=3.
∴=,==,
∴=,
而∠CBD=∠ABC,
∴△BCD∽△BAC.
17.(1)证明:∵AB=AC,
∴∠B=∠C,
又∵∠BDE=∠CAD,
∴△BDE∽△CAD;
(2)证明:∵△BDE∽△CAD,
∴∠BED=∠CDA,
∴180°﹣∠BED=180°﹣∠CDA
即∠AED=∠ADB.
又∵∠BAD=∠DAE,
∴△ADE∽△ABD.
18.(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB?AD;
(2)证明:∵E为AB的中点,
∴CE=BE=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD,
∴△AFD∽△CFE.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
