人教版八年级上册数学 14.3因式分解 十字相乘与分组分解法分解因式 课件(15张)
文档属性
| 名称 | 人教版八年级上册数学 14.3因式分解 十字相乘与分组分解法分解因式 课件(15张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 598.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 00:00:00 | ||
图片预览



文档简介
用十字相乘和分组分解法分解因式
复习总结
1.因式分解:
把一个多项式转化为几个整式的积的形式.
2.我们已经学过哪些因式分解的方法?
①提公因式法
②平方差公式
a2-b2=(a+b)(a-b)
③完全平方公式
a2±2ab+b2=(a±b)2
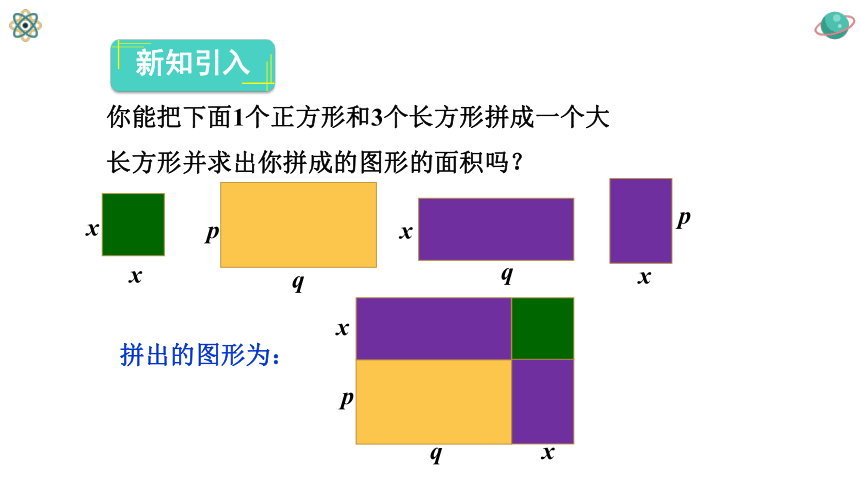
你能把下面1个正方形和3个长方形拼成一个大长方形并求出你拼成的图形的面积吗?
拼出的图形为:
新知引入
x
x
p
q
q
x
x
p
x
p
q
x
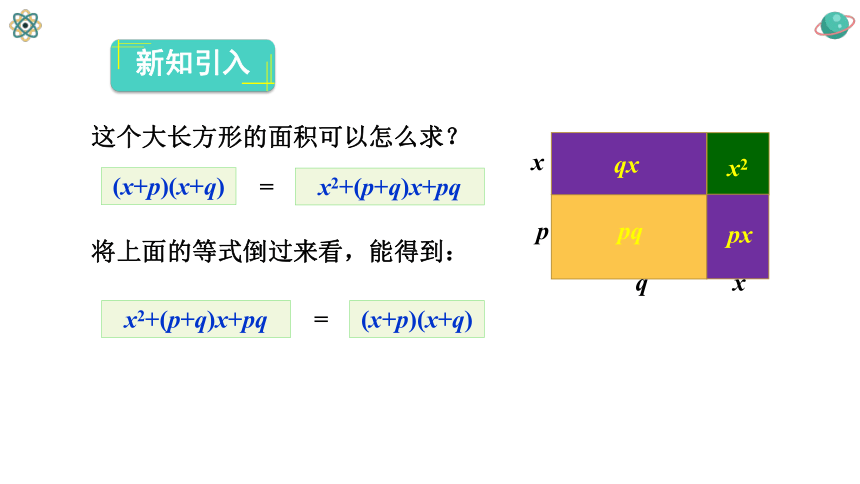
这个大长方形的面积可以怎么求?
(x+p)(x+q)
x2+(p+q)x+pq
=
将上面的等式倒过来看,能得到:
新知引入
=
x
p
q
x
x2+(p+q)x+pq
(x+p)(x+q)
px
pq
qx
x2
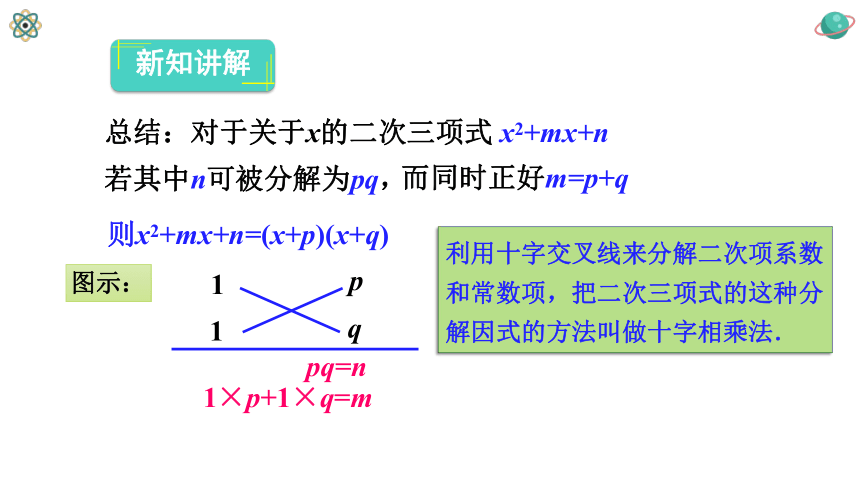
新知讲解
1
1
p
q
1×p+1×q=m
pq=n
总结:对于关于x的二次三项式 x2+mx+n
若其中n可被分解为pq,
而同时正好m=p+q
则x2+mx+n=(x+p)(x+q)
图示:
利用十字交叉线来分解二次项系数和常数项,把二次三项式的这种分解因式的方法叫做十字相乘法.
新知讲解
等式的特点:
x2+mx+n=(x+p)(x+q)
(1)等式左边是一个关于x的二次项系数为1的二次三项式;
(2)等式左边的常数项可以分解成两个因数的乘积,且这两个数的和等于一次项系数;
(3)等式右边为两个关于x的一次因式的乘积.
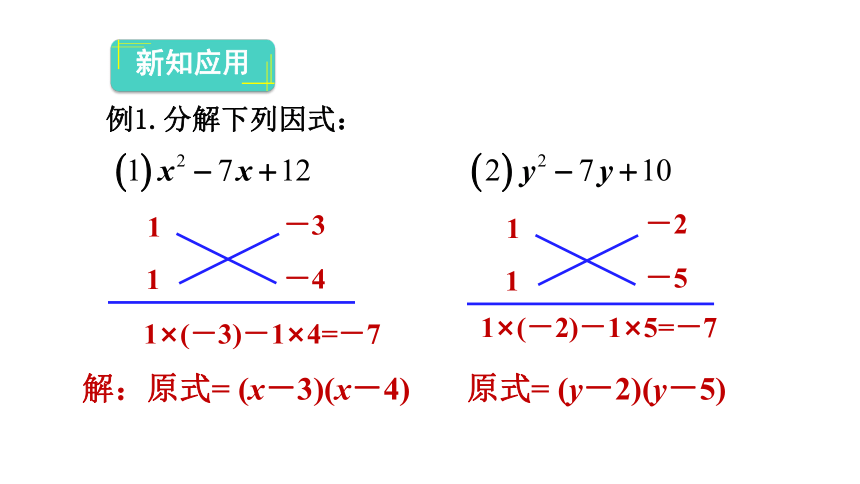
例1.分解下列因式:
解:原式= (x-3)(x-4)
1
1
-3
-4
1×(-3)-1×4=-7
新知应用
原式= (y-2)(y-5)
1
1
-2
-5
1×(-2)-1×5=-7
总结:十字相乘法的运用成功依赖于对原式结构的把握,有时需要多次尝试验证.
原式= (x+3)(x-4)
1
1
3
-4
1×3-1×4=-1
新知应用
1
1
5
-3
1×5-1×3=2
原式= (x+5)(x-3)
例2 分解下列因式:
①x2+5x-6;
新知应用
②10-3x-x2;
③(a+b)2-4(a+b)+3;
④ x2-4xy-12y2.
解:①原式= (x+6)(x-1);
②原式=-(x2+3x-10)=(x+5)(x-2);
③原式=(a+b-1)(a+b-3);
④原式=(x-6y)(x+2y).
二次项系数调整为1
整体思想的应用
把含y的二次项看为常数项
问题:下列因式能分解吗
没有公因式,不能套用公式,如何分解呢?
新知讲解
合理分组后还是可以分解因式的!
请分解下列因式
跟踪练习
(2)分组分解法可能第一次的分组不会成功,甚至前几次都不会成功,这时一方面展现我们的数感,更重要的展现我们的意志品质.
(1)若待分解的多项式既没有公因式,又项数多于3项,可以考虑运用加法结合律,将各项适当分组,先局部分解,再观察各组分解的结果中是否存在公因式,可否进一步分解因式.
归纳总结
新知应用
例1 请分解下列因式:
新知应用
例2 把下列多项式分解因式:
x2+(p+q)x+pq=(x+p)(x+q).
课堂总结
当多项式的项数多于3项,将各项适当分组,先局部分解,再观察各组分解的结果中是否存有公因式或能用公式,再进一步分解因式.
(1)分解思路为“看两端,凑中间”;
(2)二次项系数一般都化为正数,如果是负数,则提出负号,分解括号里面的二次三项式,最后结果不要忘记把提出的负号添上.
十字相乘法
分解因式
分组分解法
分解因式:
复习总结
1.因式分解:
把一个多项式转化为几个整式的积的形式.
2.我们已经学过哪些因式分解的方法?
①提公因式法
②平方差公式
a2-b2=(a+b)(a-b)
③完全平方公式
a2±2ab+b2=(a±b)2
你能把下面1个正方形和3个长方形拼成一个大长方形并求出你拼成的图形的面积吗?
拼出的图形为:
新知引入
x
x
p
q
q
x
x
p
x
p
q
x
这个大长方形的面积可以怎么求?
(x+p)(x+q)
x2+(p+q)x+pq
=
将上面的等式倒过来看,能得到:
新知引入
=
x
p
q
x
x2+(p+q)x+pq
(x+p)(x+q)
px
pq
qx
x2
新知讲解
1
1
p
q
1×p+1×q=m
pq=n
总结:对于关于x的二次三项式 x2+mx+n
若其中n可被分解为pq,
而同时正好m=p+q
则x2+mx+n=(x+p)(x+q)
图示:
利用十字交叉线来分解二次项系数和常数项,把二次三项式的这种分解因式的方法叫做十字相乘法.
新知讲解
等式的特点:
x2+mx+n=(x+p)(x+q)
(1)等式左边是一个关于x的二次项系数为1的二次三项式;
(2)等式左边的常数项可以分解成两个因数的乘积,且这两个数的和等于一次项系数;
(3)等式右边为两个关于x的一次因式的乘积.
例1.分解下列因式:
解:原式= (x-3)(x-4)
1
1
-3
-4
1×(-3)-1×4=-7
新知应用
原式= (y-2)(y-5)
1
1
-2
-5
1×(-2)-1×5=-7
总结:十字相乘法的运用成功依赖于对原式结构的把握,有时需要多次尝试验证.
原式= (x+3)(x-4)
1
1
3
-4
1×3-1×4=-1
新知应用
1
1
5
-3
1×5-1×3=2
原式= (x+5)(x-3)
例2 分解下列因式:
①x2+5x-6;
新知应用
②10-3x-x2;
③(a+b)2-4(a+b)+3;
④ x2-4xy-12y2.
解:①原式= (x+6)(x-1);
②原式=-(x2+3x-10)=(x+5)(x-2);
③原式=(a+b-1)(a+b-3);
④原式=(x-6y)(x+2y).
二次项系数调整为1
整体思想的应用
把含y的二次项看为常数项
问题:下列因式能分解吗
没有公因式,不能套用公式,如何分解呢?
新知讲解
合理分组后还是可以分解因式的!
请分解下列因式
跟踪练习
(2)分组分解法可能第一次的分组不会成功,甚至前几次都不会成功,这时一方面展现我们的数感,更重要的展现我们的意志品质.
(1)若待分解的多项式既没有公因式,又项数多于3项,可以考虑运用加法结合律,将各项适当分组,先局部分解,再观察各组分解的结果中是否存在公因式,可否进一步分解因式.
归纳总结
新知应用
例1 请分解下列因式:
新知应用
例2 把下列多项式分解因式:
x2+(p+q)x+pq=(x+p)(x+q).
课堂总结
当多项式的项数多于3项,将各项适当分组,先局部分解,再观察各组分解的结果中是否存有公因式或能用公式,再进一步分解因式.
(1)分解思路为“看两端,凑中间”;
(2)二次项系数一般都化为正数,如果是负数,则提出负号,分解括号里面的二次三项式,最后结果不要忘记把提出的负号添上.
十字相乘法
分解因式
分组分解法
分解因式:
