初中数学湘教版八年级上册2.5全等三角形练习题(Word版含解析)
文档属性
| 名称 | 初中数学湘教版八年级上册2.5全等三角形练习题(Word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 122.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 07:49:32 | ||
图片预览



文档简介
初中数学湘教版八年级上册第二章2.5全等三角形练习题
一、选择题
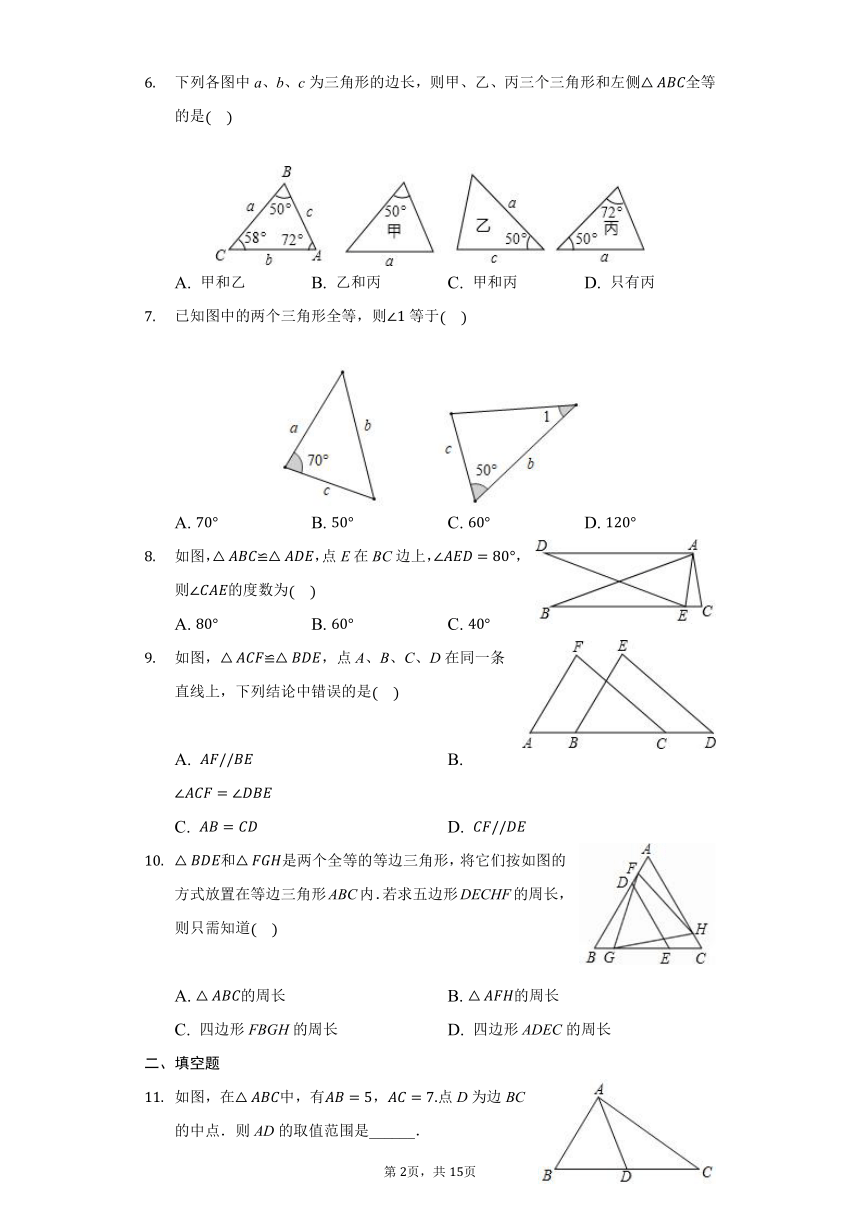
如图,点B、E、A、D在同一条直线上,≌,,,则AD的长是
A.
4
B.
5
C.
6
D.
7
如图,在中,,添加下列条件后,还不能使≌的是
A.
B.
C.
D.
如图,已知≌,若,则的度数是
A.
B.
C.
D.
如图,某同学一不小心将三角形玻璃打碎,现要带到玻璃店配一块完全相同的玻璃,这样做的依据是
A.
ASA
B.
SAS
C.
AAS
D.
SSS
如图,≌,若,,则AB长为
A.
6
B.
5
C.
4
D.
3
下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧全等的是
A.
甲和乙
B.
乙和丙
C.
甲和丙
D.
只有丙
已知图中的两个三角形全等,则等于
A.
B.
C.
D.
如图,≌,点E在BC边上,,则的度数为
A.
B.
C.
D.
如图,≌,点A、B、C、D在同一条直线上,下列结论中错误的是
A.
B.
C.
D.
和是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长,则只需知道
A.
的周长
B.
的周长
C.
四边形FBGH的周长
D.
四边形ADEC的周长
二、填空题
如图,在中,有,点D为边BC的中点.则AD的取值范围是______.
如图,,,,,点P和点Q同时从点A出发,分别在线段AC和射线AX上运动,且,当______时,以点A,P,Q为顶点的三角形与全等.
如图,中,,,,在AB上截取BE,使,过点B作AB的垂线,交CD于点F,连接DE,交BC于点H,交BF于点G,,,则______.
如图,D在BC边上,≌,,则的度数为______.
三、解答题
如图,,,于E,于,,求BE的长度.
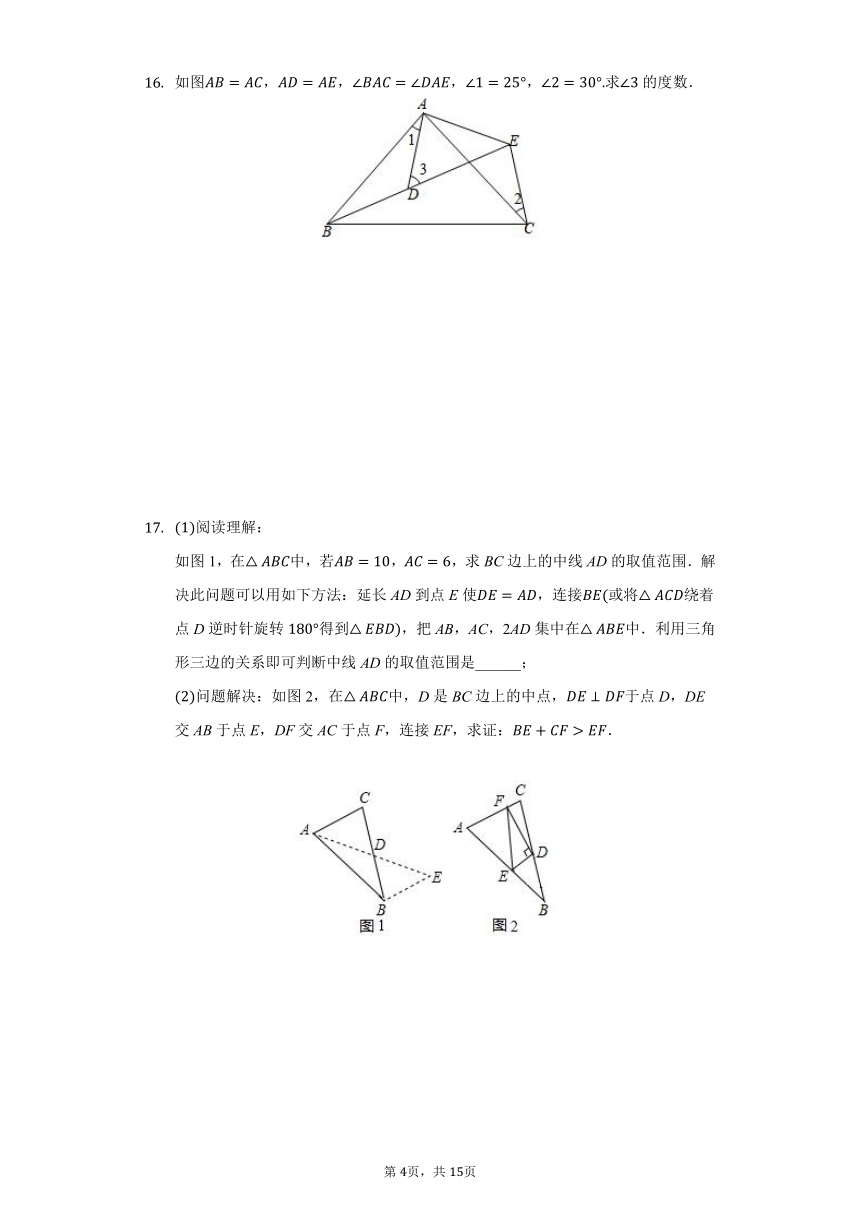
如图,,,,求的度数.
阅读理解:
如图1,在中,若,,求BC边上的中线AD的取值范围.解决此问题可以用如下方法:延长AD到点E使,连接或将绕着点D逆时针旋转得到,把AB,AC,2AD集中在中.利用三角形三边的关系即可判断中线AD的取值范围是______;
问题解决:如图2,在中,D是BC边上的中点,于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:.
答案和解析
1.【答案】B
【解析】解:≌,
,
,
,
,,
,
.
故选:B.
根据全等三角形的性质可得,再根据等式的性质可得,进而可得答案.
此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应边相等.
2.【答案】D
【解析】解:,
,
A、在和中
≌,故本选项不符合题意;
B、在和中
≌,故本选项不符合题意;
C、在和中
≌,故本选项不符合题意;
D、在和中,根据和不能推出≌,故本选项符合题意;
故选:D.
根据全等三角形的判定定理推出即可.
本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理的内容是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.
3.【答案】B
【解析】解:≌,
,
.
故选:B.
直接利用全等三角形的性质得出,进而得出答案.
此题主要考查了全等三角形的性质,得出对应角相等是解题关键.
4.【答案】A
【解析】解:第一块,仅保留了原三角形的一个角和部分边,不符合全等三角形的判定方法;
第二块,仅保留了原三角形的一部分边,所以此块玻璃也不行;
第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定,所以应该拿这块去.
故选:A.
根据全等三角形的判定方法,在打碎的三块中可以采用排除法进行分析从而确定最后的答案.
本题主要考查了全等三角形的应用,要求对常用的几种方法熟练掌握.在解答时要求对全等三角形的判定方法的运用灵活.
5.【答案】D
【解析】解:≌,
,
,
即,
,,
.
故选:D.
根据全等三角形的对应边相等可得,然后求出,代入数据计算即可得解.
本题考查了全等三角形对应边相等的性质,熟记性质并求出是解题的关键.
6.【答案】B
【解析】解:乙和全等;理由如下:
在和图乙的三角形中,满足三角形全等的判定方法:SAS,
所以乙和全等;
在和图丙的三角形中,满足三角形全等的判定方法:AAS,
所以丙和全等;
不能判定甲与全等;
故选:B.
根据三角形全等的判定方法得出乙和丙与全等,甲与不全等.
本题考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
7.【答案】C
【解析】解:≌,
,
,
故选:C.
根据全等三角形的性质求出,根据三角形内角和定理计算,得到答案.
本题考查的是全等三角形的性质、三角形内角和定理,掌握全等三角形的对应角相等是解题的关键.
8.【答案】D
【解析】解:≌,,
,,
,
,
故选:D.
根据全等三角形的性质得出,,根据等腰三角形的性质得出,根据三角形内角和定理求出即可.
本题考查了全等三角形的性质,等腰三角形的性质和三角形的内角和定理,能熟记全等三角形的性质定理的内容是解此题的关键,注意:全等三角形的对应边相等,对应角相等.
9.【答案】B
【解析】解:≌,
,
,A正确,不符合题意;
,B错误,符合题意;
,
,C正确,不符合题意;
,
,D正确,不符合题意;
故选:B.
根据全等三角形的性质、平行线的判定定理判断即可.
本题考查的是全等三角形的性质,掌握全等三角形的对应边相等、对应角相等是解题的关键.
10.【答案】A
【解析】解:为等边三角形,
,,
,
为等边三角形,
,,
,
,
≌,
.
和是两个全等的等边三角形,
,
五边形DECHF的周长,
,
.
只需知道的周长即可.
故选:A.
证明≌,得出由题意可知,则得出五边形DECHF的周长,则可得出答案.
本题考查了全等三角形的判定与性质,等边三角形的性质,熟练掌握全等三角形的判定方法是解题的关键.
11.【答案】
【解析】解:如图,延长AD到E,使,连接BE,
点D为边BC的中点,
,且,,
≌
,
在中,,
,
,
故答案为:.
如图,延长AD到E,使,由“SAS”可证≌,可得,由三角形的三边关系可求解.
本题考查了全等三角形的判定和性质,三角形的三边关系,添加恰当辅助线构造全等三角形是本题的关键.
12.【答案】10或20
【解析】解:,
,
,
分两种情况:
当时,
在和中,
,
≌;
当时,
在和中,
,
≌;
综上所述:当点P运动到或20时,与全等;
故答案为:10或20.
分两种情况:当时;当时;由HL证明≌;即可得出结果.
本题考查了直角三角形全等的判定方法;熟练掌握直角三角形全等的判定方法,本题需要分类讨论,难度适中.
13.【答案】
【解析】解:,,
,
,,
,
,
,
,
≌,
,,
,,
≌,
,
,
故答案为:.
根据,又,可得:,再根据AAS即可证明≌,根据全等三角形的性质,,然后再证明≌得到得到,在直角中,利用勾股定理即可求解.
本题主要考查了三角形全等的判定和性质,以及勾股定理,把梯形的问题转化为三角形的问题是解题的关键.
14.【答案】
【解析】解:≌,
,,
,
,
,
,
,
,
故答案为:.
根据全等三角形的性质得出,,求出,根据等腰三角形的性质得出,即可求出答案.
本题考查了全等三角形的性质,等腰三角形的性质和三角形内角和定理等知识点,能根据全等三角形的性质得出和求出是解此题的关键.
15.【答案】解:,,
,
,,
,
在和中,
,
≌,
,,
,
.
【解析】根据AAS证出≌,根据全等三角形的性质得出,即可.
本题考查了全等三角形的性质和判定的应用,解此题的关键是推出≌.
16.【答案】解:,
,
.
在和AEC中,
,
≌,
.
.
.
答:的度数为.
【解析】先由,就可以得出,就可以得出≌AEC,就可以得出,就可以由三角形的外角与内角的关系求出结论.
本题考查全等三角形的判定及性质的运用,三角形的外角与内角的关系的运用,解答时证明三角形的全等是关键.
17.【答案】
如图2所示:延长FD至点M,使,连接BM、EM,
同得:≌,
,
,,
,
在中,由三角形的三边关系得:,
.
【解析】
解:如图1所示:延长AD至E,使,连接BE,
是BC边上的中线,
,
在和中,
,
≌,
,
在中,由三角形的三边关系得:,
,即,
;
故答案为:;
见答案
【分析】
延长AD至E,使,由SAS证明≌,得出,在中,由三角形的三边关系求出AE的取值范围,即可得出AD的取值范围;
延长FD至点M,使,连接BM、EM,同得≌,得出,由线段垂直平分线的性质得出,在中,由三角形的三边关系得出即可得出结论.
本题是三角形的综合问题,考查了三角形的三边关系、全等三角形的判定与性质、角的关系等知识;本题综合性强,有一定难度,通过作辅助线证明三角形全等是解决问题的关键.
第2页,共2页
第1页,共1页
一、选择题
如图,点B、E、A、D在同一条直线上,≌,,,则AD的长是
A.
4
B.
5
C.
6
D.
7
如图,在中,,添加下列条件后,还不能使≌的是
A.
B.
C.
D.
如图,已知≌,若,则的度数是
A.
B.
C.
D.
如图,某同学一不小心将三角形玻璃打碎,现要带到玻璃店配一块完全相同的玻璃,这样做的依据是
A.
ASA
B.
SAS
C.
AAS
D.
SSS
如图,≌,若,,则AB长为
A.
6
B.
5
C.
4
D.
3
下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧全等的是
A.
甲和乙
B.
乙和丙
C.
甲和丙
D.
只有丙
已知图中的两个三角形全等,则等于
A.
B.
C.
D.
如图,≌,点E在BC边上,,则的度数为
A.
B.
C.
D.
如图,≌,点A、B、C、D在同一条直线上,下列结论中错误的是
A.
B.
C.
D.
和是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长,则只需知道
A.
的周长
B.
的周长
C.
四边形FBGH的周长
D.
四边形ADEC的周长
二、填空题
如图,在中,有,点D为边BC的中点.则AD的取值范围是______.
如图,,,,,点P和点Q同时从点A出发,分别在线段AC和射线AX上运动,且,当______时,以点A,P,Q为顶点的三角形与全等.
如图,中,,,,在AB上截取BE,使,过点B作AB的垂线,交CD于点F,连接DE,交BC于点H,交BF于点G,,,则______.
如图,D在BC边上,≌,,则的度数为______.
三、解答题
如图,,,于E,于,,求BE的长度.
如图,,,,求的度数.
阅读理解:
如图1,在中,若,,求BC边上的中线AD的取值范围.解决此问题可以用如下方法:延长AD到点E使,连接或将绕着点D逆时针旋转得到,把AB,AC,2AD集中在中.利用三角形三边的关系即可判断中线AD的取值范围是______;
问题解决:如图2,在中,D是BC边上的中点,于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:.
答案和解析
1.【答案】B
【解析】解:≌,
,
,
,
,,
,
.
故选:B.
根据全等三角形的性质可得,再根据等式的性质可得,进而可得答案.
此题主要考查了全等三角形的性质,关键是掌握全等三角形的对应边相等.
2.【答案】D
【解析】解:,
,
A、在和中
≌,故本选项不符合题意;
B、在和中
≌,故本选项不符合题意;
C、在和中
≌,故本选项不符合题意;
D、在和中,根据和不能推出≌,故本选项符合题意;
故选:D.
根据全等三角形的判定定理推出即可.
本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理的内容是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.
3.【答案】B
【解析】解:≌,
,
.
故选:B.
直接利用全等三角形的性质得出,进而得出答案.
此题主要考查了全等三角形的性质,得出对应角相等是解题关键.
4.【答案】A
【解析】解:第一块,仅保留了原三角形的一个角和部分边,不符合全等三角形的判定方法;
第二块,仅保留了原三角形的一部分边,所以此块玻璃也不行;
第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定,所以应该拿这块去.
故选:A.
根据全等三角形的判定方法,在打碎的三块中可以采用排除法进行分析从而确定最后的答案.
本题主要考查了全等三角形的应用,要求对常用的几种方法熟练掌握.在解答时要求对全等三角形的判定方法的运用灵活.
5.【答案】D
【解析】解:≌,
,
,
即,
,,
.
故选:D.
根据全等三角形的对应边相等可得,然后求出,代入数据计算即可得解.
本题考查了全等三角形对应边相等的性质,熟记性质并求出是解题的关键.
6.【答案】B
【解析】解:乙和全等;理由如下:
在和图乙的三角形中,满足三角形全等的判定方法:SAS,
所以乙和全等;
在和图丙的三角形中,满足三角形全等的判定方法:AAS,
所以丙和全等;
不能判定甲与全等;
故选:B.
根据三角形全等的判定方法得出乙和丙与全等,甲与不全等.
本题考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
7.【答案】C
【解析】解:≌,
,
,
故选:C.
根据全等三角形的性质求出,根据三角形内角和定理计算,得到答案.
本题考查的是全等三角形的性质、三角形内角和定理,掌握全等三角形的对应角相等是解题的关键.
8.【答案】D
【解析】解:≌,,
,,
,
,
故选:D.
根据全等三角形的性质得出,,根据等腰三角形的性质得出,根据三角形内角和定理求出即可.
本题考查了全等三角形的性质,等腰三角形的性质和三角形的内角和定理,能熟记全等三角形的性质定理的内容是解此题的关键,注意:全等三角形的对应边相等,对应角相等.
9.【答案】B
【解析】解:≌,
,
,A正确,不符合题意;
,B错误,符合题意;
,
,C正确,不符合题意;
,
,D正确,不符合题意;
故选:B.
根据全等三角形的性质、平行线的判定定理判断即可.
本题考查的是全等三角形的性质,掌握全等三角形的对应边相等、对应角相等是解题的关键.
10.【答案】A
【解析】解:为等边三角形,
,,
,
为等边三角形,
,,
,
,
≌,
.
和是两个全等的等边三角形,
,
五边形DECHF的周长,
,
.
只需知道的周长即可.
故选:A.
证明≌,得出由题意可知,则得出五边形DECHF的周长,则可得出答案.
本题考查了全等三角形的判定与性质,等边三角形的性质,熟练掌握全等三角形的判定方法是解题的关键.
11.【答案】
【解析】解:如图,延长AD到E,使,连接BE,
点D为边BC的中点,
,且,,
≌
,
在中,,
,
,
故答案为:.
如图,延长AD到E,使,由“SAS”可证≌,可得,由三角形的三边关系可求解.
本题考查了全等三角形的判定和性质,三角形的三边关系,添加恰当辅助线构造全等三角形是本题的关键.
12.【答案】10或20
【解析】解:,
,
,
分两种情况:
当时,
在和中,
,
≌;
当时,
在和中,
,
≌;
综上所述:当点P运动到或20时,与全等;
故答案为:10或20.
分两种情况:当时;当时;由HL证明≌;即可得出结果.
本题考查了直角三角形全等的判定方法;熟练掌握直角三角形全等的判定方法,本题需要分类讨论,难度适中.
13.【答案】
【解析】解:,,
,
,,
,
,
,
,
≌,
,,
,,
≌,
,
,
故答案为:.
根据,又,可得:,再根据AAS即可证明≌,根据全等三角形的性质,,然后再证明≌得到得到,在直角中,利用勾股定理即可求解.
本题主要考查了三角形全等的判定和性质,以及勾股定理,把梯形的问题转化为三角形的问题是解题的关键.
14.【答案】
【解析】解:≌,
,,
,
,
,
,
,
,
故答案为:.
根据全等三角形的性质得出,,求出,根据等腰三角形的性质得出,即可求出答案.
本题考查了全等三角形的性质,等腰三角形的性质和三角形内角和定理等知识点,能根据全等三角形的性质得出和求出是解此题的关键.
15.【答案】解:,,
,
,,
,
在和中,
,
≌,
,,
,
.
【解析】根据AAS证出≌,根据全等三角形的性质得出,即可.
本题考查了全等三角形的性质和判定的应用,解此题的关键是推出≌.
16.【答案】解:,
,
.
在和AEC中,
,
≌,
.
.
.
答:的度数为.
【解析】先由,就可以得出,就可以得出≌AEC,就可以得出,就可以由三角形的外角与内角的关系求出结论.
本题考查全等三角形的判定及性质的运用,三角形的外角与内角的关系的运用,解答时证明三角形的全等是关键.
17.【答案】
如图2所示:延长FD至点M,使,连接BM、EM,
同得:≌,
,
,,
,
在中,由三角形的三边关系得:,
.
【解析】
解:如图1所示:延长AD至E,使,连接BE,
是BC边上的中线,
,
在和中,
,
≌,
,
在中,由三角形的三边关系得:,
,即,
;
故答案为:;
见答案
【分析】
延长AD至E,使,由SAS证明≌,得出,在中,由三角形的三边关系求出AE的取值范围,即可得出AD的取值范围;
延长FD至点M,使,连接BM、EM,同得≌,得出,由线段垂直平分线的性质得出,在中,由三角形的三边关系得出即可得出结论.
本题是三角形的综合问题,考查了三角形的三边关系、全等三角形的判定与性质、角的关系等知识;本题综合性强,有一定难度,通过作辅助线证明三角形全等是解决问题的关键.
第2页,共2页
第1页,共1页
同课章节目录
