《5.2.1三角函数的概念(第一课时)课件(20张PPT)
文档属性
| 名称 | 《5.2.1三角函数的概念(第一课时)课件(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 227.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 00:00:00 | ||
图片预览








文档简介
5. 2. 1 三角函数的概念
第一课时
明确研究背景—对应关系的特点分析—下定义—研究性质.
创设情境
问题1 如图,单位圆⊙O上的点P以A为起点做逆时针方向旋转,建立一个函数模型,刻画点P的位置变化情况.根据已有的研究函数的经验,你认为我们可以按怎样的路径研究上述问题?
x
y
O
α
A(1, 0)
P(x, y)
一般地,任意给定一个角α,它的终边OP与单位圆交点P的坐标能唯一确定吗?
都是唯一确定的.
新知探究
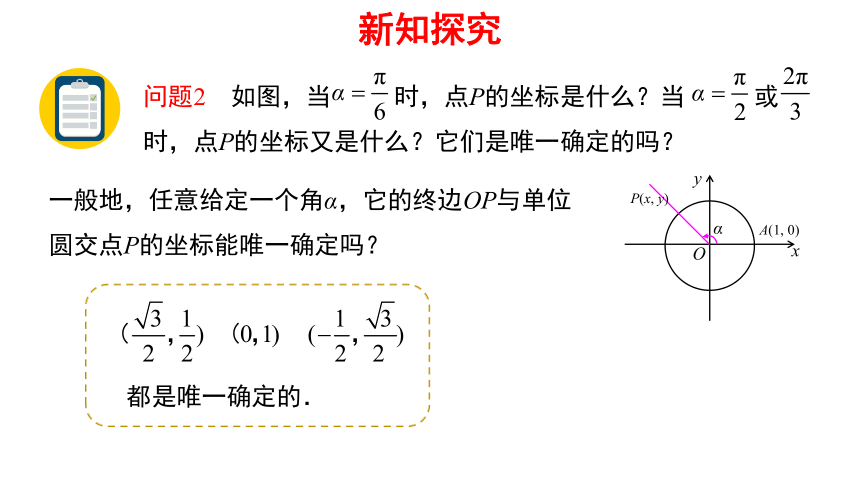
问题2 如图,当 时,点P的坐标是什么?当 或 时,点P的坐标又是什么?它们是唯一确定的吗?
(1)正弦函数、余弦函数和正切函数的对应关系各是什么?
(2)符号sin?,cos?和tan?分别表示什么?在你以往的学习中有类似的引入特定符号表示一种量的经历吗?
(3)为什么说当 时,tan?的值是唯一确定的?
(4)为什么说正弦函数、余弦函数的定义域是R?而正切函数的定义域是 ?
新知探究
问题3 请同学们先阅读教科书第178~179页,再回答如下问题:
(1)正弦函数、余弦函数和正切函数的对应关系各是什么?
新知探究
问题3 请同学们先阅读教科书第178~179页,再回答如下问题:
(1)正弦函数的对应关系:?→点P的纵坐标y;
余弦函数的对应关系:?→点P的横坐标x;
正弦函数的对应关系:?→
(2)符号sin?,cos?和tan?分别表示什么?在你以往的学习中有类似的引入特定符号表示一种量的经历吗?
新知探究
问题3 请同学们先阅读教科书第178~179页,再回答如下问题:
(2)分别表示y,x, ;引入符号logab表示ax=b中的x.
新知探究
问题3 请同学们先阅读教科书第178~179页,再回答如下问题:
(3)为什么说当 时,tan?的值是唯一确定的?
(3)当 时,如果α确定,那么α的终边确定,
终边与单位圆的交点P确定,
P 点的横、纵坐标x、y就会唯一确定,
新知探究
问题3 请同学们先阅读教科书第178~179页,再回答如下问题:
(3)为什么说当 时,tan?的值是唯一确定的?
因此 的值也是唯一确定的,
所以tan α的值也是唯一确定的.
新知探究
问题3 请同学们先阅读教科书第178~179页,再回答如下问题:
(4)为什么说正弦函数、余弦函数的定义域是R?而正切函数的定义域是 ?
(4)当 时,α的终边在y轴上,
这时点P的横坐标x等于0,所以 无意义.
除此之外,对于任意角α,P点的横、纵坐标的值x,y都是存在且唯一确定的.
再将它放入直角坐标系中,使点A与原点重合,
AC在x轴的正半轴上,可得出y1=z1的结论.
对于余弦、正切也有相同的结论.
新知探究
问题5 在初中我们学了锐角三角函数,知道它们都是以锐角为自变量,以比值为函数值的函数.设 ,把按锐角三角函数定义求得的锐角x的正弦记为y1,并把按本节三角函数定义求得的x的正弦记为z1.y1与z1相等吗?对于余弦、正切也有相同的结论吗?
解答:作出Rt△ABC,其中∠A=x,∠C=90°,
解:如图,在直角坐标系中,作 ,
易知∠AOB的终边与单位圆的交点坐标为 ,
所以
新知探究
例1 利用三角函数的定义求 的正弦、余弦和正切值.
课堂练习:
(1)利用三角函数定义,求 的三个三角函数值.
(2)说出几个使cos α=1的α的值.
解:(1)sin π=0,cos π=-1,tan π=0;
不存在.
(2)α=0,2π,-2π等.
新知探究
M0
M
证明:设角α的终边与单位圆交于点P0(x0,y0).
分别过点P,P0作x轴的垂线PM,P0M0,垂足分别为M,M0,
P0
x
y
O
P
则|P0M0|=|y0|,|PM|=|y|,|OM0|=|x0|,|OM|=|x|,
新知探究
例2 如图,设α是一个任意角,它的终边上任意一点P(不与原点O重合)的坐标为(x,y),点P与原点的距离为r.
求证:
△OMP∽△OM0P0.
因为y0与y同号,
所以 ,即 .
同理可得
新知探究
于是 ,即 .
M0
M
P0
x
y
O
P
例2 如图,设α是一个任意角,它的终边上任意一点P(不与原点O重合)的坐标为(x,y),点P与原点的距离为r.
求证:
追问:例2实际上给出了任意角三角函数的另外一种定义,而且这种定义与已有的定义是等价的.你能用严格的数学语言叙述一下这种定义吗?
解:设α是一个任意角,
点P与原点的距离为r,
它的终边上任意一点P(不与原点O重合)的坐标为(x,y),
则 分别叫做角α的正弦、余弦、正切.
新知探究
课堂练习:
(3)已知点P在半径为2的圆上按顺时针方向做匀速圆周运动,角速度为1 rad/s.求2 s时点P所在的位置.
解:以坐标原点为圆心O,
OP所在直线为x轴正方向建立平面直角坐标系.
2 s时点P所在位置记为Q.
因为点P是在半径为2的圆上按顺时针方向作匀速圆周运动,
角速度为1 rad/s,所以圆心角∠POQ=-2 rad.
新知探究
所以2 s时,点P在该坐标系中的位置为(2cos 2,-2sin 2).
作业布置
作业: 1.第175页练习;
2.第175页习题5.1A组1-9题.
目标检测
利用三角函数定义,求 的三个三角函数值.
1
答案:
目标检测
已知角θ的终边过点P(-12,5),求角θ的三角函数值.
2
答案:
再见
第一课时
明确研究背景—对应关系的特点分析—下定义—研究性质.
创设情境
问题1 如图,单位圆⊙O上的点P以A为起点做逆时针方向旋转,建立一个函数模型,刻画点P的位置变化情况.根据已有的研究函数的经验,你认为我们可以按怎样的路径研究上述问题?
x
y
O
α
A(1, 0)
P(x, y)
一般地,任意给定一个角α,它的终边OP与单位圆交点P的坐标能唯一确定吗?
都是唯一确定的.
新知探究
问题2 如图,当 时,点P的坐标是什么?当 或 时,点P的坐标又是什么?它们是唯一确定的吗?
(1)正弦函数、余弦函数和正切函数的对应关系各是什么?
(2)符号sin?,cos?和tan?分别表示什么?在你以往的学习中有类似的引入特定符号表示一种量的经历吗?
(3)为什么说当 时,tan?的值是唯一确定的?
(4)为什么说正弦函数、余弦函数的定义域是R?而正切函数的定义域是 ?
新知探究
问题3 请同学们先阅读教科书第178~179页,再回答如下问题:
(1)正弦函数、余弦函数和正切函数的对应关系各是什么?
新知探究
问题3 请同学们先阅读教科书第178~179页,再回答如下问题:
(1)正弦函数的对应关系:?→点P的纵坐标y;
余弦函数的对应关系:?→点P的横坐标x;
正弦函数的对应关系:?→
(2)符号sin?,cos?和tan?分别表示什么?在你以往的学习中有类似的引入特定符号表示一种量的经历吗?
新知探究
问题3 请同学们先阅读教科书第178~179页,再回答如下问题:
(2)分别表示y,x, ;引入符号logab表示ax=b中的x.
新知探究
问题3 请同学们先阅读教科书第178~179页,再回答如下问题:
(3)为什么说当 时,tan?的值是唯一确定的?
(3)当 时,如果α确定,那么α的终边确定,
终边与单位圆的交点P确定,
P 点的横、纵坐标x、y就会唯一确定,
新知探究
问题3 请同学们先阅读教科书第178~179页,再回答如下问题:
(3)为什么说当 时,tan?的值是唯一确定的?
因此 的值也是唯一确定的,
所以tan α的值也是唯一确定的.
新知探究
问题3 请同学们先阅读教科书第178~179页,再回答如下问题:
(4)为什么说正弦函数、余弦函数的定义域是R?而正切函数的定义域是 ?
(4)当 时,α的终边在y轴上,
这时点P的横坐标x等于0,所以 无意义.
除此之外,对于任意角α,P点的横、纵坐标的值x,y都是存在且唯一确定的.
再将它放入直角坐标系中,使点A与原点重合,
AC在x轴的正半轴上,可得出y1=z1的结论.
对于余弦、正切也有相同的结论.
新知探究
问题5 在初中我们学了锐角三角函数,知道它们都是以锐角为自变量,以比值为函数值的函数.设 ,把按锐角三角函数定义求得的锐角x的正弦记为y1,并把按本节三角函数定义求得的x的正弦记为z1.y1与z1相等吗?对于余弦、正切也有相同的结论吗?
解答:作出Rt△ABC,其中∠A=x,∠C=90°,
解:如图,在直角坐标系中,作 ,
易知∠AOB的终边与单位圆的交点坐标为 ,
所以
新知探究
例1 利用三角函数的定义求 的正弦、余弦和正切值.
课堂练习:
(1)利用三角函数定义,求 的三个三角函数值.
(2)说出几个使cos α=1的α的值.
解:(1)sin π=0,cos π=-1,tan π=0;
不存在.
(2)α=0,2π,-2π等.
新知探究
M0
M
证明:设角α的终边与单位圆交于点P0(x0,y0).
分别过点P,P0作x轴的垂线PM,P0M0,垂足分别为M,M0,
P0
x
y
O
P
则|P0M0|=|y0|,|PM|=|y|,|OM0|=|x0|,|OM|=|x|,
新知探究
例2 如图,设α是一个任意角,它的终边上任意一点P(不与原点O重合)的坐标为(x,y),点P与原点的距离为r.
求证:
△OMP∽△OM0P0.
因为y0与y同号,
所以 ,即 .
同理可得
新知探究
于是 ,即 .
M0
M
P0
x
y
O
P
例2 如图,设α是一个任意角,它的终边上任意一点P(不与原点O重合)的坐标为(x,y),点P与原点的距离为r.
求证:
追问:例2实际上给出了任意角三角函数的另外一种定义,而且这种定义与已有的定义是等价的.你能用严格的数学语言叙述一下这种定义吗?
解:设α是一个任意角,
点P与原点的距离为r,
它的终边上任意一点P(不与原点O重合)的坐标为(x,y),
则 分别叫做角α的正弦、余弦、正切.
新知探究
课堂练习:
(3)已知点P在半径为2的圆上按顺时针方向做匀速圆周运动,角速度为1 rad/s.求2 s时点P所在的位置.
解:以坐标原点为圆心O,
OP所在直线为x轴正方向建立平面直角坐标系.
2 s时点P所在位置记为Q.
因为点P是在半径为2的圆上按顺时针方向作匀速圆周运动,
角速度为1 rad/s,所以圆心角∠POQ=-2 rad.
新知探究
所以2 s时,点P在该坐标系中的位置为(2cos 2,-2sin 2).
作业布置
作业: 1.第175页练习;
2.第175页习题5.1A组1-9题.
目标检测
利用三角函数定义,求 的三个三角函数值.
1
答案:
目标检测
已知角θ的终边过点P(-12,5),求角θ的三角函数值.
2
答案:
再见
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
