整式的乘除复习
图片预览







文档简介
(共25张PPT)
整式的乘除
(复习课)
四川师范大学实验外国语学校
杜林峰
书 山 有 路 勤 为 径,学 海 无 崖 法 作 舟
少 小 不 学 习,老 来 徒 伤 悲
天才就是百分之一的灵感,百分之九十九的汗水!
成功=艰苦的劳动+正确的方法+少谈空话
欢 迎 光 临!欢 迎 指 导!
欢 迎 光 临!欢 迎 指 导!
欢 迎 光 临!欢 迎 指 导!
欢 迎 光 临!欢 迎 指 导!
重难点知识归纳
重点 整式的乘除法,乘法公式的应用
难点 整式乘法公式的应用
要突破上述难点,先要认真掌握好乘法公式的基本结构,再要针对性地加强练习,以达到熟练自如的目的。
知识表解
研究性学习
学习本章知识,先得有较好的转化意识,即善于化新为旧,如把单项式乘法转化为有理数乘法和同底数幂的乘法等,这样,新知识的学习就不难了。
同时要特别逆用一些法则、公式,这样会为解题提供方便、简洁的解法,也锻炼了思维能力。
解题方法技巧
1、归纳法 如本章的一些性质、法则、公式的导出,一般都是由特殊到一般归纳得到的。
2、转化法 如单项式乘法转化为有理数乘法和同底数幂的乘法等。
3、整体代换法 如公式中的字母a、b不仅表示数,也可以表示单项式、多项式。
4、反向思考法 如逆用乘法公式解题等。
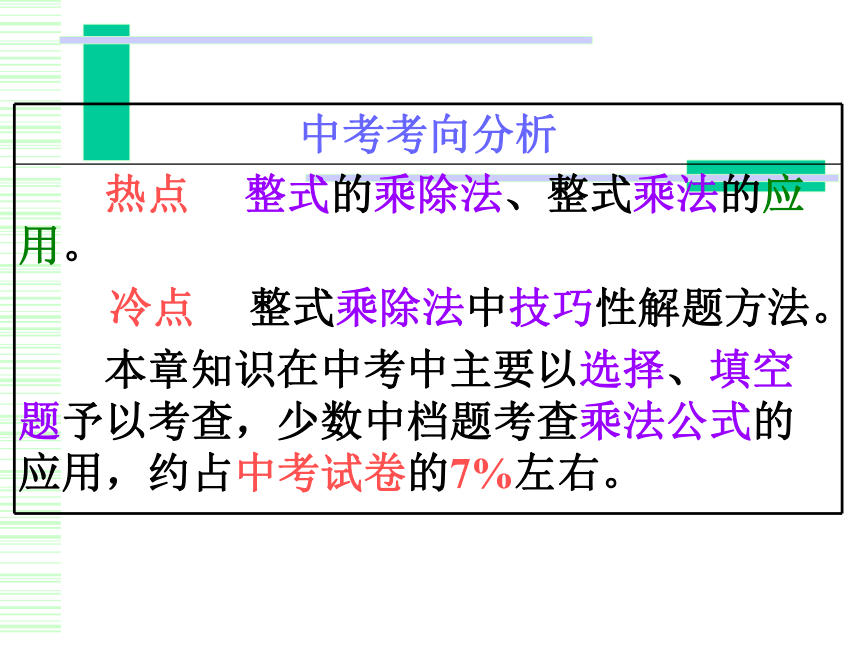
中考考向分析
热点 整式的乘除法、整式乘法的应用。
冷点 整式乘除法中技巧性解题方法。
本章知识在中考中主要以选择、填空题予以考查,少数中档题考查乘法公式的应用,约占中考试卷的7%左右。
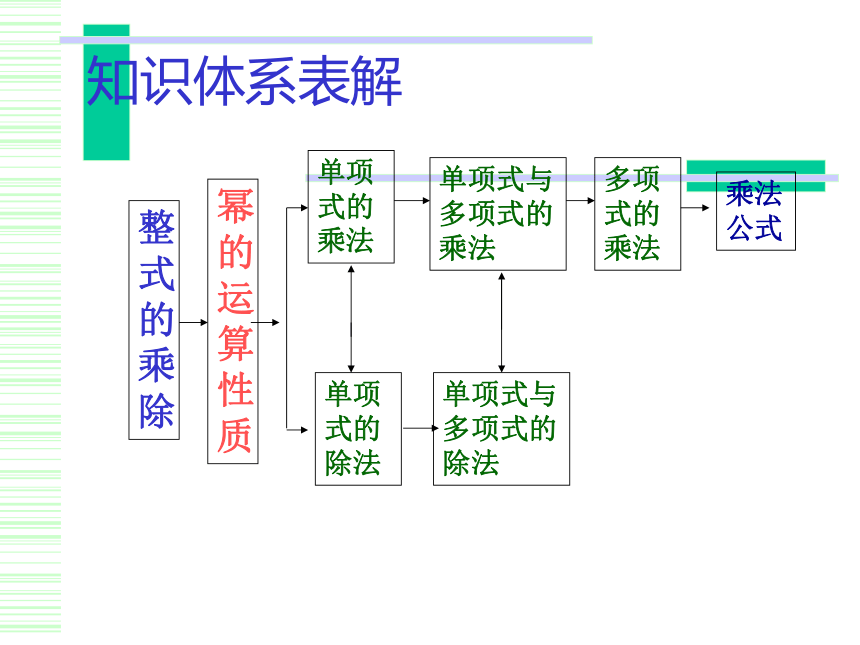
幂的运算性质
整式的乘除
单项式与多项式的乘法
单项式的乘法
多项式的乘法
乘法公式
单项式的除法
单项式与多项式的除法
知识体系表解
同底数幂的乘法
am an=am+n (m、n都是正整数)
(am)n=amn (m、n都是正整数)
幂的乘方
积的乘方
(ab)=an bn (n是正整数)
同底数幂的除法
am ÷an=am-n
(a≠0,m、n都是正整数,m>n)
2、a0=1,(a≠0 )
3、
1、
单项式乘法
单项式相乘,把它们的系数、
相同字母分别相乘,对于只在一
个单项式里出现的字母,则连同
它的指数作为积的一个因式。
多项式乘以单项式
多项式乘以单项式,用
单项式去乘以多项式的每一
项,并把所得的 积 相加。
多项式乘以多项式
多项式乘以多项式,用一
个多项式的每一项去乘以另一
个多项式的每一项,并把所得
的 积 相加。
乘法公式
(x+a)(x+b)=x2+(a+b)x+ab
(a+b)(a-b)=a2-b2
(a±b) =a2± 2ab+b2
单项式的除法
单项式相除,把它们的系数、
同底数幂分别相除,作为商的一
个因式,对于只在被除式里含有
的字母,则连同它的指数作为商
的一个因式。
多项式除以单项式
多项式除以单项式,先
把这个多项式的每一项除以
这个单项式,再把所得的商
相加。
一、判断正误:
A.b5 b5=2b5( ) B.x5+x5=x10 ( )
C.(c3)4 ÷c5=c6 ( )
D.(m3 m2)5÷m4=m21 ( )
二、计算(口答)
1.(-3)2 (-3)3=
2. x3 xn-1-xn-2 x4+xn+2=
3.(m-n)2 (n-m)2 (n-m)3=
4. -(- 2a2b4)3=
5.(-2ab)3 b5 ÷8a2b4=
或-35
xn+2
(n-m)3
-ab4
8a6b12
(-3)5
三、利用乘法公式计算
四、计算
五、求证不论x、y取何值,代数式x2+y2+4x-6y+14的值总是正数。
即原式的值总是正数
证明:
x2+y2+4x-6y+14
= x2+ 4x + 4+y2-6y+9+1
=(x+2)2+(y-3)2+1
∵ (x+2)2≥0,(y-3)2 ≥0
∴ (x+2)2+(y-3)2+1>0
六、若10a=20,10b=5-1,求9a÷32b的值。
解:∵ 10a ÷ 10b=10a-b
∴10a-b=20 ÷ 5-1=100=102
∴ a-b=2
∵ 9a÷32b= 9a ÷ 9b=9a-b
∴ 9a÷32b= 92=81
思考题
1、观察下列各式:
(x-1)(x+1)=x2-1
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
根据前面各式的规律可得
(x-1)(xn+xn-1+ +x+1)=____ (其中n为正整数)
xn+1-1
2、 王老师在一次团体体操队列造型设计中,先让全体队员排成一个方阵(即行与列的人数一样的队形),人数正好够用。然后再进行各种队形变化,其中的一个造型需要5人一组,手执彩带变换图形,在讨论分组方案时,有人说现在的队员人数按“5人一组”分将多出3人,你说这可能吗?为什么?
3、计算
整式的乘除
(复习课)
四川师范大学实验外国语学校
杜林峰
书 山 有 路 勤 为 径,学 海 无 崖 法 作 舟
少 小 不 学 习,老 来 徒 伤 悲
天才就是百分之一的灵感,百分之九十九的汗水!
成功=艰苦的劳动+正确的方法+少谈空话
欢 迎 光 临!欢 迎 指 导!
欢 迎 光 临!欢 迎 指 导!
欢 迎 光 临!欢 迎 指 导!
欢 迎 光 临!欢 迎 指 导!
重难点知识归纳
重点 整式的乘除法,乘法公式的应用
难点 整式乘法公式的应用
要突破上述难点,先要认真掌握好乘法公式的基本结构,再要针对性地加强练习,以达到熟练自如的目的。
知识表解
研究性学习
学习本章知识,先得有较好的转化意识,即善于化新为旧,如把单项式乘法转化为有理数乘法和同底数幂的乘法等,这样,新知识的学习就不难了。
同时要特别逆用一些法则、公式,这样会为解题提供方便、简洁的解法,也锻炼了思维能力。
解题方法技巧
1、归纳法 如本章的一些性质、法则、公式的导出,一般都是由特殊到一般归纳得到的。
2、转化法 如单项式乘法转化为有理数乘法和同底数幂的乘法等。
3、整体代换法 如公式中的字母a、b不仅表示数,也可以表示单项式、多项式。
4、反向思考法 如逆用乘法公式解题等。
中考考向分析
热点 整式的乘除法、整式乘法的应用。
冷点 整式乘除法中技巧性解题方法。
本章知识在中考中主要以选择、填空题予以考查,少数中档题考查乘法公式的应用,约占中考试卷的7%左右。
幂的运算性质
整式的乘除
单项式与多项式的乘法
单项式的乘法
多项式的乘法
乘法公式
单项式的除法
单项式与多项式的除法
知识体系表解
同底数幂的乘法
am an=am+n (m、n都是正整数)
(am)n=amn (m、n都是正整数)
幂的乘方
积的乘方
(ab)=an bn (n是正整数)
同底数幂的除法
am ÷an=am-n
(a≠0,m、n都是正整数,m>n)
2、a0=1,(a≠0 )
3、
1、
单项式乘法
单项式相乘,把它们的系数、
相同字母分别相乘,对于只在一
个单项式里出现的字母,则连同
它的指数作为积的一个因式。
多项式乘以单项式
多项式乘以单项式,用
单项式去乘以多项式的每一
项,并把所得的 积 相加。
多项式乘以多项式
多项式乘以多项式,用一
个多项式的每一项去乘以另一
个多项式的每一项,并把所得
的 积 相加。
乘法公式
(x+a)(x+b)=x2+(a+b)x+ab
(a+b)(a-b)=a2-b2
(a±b) =a2± 2ab+b2
单项式的除法
单项式相除,把它们的系数、
同底数幂分别相除,作为商的一
个因式,对于只在被除式里含有
的字母,则连同它的指数作为商
的一个因式。
多项式除以单项式
多项式除以单项式,先
把这个多项式的每一项除以
这个单项式,再把所得的商
相加。
一、判断正误:
A.b5 b5=2b5( ) B.x5+x5=x10 ( )
C.(c3)4 ÷c5=c6 ( )
D.(m3 m2)5÷m4=m21 ( )
二、计算(口答)
1.(-3)2 (-3)3=
2. x3 xn-1-xn-2 x4+xn+2=
3.(m-n)2 (n-m)2 (n-m)3=
4. -(- 2a2b4)3=
5.(-2ab)3 b5 ÷8a2b4=
或-35
xn+2
(n-m)3
-ab4
8a6b12
(-3)5
三、利用乘法公式计算
四、计算
五、求证不论x、y取何值,代数式x2+y2+4x-6y+14的值总是正数。
即原式的值总是正数
证明:
x2+y2+4x-6y+14
= x2+ 4x + 4+y2-6y+9+1
=(x+2)2+(y-3)2+1
∵ (x+2)2≥0,(y-3)2 ≥0
∴ (x+2)2+(y-3)2+1>0
六、若10a=20,10b=5-1,求9a÷32b的值。
解:∵ 10a ÷ 10b=10a-b
∴10a-b=20 ÷ 5-1=100=102
∴ a-b=2
∵ 9a÷32b= 9a ÷ 9b=9a-b
∴ 9a÷32b= 92=81
思考题
1、观察下列各式:
(x-1)(x+1)=x2-1
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
根据前面各式的规律可得
(x-1)(xn+xn-1+ +x+1)=____ (其中n为正整数)
xn+1-1
2、 王老师在一次团体体操队列造型设计中,先让全体队员排成一个方阵(即行与列的人数一样的队形),人数正好够用。然后再进行各种队形变化,其中的一个造型需要5人一组,手执彩带变换图形,在讨论分组方案时,有人说现在的队员人数按“5人一组”分将多出3人,你说这可能吗?为什么?
3、计算
