人教版九年级上册数学 23.1图形的旋转 同步测试(Word版 含答案)
文档属性
| 名称 | 人教版九年级上册数学 23.1图形的旋转 同步测试(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 144.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-11 00:00:00 | ||
图片预览

文档简介
23.1图形的旋转
同步测试
一.选择题
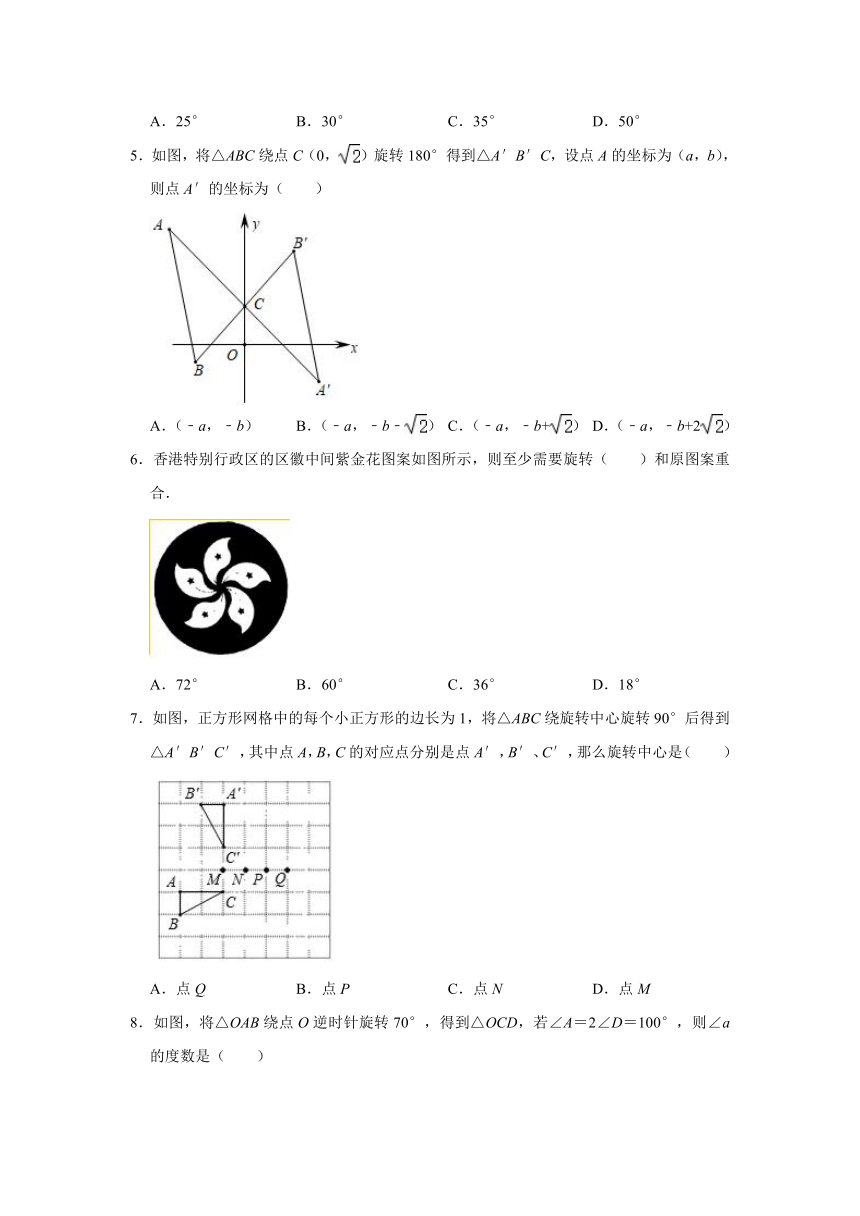
1.如图△ABC绕点A旋转至△ADE,则旋转角是( )
A.∠BAD
B.∠BAC
C.∠BAE
D.∠CAD
2.如图,将Rt△ABC绕着直角顶点C旋转得到△DEC,点A的对应点D恰好是边AB的中点,下列结论错误的是( )
A.AC=CD
B.∠ACD=∠BCE
C.CD:AB=1:2
D.AC:CE=1:
3.如图,图案由三个叶片组成,且其绕点O旋转120°后可以和自身重合,若三个叶片的总面积为12平方厘米,∠AOB=120°,则图中阴影部分的面积之和为( )平方厘米.
A.2
B.4
C.6
D.8
4.如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C逆时针旋转一定的角度得到Rt△A′B′C,此时点A在边B′C上,且∠BCA′=130°,则∠B′的度数为( )
A.25°
B.30°
C.35°
D.50°
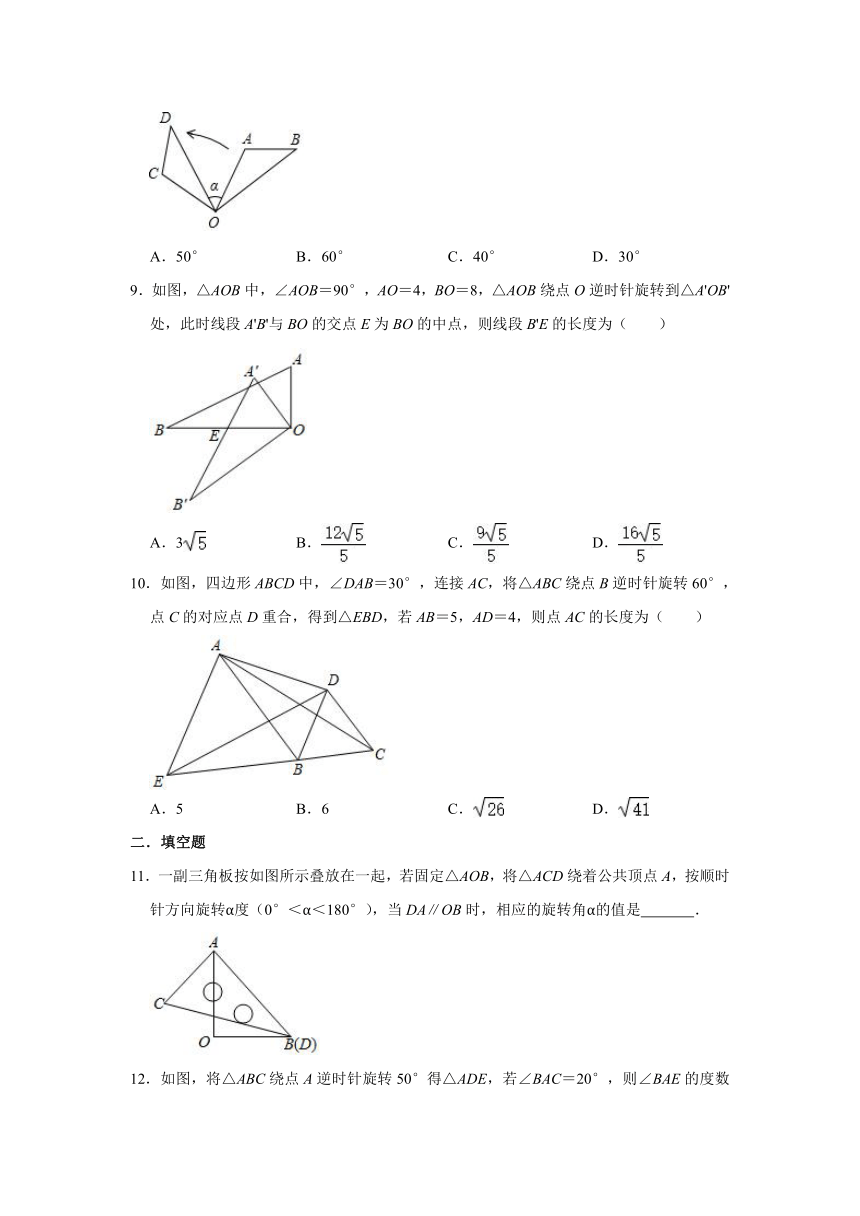
5.如图,将△ABC绕点C(0,)旋转180°得到△A′B′C,设点A的坐标为(a,b),则点A′的坐标为( )
A.(﹣a,﹣b)
B.(﹣a,﹣b﹣)
C.(﹣a,﹣b+)
D.(﹣a,﹣b+2)
6.香港特别行政区的区徽中间紫金花图案如图所示,则至少需要旋转( )和原图案重合.
A.72°
B.60°
C.36°
D.18°
7.如图,正方形网格中的每个小正方形的边长为1,将△ABC绕旋转中心旋转90°后得到△A′B′C′,其中点A,B,C的对应点分别是点A′,B′、C′,那么旋转中心是( )
A.点Q
B.点P
C.点N
D.点M
8.如图,将△OAB绕点O逆时针旋转70°,得到△OCD,若∠A=2∠D=100°,则∠a的度数是( )
A.50°
B.60°
C.40°
D.30°
9.如图,△AOB中,∠AOB=90°,AO=4,BO=8,△AOB绕点O逆时针旋转到△A'OB'处,此时线段A'B'与BO的交点E为BO的中点,则线段B'E的长度为( )
A.3
B.
C.
D.
10.如图,四边形ABCD中,∠DAB=30°,连接AC,将△ABC绕点B逆时针旋转60°,点C的对应点D重合,得到△EBD,若AB=5,AD=4,则点AC的长度为( )
A.5
B.6
C.
D.
二.填空题
11.一副三角板按如图所示叠放在一起,若固定△AOB,将△ACD绕着公共顶点A,按顺时针方向旋转α度(0°<α<180°),当DA∥OB时,相应的旋转角α的值是
.
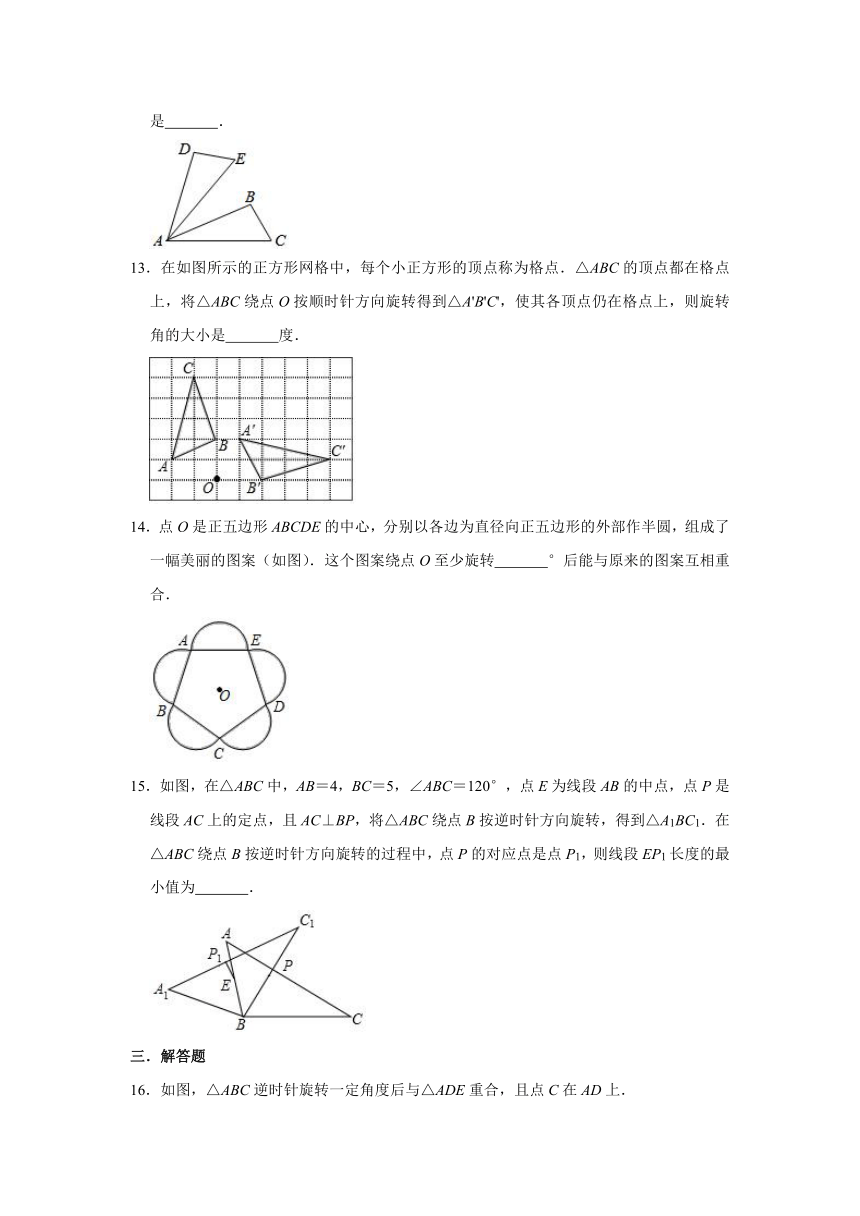
12.如图,将△ABC绕点A逆时针旋转50°得△ADE,若∠BAC=20°,则∠BAE的度数是
.
13.在如图所示的正方形网格中,每个小正方形的顶点称为格点.△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C',使其各顶点仍在格点上,则旋转角的大小是
度.
14.点O是正五边形ABCDE的中心,分别以各边为直径向正五边形的外部作半圆,组成了一幅美丽的图案(如图).这个图案绕点O至少旋转
°后能与原来的图案互相重合.
15.如图,在△ABC中,AB=4,BC=5,∠ABC=120°,点E为线段AB的中点,点P是线段AC上的定点,且AC⊥BP,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.在△ABC绕点B按逆时针方向旋转的过程中,点P的对应点是点P1,则线段EP1长度的最小值为
.
三.解答题
16.如图,△ABC逆时针旋转一定角度后与△ADE重合,且点C在AD上.
(1)指出旋转中心;
(2)若∠B=21°,∠ACB=26°,求出旋转的度数;
(3)若AB=5,CD=3,则AE的长是多少?为什么?
17.如图,P是等边三角形ABC内一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB.求:
(1)PP′的长度;
(2)∠APB的度数.
18.如图,将矩形ABCD绕着点C按顺时针方向旋转得到矩形FECG,使点B落在AD边上的点E处,连结BG交CE于点H,连结BE.
(1)求证:BE平分∠AEC;
(2)取BC中点P,连结PH,求证:PH∥CG;
(3)若BC=2AB=2,求BG的长.
参考答案
1.A
2.D
3.B
4.A
5.D
6.A
7.C
8.C
9.B
10.D
11.135°
12.30°
13.90°
14.72
15.﹣2
16.解:(1)旋转中心为点A;
(2)∵∠B=21°,∠ACB=26°,
∴∠BAC=180°﹣21°﹣26°=133°,
∴旋转的度数为133°;
(3)由旋转性质知:AE=AC,AD=AB,
∴AE=AB﹣CD=2.
17.解:(1)∵△PAC绕点A逆时针旋转后,得到△P′AB,
∴∠PAP′=60°,P′A=PA=6,
∴△APP′是等边三角形,
∴PP′=PA=6;
(2)∵△PAC绕点A逆时针旋转后,得到△P′AB,
∴P′B=PC=10,
∵△APP′是等边三角形,
∴∠APP′=60°,
∵PB2+PP′2=82+62=100,
P′B2=102=100,
∴PB2+PP′2=P′B2,
∴△P′PB是直角三角形,∠BPP′=90°,
∴∠APB=∠APP′+∠BPP′=60°+90°=150°.
18.解:(1)∵矩形ABCD绕着点C按顺时针方向旋转得到矩形FECG,
∴CB=CE,
∴∠EBC=∠BEC,
又∵AD∥BC,
∴∠EBC=∠BEA,
∴∠BEA=∠BEC,
∴BE平分∠AEC;
(2)如图1,过点B作CE的垂线BQ,
∵BE平分∠AEC,BA⊥AE,BQ⊥CE,
∴AB=BQ,
∴CG=BQ,
∵∠BQH=∠GCH=90°,BQ=AB=CG,∠BHQ=∠GHC,
∴△BHQ≌△GHC(AAS),
∴BH=GH,
即点H是BG中点,
又∵点P是BC中点,
∴PH∥CG;
(3)如图2,过点G作BC的垂线GM,
∵BC=2AB=2,
∴BQ=1,
∴∠BCQ=30°,
∵∠ECG=90°,
∴∠GCM=60°,
∴,,
∴.
同步测试
一.选择题
1.如图△ABC绕点A旋转至△ADE,则旋转角是( )
A.∠BAD
B.∠BAC
C.∠BAE
D.∠CAD
2.如图,将Rt△ABC绕着直角顶点C旋转得到△DEC,点A的对应点D恰好是边AB的中点,下列结论错误的是( )
A.AC=CD
B.∠ACD=∠BCE
C.CD:AB=1:2
D.AC:CE=1:
3.如图,图案由三个叶片组成,且其绕点O旋转120°后可以和自身重合,若三个叶片的总面积为12平方厘米,∠AOB=120°,则图中阴影部分的面积之和为( )平方厘米.
A.2
B.4
C.6
D.8
4.如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点C逆时针旋转一定的角度得到Rt△A′B′C,此时点A在边B′C上,且∠BCA′=130°,则∠B′的度数为( )
A.25°
B.30°
C.35°
D.50°
5.如图,将△ABC绕点C(0,)旋转180°得到△A′B′C,设点A的坐标为(a,b),则点A′的坐标为( )
A.(﹣a,﹣b)
B.(﹣a,﹣b﹣)
C.(﹣a,﹣b+)
D.(﹣a,﹣b+2)
6.香港特别行政区的区徽中间紫金花图案如图所示,则至少需要旋转( )和原图案重合.
A.72°
B.60°
C.36°
D.18°
7.如图,正方形网格中的每个小正方形的边长为1,将△ABC绕旋转中心旋转90°后得到△A′B′C′,其中点A,B,C的对应点分别是点A′,B′、C′,那么旋转中心是( )
A.点Q
B.点P
C.点N
D.点M
8.如图,将△OAB绕点O逆时针旋转70°,得到△OCD,若∠A=2∠D=100°,则∠a的度数是( )
A.50°
B.60°
C.40°
D.30°
9.如图,△AOB中,∠AOB=90°,AO=4,BO=8,△AOB绕点O逆时针旋转到△A'OB'处,此时线段A'B'与BO的交点E为BO的中点,则线段B'E的长度为( )
A.3
B.
C.
D.
10.如图,四边形ABCD中,∠DAB=30°,连接AC,将△ABC绕点B逆时针旋转60°,点C的对应点D重合,得到△EBD,若AB=5,AD=4,则点AC的长度为( )
A.5
B.6
C.
D.
二.填空题
11.一副三角板按如图所示叠放在一起,若固定△AOB,将△ACD绕着公共顶点A,按顺时针方向旋转α度(0°<α<180°),当DA∥OB时,相应的旋转角α的值是
.
12.如图,将△ABC绕点A逆时针旋转50°得△ADE,若∠BAC=20°,则∠BAE的度数是
.
13.在如图所示的正方形网格中,每个小正方形的顶点称为格点.△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C',使其各顶点仍在格点上,则旋转角的大小是
度.
14.点O是正五边形ABCDE的中心,分别以各边为直径向正五边形的外部作半圆,组成了一幅美丽的图案(如图).这个图案绕点O至少旋转
°后能与原来的图案互相重合.
15.如图,在△ABC中,AB=4,BC=5,∠ABC=120°,点E为线段AB的中点,点P是线段AC上的定点,且AC⊥BP,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.在△ABC绕点B按逆时针方向旋转的过程中,点P的对应点是点P1,则线段EP1长度的最小值为
.
三.解答题
16.如图,△ABC逆时针旋转一定角度后与△ADE重合,且点C在AD上.
(1)指出旋转中心;
(2)若∠B=21°,∠ACB=26°,求出旋转的度数;
(3)若AB=5,CD=3,则AE的长是多少?为什么?
17.如图,P是等边三角形ABC内一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB.求:
(1)PP′的长度;
(2)∠APB的度数.
18.如图,将矩形ABCD绕着点C按顺时针方向旋转得到矩形FECG,使点B落在AD边上的点E处,连结BG交CE于点H,连结BE.
(1)求证:BE平分∠AEC;
(2)取BC中点P,连结PH,求证:PH∥CG;
(3)若BC=2AB=2,求BG的长.
参考答案
1.A
2.D
3.B
4.A
5.D
6.A
7.C
8.C
9.B
10.D
11.135°
12.30°
13.90°
14.72
15.﹣2
16.解:(1)旋转中心为点A;
(2)∵∠B=21°,∠ACB=26°,
∴∠BAC=180°﹣21°﹣26°=133°,
∴旋转的度数为133°;
(3)由旋转性质知:AE=AC,AD=AB,
∴AE=AB﹣CD=2.
17.解:(1)∵△PAC绕点A逆时针旋转后,得到△P′AB,
∴∠PAP′=60°,P′A=PA=6,
∴△APP′是等边三角形,
∴PP′=PA=6;
(2)∵△PAC绕点A逆时针旋转后,得到△P′AB,
∴P′B=PC=10,
∵△APP′是等边三角形,
∴∠APP′=60°,
∵PB2+PP′2=82+62=100,
P′B2=102=100,
∴PB2+PP′2=P′B2,
∴△P′PB是直角三角形,∠BPP′=90°,
∴∠APB=∠APP′+∠BPP′=60°+90°=150°.
18.解:(1)∵矩形ABCD绕着点C按顺时针方向旋转得到矩形FECG,
∴CB=CE,
∴∠EBC=∠BEC,
又∵AD∥BC,
∴∠EBC=∠BEA,
∴∠BEA=∠BEC,
∴BE平分∠AEC;
(2)如图1,过点B作CE的垂线BQ,
∵BE平分∠AEC,BA⊥AE,BQ⊥CE,
∴AB=BQ,
∴CG=BQ,
∵∠BQH=∠GCH=90°,BQ=AB=CG,∠BHQ=∠GHC,
∴△BHQ≌△GHC(AAS),
∴BH=GH,
即点H是BG中点,
又∵点P是BC中点,
∴PH∥CG;
(3)如图2,过点G作BC的垂线GM,
∵BC=2AB=2,
∴BQ=1,
∴∠BCQ=30°,
∵∠ECG=90°,
∴∠GCM=60°,
∴,,
∴.
同课章节目录
