人教版九年级上册数学 22.1.3 二次函数y=a(x-h)2+k的图像和性质 课件(19张)
文档属性
| 名称 | 人教版九年级上册数学 22.1.3 二次函数y=a(x-h)2+k的图像和性质 课件(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 256.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-11 23:08:57 | ||
图片预览





文档简介
(共19张PPT)
二次函数y=a(x-h)2+k的图象和性质
1.进一步熟悉作函数图象的主要步骤,会作函数y=a(x-h)2+k的图象.
2.能正确说出y=a(x-h)2+k的图象的开口方向、对称轴和顶点坐标.
3.掌握抛物线y=a(x-h)2+k的平移规律.
重点:熟悉作函数图象的主要步骤,会作函数y=a(x-h)2+k的图象.
难点:能正确说出y=a(x-h)2+k的图象的开口方向、对称轴和顶点坐标,掌握抛物线y=a(x-h)2+k的平移规律.
教学目标:
二次函数y=a(x-h)2的性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
开口大小
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=a(x-h)2
(a>0)
y=a(x-h)2
(a<0)
(h,0)
(h,0)
直线x=h
直线x=h
在x轴的上方(除顶点外)
在x轴的下方(
除顶点外)
向上
向下
当x=h时,最小值为0.
当x=h时,最大值为0.
在对称轴的左侧,y随着x的增大而减小.
在对称轴的右侧,
y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大.
在对称轴的右侧,
y随着x的增大而减小.
根据图形填表:
在同一坐标系中作出二次函数y=3x2,y=3(x-1)2和y=3(x-1)2+2的图象.
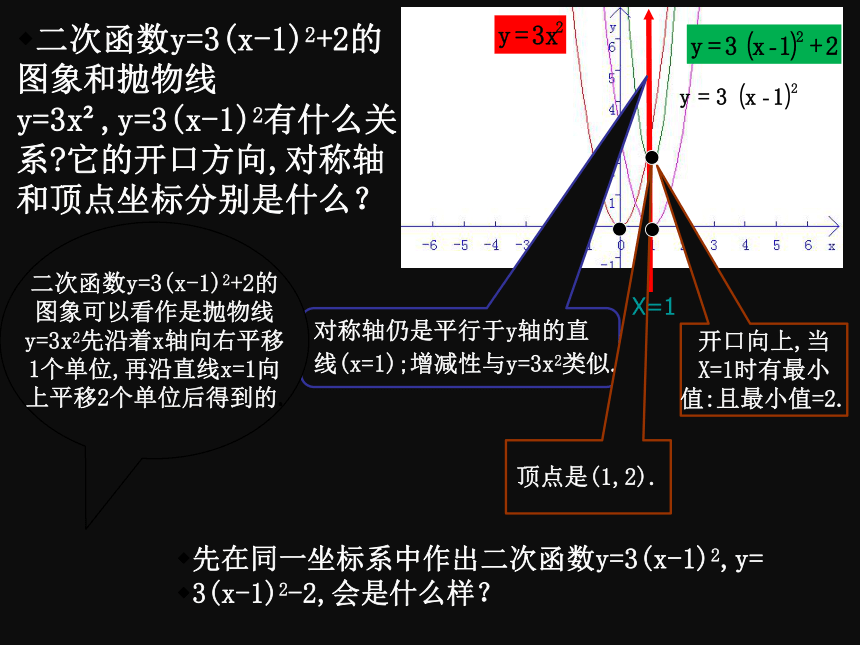
二次函数y=3x2,y=3(x-1)2和y=3(x-1)2+2的图象有什么关系?它们的开口方向,对称轴和顶点坐标分别是什么?作图看一看.
对称轴仍是平行于y轴的直
线(x=1);增减性与y=3x2类似.
顶点是(1,2).
二次函数y=3(x-1)2+2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
上平移2个单位后得到的.
二次函数y=3(x-1)2+2的图象和抛物线y=3x?,y=3(x-1)2有什么关系?它的开口方向,对称轴和顶点坐标分别是什么?
开口向上,当
X=1时有最小
值:且最小值=2.
先在同一坐标系中作出二次函数y=3(x-1)2,y=
3(x-1)2-2,会是什么样?
X=1
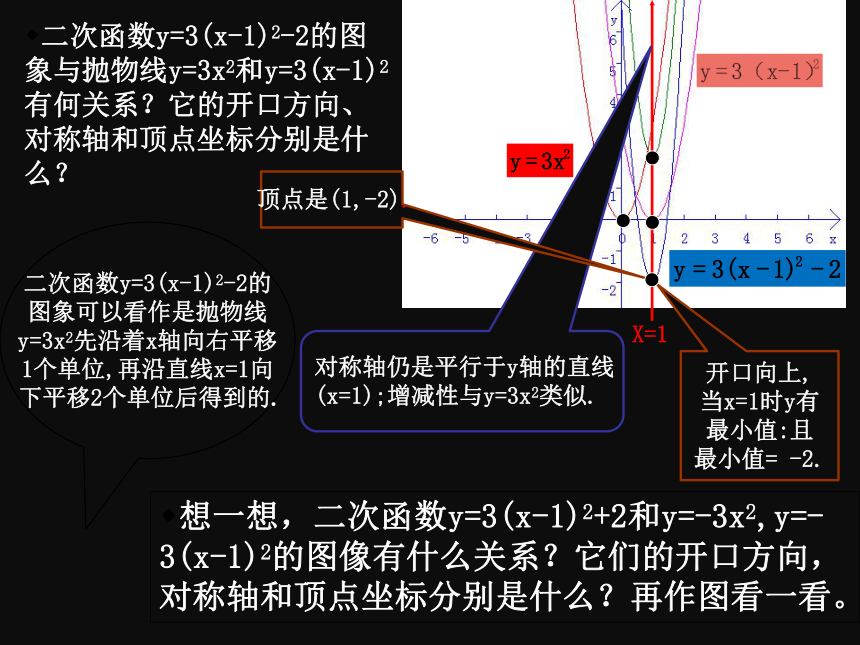
对称轴仍是平行于y轴的直线
(x=1);增减性与y=3x2类似.
顶点是(1,-2).
二次函数y=3(x-1)2-2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
下平移2个单位后得到的.
二次函数y=3(x-1)2-2的图象与抛物线y=3x2和y=3(x-1)2有何关系?它的开口方向、对称轴和顶点坐标分别是什么?
开口向上,
当x=1时y有
最小值:且
最小值=
-2.
想一想,二次函数y=3(x-1)2+2和y=-3x2,y=-3(x-1)2的图像有什么关系?它们的开口方向,对称轴和顶点坐标分别是什么?再作图看一看。
X=1
议一议
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2和y=-3x?,y=-3(x-1)2的图象有什么关系?它们是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?当x取哪些值时,y的值随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小?
对称轴仍是平行于y轴的直线
(x=1);增减性与y=
-3x2类似.
顶点分别是
(1,2)和(1,-2).
二次函数y=-3(x-1)2+2与
y=-3(x-1)2+2的图象可
以看作是抛物线y=-3x2
先沿着x轴向右平移1个
单位,再沿直线x=1向上
(或向下)平移2个单位后
得到的.
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2的图象和抛物线y=-3x?,y=-3(x-1)2有什么关系?
它的开口方向,对称轴和顶点坐标分别是什么?
开口向下,
当x=1时y有
最大值:且
最大值=
2
(或最大值=-2).
想一想,二次函数y=-3(x+1)2+2与y=-3(x+1)2-2的图像和抛物线y=-3x2,y=-3(x+1)2
的图像有什么关系?它们的开口方向,对称轴和顶点坐标分别是什么?再作图看一看。
y
X=1
对称轴仍是平行于y轴的直线
(x=-1);增减性与y=
-3x2类似.
顶点分别是
(-1,2)和(-1,-2)..
二次函数y=-3(x+1)2+2与
y=-3(x+1)2-2的图象可
以看作是抛物线y=-3x2
先沿着x轴向左平移1个
单位,再沿直线x=-1向上
(或向下)平移2个单位后
得到的.
二次函数y=-3(x+1)2+2与y=-3(x+1)2-2的图象和抛物线y=-3x2,y=-3(x+1)2有什么关系?它的开口方向,对称轴和顶点坐标分别是什么?
开口向下,
当x=-1时y有
最大值:且
最大值=
2
(或最大值=-2).
先想一想,再总结二次函数y=a(x-h)2+k的图象和性质.
X=1
二次函数y=a(x-h)2+k的图象和性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
(h,k)
(h,k)
直线x=h
直线x=h
由h和k的符号确定
由h和k的符号确定
向上
向下
当x=h时,最小值为k.
当x=h时,最大值为k.
在对称轴的左侧,y随着x的增大而减小.
在对称轴的右侧,
y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大.
在对称轴的右侧,
y随着x的增大而减小.
根据图形填表:
二次函数y=a(x-h)2+k与y=ax2的关系
y=ax2
(a≠0)
y=ax2+k
(a≠0)
y=a(x-h)2
(a≠0)
y=a(x-h)2+k
(a≠0)
沿对称轴上(下)
平移|k|个单位
沿x轴左(右)
平移|h|个单位
再向左(右)平移|h|个单位
沿对称轴上(下)
平移|k|个单位
注:上正下负,左正右负。
1.指出下列函数图象的开口方向对称轴和顶点坐标:
2.(1)二次函数y=3(x+1)2的图象与二次函数y=3x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?
(2)二次函数y=-3(x-2)2+4的图象与二次函数y=-3x2的图象有什么关系?
对于二次函数y=3(x+1)2,当x取哪些值时,y的值随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小?二次函数y=3(x+1)2+4呢?
随堂练习
1.相同点:
(1)形状相同(图像都是抛物线,开口方向相同).
(2)都是轴对称图形。
(3)都有最(大或小)值。
(4)a>0时,
开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随
x的增大而增大.
a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随
x的增大而减小
。
2.不同点:
只是位置不同(1)顶点不同:分别是(h,k)和(0,0)。
(2)对称轴不同:分别是直线x=
h和y轴。
(2)最值不同:分别是k和0。
3.联系:
y=a(x-h)?+k(a≠0)
的图象可以看成y=ax?的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体上(下)平移|k|个单位
(当k>0时向上平移;当k<0时,向下平移)得到的。
小结
拓展
回味无穷
二次函数y=a(x-h)2+k与y=ax2的关系
1、抛物线y=-2(x+3)?-1的开口向(
),对称轴为(
),顶点坐标为(
),x(
)时,y随x的增大而增大。
2、二次函数
化为y=a(x-h)2+k的形式是(
)
3、抛物线y=3x2先向上平移2个单位,后向右平移3个单位,所得到的抛物线是(
)
A、y=3(x+3)2-2
B、
y=3(x+3)2+2
C、y=3(x-3)2-2
D、
y=3(x-3)2+2
4、某二次函数的图象向左平移2个单位,然后向上平移3个单位后,得到的函数表达式是y=2x?,
则原函数表达式是(
)。
下
x=-3
(-3,-1)
<
-3
A
D
y=2(x-2)2-3
练习
1.指出下列函数图象的开口方向,对称轴和顶点坐标.必要时作出草图进行验证.
2.填写下表:
y=a(x-h)2+k
开口方向
对称轴
顶点坐标
a>0
a<0
5、如图,抛物线的顶点P的坐标是(1,-3),
则此抛物线对应的二次函数有(
)
A、最大值1
B、最小值-3
C、最大值-3
D、最小值1
6、已知二次函数y=a(x+1)?+c的图象如图所示,
则函数y=ax+c的图象只可能是图中的(
)
A
B
C
D
B
C
如图,△ABC是等腰直角三角形,
D为斜边BC上的一点(D与B、C均不重合),以AD为边作等腰直角三角形ADE,连接CE,设BD=x。
(1)求证:△ABD≌△ACE;
(2)求证:CE⊥BC;
(3)当x取何值时,△DCE的面积最大,最大面积是多少?
A
B
D
C
E
互动探究,拓展延伸
心理学家发现,学生对概念的接受能力y与提出概念所用的时间(单位:min)之间满足函数关系y=
-0.1x?+2.6x+43(0≤x
≤30),y值越大,表示接受能力越强。(1)x在什么范围内,学生的接受能力逐步增强?x在什么范围内,学生的接受能力逐步降低?
(2)第10min时,学生的接受能力是多少?
(
3)多长时间时,学生的接受能力最强?
(1)当0≤x
≤13时,
学生的接受能力逐步增强;当13≤x
≤30时,
学生的接受能力逐步降低。
(2)当x=10时,y=59。
(3)当x=13时,学生的接受能力最强为59.9。
解:
y=
-
0.1(x-13)?+59.9
课堂小结:
二次函数y=a(x-h)2+k的图象画法及其性质的总结;平移的规律。所用的思想方法:从特殊到一般。
二次函数y=a(x-h)2+k的图象和性质
1.进一步熟悉作函数图象的主要步骤,会作函数y=a(x-h)2+k的图象.
2.能正确说出y=a(x-h)2+k的图象的开口方向、对称轴和顶点坐标.
3.掌握抛物线y=a(x-h)2+k的平移规律.
重点:熟悉作函数图象的主要步骤,会作函数y=a(x-h)2+k的图象.
难点:能正确说出y=a(x-h)2+k的图象的开口方向、对称轴和顶点坐标,掌握抛物线y=a(x-h)2+k的平移规律.
教学目标:
二次函数y=a(x-h)2的性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
开口大小
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=a(x-h)2
(a>0)
y=a(x-h)2
(a<0)
(h,0)
(h,0)
直线x=h
直线x=h
在x轴的上方(除顶点外)
在x轴的下方(
除顶点外)
向上
向下
当x=h时,最小值为0.
当x=h时,最大值为0.
在对称轴的左侧,y随着x的增大而减小.
在对称轴的右侧,
y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大.
在对称轴的右侧,
y随着x的增大而减小.
根据图形填表:
在同一坐标系中作出二次函数y=3x2,y=3(x-1)2和y=3(x-1)2+2的图象.
二次函数y=3x2,y=3(x-1)2和y=3(x-1)2+2的图象有什么关系?它们的开口方向,对称轴和顶点坐标分别是什么?作图看一看.
对称轴仍是平行于y轴的直
线(x=1);增减性与y=3x2类似.
顶点是(1,2).
二次函数y=3(x-1)2+2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
上平移2个单位后得到的.
二次函数y=3(x-1)2+2的图象和抛物线y=3x?,y=3(x-1)2有什么关系?它的开口方向,对称轴和顶点坐标分别是什么?
开口向上,当
X=1时有最小
值:且最小值=2.
先在同一坐标系中作出二次函数y=3(x-1)2,y=
3(x-1)2-2,会是什么样?
X=1
对称轴仍是平行于y轴的直线
(x=1);增减性与y=3x2类似.
顶点是(1,-2).
二次函数y=3(x-1)2-2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
下平移2个单位后得到的.
二次函数y=3(x-1)2-2的图象与抛物线y=3x2和y=3(x-1)2有何关系?它的开口方向、对称轴和顶点坐标分别是什么?
开口向上,
当x=1时y有
最小值:且
最小值=
-2.
想一想,二次函数y=3(x-1)2+2和y=-3x2,y=-3(x-1)2的图像有什么关系?它们的开口方向,对称轴和顶点坐标分别是什么?再作图看一看。
X=1
议一议
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2和y=-3x?,y=-3(x-1)2的图象有什么关系?它们是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?当x取哪些值时,y的值随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小?
对称轴仍是平行于y轴的直线
(x=1);增减性与y=
-3x2类似.
顶点分别是
(1,2)和(1,-2).
二次函数y=-3(x-1)2+2与
y=-3(x-1)2+2的图象可
以看作是抛物线y=-3x2
先沿着x轴向右平移1个
单位,再沿直线x=1向上
(或向下)平移2个单位后
得到的.
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2的图象和抛物线y=-3x?,y=-3(x-1)2有什么关系?
它的开口方向,对称轴和顶点坐标分别是什么?
开口向下,
当x=1时y有
最大值:且
最大值=
2
(或最大值=-2).
想一想,二次函数y=-3(x+1)2+2与y=-3(x+1)2-2的图像和抛物线y=-3x2,y=-3(x+1)2
的图像有什么关系?它们的开口方向,对称轴和顶点坐标分别是什么?再作图看一看。
y
X=1
对称轴仍是平行于y轴的直线
(x=-1);增减性与y=
-3x2类似.
顶点分别是
(-1,2)和(-1,-2)..
二次函数y=-3(x+1)2+2与
y=-3(x+1)2-2的图象可
以看作是抛物线y=-3x2
先沿着x轴向左平移1个
单位,再沿直线x=-1向上
(或向下)平移2个单位后
得到的.
二次函数y=-3(x+1)2+2与y=-3(x+1)2-2的图象和抛物线y=-3x2,y=-3(x+1)2有什么关系?它的开口方向,对称轴和顶点坐标分别是什么?
开口向下,
当x=-1时y有
最大值:且
最大值=
2
(或最大值=-2).
先想一想,再总结二次函数y=a(x-h)2+k的图象和性质.
X=1
二次函数y=a(x-h)2+k的图象和性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
(h,k)
(h,k)
直线x=h
直线x=h
由h和k的符号确定
由h和k的符号确定
向上
向下
当x=h时,最小值为k.
当x=h时,最大值为k.
在对称轴的左侧,y随着x的增大而减小.
在对称轴的右侧,
y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大.
在对称轴的右侧,
y随着x的增大而减小.
根据图形填表:
二次函数y=a(x-h)2+k与y=ax2的关系
y=ax2
(a≠0)
y=ax2+k
(a≠0)
y=a(x-h)2
(a≠0)
y=a(x-h)2+k
(a≠0)
沿对称轴上(下)
平移|k|个单位
沿x轴左(右)
平移|h|个单位
再向左(右)平移|h|个单位
沿对称轴上(下)
平移|k|个单位
注:上正下负,左正右负。
1.指出下列函数图象的开口方向对称轴和顶点坐标:
2.(1)二次函数y=3(x+1)2的图象与二次函数y=3x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?
(2)二次函数y=-3(x-2)2+4的图象与二次函数y=-3x2的图象有什么关系?
对于二次函数y=3(x+1)2,当x取哪些值时,y的值随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小?二次函数y=3(x+1)2+4呢?
随堂练习
1.相同点:
(1)形状相同(图像都是抛物线,开口方向相同).
(2)都是轴对称图形。
(3)都有最(大或小)值。
(4)a>0时,
开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随
x的增大而增大.
a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随
x的增大而减小
。
2.不同点:
只是位置不同(1)顶点不同:分别是(h,k)和(0,0)。
(2)对称轴不同:分别是直线x=
h和y轴。
(2)最值不同:分别是k和0。
3.联系:
y=a(x-h)?+k(a≠0)
的图象可以看成y=ax?的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体上(下)平移|k|个单位
(当k>0时向上平移;当k<0时,向下平移)得到的。
小结
拓展
回味无穷
二次函数y=a(x-h)2+k与y=ax2的关系
1、抛物线y=-2(x+3)?-1的开口向(
),对称轴为(
),顶点坐标为(
),x(
)时,y随x的增大而增大。
2、二次函数
化为y=a(x-h)2+k的形式是(
)
3、抛物线y=3x2先向上平移2个单位,后向右平移3个单位,所得到的抛物线是(
)
A、y=3(x+3)2-2
B、
y=3(x+3)2+2
C、y=3(x-3)2-2
D、
y=3(x-3)2+2
4、某二次函数的图象向左平移2个单位,然后向上平移3个单位后,得到的函数表达式是y=2x?,
则原函数表达式是(
)。
下
x=-3
(-3,-1)
<
-3
A
D
y=2(x-2)2-3
练习
1.指出下列函数图象的开口方向,对称轴和顶点坐标.必要时作出草图进行验证.
2.填写下表:
y=a(x-h)2+k
开口方向
对称轴
顶点坐标
a>0
a<0
5、如图,抛物线的顶点P的坐标是(1,-3),
则此抛物线对应的二次函数有(
)
A、最大值1
B、最小值-3
C、最大值-3
D、最小值1
6、已知二次函数y=a(x+1)?+c的图象如图所示,
则函数y=ax+c的图象只可能是图中的(
)
A
B
C
D
B
C
如图,△ABC是等腰直角三角形,
D为斜边BC上的一点(D与B、C均不重合),以AD为边作等腰直角三角形ADE,连接CE,设BD=x。
(1)求证:△ABD≌△ACE;
(2)求证:CE⊥BC;
(3)当x取何值时,△DCE的面积最大,最大面积是多少?
A
B
D
C
E
互动探究,拓展延伸
心理学家发现,学生对概念的接受能力y与提出概念所用的时间(单位:min)之间满足函数关系y=
-0.1x?+2.6x+43(0≤x
≤30),y值越大,表示接受能力越强。(1)x在什么范围内,学生的接受能力逐步增强?x在什么范围内,学生的接受能力逐步降低?
(2)第10min时,学生的接受能力是多少?
(
3)多长时间时,学生的接受能力最强?
(1)当0≤x
≤13时,
学生的接受能力逐步增强;当13≤x
≤30时,
学生的接受能力逐步降低。
(2)当x=10时,y=59。
(3)当x=13时,学生的接受能力最强为59.9。
解:
y=
-
0.1(x-13)?+59.9
课堂小结:
二次函数y=a(x-h)2+k的图象画法及其性质的总结;平移的规律。所用的思想方法:从特殊到一般。
同课章节目录
