人教版数学七年级上册 4.3.1角课件(17张)
文档属性
| 名称 | 人教版数学七年级上册 4.3.1角课件(17张) |  | |
| 格式 | zip | ||
| 文件大小 | 855.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-11 23:18:08 | ||
图片预览



文档简介
(共17张PPT)
角
新知引入
观察左边的实物,你发现这些实物能抽象出什么样的共同形象?
——角
新知讲解
角的定义与表示方法
你会画角吗?
问题
从你刚画的这些不同的图形中,能归纳出它们的共同特点吗?尝试去描述一下角是由什么组成的图形?
两条射线
公共端点
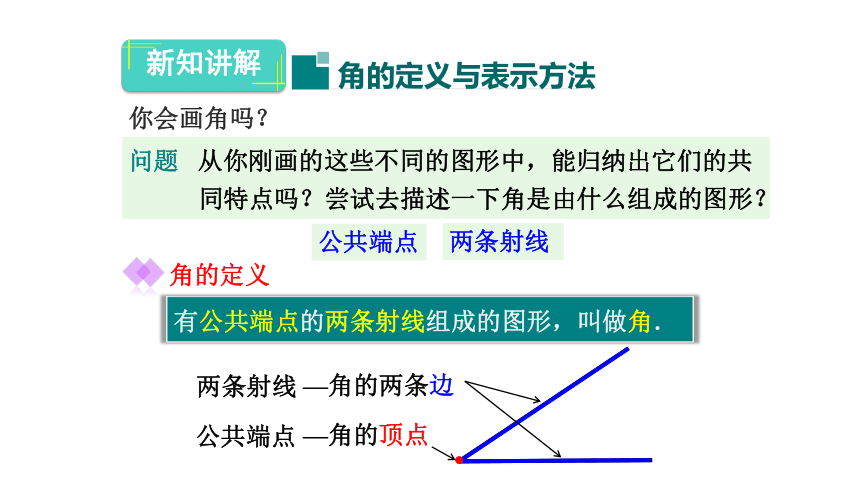
有公共端点的两条射线组成的图形,叫做角.
公共端点
—角的顶点
两条射线
—角的两条边
角的定义
表示顶点的字母一定写在中间.
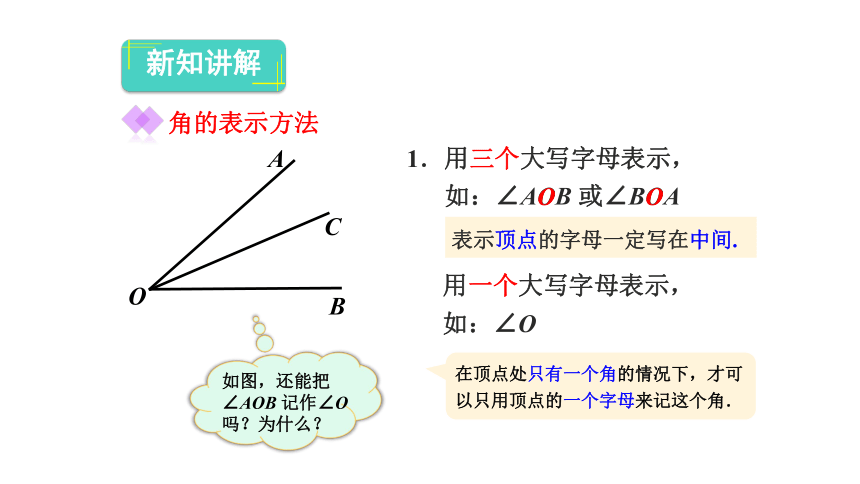
1.用三个大写字母表示,
如:∠AOB
或∠BOA
A
B
O
用一个大写字母表示,
如:∠O
如图,还能把∠AOB
记作∠O
吗?为什么?
在顶点处只有一个角的情况下,才可以只用顶点的一个字母来记这个角.
C
O
新知讲解
角的表示方法
O
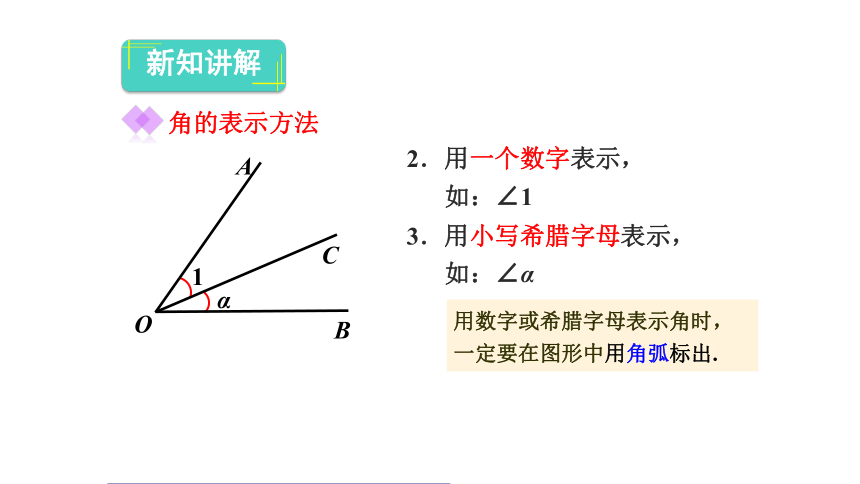
2.用一个数字表示,
如:∠1
3.用小写希腊字母表示,
如:∠α
α
1
A
B
O
C
新知讲解
角的表示方法
用数字或希腊字母表示角时,一定要在图形中用角弧标出.
C
A
B
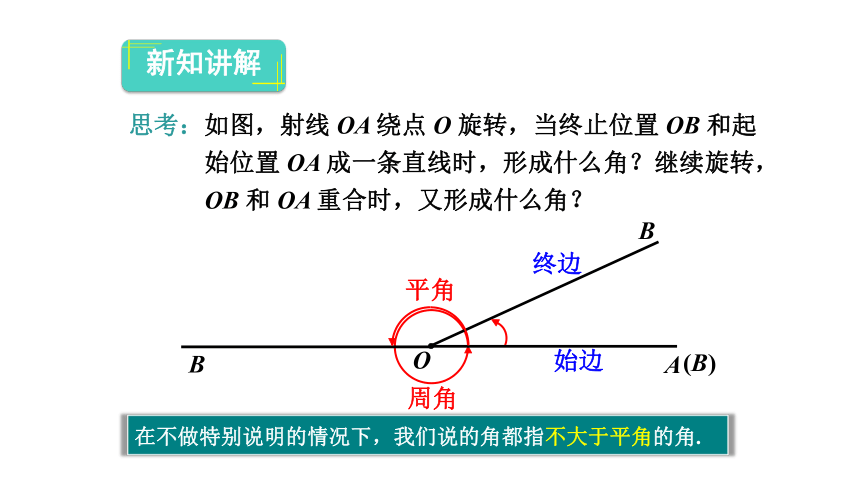
角也可以看作由一条射线绕着它的端点旋转而形成的图形.
始边
终边
O
A
B
(B)
平角
周角
思考:如图,射线
OA
绕点
O
旋转,当终止位置
OB
和起始位置
OA
成一条直线时,形成什么角?继续旋转,OB
和
OA
重合时,又形成什么角?
新知讲解
B
在不做特别说明的情况下,我们说的角都指不大于平角的角.
例1
判断下列哪些图形是角:
(
)
(
)
(
)
(
)
√
×
√
√
新知应用
例2
下列说法正确的是(
)
A.平角是一条直线
B.一条射线是一个周角
C.两条射线组成的图形叫做角
D.两边成一直线的角是平角
新知应用
D
∠1
∠3
∠4
∠ABC
∠ACB
∠BCE
∠5
∠BAC
∠BAD
∠2
2
1
3
4
5
B
A
D
C
E
新知应用
例3
填写下表,将图中的角用不同方法表示出来.
角的度量
角的度量工具:
量角器
问题:怎么知道这个角的大小?
新知讲解
我们常用量角器量角,度、分、秒是常用的角的度量单位.把一个周角
360等分,每一份就是
1
度的角,记作1°;把
1
度的角
60
等分,每一份叫做1
分的角,记作
1′;把1分的角
60等分,每一份叫做1
秒的角,记作1″.
1周角= °;1平角= °.
360
180
1°=
′;1′=
″.
60
60
新知讲解
(1)
57.32°=
°
′
″;
解析:57.32°=57°+0.32×60′
=57°+19.2′
=57°19′+0.2×60″
=57°19′12″
按1°=60′,1′=60″,先把度化成分,再把分化成秒.
(小数化整数)
57
19
12
新知应用
例1
度分秒的互化:
(2)
17°6′36″=
°.
17.11
解析:17°6′36″=17°+6′+
′′
=17?+6.6′
=17?+
°
=17.11?.
新知应用
例1
度分秒的互化:
按1″=
′,1′=
°,先把秒化成分,再把分化成度.
(整数化小数)
例2
如图,时钟显示为10:10时,时针与分针所夹角度(
)
A.90°
B.100°
C.105°
D.115°
解析:时针每小时旋转的夹角360°÷12=30°,
故10分钟,时针旋转的角度为5°,
即10:10时,时针与分针所夹角度为4×30°-5°=115°.
D
新知应用
课堂总结
角的定义
有公共端点的两条射线组成的图形.
一条射线绕着它的端点旋转而形成的图形.
角的表示方法
用三个大写字母或一个大写字母表示.
用一个数字加弧线表示.
用一个小写希腊字母加弧线表示.
角的度量
度量单位:度、分、秒.
1周角=360°
1平角=180°
1°=60′
1′=60″
谢谢聆听
角
新知引入
观察左边的实物,你发现这些实物能抽象出什么样的共同形象?
——角
新知讲解
角的定义与表示方法
你会画角吗?
问题
从你刚画的这些不同的图形中,能归纳出它们的共同特点吗?尝试去描述一下角是由什么组成的图形?
两条射线
公共端点
有公共端点的两条射线组成的图形,叫做角.
公共端点
—角的顶点
两条射线
—角的两条边
角的定义
表示顶点的字母一定写在中间.
1.用三个大写字母表示,
如:∠AOB
或∠BOA
A
B
O
用一个大写字母表示,
如:∠O
如图,还能把∠AOB
记作∠O
吗?为什么?
在顶点处只有一个角的情况下,才可以只用顶点的一个字母来记这个角.
C
O
新知讲解
角的表示方法
O
2.用一个数字表示,
如:∠1
3.用小写希腊字母表示,
如:∠α
α
1
A
B
O
C
新知讲解
角的表示方法
用数字或希腊字母表示角时,一定要在图形中用角弧标出.
C
A
B
角也可以看作由一条射线绕着它的端点旋转而形成的图形.
始边
终边
O
A
B
(B)
平角
周角
思考:如图,射线
OA
绕点
O
旋转,当终止位置
OB
和起始位置
OA
成一条直线时,形成什么角?继续旋转,OB
和
OA
重合时,又形成什么角?
新知讲解
B
在不做特别说明的情况下,我们说的角都指不大于平角的角.
例1
判断下列哪些图形是角:
(
)
(
)
(
)
(
)
√
×
√
√
新知应用
例2
下列说法正确的是(
)
A.平角是一条直线
B.一条射线是一个周角
C.两条射线组成的图形叫做角
D.两边成一直线的角是平角
新知应用
D
∠1
∠3
∠4
∠ABC
∠ACB
∠BCE
∠5
∠BAC
∠BAD
∠2
2
1
3
4
5
B
A
D
C
E
新知应用
例3
填写下表,将图中的角用不同方法表示出来.
角的度量
角的度量工具:
量角器
问题:怎么知道这个角的大小?
新知讲解
我们常用量角器量角,度、分、秒是常用的角的度量单位.把一个周角
360等分,每一份就是
1
度的角,记作1°;把
1
度的角
60
等分,每一份叫做1
分的角,记作
1′;把1分的角
60等分,每一份叫做1
秒的角,记作1″.
1周角= °;1平角= °.
360
180
1°=
′;1′=
″.
60
60
新知讲解
(1)
57.32°=
°
′
″;
解析:57.32°=57°+0.32×60′
=57°+19.2′
=57°19′+0.2×60″
=57°19′12″
按1°=60′,1′=60″,先把度化成分,再把分化成秒.
(小数化整数)
57
19
12
新知应用
例1
度分秒的互化:
(2)
17°6′36″=
°.
17.11
解析:17°6′36″=17°+6′+
′′
=17?+6.6′
=17?+
°
=17.11?.
新知应用
例1
度分秒的互化:
按1″=
′,1′=
°,先把秒化成分,再把分化成度.
(整数化小数)
例2
如图,时钟显示为10:10时,时针与分针所夹角度(
)
A.90°
B.100°
C.105°
D.115°
解析:时针每小时旋转的夹角360°÷12=30°,
故10分钟,时针旋转的角度为5°,
即10:10时,时针与分针所夹角度为4×30°-5°=115°.
D
新知应用
课堂总结
角的定义
有公共端点的两条射线组成的图形.
一条射线绕着它的端点旋转而形成的图形.
角的表示方法
用三个大写字母或一个大写字母表示.
用一个数字加弧线表示.
用一个小写希腊字母加弧线表示.
角的度量
度量单位:度、分、秒.
1周角=360°
1平角=180°
1°=60′
1′=60″
谢谢聆听
