2020年秋人教版九年级上数学课件: 24.2.2 直线和圆的位置关系(17张)
文档属性
| 名称 | 2020年秋人教版九年级上数学课件: 24.2.2 直线和圆的位置关系(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 313.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
葫芦岛第六初级中学
直线与圆的位置关系
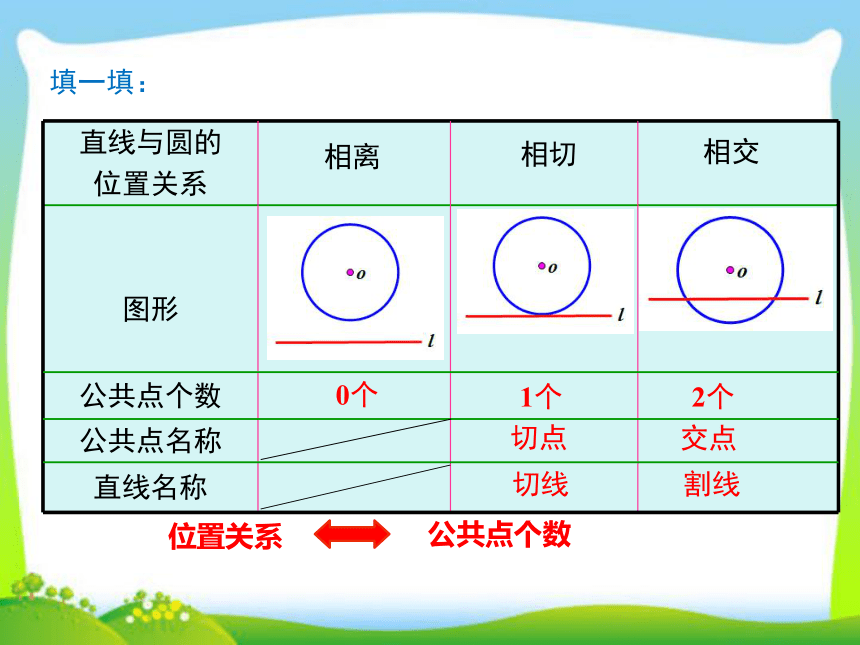
直线与圆的
位置关系
图形
公共点个数
公共点名称
直线名称
2个
交点
割线
1个
切点
切线
0个
相离
相切
相交
位置关系
公共点个数
填一填:
根据上面观察的发现结果,你认为直线与圆的位置关系可以分为几类?你分类的依据是什么?分别把它们的图形在草稿纸上画出来.
?
1.已知圆的半径为6cm,设直线和圆心的距离为d
:
(3)若d=8cm
,则直线与圆______,
直线与圆有____个公共点.
(2)若d=6cm
,则直线与圆______,
直线与圆有____个公共点.
(1)若d=4cm
,则直线与圆 ,
直线与圆有____个公共点.
(3)若AB和⊙O相交,则
.
2.已知⊙O的半径为5cm,
圆心O与直线AB的距离为d,
根据条件
填写d的范围:
(1)若AB和⊙O相离,
则
;
(2)若AB和⊙O相切,
则
;
相交
相切
相离
d
>
5cm
d
=
5cm
0cm≤d
<
5cm
2
1
0
练一练:
刚才同学们用直尺在圆上移动的过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
相关知识:
点到直线的距离是指从直线外一点(A)到直线(l)的垂线段(OA)的长度.
l
A
O
直线与圆的位置关系的性质与判定
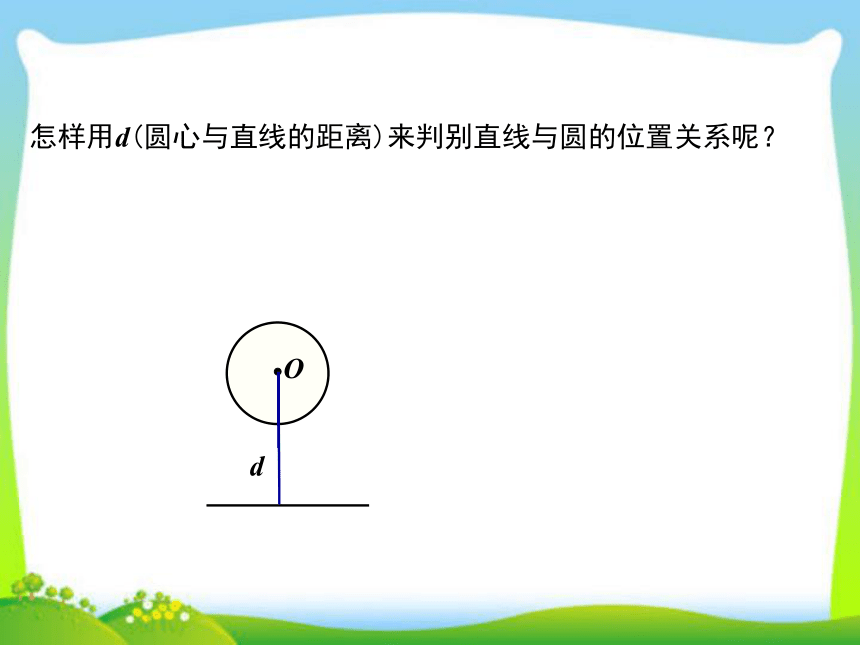
怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢?
O
d
合作探究
直线和圆相交
d<
r
直线和圆相切
d=
r
直线和圆相离
d>
r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
(用圆心O到直线的距离d与圆的半径r的关系来区分)
o
o
o
直线与圆的位置关系
的性质与判定的区别:
位置关系
数量关系.
公共点个数
B
C
A
4
3
在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)
r=2cm;(2)
r=2.4cm;
(3)
r=3cm.
分析:要了解AB与⊙C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出C到AB的距离d.
D
例题
解:过C作CD⊥AB,垂足为D.
在△ABC中,
AB=
5.
根据三角形的面积公式有
∴
即圆心C到AB的距离d=2.4cm.
所以
(1)当r=2cm时,
有d
>r,
因此⊙C和AB相离.
B
C
A
4
3
D
d
记住:斜边上的高等于两直角边的乘积除以斜边.
(2)当r=2.4cm时,有d=r.
因此,⊙C和AB相切.
B
C
A
4
3
D
d
(3)当r=3cm时,有d因此,⊙C和AB相交.
B
C
A
4
3
D
d
.O
.O
.O
.O
.O
1.看图判断直线l与⊙O的位置关系?
(1)
(2)
(3)
(4)
(5)
相离
相交
相切
相交
注意:直线是可以无限延伸的.
相交
2.在Rt△ABC中,∠C=90°,AC=6厘米,BC=8厘米,以C为圆心,为r半径作圆,当r=2厘米
,⊙C与直线AB位置关系是
,当r=4.8厘米,⊙C与直线AB位置关系是
,当r=5厘米,⊙C与直线AB位置关系是
。
3.已知:
⊙O半径为4cm,若直线上一点P与圆心O距离为6cm,那么直线与圆的位置关系是
(
)
A.
相离
B.
相切
C.
相交
D.
无法确定
4.⊙O直径是8,直线l和⊙O相交,圆心O到直线l的距离是d,则d应满足(
)
A.
d<8
B.
4<d<8
C.
0
≤d<4
D.
d>0
相离
相切
相交
D
C
5.直线和圆相交,圆的半径为r,且圆心到直线的距离为5,则有(
)
A.r
<
5
B.
r
>
5
C.
r
=
5
D.
r
≥
5
6.
⊙O的半径为5,直线l上的一点到圆心O的距离是5,则直线l与⊙O的位置关系是(
)
A.
相交或相切
B.
相交或相离
C.
相切或相离
D.
上三种情况都有可能
B
A
已知⊙O的半径r=7cm,直线l1
//
l2,且l1与⊙O相切,圆心O到l2的距离为9cm.求l1与l2的距离.
o
l1
l2
A
B
C
l2
解:(1)
l2与l1在圆的同一侧:
m=9-7=2
(
cm
)
(2)l2与l1在圆的两侧:
m=9+7=16
(
cm
)
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
特别提醒:在图中没有d要先做出该垂线段
相离:0个
相切:1个
相交:2个
相离:d>r
相切:d=r
相交:d0个:相离;1个:相切;2个:相交
d>r:相离
d=r:相切
d课堂总结
葫芦岛第六初级中学
直线与圆的位置关系
直线与圆的
位置关系
图形
公共点个数
公共点名称
直线名称
2个
交点
割线
1个
切点
切线
0个
相离
相切
相交
位置关系
公共点个数
填一填:
根据上面观察的发现结果,你认为直线与圆的位置关系可以分为几类?你分类的依据是什么?分别把它们的图形在草稿纸上画出来.
?
1.已知圆的半径为6cm,设直线和圆心的距离为d
:
(3)若d=8cm
,则直线与圆______,
直线与圆有____个公共点.
(2)若d=6cm
,则直线与圆______,
直线与圆有____个公共点.
(1)若d=4cm
,则直线与圆 ,
直线与圆有____个公共点.
(3)若AB和⊙O相交,则
.
2.已知⊙O的半径为5cm,
圆心O与直线AB的距离为d,
根据条件
填写d的范围:
(1)若AB和⊙O相离,
则
;
(2)若AB和⊙O相切,
则
;
相交
相切
相离
d
>
5cm
d
=
5cm
0cm≤d
<
5cm
2
1
0
练一练:
刚才同学们用直尺在圆上移动的过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
相关知识:
点到直线的距离是指从直线外一点(A)到直线(l)的垂线段(OA)的长度.
l
A
O
直线与圆的位置关系的性质与判定
怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢?
O
d
合作探究
直线和圆相交
d<
r
直线和圆相切
d=
r
直线和圆相离
d>
r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
(用圆心O到直线的距离d与圆的半径r的关系来区分)
o
o
o
直线与圆的位置关系
的性质与判定的区别:
位置关系
数量关系.
公共点个数
B
C
A
4
3
在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)
r=2cm;(2)
r=2.4cm;
(3)
r=3cm.
分析:要了解AB与⊙C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出C到AB的距离d.
D
例题
解:过C作CD⊥AB,垂足为D.
在△ABC中,
AB=
5.
根据三角形的面积公式有
∴
即圆心C到AB的距离d=2.4cm.
所以
(1)当r=2cm时,
有d
>r,
因此⊙C和AB相离.
B
C
A
4
3
D
d
记住:斜边上的高等于两直角边的乘积除以斜边.
(2)当r=2.4cm时,有d=r.
因此,⊙C和AB相切.
B
C
A
4
3
D
d
(3)当r=3cm时,有d
B
C
A
4
3
D
d
.O
.O
.O
.O
.O
1.看图判断直线l与⊙O的位置关系?
(1)
(2)
(3)
(4)
(5)
相离
相交
相切
相交
注意:直线是可以无限延伸的.
相交
2.在Rt△ABC中,∠C=90°,AC=6厘米,BC=8厘米,以C为圆心,为r半径作圆,当r=2厘米
,⊙C与直线AB位置关系是
,当r=4.8厘米,⊙C与直线AB位置关系是
,当r=5厘米,⊙C与直线AB位置关系是
。
3.已知:
⊙O半径为4cm,若直线上一点P与圆心O距离为6cm,那么直线与圆的位置关系是
(
)
A.
相离
B.
相切
C.
相交
D.
无法确定
4.⊙O直径是8,直线l和⊙O相交,圆心O到直线l的距离是d,则d应满足(
)
A.
d<8
B.
4<d<8
C.
0
≤d<4
D.
d>0
相离
相切
相交
D
C
5.直线和圆相交,圆的半径为r,且圆心到直线的距离为5,则有(
)
A.r
<
5
B.
r
>
5
C.
r
=
5
D.
r
≥
5
6.
⊙O的半径为5,直线l上的一点到圆心O的距离是5,则直线l与⊙O的位置关系是(
)
A.
相交或相切
B.
相交或相离
C.
相切或相离
D.
上三种情况都有可能
B
A
已知⊙O的半径r=7cm,直线l1
//
l2,且l1与⊙O相切,圆心O到l2的距离为9cm.求l1与l2的距离.
o
l1
l2
A
B
C
l2
解:(1)
l2与l1在圆的同一侧:
m=9-7=2
(
cm
)
(2)l2与l1在圆的两侧:
m=9+7=16
(
cm
)
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
特别提醒:在图中没有d要先做出该垂线段
相离:0个
相切:1个
相交:2个
相离:d>r
相切:d=r
相交:d
d>r:相离
d=r:相切
d
同课章节目录
