2020-2021学年九年级上册数学23.2.1 中心对称课后提升训练试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年九年级上册数学23.2.1 中心对称课后提升训练试卷(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 395.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-11 00:00:00 | ||
图片预览


文档简介
2020年秋绵阳南山双语学校
初中数学(人教版)九年级
上册
第二十三章 旋转
23.2 中心对称
23.2.1 中心对称
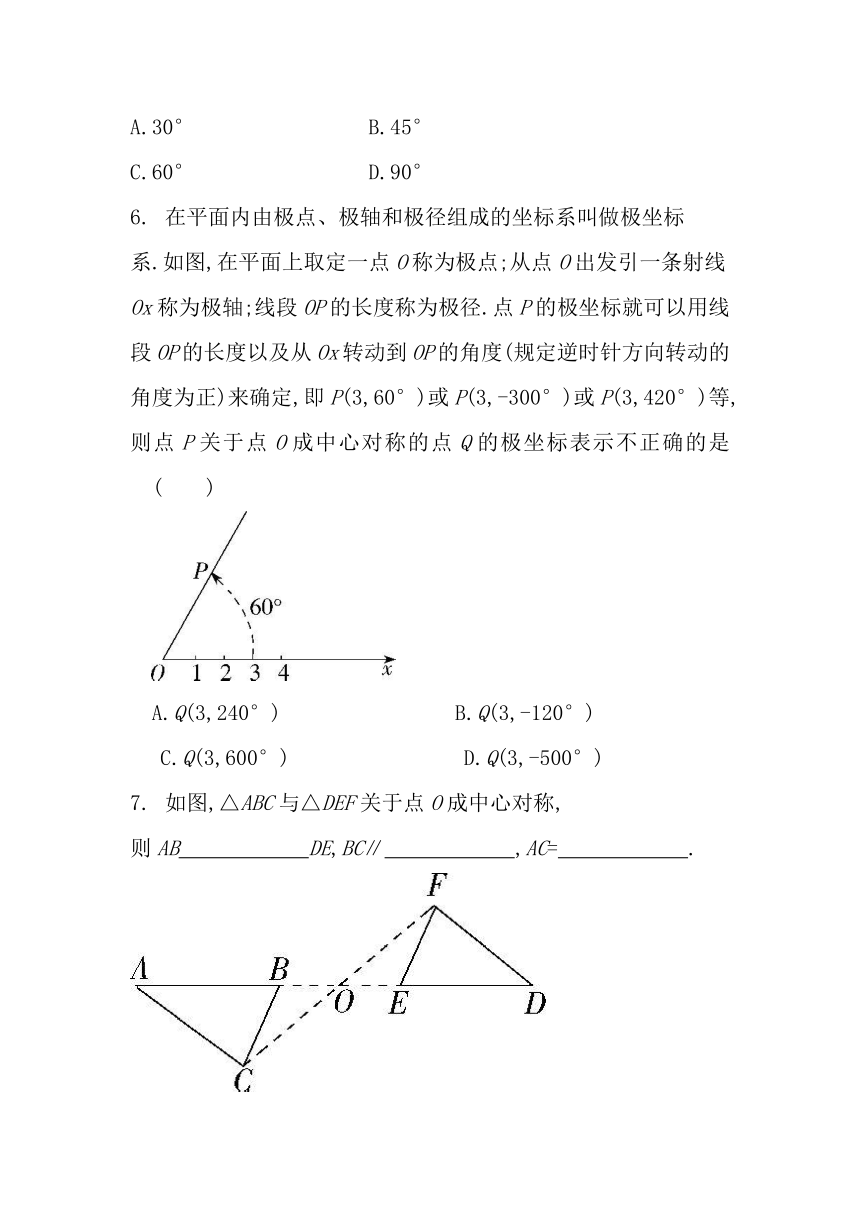
1.(2020河北石家庄裕华模拟)下列图形中,△A‘B’C‘与△ABC成中心对称的是(???)
?
2.如图,△ABC与△DEF成中心对称,则下列关于对称中心的描述不正确的是?( )
A.对称中心是线段BE的中点 ????
B.对称中心是线段FC的中点
C.对称中心是点C
D.对称中心是线段AD与BE的交点
3.
点A和点B的坐标分别为(0,2),(1,0),若将△OAB绕点B顺时针旋转180°后,得到△O'A'B,则点A的对应点A'的坐标是?( )
A.(0,2) ????B.(2,2)
C.(-2,2) ????D.(2,-2)
4.
(2019四川自贡富顺期中)如图,△ABC与△A'B'C'关于点O成中心对称,下列结论中不成立的是?( )
A.OC=OC' ????B.OA=OA'
C.BC=B'C' ????D.∠ABC=∠A'C'B'
5.
(2019山东烟台莱州期末)如图,△ABC中,AB=AC,△ABC与△FEC关于点C成中心对称,连接AE,BF,当四边形ABFE为矩形时,∠ACB的度数为?( )
A.30° ????B.45° ????
C.60° ????D.90°
6.
在平面内由极点、极轴和极径组成的坐标系叫做极坐标
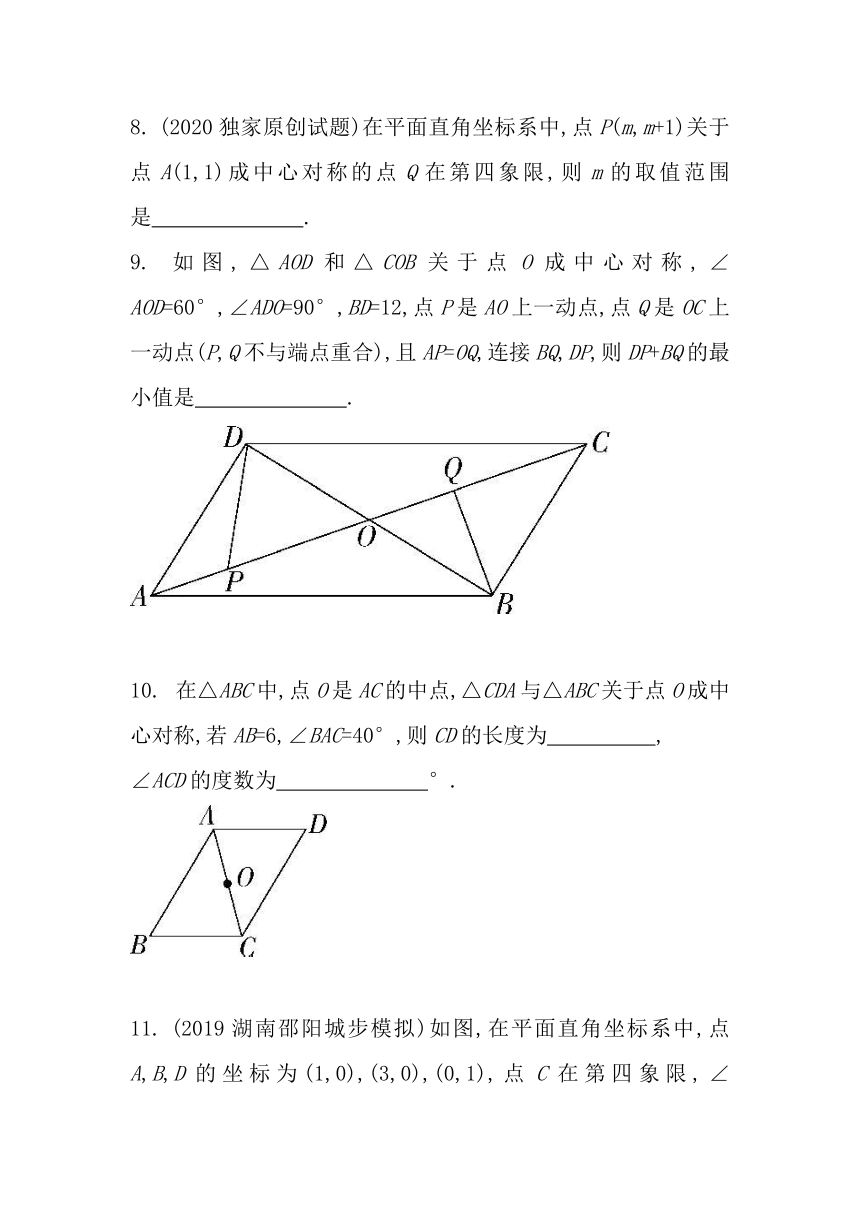
系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动的角度为正)来确定,即P(3,60°)或P(3,-300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是?( )
?
A.Q(3,240°) ????B.Q(3,-120°)
C.Q(3,600°) ????D.Q(3,-500°)
7.
如图,△ABC与△DEF关于点O成中心对称,
则AB ????DE,BC∥ ????,AC= ???.
8.
(2020独家原创试题)在平面直角坐标系中,点P(m,m+1)关于点A(1,1)成中心对称的点Q在第四象限,则m的取值范围是 ????.
9.
如图,△AOD和△COB关于点O成中心对称,∠AOD=60°,∠ADO=90°,BD=12,点P是AO上一动点,点Q是OC上一动点(P,Q不与端点重合),且AP=OQ,连接BQ,DP,则DP+BQ的最小值是 ????.
10.
在△ABC中,点O是AC的中点,△CDA与△ABC关于点O成中心对称,若AB=6,∠BAC=40°,则CD的长度为 ????,
∠ACD的度数为 ????°.
11.
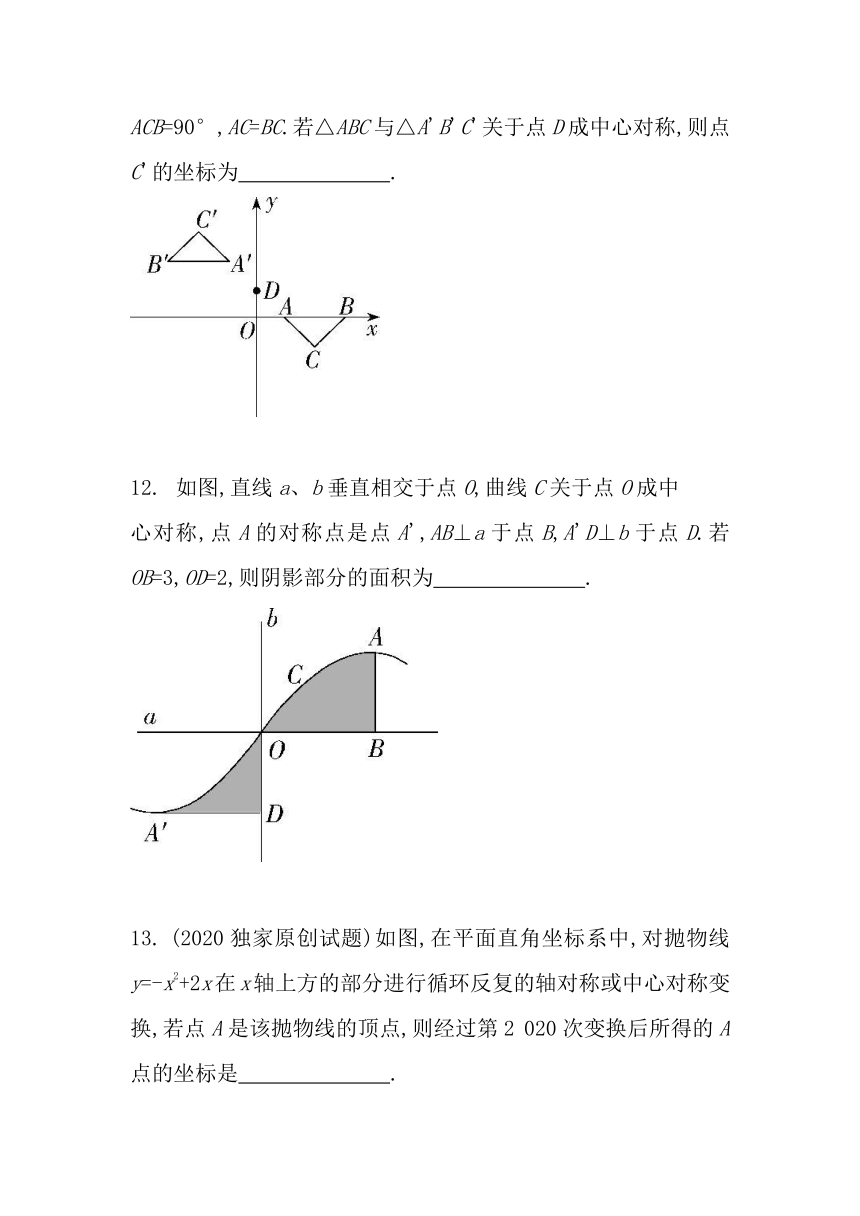
(2019湖南邵阳城步模拟)如图,在平面直角坐标系中,点A,B,D的坐标为(1,0),(3,0),(0,1),点C在第四象限,∠ACB=90°,AC=BC.若△ABC与△A'B'C'关于点D成中心对称,则点C'的坐标为 ????.
12.
如图,直线a、b垂直相交于点O,曲线C关于点O成中
心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积为 ????.
13.
(2020独家原创试题)如图,在平面直角坐标系中,对抛物线y=-x2+2x在x轴上方的部分进行循环反复的轴对称或中心对称变换,若点A是该抛物线的顶点,则经过第2
020次变换后所得的A点的坐标是 ????.
14.
(2019广东潮州期中)如图,在平面直角坐标系中,已知点B(4,2),A(4,0).
(1)画出将△OAB绕原点O逆时针旋转90°后所得的△OA1B1,并写出点A1,B1的坐标;
(2)若点B,B1关于某点成中心对称,则对称中心的坐标为 ????.
15.
(2020山东德州武城期中)如图,△ABC在正方形网格中.
(1)请画出△ABC绕着O逆时针旋转90°后得到的△A1B1C1;
(2)请画出△ABC关于点O对称的△A2B2C2;
(3)在直线MN上求作一点P,使△PAB的周长最小,请画出△PAB.
16.
(2020辽宁抚顺新宾二模,)如图,已知平面直角坐标系中,△ABC的顶点坐标分别为A(1,3),B(2,1),C(4,2).
(1)将△ABC以原点O为旋转中心旋转180°得到△A1B1C1,画出△A1B1C1;
(2)平移△ABC,使点A的对应点A2坐标为(5,-5),画出平移后的△A2B2C2;
(3)若将△A1B1C1绕某一点旋转可得到△A2B2C2,请直接写出这个点的坐标.
17.
如图,在△ABC中,∠A=90°,D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试探索线段BE,EF,FC之间的数量关系.
参考答案
1.
答案????A 根据中心对称的定义知选A.
2.
答案????C △ABC与△DEF成中心对称,点A和D,点B和E,点C和F是对应点,一组对应点连线的中点或两组对应点连线的交点就是对称中心,故选项A、B、D的描述都正确,不符合题意;点C不是对称中心,故选项C描述错误,符合题意.故选C.
3.
答案????D 如图所示,∵点A和点B的坐标分别为(0,2),(1,0),∴OA=2,OB=1,∠AOB=90°.将△OAB绕点B顺时针旋转180°后,得到△O'A'B,∴O'B=OB=1,O'A'=OA=2,
∠A'O'B=90°,∴点A的对应点A'的坐标为(2,-2).
4.
答案????D 对应点的连线被对称中心O平分,A,B中结论正确;成中心对称的两个图形是全等图形,那么对应线段相等,C中结论正确.故选D.
5.
答案????C ∵△ABC与△FEC关于点C成中心对称,∴点B、C、E在同一条直线上,点A、C、F在同一条直线上,CB=CE,CA=CF,∴四边形ABFE为平行四边形,∴当AC=BC时,?ABFE为矩形,而AB=AC,∴此时△ABC为等边三角形,∴当四边形ABFE为矩形时,∠ACB=60°.故选C.
6.
答案????D????由点P与点Q关于点O成中心对称可得,点Q的极坐标为(3,240°)或(3,-120°)或(3,600°)等.故选D.
7.
答案 =;EF;DF
解析 ∵△ABC与△DEF关于点O成中心对称,
∴△ABC≌△DEF,∴AB=DE,AC=DF.
易知△BOC≌△EOF,
∴∠BCO=∠EFO,∴BC∥EF.
8.
答案 19.
答案 12
10.
答案 6;40
解析????∵△CDA与△ABC关于点O成中心对称,且AB=6,∠BAC=40°,∴CD=AB=6,∠ACD=∠BAC=40°.
11.
答案 (-2,3)
12.
答案 6
解析 如图,过A作AE⊥b于点E,∵曲线C关于点O成中心对称,点A的对称点是点A',∴OE=OD=2.根据中心对称的性质,得阴影部分的面积等于矩形ABOE的面积,
∴S阴影=S矩形=2×3=6.
13.
答案 (1,-1)
解析 ∵y=-x2+2x=-(x2-2x)=-(x-1)2+1,∴抛物线y=-x2+2x的顶点A的坐标为(1,1).点A第1次关于x轴对称后在第四象限,第2次关于原点对称后在第二象限,第3次关于y轴对称后在第一象限,回到原始位置,所以每3次对称为一个循环组.∵2
020÷3=673……1,∴经过第2
020次变换后所得的A点与第1次变换后的位置相同,在第四象限,坐标为(1,-1).
14.
解析????(1)如图,△OA1B1即所求,点A1的坐标为(0,4),点B1的坐标为(-2,4).
(2)如图,连接BB1,可知其中点为点(1,3),则点B,B1关于点(1,3)成中心对称,即对称中心的坐标为(1,3).
15.
解析 (1)如图,△A1B1C1为所作.
(2)如图,△A2B2C2为所作.
(3)如图,△PAB为所作.
16.
解析????(1)如图所示,△A1B1C1即所求.
?
(2)如图所示,△A2B2C2即所求.
(3)如图所示,将△A1B1C1绕点P(2,-4)旋转可得到△A2B2C2,即这个点的坐标为(2,-4).
17.
解析????FC2+BE2=EF2.理由如下:
∵D为BC的中点,∴BD=DC.
作△BDE关于点D对称的△CDM,如图所示,
由中心对称的性质可得△BDE≌△CDM.
∴CM=BE,MD=DE,∠DCM=∠B.
又∵∠B+∠ACB=90°,
∴∠DCM+∠ACB=90°,即∠FCM=90°.
连接FM,在△FME中,MD=DE,FD⊥ME,∴FM=FE.
又∵在Rt△FCM中,FC2+CM2=FM2,∴FC2+BE2=EF2.
初中数学(人教版)九年级
上册
第二十三章 旋转
23.2 中心对称
23.2.1 中心对称
1.(2020河北石家庄裕华模拟)下列图形中,△A‘B’C‘与△ABC成中心对称的是(???)
?
2.如图,△ABC与△DEF成中心对称,则下列关于对称中心的描述不正确的是?( )
A.对称中心是线段BE的中点 ????
B.对称中心是线段FC的中点
C.对称中心是点C
D.对称中心是线段AD与BE的交点
3.
点A和点B的坐标分别为(0,2),(1,0),若将△OAB绕点B顺时针旋转180°后,得到△O'A'B,则点A的对应点A'的坐标是?( )
A.(0,2) ????B.(2,2)
C.(-2,2) ????D.(2,-2)
4.
(2019四川自贡富顺期中)如图,△ABC与△A'B'C'关于点O成中心对称,下列结论中不成立的是?( )
A.OC=OC' ????B.OA=OA'
C.BC=B'C' ????D.∠ABC=∠A'C'B'
5.
(2019山东烟台莱州期末)如图,△ABC中,AB=AC,△ABC与△FEC关于点C成中心对称,连接AE,BF,当四边形ABFE为矩形时,∠ACB的度数为?( )
A.30° ????B.45° ????
C.60° ????D.90°
6.
在平面内由极点、极轴和极径组成的坐标系叫做极坐标
系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动的角度为正)来确定,即P(3,60°)或P(3,-300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是?( )
?
A.Q(3,240°) ????B.Q(3,-120°)
C.Q(3,600°) ????D.Q(3,-500°)
7.
如图,△ABC与△DEF关于点O成中心对称,
则AB ????DE,BC∥ ????,AC= ???.
8.
(2020独家原创试题)在平面直角坐标系中,点P(m,m+1)关于点A(1,1)成中心对称的点Q在第四象限,则m的取值范围是 ????.
9.
如图,△AOD和△COB关于点O成中心对称,∠AOD=60°,∠ADO=90°,BD=12,点P是AO上一动点,点Q是OC上一动点(P,Q不与端点重合),且AP=OQ,连接BQ,DP,则DP+BQ的最小值是 ????.
10.
在△ABC中,点O是AC的中点,△CDA与△ABC关于点O成中心对称,若AB=6,∠BAC=40°,则CD的长度为 ????,
∠ACD的度数为 ????°.
11.
(2019湖南邵阳城步模拟)如图,在平面直角坐标系中,点A,B,D的坐标为(1,0),(3,0),(0,1),点C在第四象限,∠ACB=90°,AC=BC.若△ABC与△A'B'C'关于点D成中心对称,则点C'的坐标为 ????.
12.
如图,直线a、b垂直相交于点O,曲线C关于点O成中
心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积为 ????.
13.
(2020独家原创试题)如图,在平面直角坐标系中,对抛物线y=-x2+2x在x轴上方的部分进行循环反复的轴对称或中心对称变换,若点A是该抛物线的顶点,则经过第2
020次变换后所得的A点的坐标是 ????.
14.
(2019广东潮州期中)如图,在平面直角坐标系中,已知点B(4,2),A(4,0).
(1)画出将△OAB绕原点O逆时针旋转90°后所得的△OA1B1,并写出点A1,B1的坐标;
(2)若点B,B1关于某点成中心对称,则对称中心的坐标为 ????.
15.
(2020山东德州武城期中)如图,△ABC在正方形网格中.
(1)请画出△ABC绕着O逆时针旋转90°后得到的△A1B1C1;
(2)请画出△ABC关于点O对称的△A2B2C2;
(3)在直线MN上求作一点P,使△PAB的周长最小,请画出△PAB.
16.
(2020辽宁抚顺新宾二模,)如图,已知平面直角坐标系中,△ABC的顶点坐标分别为A(1,3),B(2,1),C(4,2).
(1)将△ABC以原点O为旋转中心旋转180°得到△A1B1C1,画出△A1B1C1;
(2)平移△ABC,使点A的对应点A2坐标为(5,-5),画出平移后的△A2B2C2;
(3)若将△A1B1C1绕某一点旋转可得到△A2B2C2,请直接写出这个点的坐标.
17.
如图,在△ABC中,∠A=90°,D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试探索线段BE,EF,FC之间的数量关系.
参考答案
1.
答案????A 根据中心对称的定义知选A.
2.
答案????C △ABC与△DEF成中心对称,点A和D,点B和E,点C和F是对应点,一组对应点连线的中点或两组对应点连线的交点就是对称中心,故选项A、B、D的描述都正确,不符合题意;点C不是对称中心,故选项C描述错误,符合题意.故选C.
3.
答案????D 如图所示,∵点A和点B的坐标分别为(0,2),(1,0),∴OA=2,OB=1,∠AOB=90°.将△OAB绕点B顺时针旋转180°后,得到△O'A'B,∴O'B=OB=1,O'A'=OA=2,
∠A'O'B=90°,∴点A的对应点A'的坐标为(2,-2).
4.
答案????D 对应点的连线被对称中心O平分,A,B中结论正确;成中心对称的两个图形是全等图形,那么对应线段相等,C中结论正确.故选D.
5.
答案????C ∵△ABC与△FEC关于点C成中心对称,∴点B、C、E在同一条直线上,点A、C、F在同一条直线上,CB=CE,CA=CF,∴四边形ABFE为平行四边形,∴当AC=BC时,?ABFE为矩形,而AB=AC,∴此时△ABC为等边三角形,∴当四边形ABFE为矩形时,∠ACB=60°.故选C.
6.
答案????D????由点P与点Q关于点O成中心对称可得,点Q的极坐标为(3,240°)或(3,-120°)或(3,600°)等.故选D.
7.
答案 =;EF;DF
解析 ∵△ABC与△DEF关于点O成中心对称,
∴△ABC≌△DEF,∴AB=DE,AC=DF.
易知△BOC≌△EOF,
∴∠BCO=∠EFO,∴BC∥EF.
8.
答案 1
答案 12
10.
答案 6;40
解析????∵△CDA与△ABC关于点O成中心对称,且AB=6,∠BAC=40°,∴CD=AB=6,∠ACD=∠BAC=40°.
11.
答案 (-2,3)
12.
答案 6
解析 如图,过A作AE⊥b于点E,∵曲线C关于点O成中心对称,点A的对称点是点A',∴OE=OD=2.根据中心对称的性质,得阴影部分的面积等于矩形ABOE的面积,
∴S阴影=S矩形=2×3=6.
13.
答案 (1,-1)
解析 ∵y=-x2+2x=-(x2-2x)=-(x-1)2+1,∴抛物线y=-x2+2x的顶点A的坐标为(1,1).点A第1次关于x轴对称后在第四象限,第2次关于原点对称后在第二象限,第3次关于y轴对称后在第一象限,回到原始位置,所以每3次对称为一个循环组.∵2
020÷3=673……1,∴经过第2
020次变换后所得的A点与第1次变换后的位置相同,在第四象限,坐标为(1,-1).
14.
解析????(1)如图,△OA1B1即所求,点A1的坐标为(0,4),点B1的坐标为(-2,4).
(2)如图,连接BB1,可知其中点为点(1,3),则点B,B1关于点(1,3)成中心对称,即对称中心的坐标为(1,3).
15.
解析 (1)如图,△A1B1C1为所作.
(2)如图,△A2B2C2为所作.
(3)如图,△PAB为所作.
16.
解析????(1)如图所示,△A1B1C1即所求.
?
(2)如图所示,△A2B2C2即所求.
(3)如图所示,将△A1B1C1绕点P(2,-4)旋转可得到△A2B2C2,即这个点的坐标为(2,-4).
17.
解析????FC2+BE2=EF2.理由如下:
∵D为BC的中点,∴BD=DC.
作△BDE关于点D对称的△CDM,如图所示,
由中心对称的性质可得△BDE≌△CDM.
∴CM=BE,MD=DE,∠DCM=∠B.
又∵∠B+∠ACB=90°,
∴∠DCM+∠ACB=90°,即∠FCM=90°.
连接FM,在△FME中,MD=DE,FD⊥ME,∴FM=FE.
又∵在Rt△FCM中,FC2+CM2=FM2,∴FC2+BE2=EF2.
同课章节目录
