人教版数学七年级上册1.5有理数的乘方课件(24张)
文档属性
| 名称 | 人教版数学七年级上册1.5有理数的乘方课件(24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 738.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
有理数的乘方
从前有个人发明了国际象棋,他的国王知道后很高兴,问他想要什么赏赐,发明国际象棋的人笑了笑,对国王说,大王只要在棋盘的第一个格子放一粒米,以后每格里面都放前面一格两倍的数量,把64个格子放满就可以了.国王听后哈哈大笑,对他说,这个简单,于是命人拿来棋盘,然后开始在棋盘上放米,1粒、2粒、4粒、8粒……,几天过后,国王发现棋盘还没有放满,而自己国家的粮库里已经没有多少米了……
,
国王这才知道自己太小看这个棋盘.
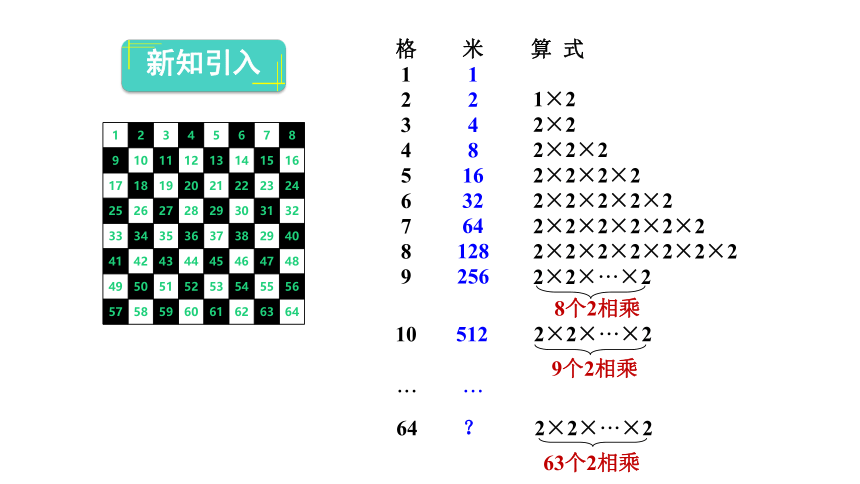
新知引入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
29
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
格
米
算
式
1
1
2
2
3
4
1×2
2×2
4
8
2×2×2
5
16
2×2×2×2
6
32
2×2×2×2×2
7
64
2×2×2×2×2×2
8
128
2×2×2×2×2×2×2
9
256
2×2×···×2
8个2相乘
10
512
2×2×···×2
9个2相乘
64
?
2×2×···×2
63个2相乘
···
···
新知引入
2×2×2×2×2
2+2+2+2+2
=2×5
5个2相加
因数
因数
=10
和
5个2相乘
=25
乘法
乘方
底数
指数
幂
求几个相同的加数的和的运算
求几个相同的因数的积的运算
=32
新知讲解
?
5×5×5×5
?
新知讲解
一般的,任意多个相同的有理数相乘,我们如何去简化表示呢?
?
?
?
?
?
求n个相同因数的积的运算,叫做乘方,乘方的结果叫做幂.
在an中,a叫做底数,
n叫做指数.
?
n个
an
底数
指数
幂
新知讲解
a的n次方
=an
?
跟踪练习
温馨提示:幂的底数是分数或负数时,底数应该添上括号!
2
-5
-5
-5
平方
6
六
六
底数
指数
2.
(-3.4)3,(-3.4)4,(-3.4)5从小到大的顺序是(
)
A.
(-3.4)3<(-3.4)4<(-3.4)5
B.
(-3.4)5<(-3.4)4<(-3.4)3
C.
(-3.4)5<(-3.4)3<(-3.4)4
D.
(-3.4)3<(-3.4)5<(-3.4)4
跟踪练习
C
(-4)2与-42
观察下面两个式子有什么不同?
(-4)2表示-4的平方
-42表示4的平方的相反数
(-4)2与-42
互为相反数.
新知讲解
?
新知应用
?
思考:你发现负数的幂的正负有什么规律?
1.负数的奇次幂是
数,负数的偶次幂是
数.
2.正数的任何次幂都是
数,
的任何正整数次幂都是0.
根据有理数的乘法法则可以得出:
新知讲解
当指数是
数时,负数的幂是
数,
当指数是
数时,负数的幂是
数.
奇
偶
负
正
负
正
正
0
?
新知演练
?
【变式】2.在-|-3|3,-(-3)3,(-3)3,-33中,最大的数是( )
A.-|-3|3
B.-(-3)3
C.(-3)3
D.-33
B
新知演练
是___数
是___数
新知应用
例2
计算:
120=
021=
(-1)9=
.
(-5)3=
(-1)12=
0.13=
.
?
(-5)8
(-16)7
正
负
1
0
-1
-125
1
0.001
?
1
-1
【变式】1.对任意实数a,下列各式不一定成立的是(
)
A.a2=(-a)2
B.
a3=(-a)3
C.|a|=|-a|
D.a2≥0
B
新知演练
2.如果a的倒数是-1,那么a2021等于(
)
A.1
B.-1
C.2021
D.-2021
B
?
新知应用
例3
计算:
(2)-23×(-32)=-8×(-9)=72
(3)64÷(-2)5=64÷(-32)=-2
(4)(-4)3÷(-1)200+2×(-3)4=-64÷1+2×81=98
思考:通过以上计算,对于有理数的乘除和乘方的混合运算,你觉得有怎样的运算顺序?
先算乘方,后算乘除;如果遇到括号就先进行括号里的运算.
新知应用
?
?
?
新知演练
解:(1)0.1×23=0.1×8=0.8(毫米);
(2)0.1×27=0.1×128=12.8(毫米);
(3)0.1×230=0.1×1073741824=107374182.4(毫米).
例4
厚度是0.1毫米的纸,将它对折1次后,厚度为0.2毫米.
(1)对折3次后,厚度为多少毫米?
(2)对折7次后,厚度为多少毫米?
(3)用计算器计算对折30次后纸的厚度.
新知应用
【变式】1.28cm接近于(
)
A.珠穆朗玛峰的高度
B.三层楼的高度
C.姚明的身高
D.一张纸的厚度
新知演练
C
2.某种细菌在培养过程中,没半个小时分裂一次(由一个分裂为两个).若这种细菌由1个分裂成16个,那么这个过程要经过(
)
A.1小时
B.2小时
C.3小时
D.4小时
B
拓展练习
1.计算下列各式:
(-3)1=
;(-3)2=
;(-3)3=
;
(-3)4=
;(-3)5=
.
你发现(-3)n的个位数字有什么规律?
你能用此规律求出(-3)2020的个位数字吗?
-3
9
-27
81
-243
解:
(-3)n的个位数字是4个一循环;
2020÷4=504,
所以(-3)2020的个位数字是1.
拓展练习
2.比较大小:①12
21;②23
32;③34
43;
④45
54;⑤56
65.
猜想:nn+1
(n+1)n(n为整数).
根据你的猜想结论,请比较20202021和20212020的大小.
解:因为12=1,21=2,所以12<21;
因为23=8,32=9,所以23<32;
因为34=81,43=64,所以34>43;
同理45>54,56>65.
拓展练习
2.比较大小:①12
21;②23
32;③34
43;
④45
54;⑤56
65.
猜想:nn+1
(n+1)n(n为整数).
根据你的猜想结论,请比较20202021和20212020的大小.
解:猜想:
当n≤2时,nn+1<(n+1)n
.
当n>2时,nn+1>(n+1)n
.
因为n=2020>2,所以20202021>20212020.
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数;
(2)负数的奇次幂是负数,负数的偶次幂是正数;
(3)零的正整数次幂都是零.
幂
指数
底数
课堂总结
有理数的乘方
从前有个人发明了国际象棋,他的国王知道后很高兴,问他想要什么赏赐,发明国际象棋的人笑了笑,对国王说,大王只要在棋盘的第一个格子放一粒米,以后每格里面都放前面一格两倍的数量,把64个格子放满就可以了.国王听后哈哈大笑,对他说,这个简单,于是命人拿来棋盘,然后开始在棋盘上放米,1粒、2粒、4粒、8粒……,几天过后,国王发现棋盘还没有放满,而自己国家的粮库里已经没有多少米了……
,
国王这才知道自己太小看这个棋盘.
新知引入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
29
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
格
米
算
式
1
1
2
2
3
4
1×2
2×2
4
8
2×2×2
5
16
2×2×2×2
6
32
2×2×2×2×2
7
64
2×2×2×2×2×2
8
128
2×2×2×2×2×2×2
9
256
2×2×···×2
8个2相乘
10
512
2×2×···×2
9个2相乘
64
?
2×2×···×2
63个2相乘
···
···
新知引入
2×2×2×2×2
2+2+2+2+2
=2×5
5个2相加
因数
因数
=10
和
5个2相乘
=25
乘法
乘方
底数
指数
幂
求几个相同的加数的和的运算
求几个相同的因数的积的运算
=32
新知讲解
?
5×5×5×5
?
新知讲解
一般的,任意多个相同的有理数相乘,我们如何去简化表示呢?
?
?
?
?
?
求n个相同因数的积的运算,叫做乘方,乘方的结果叫做幂.
在an中,a叫做底数,
n叫做指数.
?
n个
an
底数
指数
幂
新知讲解
a的n次方
=an
?
跟踪练习
温馨提示:幂的底数是分数或负数时,底数应该添上括号!
2
-5
-5
-5
平方
6
六
六
底数
指数
2.
(-3.4)3,(-3.4)4,(-3.4)5从小到大的顺序是(
)
A.
(-3.4)3<(-3.4)4<(-3.4)5
B.
(-3.4)5<(-3.4)4<(-3.4)3
C.
(-3.4)5<(-3.4)3<(-3.4)4
D.
(-3.4)3<(-3.4)5<(-3.4)4
跟踪练习
C
(-4)2与-42
观察下面两个式子有什么不同?
(-4)2表示-4的平方
-42表示4的平方的相反数
(-4)2与-42
互为相反数.
新知讲解
?
新知应用
?
思考:你发现负数的幂的正负有什么规律?
1.负数的奇次幂是
数,负数的偶次幂是
数.
2.正数的任何次幂都是
数,
的任何正整数次幂都是0.
根据有理数的乘法法则可以得出:
新知讲解
当指数是
数时,负数的幂是
数,
当指数是
数时,负数的幂是
数.
奇
偶
负
正
负
正
正
0
?
新知演练
?
【变式】2.在-|-3|3,-(-3)3,(-3)3,-33中,最大的数是( )
A.-|-3|3
B.-(-3)3
C.(-3)3
D.-33
B
新知演练
是___数
是___数
新知应用
例2
计算:
120=
021=
(-1)9=
.
(-5)3=
(-1)12=
0.13=
.
?
(-5)8
(-16)7
正
负
1
0
-1
-125
1
0.001
?
1
-1
【变式】1.对任意实数a,下列各式不一定成立的是(
)
A.a2=(-a)2
B.
a3=(-a)3
C.|a|=|-a|
D.a2≥0
B
新知演练
2.如果a的倒数是-1,那么a2021等于(
)
A.1
B.-1
C.2021
D.-2021
B
?
新知应用
例3
计算:
(2)-23×(-32)=-8×(-9)=72
(3)64÷(-2)5=64÷(-32)=-2
(4)(-4)3÷(-1)200+2×(-3)4=-64÷1+2×81=98
思考:通过以上计算,对于有理数的乘除和乘方的混合运算,你觉得有怎样的运算顺序?
先算乘方,后算乘除;如果遇到括号就先进行括号里的运算.
新知应用
?
?
?
新知演练
解:(1)0.1×23=0.1×8=0.8(毫米);
(2)0.1×27=0.1×128=12.8(毫米);
(3)0.1×230=0.1×1073741824=107374182.4(毫米).
例4
厚度是0.1毫米的纸,将它对折1次后,厚度为0.2毫米.
(1)对折3次后,厚度为多少毫米?
(2)对折7次后,厚度为多少毫米?
(3)用计算器计算对折30次后纸的厚度.
新知应用
【变式】1.28cm接近于(
)
A.珠穆朗玛峰的高度
B.三层楼的高度
C.姚明的身高
D.一张纸的厚度
新知演练
C
2.某种细菌在培养过程中,没半个小时分裂一次(由一个分裂为两个).若这种细菌由1个分裂成16个,那么这个过程要经过(
)
A.1小时
B.2小时
C.3小时
D.4小时
B
拓展练习
1.计算下列各式:
(-3)1=
;(-3)2=
;(-3)3=
;
(-3)4=
;(-3)5=
.
你发现(-3)n的个位数字有什么规律?
你能用此规律求出(-3)2020的个位数字吗?
-3
9
-27
81
-243
解:
(-3)n的个位数字是4个一循环;
2020÷4=504,
所以(-3)2020的个位数字是1.
拓展练习
2.比较大小:①12
21;②23
32;③34
43;
④45
54;⑤56
65.
猜想:nn+1
(n+1)n(n为整数).
根据你的猜想结论,请比较20202021和20212020的大小.
解:因为12=1,21=2,所以12<21;
因为23=8,32=9,所以23<32;
因为34=81,43=64,所以34>43;
同理45>54,56>65.
拓展练习
2.比较大小:①12
21;②23
32;③34
43;
④45
54;⑤56
65.
猜想:nn+1
(n+1)n(n为整数).
根据你的猜想结论,请比较20202021和20212020的大小.
解:猜想:
当n≤2时,nn+1<(n+1)n
.
当n>2时,nn+1>(n+1)n
.
因为n=2020>2,所以20202021>20212020.
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数;
(2)负数的奇次幂是负数,负数的偶次幂是正数;
(3)零的正整数次幂都是零.
幂
指数
底数
课堂总结
