苏科版数学九年级上册2.4圆周角课件(共19张)
文档属性
| 名称 | 苏科版数学九年级上册2.4圆周角课件(共19张) |  | |
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 21:25:56 | ||
图片预览




文档简介
(共19张PPT)
特征:
①
角的顶点在圆上.
②
角的两边都与圆相交.
顶点在圆上,并且两边都和圆相交的角叫圆周角.
1、圆周角定义:
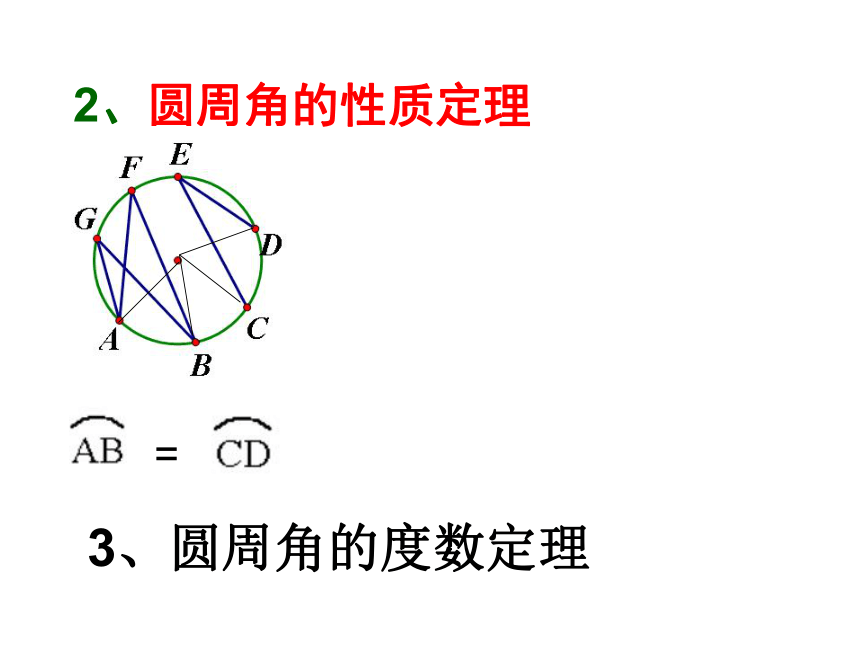
2、圆周角的性质定理
=
3、圆周角的度数定理
1
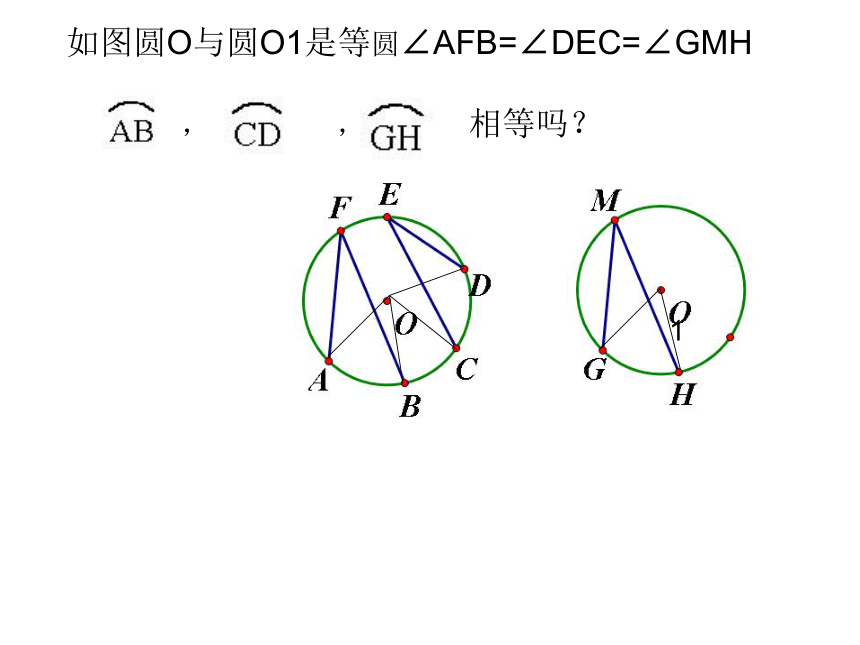
如图圆O与圆O1是等圆∠AFB=∠DEC=∠GMH
,
,
相等吗?
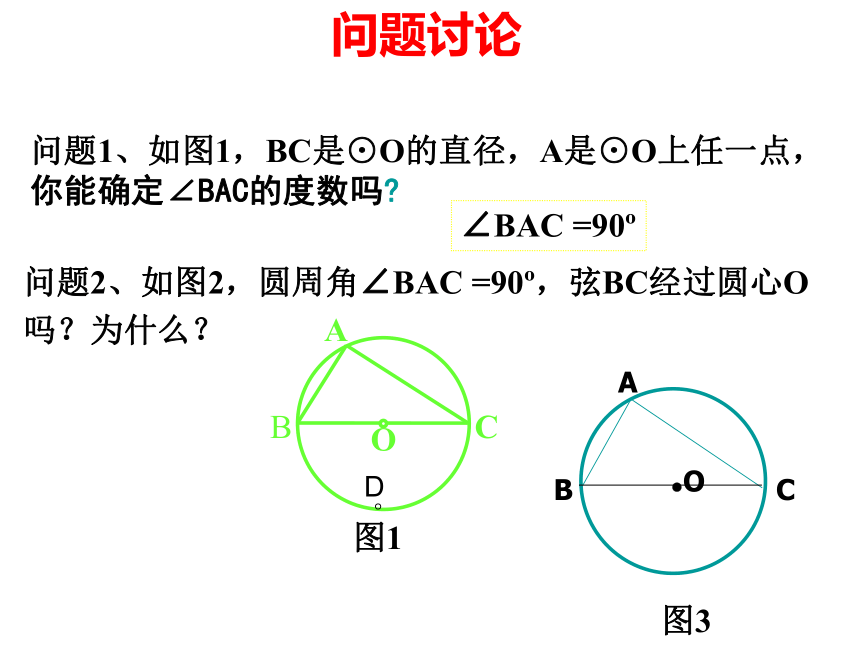
问题讨论
问题1、如图1,BC是⊙O的直径,A是⊙O上任一点,你能确定∠BAC的度数吗?
B
A
O
C
图1
问题2、如图2,圆周角∠BAC
=90?,弦BC经过圆心O吗?为什么?
∠BAC
=90?
●O
B
C
A
图3
。
D
问题解答
1、圆周角定理
同弧或等弧所对的圆周角相等,都等于该弧所对的
圆心角的一半。
3、圆周角定理的推论2:
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。
2、圆周角定理的推论1:
在同圆或等圆中,相等的圆周角所对的弧也相等。
例1.如图,AB为⊙O的直径,弦CD与AB相交于点E,
∠ACD=60°,∠ADC=50°.求∠CEB的度数。
解:连接BD
∵AB是⊙O的直径
∴∠ADB=90°
∵∠ADC=50°
∴∠EDB=∠ADB-∠ADC=90°-50°=40°
∵∠ABD=∠ACD=60°
∴∠CEB=∠B+∠EDB=60°+40°=100°
(直径所对的圆周角是直角)
(同弧所对的圆周角相等)
E
例2
已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
⌒
⌒
求证:
BD=DE
证明:连结AD.
∵AB是圆的直径,点D在圆上,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴AD平分顶角∠BAC,即∠BAD=∠CAD,
∴
⌒
⌒
BD=
DE
(同圆或等圆中,相等的圆周角所对弧相等)。
A
B
C
D
E
例3
一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.
A
B
C
例4
一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.
A
B
C
D
1,已知BC为半圆O的直径,AB=AF,AC交BF于点M,过A点作AD⊥BC于D,交BF于E,则AE与BE的大小有什么关系?为什么?
课堂练习
2.如图,⊙C经过坐标原点O,并与两坐标轴分别交于
A、D两点,已知∠OBA=45°,点D的坐标为(0,2),
求点A的坐标及圆心C的坐标.
E
F
3如图,AB为圆O的直径,OD//BC,OD与
AC与AC交于点E
(1)若∠B=700,求∠CAD的度数
(2)AB=4,AC=3,求DE的长
如图,已知ABC内接于圆O,且AB=AC
直径AD交BC于点E,F是OE上的一点
使CF//BD
(1)求证BE=CE
(2)试判断四边形BFCD形状,
并说明理由
(3)若BC=8,AD=10
,求CD的长
如图,四边形ABCD四个顶点都在圆O上,AC⊥BD,OF⊥AB于F,
求证CD=2OF
G
已知AB是圆O的直径,C是圆周上的动点
P是优弧ABC的中点
(1)如图①求证:OP//BC
(2)如图②,PC交AB于点D,当△ODC
是等腰三角形时,求∠A的度数
H
1、本节课我们学习了哪些知识?
2、圆周角定理及其推论的用途你都知道了吗?
www.czsx.com.cn
作业
驶向胜利的彼岸
再
见
谢谢大家!
特征:
①
角的顶点在圆上.
②
角的两边都与圆相交.
顶点在圆上,并且两边都和圆相交的角叫圆周角.
1、圆周角定义:
2、圆周角的性质定理
=
3、圆周角的度数定理
1
如图圆O与圆O1是等圆∠AFB=∠DEC=∠GMH
,
,
相等吗?
问题讨论
问题1、如图1,BC是⊙O的直径,A是⊙O上任一点,你能确定∠BAC的度数吗?
B
A
O
C
图1
问题2、如图2,圆周角∠BAC
=90?,弦BC经过圆心O吗?为什么?
∠BAC
=90?
●O
B
C
A
图3
。
D
问题解答
1、圆周角定理
同弧或等弧所对的圆周角相等,都等于该弧所对的
圆心角的一半。
3、圆周角定理的推论2:
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。
2、圆周角定理的推论1:
在同圆或等圆中,相等的圆周角所对的弧也相等。
例1.如图,AB为⊙O的直径,弦CD与AB相交于点E,
∠ACD=60°,∠ADC=50°.求∠CEB的度数。
解:连接BD
∵AB是⊙O的直径
∴∠ADB=90°
∵∠ADC=50°
∴∠EDB=∠ADB-∠ADC=90°-50°=40°
∵∠ABD=∠ACD=60°
∴∠CEB=∠B+∠EDB=60°+40°=100°
(直径所对的圆周角是直角)
(同弧所对的圆周角相等)
E
例2
已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
⌒
⌒
求证:
BD=DE
证明:连结AD.
∵AB是圆的直径,点D在圆上,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴AD平分顶角∠BAC,即∠BAD=∠CAD,
∴
⌒
⌒
BD=
DE
(同圆或等圆中,相等的圆周角所对弧相等)。
A
B
C
D
E
例3
一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.
A
B
C
例4
一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.
A
B
C
D
1,已知BC为半圆O的直径,AB=AF,AC交BF于点M,过A点作AD⊥BC于D,交BF于E,则AE与BE的大小有什么关系?为什么?
课堂练习
2.如图,⊙C经过坐标原点O,并与两坐标轴分别交于
A、D两点,已知∠OBA=45°,点D的坐标为(0,2),
求点A的坐标及圆心C的坐标.
E
F
3如图,AB为圆O的直径,OD//BC,OD与
AC与AC交于点E
(1)若∠B=700,求∠CAD的度数
(2)AB=4,AC=3,求DE的长
如图,已知ABC内接于圆O,且AB=AC
直径AD交BC于点E,F是OE上的一点
使CF//BD
(1)求证BE=CE
(2)试判断四边形BFCD形状,
并说明理由
(3)若BC=8,AD=10
,求CD的长
如图,四边形ABCD四个顶点都在圆O上,AC⊥BD,OF⊥AB于F,
求证CD=2OF
G
已知AB是圆O的直径,C是圆周上的动点
P是优弧ABC的中点
(1)如图①求证:OP//BC
(2)如图②,PC交AB于点D,当△ODC
是等腰三角形时,求∠A的度数
H
1、本节课我们学习了哪些知识?
2、圆周角定理及其推论的用途你都知道了吗?
www.czsx.com.cn
作业
驶向胜利的彼岸
再
见
谢谢大家!
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
